Podobnie jak bagging i boosting, boosting gradientowy to metoda stosowana na podstawie innego algorytmu systemów uczących się. Ulepszanie gradientem to nieformalnie dwa typy modeli:
- „słaby” model uczenia maszynowego, który zwykle jest drzewem decyzyjnym;
- „mocny” model uczenia maszynowego, który składa się z wielu słabych modeli;
W każdej iteracji wzmacniania gradientowego nowy słaby model jest trenowany w celu przewidywania „błędu” obecnego silnego modelu (nazywanego pseudoodpowiedzią). Szczegóły dotyczące „błędu” podamy później. Przyjmijmy na razie, że „błąd” to różnica między prognozą a etykietą regresji. Słabszy model (czyli „błąd”) jest następnie dodawany do mocniejszego modelu z ujemnym znakiem, aby zmniejszyć błąd mocniejszego modelu.
Wzmocnienie gradientowe jest procesem iteracyjnym. Każda iteracja wywołuje tę formułę:
\[ F_{i+1} = F_i - f_i \]
gdzie:
- $F_i$ to silny model na kroku i.
- $f_i$ to słaby model na kroku $i$.
Ta operacja jest powtarzana, dopóki nie zostanie spełnione kryterium zatrzymania, np. maksymalna liczba iteracji lub gdy model (silny) zacznie się nadmiernie dopasowywać do danych, co można zmierzyć na osobnym zbiorze danych do walidacji.
Zastosujmy wzmacnianie gradientu na prostym zbiorze danych regresji, w którym:
- Celem jest prognozowanie wartości y na podstawie wartości x.
- Model silny jest inicjowany jako stała zerowa: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Zastosujmy ten kod do tego zbioru danych:
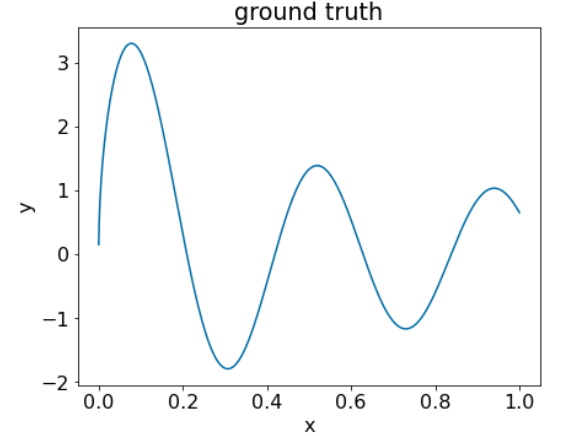
Rysunek 25. Syntetyczny regresyjny zbiór danych z 1 charakterystyką liczbową.
Oto 3 wykresy po pierwszej iteracji algorytmu gradient boosting:
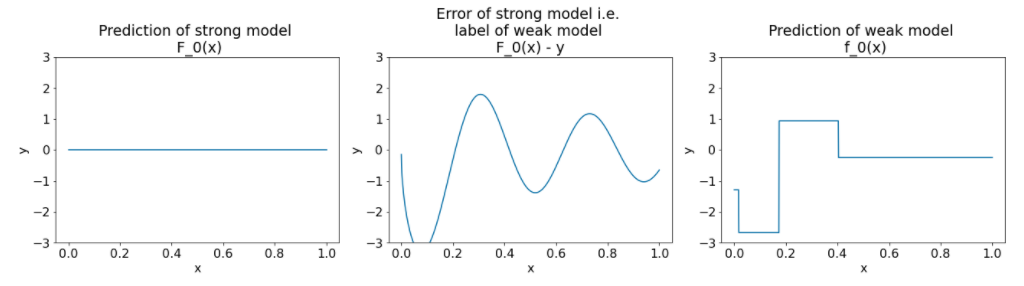
Rysunek 26. Trzy wykresy po pierwszej iteracji.
Na wykresach na rysunku 26 zwróć uwagę na te kwestie:
- Pierwszy wykres przedstawia prognozy modelu silnego, który jest obecnie zawsze równy 0.
- Drugi wykres pokazuje błąd, czyli etykietę słabego modelu.
- Trzeci wykres pokazuje słaby model.
Pierwszy słaby model uczy się ogólnego przedstawienia etykiety i skupia się głównie na lewej części przestrzeni cech (części o największej zmienności, a zatem o największym błędzie w przypadku nieprawidłowego modelu stałego).
Poniżej znajdują się te same wykresy dla innej iteracji algorytmu:
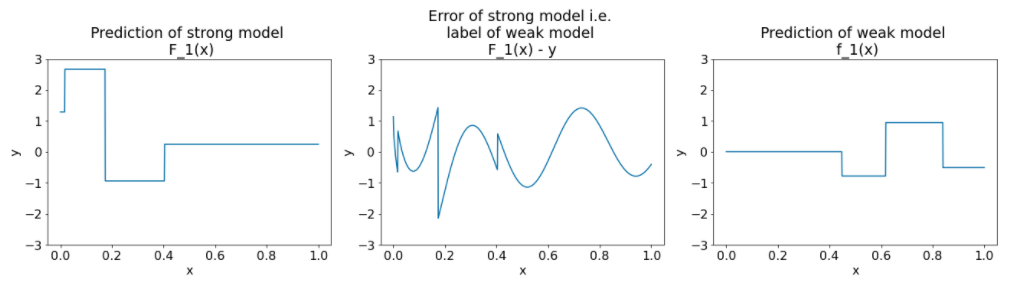
Rysunek 27. 3 wykresy po 2 iteracjach.
Zwróć uwagę na te informacje dotyczące wykresów na rysunku 27:
- Model silny zawiera teraz prognozę modelu słabego z poprzedniej iteracji.
- Nowy błąd modelu silnego jest nieco mniejszy.
- Nowa prognoza słabego modelu koncentruje się teraz na prawej części przestrzeni cech.
Algorytm wykonuje 8 kolejnych iteracji:
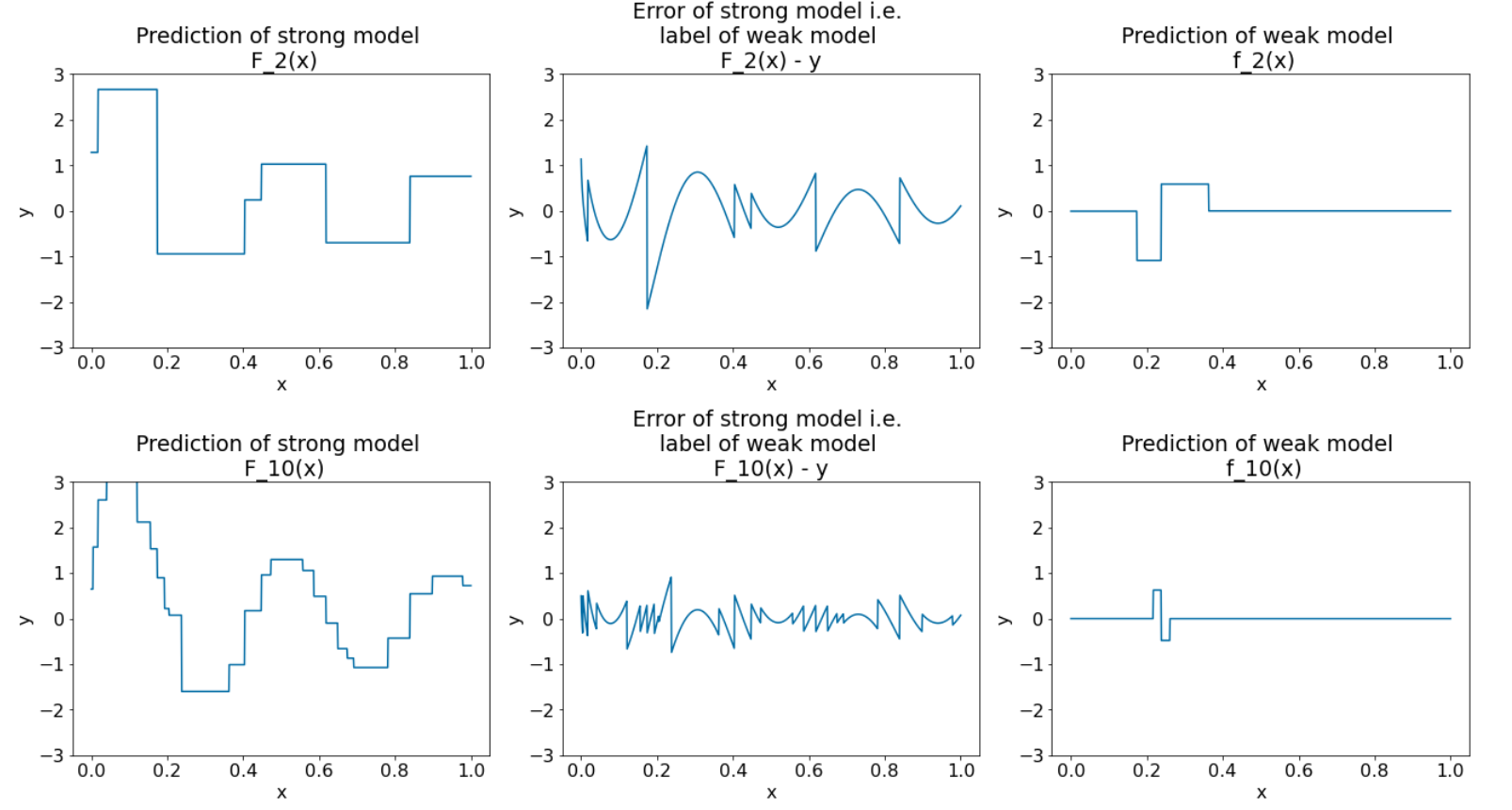
Rysunek 28. 3 wykresy po 3 i 10 iteracjach.
Na rysunku 28 widać, że prognoza uzyskana przez silny model zaczyna przypominać wykres zbioru danych.
Rysunki te przedstawiają algorytm gradient boosting, który wykorzystuje drzewa decyzyjne jako słabe modele. Ta kombinacja nosi nazwę drzewa decyzyjnego z wzmocnieniem gradientowym.
Poprzednie wykresy przedstawiają istotę gradient boostingu. W tym przykładzie brakuje jednak tych 2 operacji z rzeczywistego świata:
- kurczenie się
- Optymalizacja wartości liści za pomocą jednego kroku metody Newtona
Skurcz
Model słaby $f_i$ jest mnożony przez małą wartość $\nu$ (np. $\nu = 0.1$), zanim zostanie dodany do modelu silnego $F_i$. Ta mała wartość jest nazywana kurczeniem. Inaczej mówiąc, zamiast każdej iteracji za pomocą tej formuły:
\[ F_{i+1} = F_i - f_i \]
Każda iteracja używa tej formuły:
\[ F_{i+1} = F_i - \nu f_i \]
Kurczenie się w boostingu gradientowym jest analogiczne do szybkości uczenia się w sieciach neuronowych. Skurcz kontroluje szybkość uczenia się silnego modelu, co pomaga ograniczyć nadmierne dopasowanie. Oznacza to, że wartość skurczenia bliska 0,0 zmniejsza przeuczenie bardziej niż wartość skurczenia bliska 1,0.
W powyższym kodzie zwiotczenie zostałoby zaimplementowane w ten sposób:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
