बैगिंग और बूसटिंग की तरह, ग्रेडिएंट बूसटिंग भी एक ऐसा तरीका है जिसे किसी दूसरे मशीन लर्निंग एल्गोरिदम के ऊपर लागू किया जाता है. आम तौर पर, ग्रेडिएंट बूसटिंग में दो तरह के मॉडल शामिल होते हैं:
- "कमज़ोर" मशीन लर्निंग मॉडल, जो आम तौर पर डिसीज़न ट्री होता है.
- एक "बेहतर" मशीन लर्निंग मॉडल, जो कई कमज़ोर मॉडल से बना होता है.
ग्रेडिएंट बूस्टिंग में, हर चरण में एक नए कमज़ोर मॉडल को ट्रेनिंग दी जाती है, ताकि मौजूदा बेहतर मॉडल की "गड़बड़ी" का अनुमान लगाया जा सके. इसे स्यूडो रिस्पॉन्स कहा जाता है. हम "गड़बड़ी" के बारे में बाद में बताएंगे. फ़िलहाल, मान लें कि "गड़बड़ी", अनुमान और रिग्रेसिव लेबल के बीच का अंतर है. इसके बाद, खराब मॉडल (यानी "गड़बड़ी") को नेगेटिव साइन के साथ बेहतर मॉडल में जोड़ा जाता है, ताकि बेहतर मॉडल की गड़बड़ी को कम किया जा सके.
ग्रेडिएंट बूस्टिंग, बार-बार इस्तेमाल होने वाली प्रोसेस है. हर बार यह फ़ॉर्मूला लागू होता है:
\[ F_{i+1} = F_i - f_i \]
कहां:
- $F_i$, चरण $i$ में बेहतर मॉडल है.
- $f_i$, चरण $i$ में मौजूद खराब मॉडल है.
यह कार्रवाई तब तक दोहराई जाती है, जब तक कि रोकने की शर्त पूरी नहीं हो जाती. जैसे, दोहराए जाने की ज़्यादा से ज़्यादा संख्या या अगर (मज़बूत) मॉडल, पुष्टि करने वाले अलग डेटासेट पर मेज़र किए गए ओवरफ़िट होने लगता है.
आइए, एक सिंपल रिग्रेशन डेटासेट पर ग्रेडिएंट बूसटिंग के बारे में बताते हैं, जहां:
- इसका मकसद, $x$ से $y$ का अनुमान लगाना है.
- स्ट्रॉन्ग मॉडल को शून्य कॉन्स्टेंट के तौर पर शुरू किया जाता है: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
आइए, इस कोड को नीचे दिए गए डेटासेट पर लागू करें:
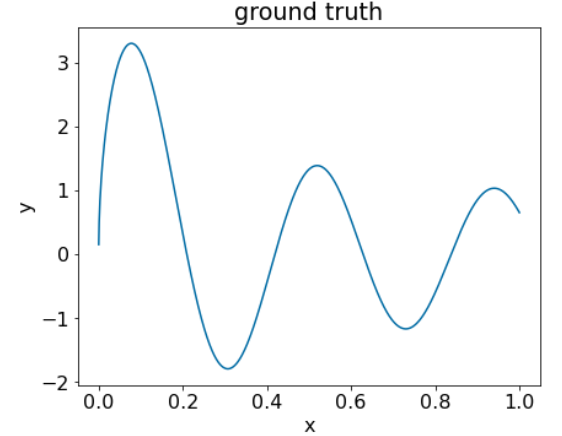
25वां चित्र. एक संख्या वाली सुविधा वाला सिंथेटिक रिग्रेशन डेटासेट.
ग्रेडिएंट बूसटिंग एल्गोरिदम के पहले दोहराव के बाद, यहां तीन प्लॉट दिए गए हैं:
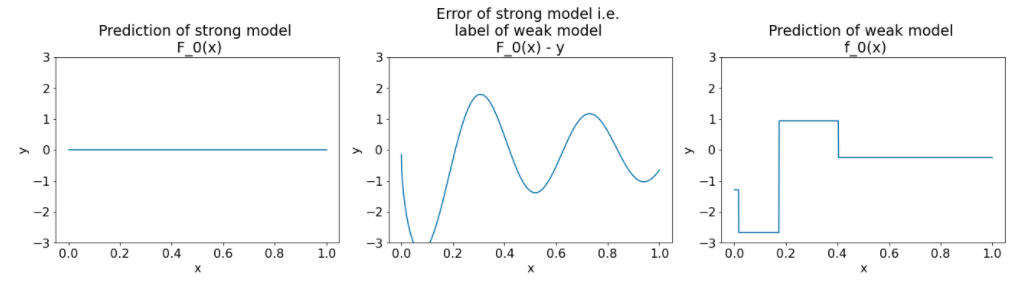
26वां चित्र. पहले दोहराए जाने के बाद तीन प्लॉट.
इमेज 26 में दिए गए प्लॉट के बारे में इन बातों का ध्यान रखें:
- पहला प्लॉट, बेहतर मॉडल के अनुमान दिखाता है. फ़िलहाल, यह हमेशा 0 होता है.
- दूसरा प्लॉट, गड़बड़ी दिखाता है. यह गड़बड़ी, खराब मॉडल का लेबल होता है.
- तीसरा प्लॉट, खराब मॉडल दिखाता है.
पहला खराब मॉडल, लेबल के बारे में कम जानकारी वाला डेटा सीख रहा है. यह ज़्यादातर, फ़ीचर स्पेस के बाएं हिस्से पर फ़ोकस करता है. यह वह हिस्सा होता है जिसमें सबसे ज़्यादा वैरिएशन होता है. इसलिए, लगातार गलत मॉडल के लिए सबसे ज़्यादा गड़बड़ी होती है.
एल्गोरिदम के दूसरे आइटरेशन के लिए, ये वही प्लॉट हैं:
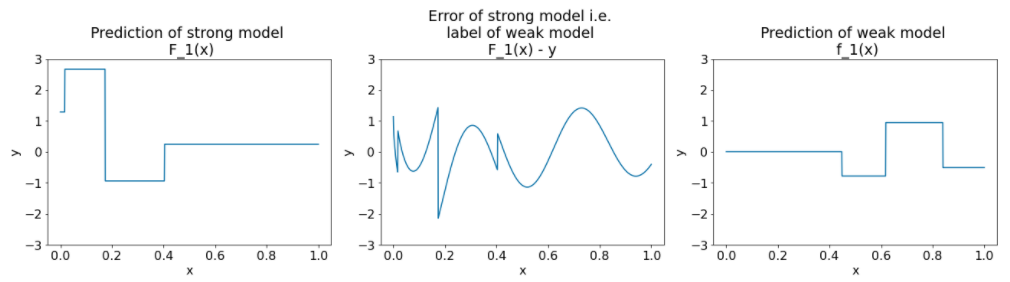
27वीं इमेज. दूसरे दोहराव के बाद तीन प्लॉट.
इमेज 27 में दिए गए प्लॉट के बारे में इन बातों का ध्यान रखें:
- बेहतर मॉडल में अब पिछले इंटेशन के कमज़ोर मॉडल का अनुमान शामिल है.
- बेहतर मॉडल की नई गड़बड़ी थोड़ी कम है.
- खराब मॉडल का नया अनुमान, अब फ़ीचर स्पेस के दाएं हिस्से पर फ़ोकस करता है.
हम एल्गोरिदम को आठ और बार चलाते हैं:
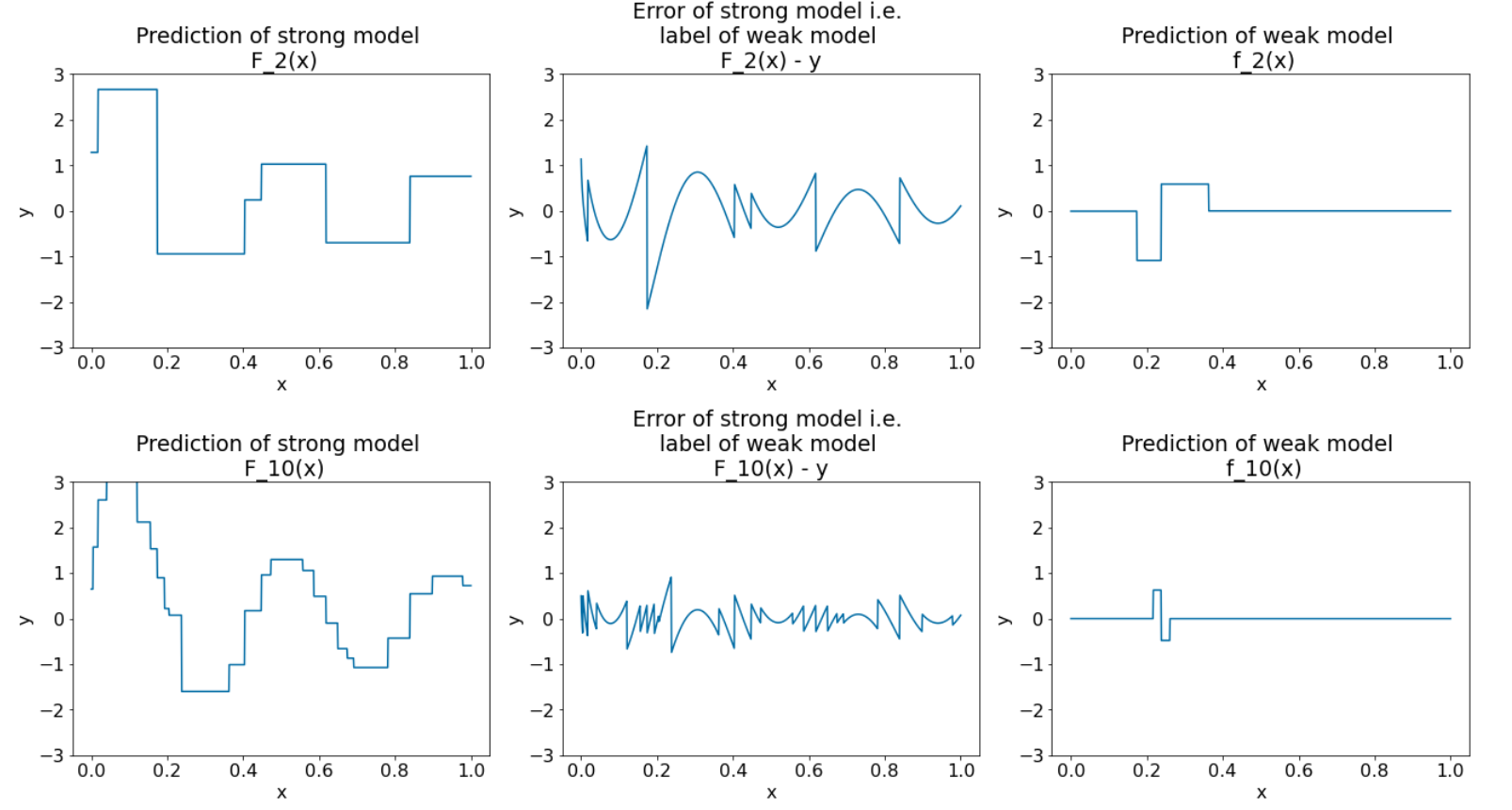
28वां चित्र. तीसरे और दसवें दोहराव के बाद तीन प्लॉट.
इमेज 28 में, ध्यान दें कि बेहतर मॉडल का अनुमान, डेटासेट के प्लॉट से मिलता-जुलता है.
इन आंकड़ों में, कम परफ़ॉर्म करने वाले लर्नर के तौर पर, डिसीज़न ट्री का इस्तेमाल करने वाले ग्रेडिएंट बूसटिंग एल्गोरिदम को दिखाया गया है. इस कॉम्बिनेशन को ग्रेडिएंट बूस्ड (फ़ैसला लेने वाले) ट्री कहा जाता है.
ऊपर दिए गए प्लॉट से, ग्रेडिएंट बूसटिंग के बारे में पता चलता है. हालांकि, इस उदाहरण में असल दुनिया के ये दो काम नहीं किए गए हैं:
- वीडियो का छोटा होना
- न्यूटन के तरीके के एक चरण की मदद से, लीफ़ वैल्यू को ऑप्टिमाइज़ करना
सिकुड़ना
बेहतर मॉडल $F_i$ में जोड़े जाने से पहले, कम मॉडल $f_i$ को एक छोटी वैल्यू $\nu$ (उदाहरण के लिए, $\nu = 0.1$) से गुणा किया जाता है. इस छोटी वैल्यू को छोटा करना कहा जाता है. दूसरे शब्दों में, हर बार नीचे दिए गए फ़ॉर्मूला का इस्तेमाल करने के बजाय:
\[ F_{i+1} = F_i - f_i \]
हर बार, इस फ़ॉर्मूला का इस्तेमाल किया जाता है:
\[ F_{i+1} = F_i - \nu f_i \]
ग्रेडिएंट बूसटिंग में शंर्केज, न्यूरल नेटवर्क में लर्निंग रेट जैसा ही है. शंर्केज से यह कंट्रोल होता है कि बेहतर मॉडल कितनी तेज़ी से सीख रहा है. इससे, ओवरफ़िटिंग को सीमित करने में मदद मिलती है. इसका मतलब है कि शंकु के आकार में होने वाली कमी की वैल्यू 0.0 के करीब होने पर, 1.0 के करीब होने वाली वैल्यू की तुलना में, ओवरफ़िटिंग कम होती है.
ऊपर दिए गए कोड में, डेटा को छोटा करने की प्रोसेस इस तरह से लागू होगी:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
