Gradient Boosted-Entscheidungsbäume

Ähnlich wie Bagging und Boosting ist Gradient Boosting eine Methode, die auf einem anderen Algorithmus für maschinelles Lernen angewendet wird. Im Allgemeinen umfasst Gradient Boosting zwei Arten von Modellen:

• ein „schwaches“ Modell für maschinelles Lernen, in der Regel ein Entscheidungsbaum.
• ein „starkes“ Machine-Learning-Modell, das aus mehreren schwachen Modellen besteht.

Bei der Gradienten-Optimierung wird in jedem Schritt ein neues schwaches Modell trainiert, um den „Fehler“ des aktuellen starken Modells vorherzusagen (dies wird als Pseudoantwort bezeichnet). „Fehler“ wird später erläutert. Angenommen, „Fehler“ ist die Differenz zwischen der Vorhersage und einem regressiven Label. Das schwache Modell (d. h. der „Fehler“) wird dann dem starken Modell mit einem negativen Vorzeichen hinzugefügt, um den Fehler des starken Modells zu reduzieren.

Die Gradientenverstärkung ist iterativ. Bei jeder Iteration wird die folgende Formel aufgerufen:

\[ F_{i+1} = F_i - f_i \]

Dabei gilt:

• $F_i$ ist das starke Modell in Schritt i.
• $f_i$ ist das schwache Modell in Schritt i.

Dieser Vorgang wird wiederholt, bis ein Stopp-Kriterium erfüllt ist, z. B. eine maximale Anzahl von Iterationen oder wenn das (starke) Modell beginnt, sich an die Daten anzupassen, wie in einem separaten Validierungsdatensatz gemessen.

Sehen wir uns Gradient Boosting anhand eines einfachen Regressionsdatensatzes an, bei dem:

• Ziel ist es, y anhand von x vorherzusagen.
• Das starke Modell wird mit einer Nullkonstanten initialisiert: $F_0(x) = 0$.

Hinweis: Der folgende Code dient nur zu Bildungszwecken. In der Praxis rufen Sie einfach tfdf.keras.GradientBoostedTreeModel auf.

# Simplified example of regressive gradient boosting.

y = ... # the labels
x = ... # the features

strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.

for i in range(num_iters):

    # Error of the strong model
    error = strong_predictions - y

    # The weak model is a decision tree (see CART chapter)
    # without pruning and a maximum depth of 3.
    weak_model = tfdf.keras.CartModel(
        task=tfdf.keras.Task.REGRESSION,
        validation_ratio=0.0,
        max_depth=3)
    weak_model.fit(x=x, y=error)

    strong_model.append(weak_model)

    weak_predictions = weak_model.predict(x)[:,0]

    strong_predictions -= weak_predictions

Wenden wir diesen Code auf den folgenden Datensatz an:

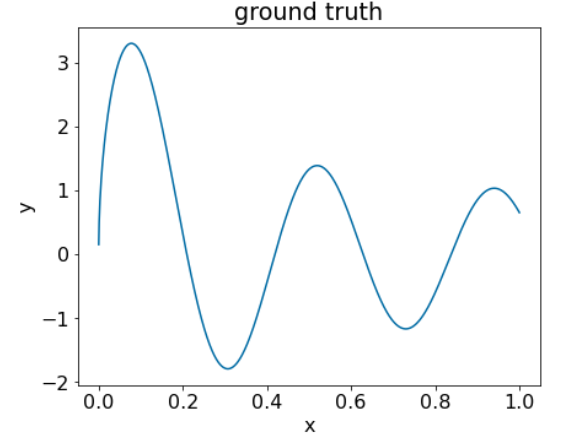
Abbildung 25. Ein synthetischer regressiver Datensatz mit einer numerischen Funktion.

 

Hier sind drei Diagramme nach der ersten Iteration des Gradient Boosting-Algorithmus:

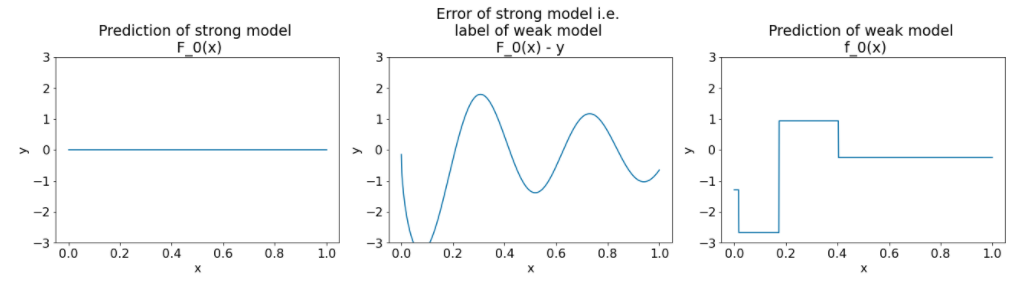
Abbildung 26. Drei Diagramme nach der ersten Iteration.

 

Beachten Sie bei den Plots in Abbildung 26 Folgendes:

• Das erste Diagramm zeigt die Vorhersagen des leistungsstarken Modells, das derzeit immer 0 ist.
• Das zweite Diagramm zeigt den Fehler, also das Label des schwachen Modells.
• Das dritte Diagramm zeigt das schwache Modell.

Das erste schwache Modell lernt eine grobe Darstellung des Labels und konzentriert sich hauptsächlich auf den linken Teil des Feature-Spaces (den Teil mit der größten Variation und daher den meisten Fehlern für das konstant falsche Modell).

Unten sehen Sie dieselben Diagramme für eine andere Iteration des Algorithmus:

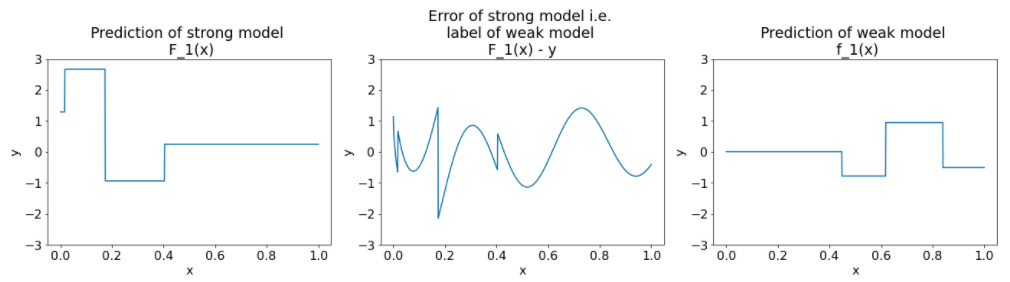
Abbildung 27. Drei Diagramme nach der zweiten Iteration.

 

Beachten Sie Folgendes zu den Plots in Abbildung 27:

• Das starke Modell enthält jetzt die Vorhersage des schwachen Modells der vorherigen Iteration.
• Der neue Fehler des starken Modells ist etwas kleiner.
• Die neue Vorhersage des schwachen Modells konzentriert sich jetzt auf den rechten Teil des Feature-Spaces.

Wir führen den Algorithmus noch achtmal aus:

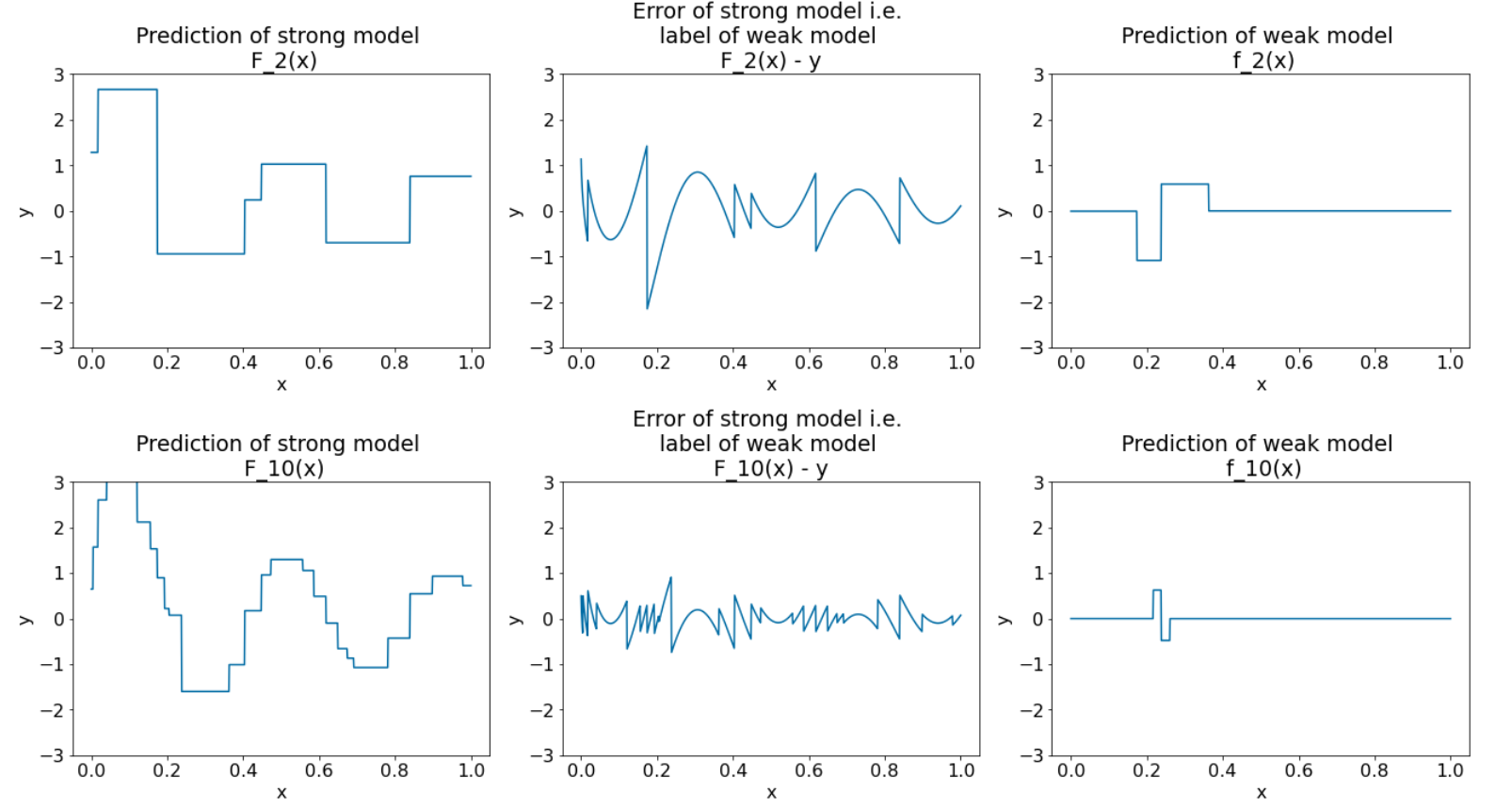
Abbildung 28. Drei Diagramme nach der dritten und der zehnten Iteration.

 

In Abbildung 28 sehen Sie, dass die Vorhersage des starken Modells der Darstellung des Datensatzes ähnelt.

Diese Abbildungen veranschaulichen den Gradienten-Boosting-Algorithmus mit Entscheidungsbäumen als schwache Lernenden. Diese Kombination wird als Gradient Boosted (Entscheidungs)Trees bezeichnet.

Die vorherigen Grafiken veranschaulichen das Wesen von Gradient Boosting. In diesem Beispiel fehlen jedoch die folgenden beiden realen Vorgänge:

• Die Schrumpfung
• Optimierung von Blattwerten mit einem Schritt der Newton-Methode

Hinweis: In der Praxis gibt es mehrere Varianten des Gradient Boosting-Algorithmus mit anderen Vorgängen.

Schrumpfung

Das schwache Modell f_i wird mit einem kleinen Wert ν multipliziert (z. B. ν = 0,1), bevor es dem starken Modell F_i hinzugefügt wird. Dieser kleine Wert wird als Schrumpfung bezeichnet. Anders ausgedrückt: Anstatt für jede Iteration die folgende Formel zu verwenden:

\[ F_{i+1} = F_i - f_i \]

Für jede Iteration wird die folgende Formel verwendet:

\[ F_{i+1} = F_i - \nu f_i \]

Die Schrumpfung bei der Gradientenverstärkung entspricht der Lernrate bei neuronalen Netzwerken. Mit der Schrumpfung wird gesteuert, wie schnell das starke Modell lernt. So lässt sich Überanpassung besser vermeiden. Mit einem Schrumpfungsfaktor, der näher an 0,0 liegt, wird das Überanpassen stärker reduziert als mit einem Schrumpfungsfaktor, der näher an 1,0 liegt.

In unserem Code oben würde die Schrumpfung so implementiert:

shrinkage = 0.1   # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions