Comme le bagging et le boosting, le boosting de gradient est une méthodologie appliquée sur un autre algorithme de machine learning. De manière informelle, le boosting par gradient implique deux types de modèles:
- un modèle de machine learning "faible", qui est généralement un arbre de décision.
- un modèle de machine learning "fort", qui est composé de plusieurs modèles faibles.
Dans le boosting par gradient, à chaque étape, un nouveau modèle faible est entraîné pour prédire l'"erreur" du modèle fort actuel (appelé pseudo-réponse). Nous reviendrons sur le terme "erreur" plus tard. Pour l'instant, supposons que l'erreur corresponde à la différence entre la prédiction et un libellé régressif. Le modèle faible (c'est-à-dire l'"erreur") est ensuite ajouté au modèle fort avec un signe négatif pour réduire l'erreur du modèle fort.
L'optimisation de gradient est un processus itératif. Chaque itération appelle la formule suivante:
\[ F_{i+1} = F_i - f_i \]
où :
- $F_i$ est le modèle performant à l'étape i.
- $f_i$ est le modèle faible à l'étape i.
Cette opération se répète jusqu'à ce qu'un critère d'arrêt soit atteint, comme un nombre maximal d'itérations ou si le modèle (fort) commence à surajuster, mesuré sur un ensemble de données de validation distinct.
Illustrons le renforcement par gradient sur un ensemble de données de régression simple où:
- L'objectif est de prédire $y$ à partir de $x$.
- Le modèle fort est initialisé avec une constante nulle: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Appliquez ce code à l'ensemble de données suivant:
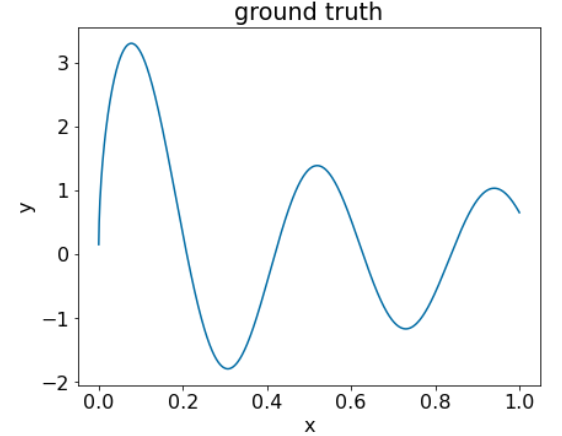
Figure 25. Ensemble de données régressif synthétique avec une caractéristique numérique.
Voici trois graphiques après la première itération de l'algorithme de boosting du gradient:
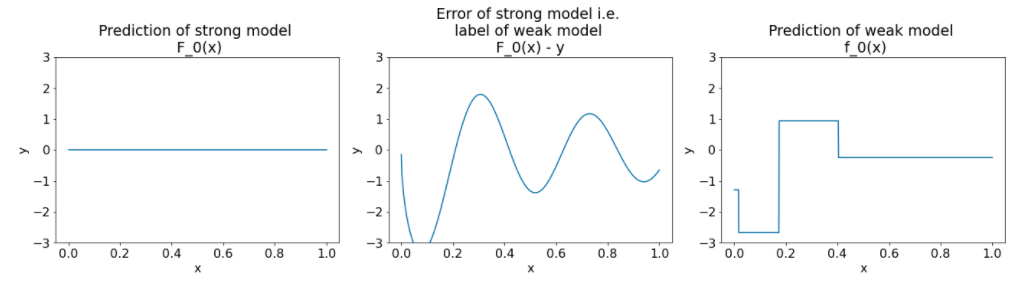
Figure 26. Trois graphiques après la première itération.
Notez les points suivants concernant les graphiques de la figure 26:
- Le premier graphique montre les prédictions du modèle fort, qui est actuellement toujours égal à 0.
- Le deuxième graphique montre l'erreur, qui correspond à l'étiquette du modèle faible.
- Le troisième graphique montre le modèle faible.
Le premier modèle faible apprend une représentation approximative du libellé et se concentre principalement sur la partie gauche de l'espace des caractéristiques (la partie présentant la plus grande variation et donc la plus grande erreur pour le modèle incorrect constant).
Vous trouverez ci-dessous les mêmes graphiques pour une autre itération de l'algorithme:
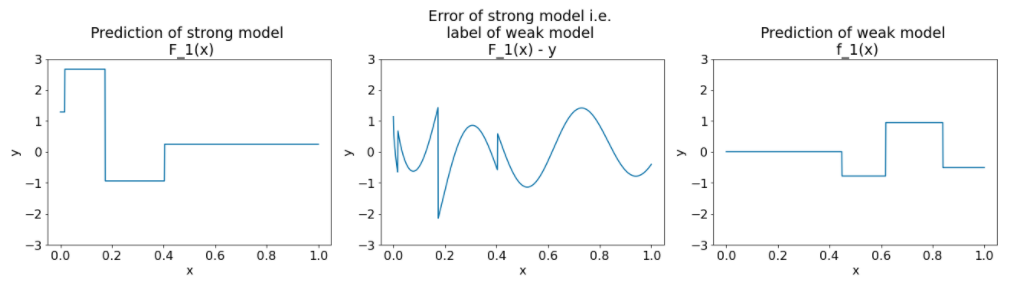
Figure 27. Trois graphiques après la deuxième itération.
Notez les points suivants concernant les graphiques de la figure 27:
- Le modèle fort contient désormais la prédiction du modèle faible de l'itération précédente.
- La nouvelle erreur du modèle fort est un peu plus faible.
- La nouvelle prédiction du modèle faible se concentre désormais sur la partie droite de l'espace des caractéristiques.
Nous exécutons l'algorithme pendant huit autres itérations:
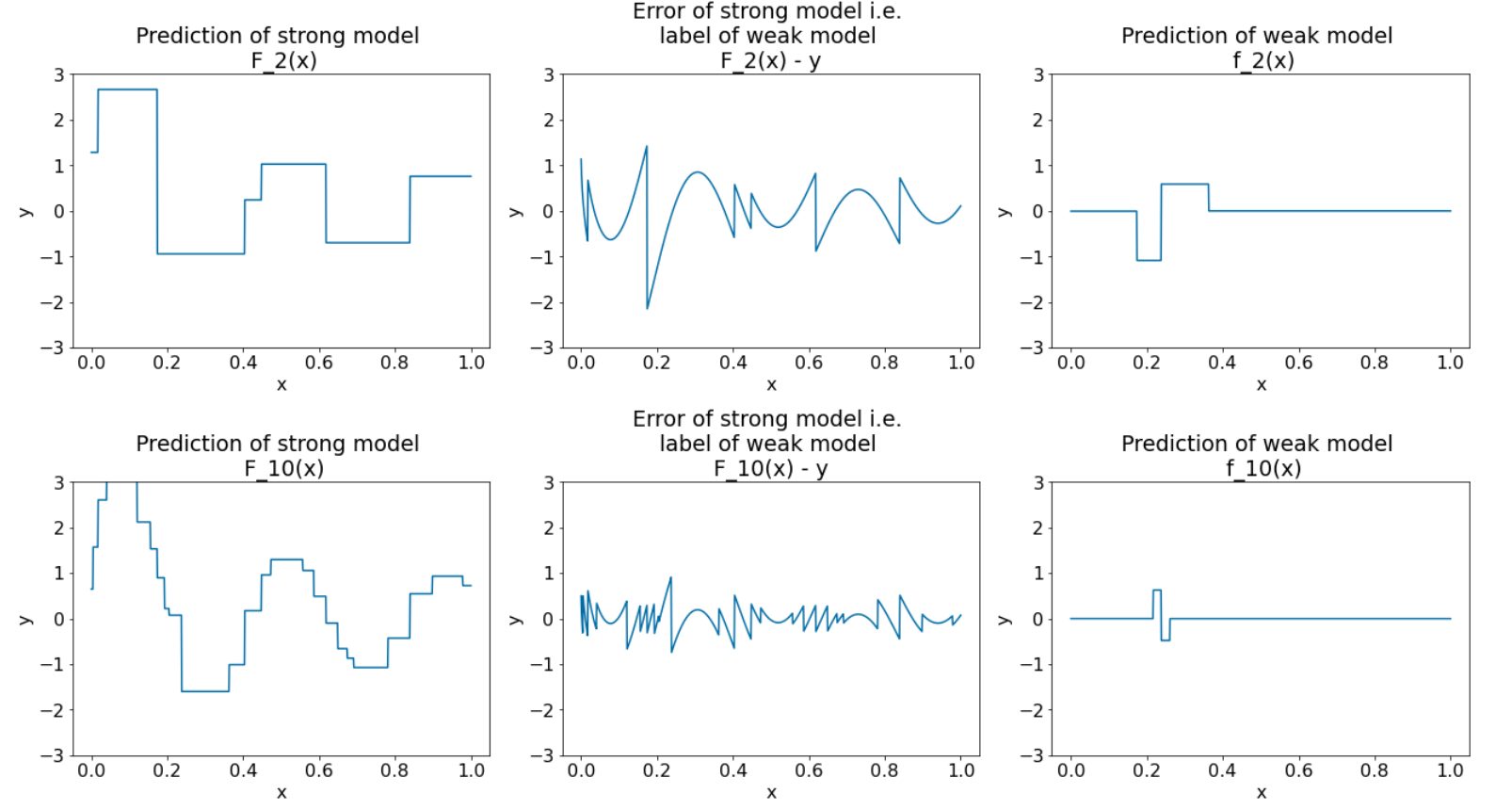
Figure 28. Trois graphiques après la troisième itération et la dixième itération.
Dans la figure 28, notez que la prédiction du modèle performant commence à ressembler à la courbe de l'ensemble de données.
Ces figures illustrent l'algorithme de boosting de gradient utilisant des arbres de décision comme apprenants faibles. Cette combinaison est appelée arbres de décision à boosting de gradient.
Les graphiques précédents suggèrent l'essence du boosting par gradient. Toutefois, cet exemple ne comporte pas les deux opérations réelles suivantes:
- Le rétrécissement
- Optimisation des valeurs des feuilles avec une étape de la méthode de Newton
Rétrécissement
Le modèle faible $f_i$ est multiplié par une petite valeur $\nu$ (par exemple, $\nu = 0,1$) avant d'être ajouté au modèle fort $F_i$. Cette petite valeur est appelée rétrécissement. En d'autres termes, au lieu de chaque itération utilisant la formule suivante:
\[ F_{i+1} = F_i - f_i \]
Chaque itération utilise la formule suivante:
\[ F_{i+1} = F_i - \nu f_i \]
Le rétrécissement dans le boosting par gradient est analogue au taux d'apprentissage dans les réseaux de neurones. Le rétrécissement contrôle la vitesse d'apprentissage du modèle fort, ce qui permet de limiter le surajustement. Autrement dit, une valeur de rétrécissement plus proche de 0,0 réduit davantage le surajustement qu'une valeur de rétrécissement plus proche de 1,0.
Dans notre code ci-dessus, le rétrécissement serait implémenté comme suit:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
