ต้นไม้การตัดสินใจที่เพิ่มระดับการไล่ระดับสี

เช่นเดียวกับการแบ่งกลุ่มและการเพิ่มประสิทธิภาพ การเพิ่มความชันเป็นวิธีการที่ใช้ร่วมกับอัลกอริทึมแมชชีนเลิร์นนิงอื่น การเพิ่มประสิทธิภาพด้วย Gradient เกี่ยวข้องกับโมเดล 2 ประเภท ได้แก่

• โมเดลแมชชีนเลิร์นนิงที่ "อ่อน" ซึ่งโดยทั่วไปคือแผนภูมิการตัดสินใจ
• โมเดลแมชชีนเลิร์นนิงที่ "มีประสิทธิภาพ" ซึ่งประกอบด้วยโมเดลที่มีประสิทธิภาพต่ำหลายโมเดล

ในการเพิ่มประสิทธิภาพด้วย Gradient Boosting แต่ละขั้นตอนจะมีการฝึกโมเดลที่มีประสิทธิภาพต่ำแบบใหม่เพื่อคาดการณ์ "ข้อผิดพลาด" ของโมเดลที่มีประสิทธิภาพสูงปัจจุบัน (ซึ่งเรียกว่าการตอบสนองจำลอง) เราจะอธิบายรายละเอียด "error" ในภายหลัง ในระหว่างนี้ ให้ถือว่า "ข้อผิดพลาด" คือความแตกต่างระหว่างการคาดการณ์กับป้ายกำกับแบบถดถอย จากนั้นจะเพิ่มโมเดลที่มีประสิทธิภาพต่ำ (นั่นคือ "ข้อผิดพลาด") ลงในโมเดลที่มีประสิทธิภาพสูงโดยใส่เครื่องหมายลบเพื่อลดข้อผิดพลาดของโมเดลที่มีประสิทธิภาพสูง

การบูสต์ด้วย Gradient เป็นกระบวนการที่ต้องทำซ้ำ แต่ละรอบจะเรียกใช้สูตรต่อไปนี้

\[ F_{i+1} = F_i - f_i \]

where:

• $F_i$ คือโมเดลที่มีประสิทธิภาพในระยะ $i$
• $f_i$ คือโมเดลที่มีประสิทธิภาพต่ำในขั้นตอน $i$

การดำเนินการนี้จะซ้ำไปจนกว่าจะเป็นไปตามเกณฑ์การหยุด เช่น จํานวนการวนซ้ำสูงสุด หรือหากโมเดล (ที่มีประสิทธิภาพสูง) เริ่มปรับให้พอดีมากเกินไปตามที่วัดในชุดข้อมูลที่ใช้ตรวจสอบแยกต่างหาก

มาดูตัวอย่างการเพิ่มประสิทธิภาพด้วย Gradient Boosting ในชุดข้อมูลการหาค่าประมาณแบบง่ายกัน ดังนี้

• วัตถุประสงค์คือคาดการณ์ $y$ จาก $x$
• ระบบจะเริ่มต้นค่าประมาณที่แน่นอนให้เป็นค่าคงที่ 0: $F_0(x) = 0$

หมายเหตุ: รหัสต่อไปนี้มีไว้สำหรับความช่วยเหลือด้านการศึกษาเท่านั้น ในทางปฏิบัติ คุณเพียงแค่โทรหา tfdf.keras.GradientBoostedTreeModel

# Simplified example of regressive gradient boosting.

y = ... # the labels
x = ... # the features

strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.

for i in range(num_iters):

    # Error of the strong model
    error = strong_predictions - y

    # The weak model is a decision tree (see CART chapter)
    # without pruning and a maximum depth of 3.
    weak_model = tfdf.keras.CartModel(
        task=tfdf.keras.Task.REGRESSION,
        validation_ratio=0.0,
        max_depth=3)
    weak_model.fit(x=x, y=error)

    strong_model.append(weak_model)

    weak_predictions = weak_model.predict(x)[:,0]

    strong_predictions -= weak_predictions

มาลองใช้โค้ดนี้กับชุดข้อมูลต่อไปนี้กัน

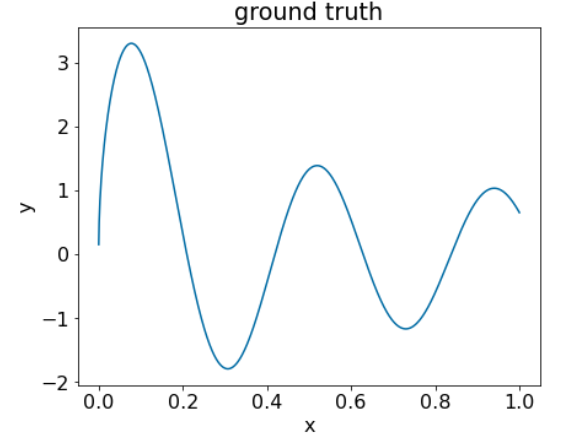
รูปที่ 25 ชุดข้อมูลการถดถอยสังเคราะห์ที่มีฟีเจอร์ตัวเลข 1 รายการ

 

แผนภูมิ 3 รายการต่อไปนี้แสดงหลังจากการวนซ้ำครั้งแรกของอัลกอริทึมการเพิ่มประสิทธิภาพด้วยการเพิ่มเชิงลาด

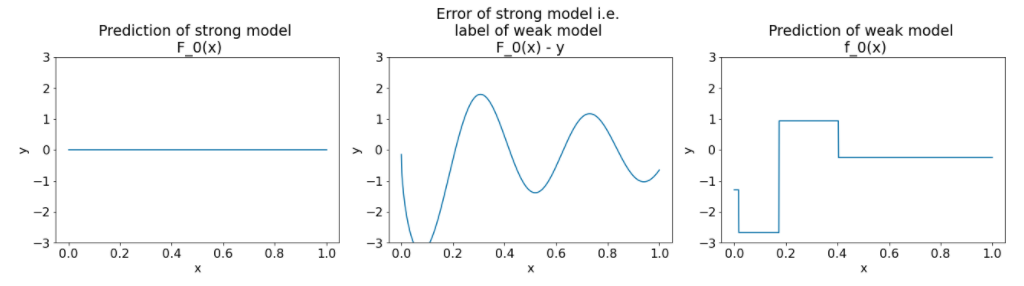
รูปที่ 26 ผัง 3 ผังหลังจากการทำซ้ำครั้งแรก

 

โปรดทราบข้อมูลต่อไปนี้เกี่ยวกับผังในรูปที่ 26

• ผังแรกแสดงการคาดการณ์ของโมเดลที่มีประสิทธิภาพ ซึ่งปัจจุบันจะเท่ากับ 0 เสมอ
• ผังภาพที่ 2 แสดงข้อผิดพลาด ซึ่งเป็นป้ายกํากับของโมเดลที่มีประสิทธิภาพต่ำ
• ผังภาพที่ 3 แสดงโมเดลที่มีประสิทธิภาพต่ำ

โมเดลที่มีประสิทธิภาพต่ำแบบแรกกำลังเรียนรู้การนำเสนอแบบหยาบของป้ายกำกับและส่วนใหญ่จะมุ่งเน้นที่ส่วนซ้ายของพื้นที่ลักษณะ (ส่วนที่มีความหลากหลายมากที่สุด และจึงมีข้อผิดพลาดมากที่สุดสําหรับโมเดลที่ไม่ถูกต้องแบบคงที่)

ด้านล่างนี้คือผังเดียวกันสำหรับอีกรอบหนึ่งของอัลกอริทึม

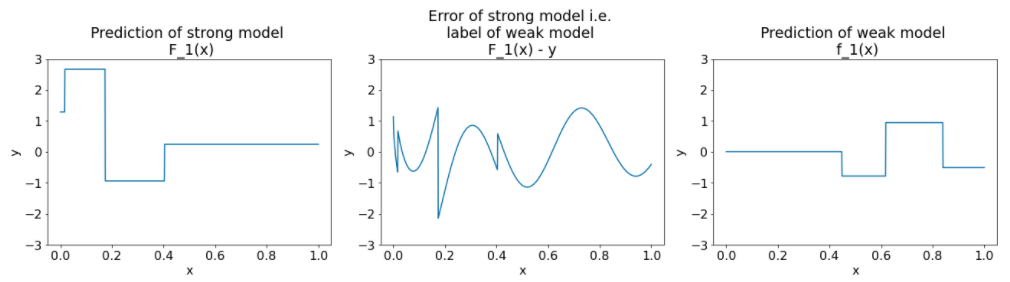
รูปที่ 27 ผัง 3 รายการหลังจากการวนซ้ำครั้งที่ 2

 

โปรดทราบข้อมูลต่อไปนี้เกี่ยวกับผังในรูปที่ 27

• ตอนนี้โมเดลที่มีประสิทธิภาพจะมีข้อมูลการคาดการณ์ของโมเดลที่มีประสิทธิภาพต่ำของการทำซ้ำก่อนหน้า
• ความคลาดเคลื่อนใหม่ของโมเดลที่มีประสิทธิภาพสูงจะน้อยกว่าเล็กน้อย
• การคาดการณ์ใหม่ของโมเดลที่มีประสิทธิภาพต่ำตอนนี้มุ่งเน้นที่ส่วนด้านขวาของพื้นที่ลักษณะ

เราเรียกใช้อัลกอริทึมซ้ำอีก 8 ครั้ง ดังนี้

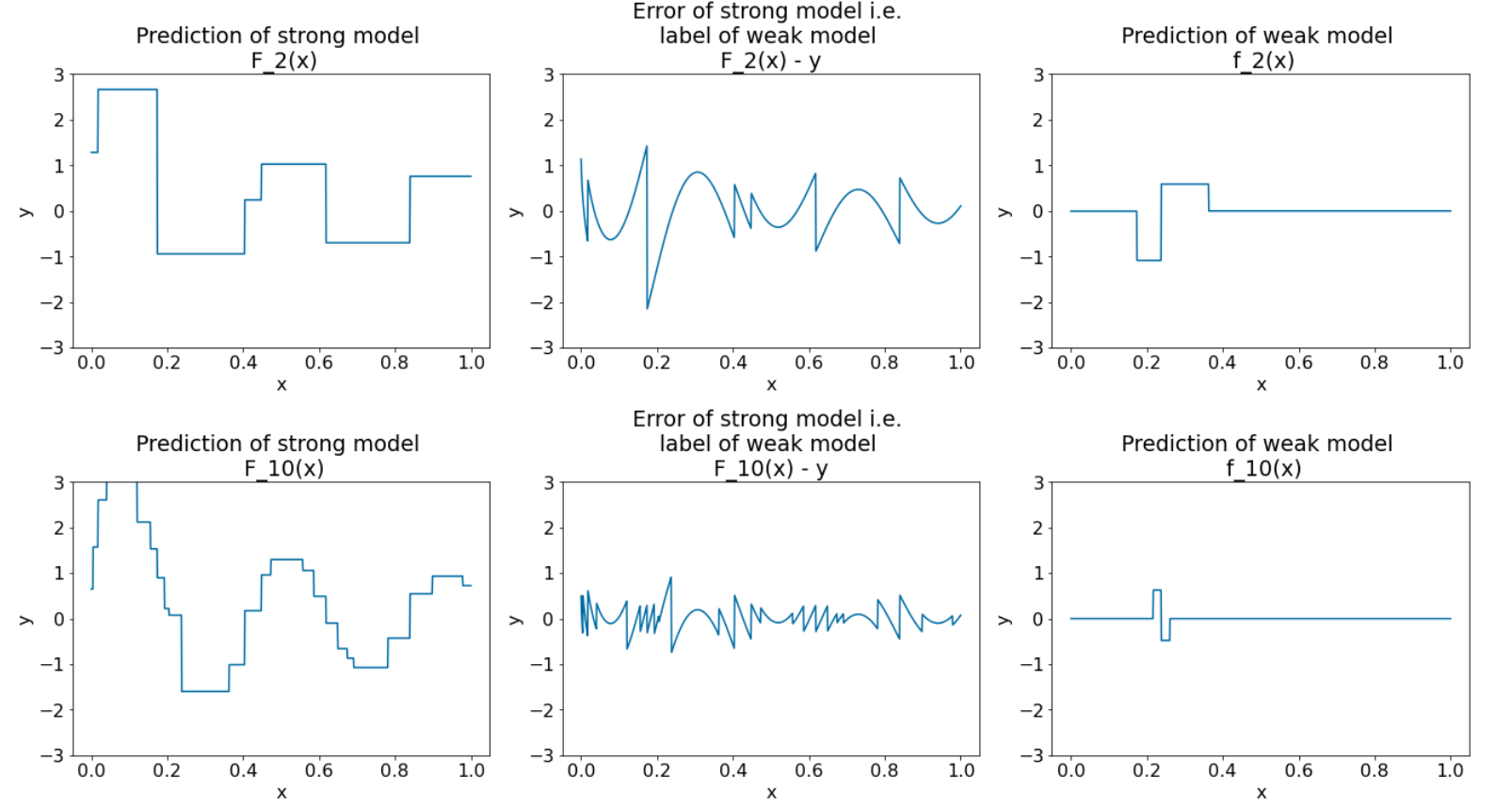
รูปที่ 28 ผัง 3 รายการหลังจากการวนซ้ำครั้งที่ 3 และครั้งที่ 10

 

ในรูปที่ 28 โปรดสังเกตว่าการคาดการณ์ของโมเดลที่มีประสิทธิภาพเริ่มคล้ายกับผังชุดข้อมูล

ตัวเลขเหล่านี้แสดงอัลกอริทึมการเพิ่มประสิทธิภาพด้วย Gradient Boosting โดยใช้ต้นไม้การตัดสินใจเป็นอัลกอริทึมการเรียนรู้แบบอ่อน การผสมผสานนี้เรียกว่าต้นไม้ (การตัดสินใจ) ที่เพิ่มประสิทธิภาพด้วย Gradient

ผังก่อนหน้าแสดงถึงแก่นแท้ของการเพิ่มประสิทธิภาพด้วย Gradient อย่างไรก็ตาม ตัวอย่างนี้ไม่มีการดำเนินการ 2 รายการต่อไปนี้ซึ่งเกิดขึ้นจริง

• การลดลง
• การเพิ่มประสิทธิภาพค่าใบด้วยวิธีของนิวตัน 1 ขั้นตอน

หมายเหตุ: ในทางปฏิบัติ อัลกอริทึมการเพิ่มประสิทธิภาพด้วยการเพิ่มการลาดชันมีหลายรูปแบบที่มีการดำเนินการอื่นๆ

การหดตัว

โมเดลที่อ่อนแอ $f_i$ จะคูณด้วยค่าเล็กๆ $\nu$ (เช่น $\nu = 0.1$) ก่อนที่จะเพิ่มลงในโมเดลที่แข็งแกร่ง $F_i$ ค่าเล็กๆ นี้เรียกว่าการหดตัว กล่าวคือ แทนที่จะใช้สูตรต่อไปนี้ในการวนซ้ำแต่ละครั้ง

\[ F_{i+1} = F_i - f_i \]

แต่ละรอบจะใช้สูตรต่อไปนี้

\[ F_{i+1} = F_i - \nu f_i \]

การลดลงในการเพิ่มประสิทธิภาพด้วย Gradient Boosting นั้นคล้ายกับอัตราการเรียนรู้ในโครงข่ายประสาทเทียม การลดขนาดควบคุมความเร็วในการเรียนรู้ของโมเดลที่มีประสิทธิภาพ ซึ่งช่วยจำกัดการจับคู่ที่มากเกินไป กล่าวคือ ค่าการหดตัวที่ใกล้กับ 0.0 จะช่วยลดการพอดีมากเกินไปได้มากกว่าค่าการหดตัวที่ใกล้กับ 1.0

ในโค้ดด้านบน เราจะใช้การหดตัวดังนี้

shrinkage = 0.1   # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions