与抽样和提升类似,梯度提升是一种在其他机器学习算法之上应用的方法。非正式地讲,梯度提升涉及两种类型的模型:
- “弱”机器学习模型,通常是决策树。
- 由多个弱模型组成的“强”机器学习模型。
在梯度提升中,每个步骤都会训练一个新的弱模型来预测当前强模型的“误差”(称为伪响应)。我们稍后会详细介绍“错误”状态。目前,假设“误差”是预测值与回归标签之间的差值。然后,将弱模型(即“误差”)添加到强模型中,并带有负号,以减少强模型的误差。
梯度提升是迭代过程。每个迭代都会调用以下公式:
\[ F_{i+1} = F_i - f_i \]
其中:
- $F_i$ 是第 $i$ 步中的强模型。
- $f_i$ 是第 $i$ 步的弱模型。
此操作会重复进行,直到满足停止条件(例如迭代次数上限),或者(强)模型开始过拟合(根据单独的验证数据集衡量)。
我们将通过一个简单的回归数据集来演示梯度提升,其中:
- 目标是根据 $x$ 预测 $y$。
- 强模型会初始化为零常量:$F_0(x) = 0$。
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
我们将此代码应用于以下数据集:
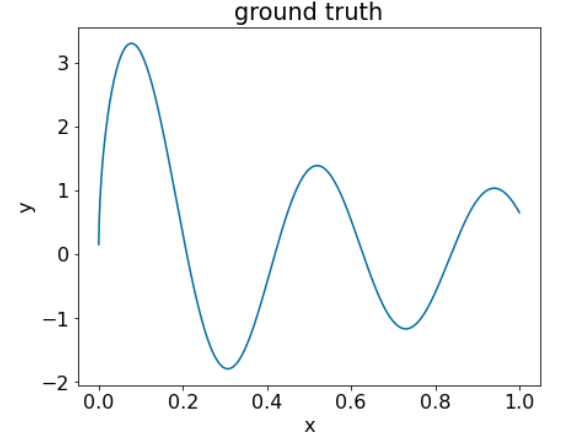
图 25. 包含一个数值特征的合成回归数据集。
以下是梯度提升算法进行第一次迭代后的三个图表:
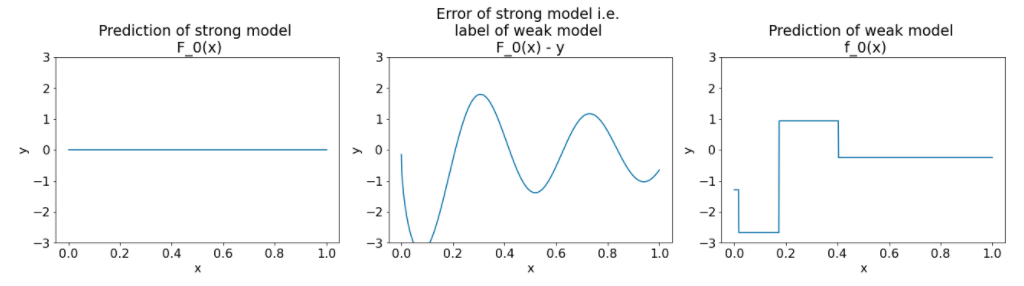
图 26. 第一次迭代后的三个图表。
请注意图 26 中的图表:
- 第一个图表显示了强大模型的预测结果,目前始终为 0。
- 第二个图表显示了错误,即弱模型的标签。
- 第三个图表显示了弱模型。
第一个弱模型会学习标签的大致表示,并且主要侧重于特征空间的左侧部分(变化最明显的部分,因此对于恒定错误模型,该部分的误差最大)。
以下是该算法另一个迭代的相同图表:
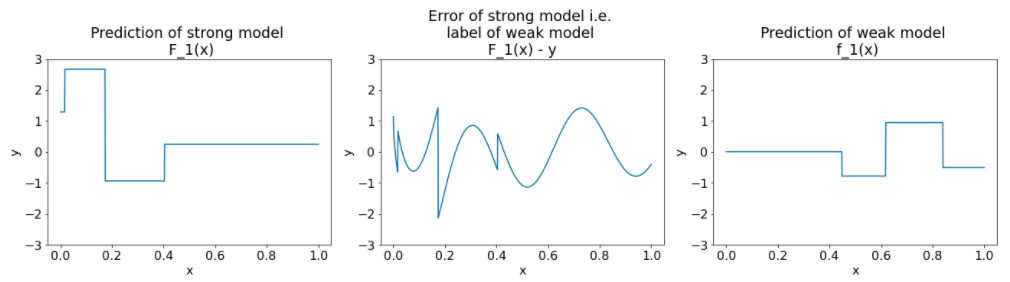
图 27. 第二次迭代后的三个图表。
请注意图 27 中的图表:
- 强模型现在包含上一次迭代中弱模型的预测结果。
- 强大模型的新误差略小。
- 弱模型的新预测现在侧重于特征空间的右侧。
我们再运行 8 次算法迭代:
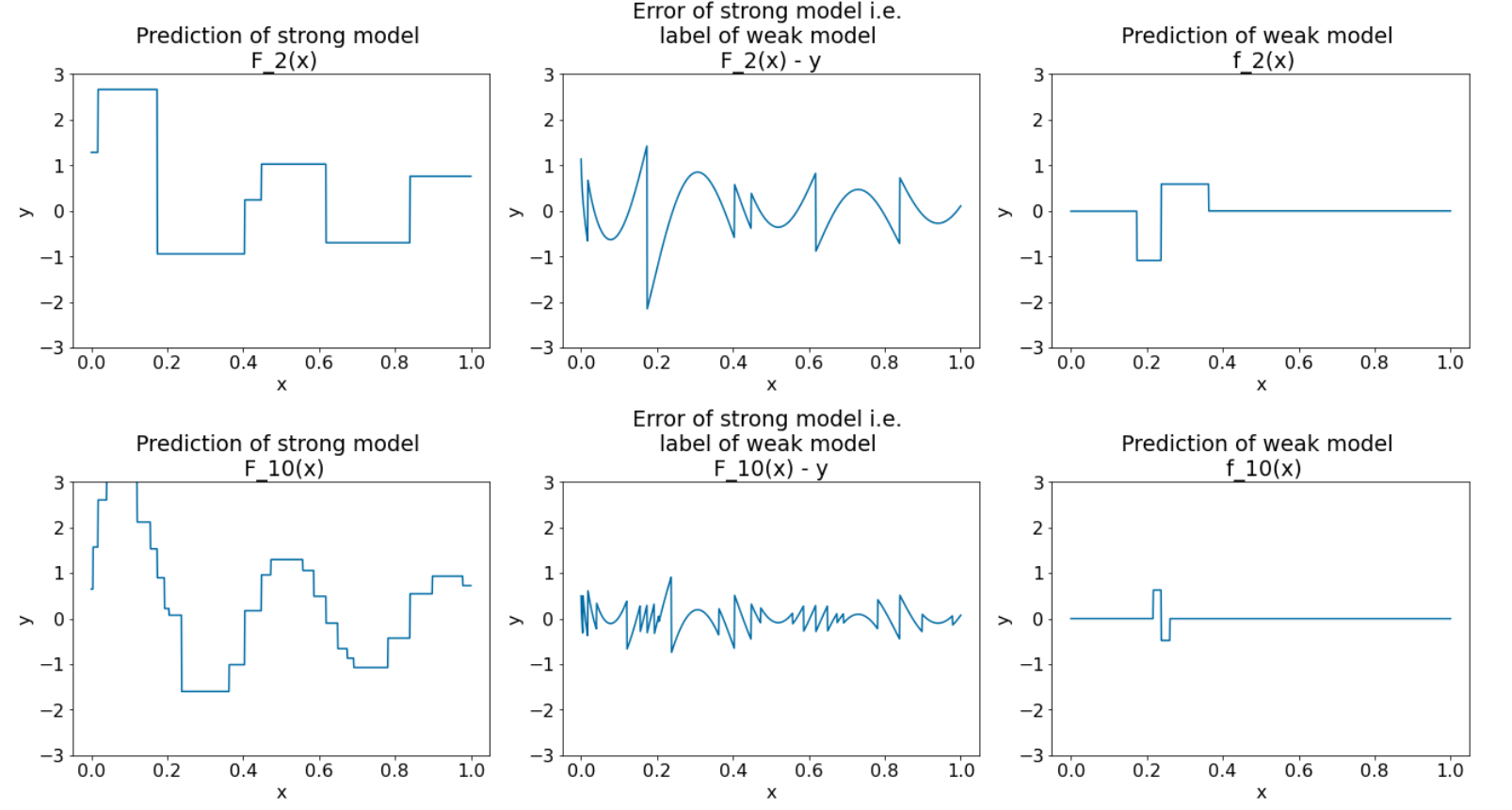
图 28. 第三次迭代和第十次迭代后的三个图。
请注意,在图 28 中,强大模型的预测结果开始类似于数据集的图。
这些图展示了使用决策树作为弱学习器的梯度提升算法。这种组合称为梯度提升(决策)树。
上述图表揭示了梯度提升的精髓。不过,此示例缺少以下两项实际操作:
- 收缩
- 使用牛顿法的一步对叶值进行优化
缩水
弱模型 $f_i$ 会先乘以一个小值 $\nu$(例如 $\nu = 0.1$),然后再添加到强模型 $F_i$。此小值称为收缩。换句话说,在每次迭代中,请使用以下公式:
\[ F_{i+1} = F_i - f_i \]
每个迭代都使用以下公式:
\[ F_{i+1} = F_i - \nu f_i \]
梯度提升中的收缩类似于神经网络中的学习率。收缩控制强大模型的学习速度,有助于限制过拟合。也就是说,收缩值越接近 0.0,过拟合程度就越小,而收缩值越接近 1.0,过拟合程度就越大。
在上面的代码中,缩减会按如下方式实现:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
