Gradient Boosted Decision Trees

Like bagging and boosting, gradient boosting is a methodology applied on top of another machine learning algorithm. Informally, gradient boosting involves two types of models:

a "weak" machine learning model, which is typically a decision tree.
a "strong" machine learning model, which is composed of multiple weak models.

In gradient boosting, at each step, a new weak model is trained to predict the "error" of the current strong model (which is called the pseudo response). We will detail "error" later. For now, assume "error" is the difference between the prediction and a regressive label. The weak model (that is, the "error") is then added to the strong model with a negative sign to reduce the error of the strong model.

Gradient boosting is iterative. Each iteration invokes the following formula:

\[ F_{i+1} = F_i - f_i \]

where:

$F_i$ is the strong model at step $i$.
$f_i$ is the weak model at step $i$.

This operation repeats until a stopping criterion is met, such as a maximum number of iterations or if the (strong) model begins to overfit as measured on a separate validation dataset.

Let's illustrate gradient boosting on a simple regression dataset where:

The objective is to predict $y$ from $x$.
The strong model is initialized to be a zero constant: $F_0(x) = 0$.

# Simplified example of regressive gradient boosting.

y = ... # the labels
x = ... # the features

strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.

for i in range(num_iters):

    # Error of the strong model
    error = strong_predictions - y

    # The weak model is a decision tree (see CART chapter)
    # without pruning and a maximum depth of 3.
    weak_model = tfdf.keras.CartModel(
        task=tfdf.keras.Task.REGRESSION,
        validation_ratio=0.0,
        max_depth=3)
    weak_model.fit(x=x, y=error)

    strong_model.append(weak_model)

    weak_predictions = weak_model.predict(x)[:,0]

    strong_predictions -= weak_predictions

Let's apply this code on the following dataset:

A plot of ground truth for one feature, x, and its label, y. The plot is a
series of somewhat damped sine
waves.

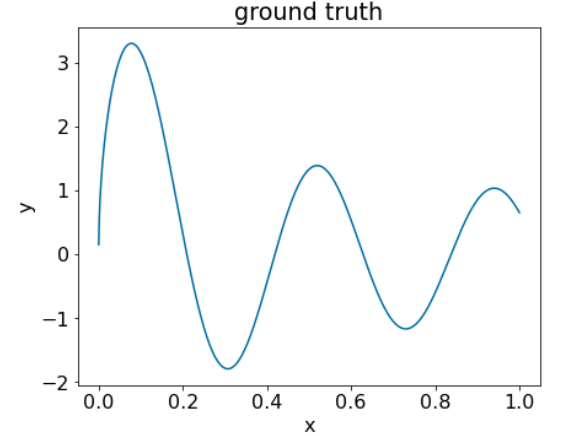
Figure 25. A synthetic regressive dataset with one numerical feature.

Here are three plots after the first iteration of the gradient boosting algorithm:

Three plots. The first plot shows the prediction of the strong model, which is
a straight line of slope 0 and y-intercept 0. The second plot shows the error of
the strong model, which is a series of sine waves. The third plot shows the
prediction of the weak model, which is a set of square
waves.

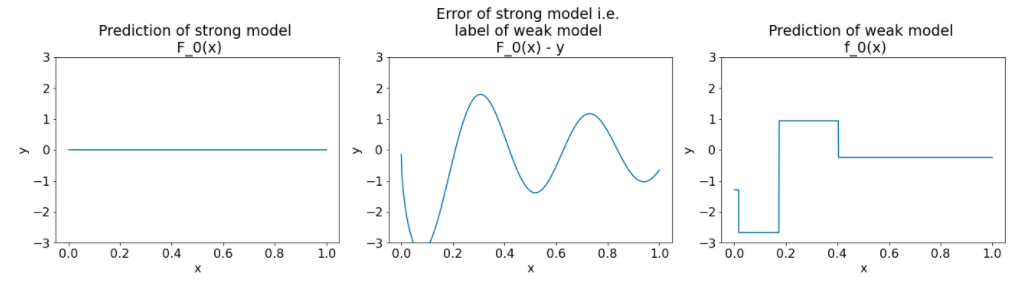
Figure 26. Three plots after the first iteration.

Note the following about the plots in Figure 26:

The first plot shows the predictions of the strong model, which is currently always 0.
The second plot shows the error, which is the label of the weak model.
The third plot shows the weak model.

The first weak model is learning a coarse representation of the label and mostly focuses on the left part of the feature space (the part with the most variation, and therefore the most error for the constant wrong model).

Following are the same plots for another iteration of the algorithm:

Three plots. The first plot shows the prediction of the strong model, which is
an inverse of the plot of the prediction of the weak model from the previous
Figure. The second plot shows the error of the strong model, which is a noisy
set of sine waves. The third plot shows the prediction of the weak model, which
is a couple of square
waves.

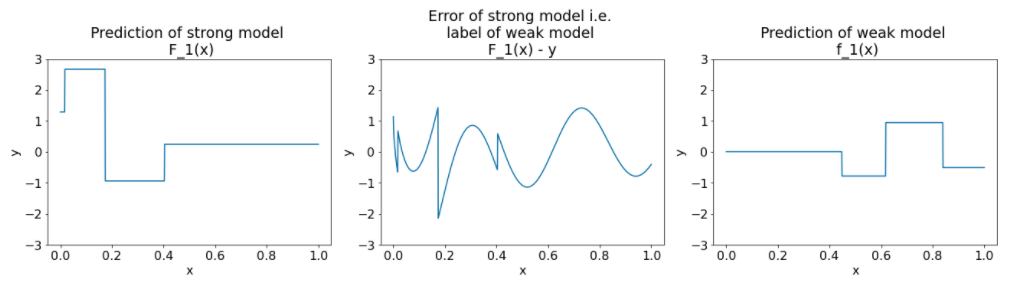
Figure 27. Three plots after the second iteration.

Note the following about the plots in Figure 27:

The strong model now contains the prediction of the weak model of the previous iteration.
The new error of the strong model is a bit smaller.
The new prediction of the weak model now focuses on the right part of the feature space.

We run the algorithm for 8 more iterations:

The plots show the strong model gradually becoming closer to ground truth
while the prediction of the weak model gradually becomes, well,
weaker.

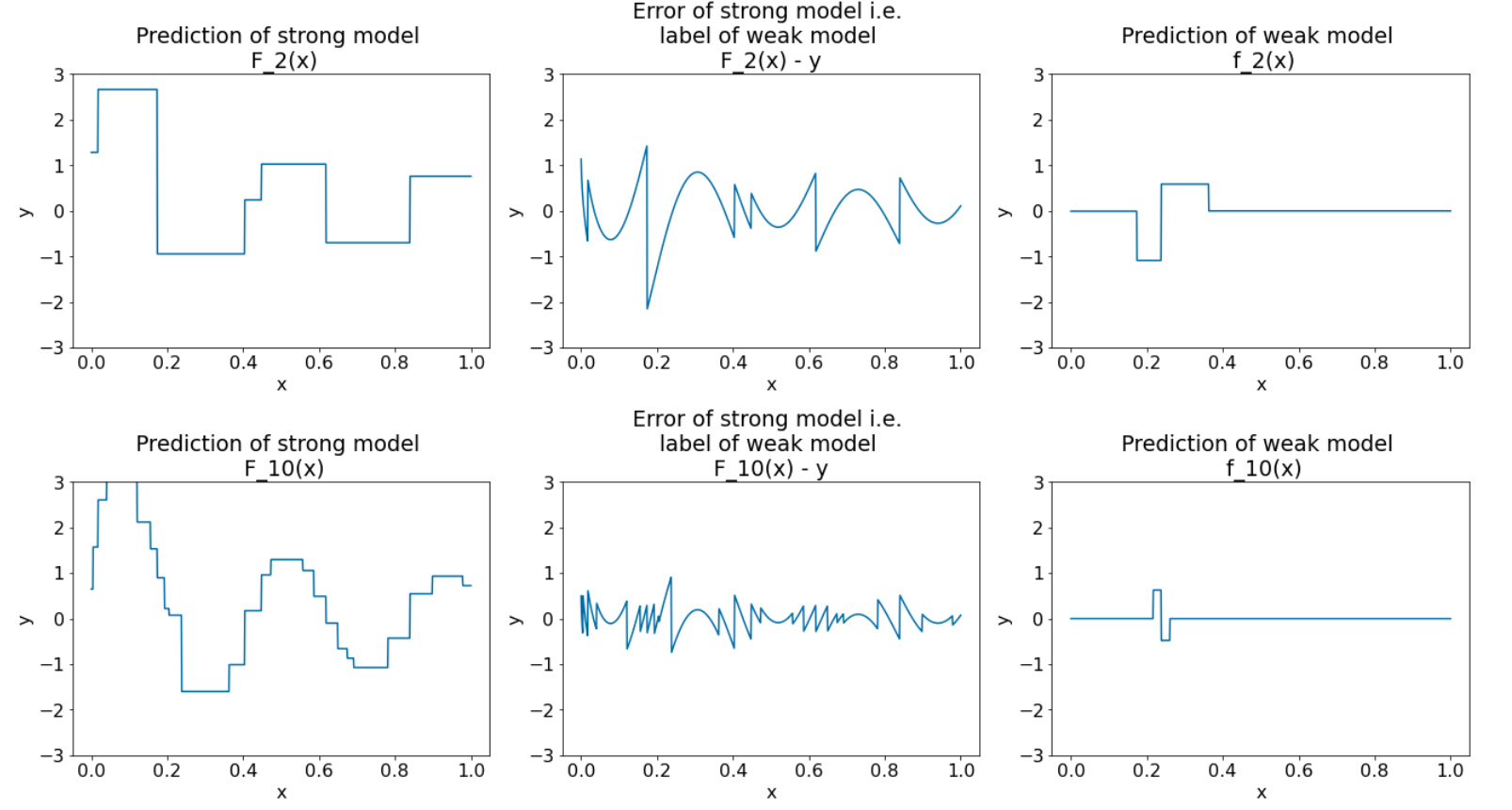
Figure 28. Three plots after the third iteration and the tenth iteration.

In Figure 28, note that the prediction of strong model starts to resemble the plot of the dataset.

These figures illustrate the gradient boosting algorithm using decision trees as weak learners. This combination is called gradient boosted (decision) trees.

The preceding plots suggest the essence of gradient boosting. However, this example lacks the following two real-world operations:

The shrinkage
The optimization of leaf values with one step of Newton's method

Shrinkage

The weak model $f_i$ is multiplied by a small value $\nu$ (for example, $\nu = 0.1$) before being added to the strong model $F_i$. This small value is called the shrinkage. In other words, instead of each iteration using the following formula:

\[ F_{i+1} = F_i - f_i \]

Each iteration uses the following formula:

\[ F_{i+1} = F_i - \nu f_i \]

Shrinkage in gradient boosting is analogous to learning rate in neural networks. Shrinkage controls how fast the strong model is learning, which helps limit overfitting. That is, a shrinkage value closer to 0.0 reduces overfitting more than a shrinkage value closer to 1.0.

In our code above, the shrinkage would be implemented as follows:

shrinkage = 0.1   # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions