Al igual que el bagging y el boosting, el aumento de gradientes es una metodología que se aplica sobre otro algoritmo de aprendizaje automático. De manera informal, el aumento de gradiente implica dos tipos de modelos:
- un modelo de aprendizaje automático "débil", que suele ser un árbol de decisión.
- un modelo de aprendizaje automático "sólido", que se compone de varios modelos débiles.
En el aumento de gradiente, en cada paso, se entrena un nuevo modelo débil para predecir el “error” del modelo fuerte actual (que se denomina respuesta pseudo). Más adelante, detallaremos el "error". Por ahora, supongamos que el “error” es la diferencia entre la predicción y una etiqueta regresiva. Luego, el modelo débil (es decir, el “error”) se agrega al modelo fuerte con un signo negativo para reducir el error del modelo fuerte.
La potenciación del gradiente es iterativa. Cada iteración invoca la siguiente fórmula:
\[ F_{i+1} = F_i - f_i \]
Donde:
- $F_i$ es el modelo sólido en el paso $i$.
- $f_i$ es el modelo débil en el paso $i$.
Esta operación se repite hasta que se cumple un criterio de detención, como una cantidad máxima de iteraciones o si el modelo (fuerte) comienza a sobreajustarse según se mide en un conjunto de datos de validación independiente.
Veamos el aumento de gradiente en un conjunto de datos de regresión simple en el que se cumplen las siguientes condiciones:
- El objetivo es predecir $y$ a partir de $x$.
- El modelo fuerte se inicializa para ser una constante cero: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Apliquemos este código en el siguiente conjunto de datos:
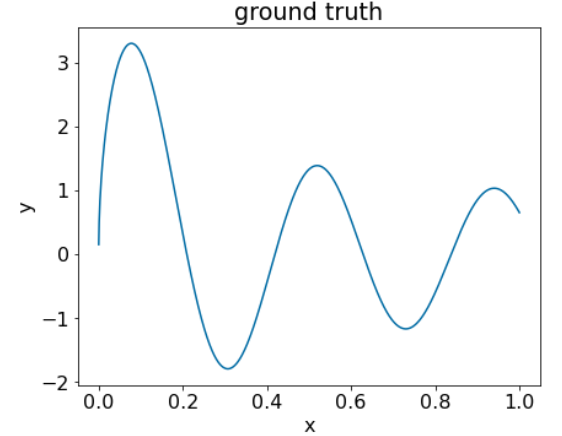
Figura 25. Un conjunto de datos regresivo sintético con una característica numérica.
Estas son tres gráficas después de la primera iteración del algoritmo de aumento de gradientes:
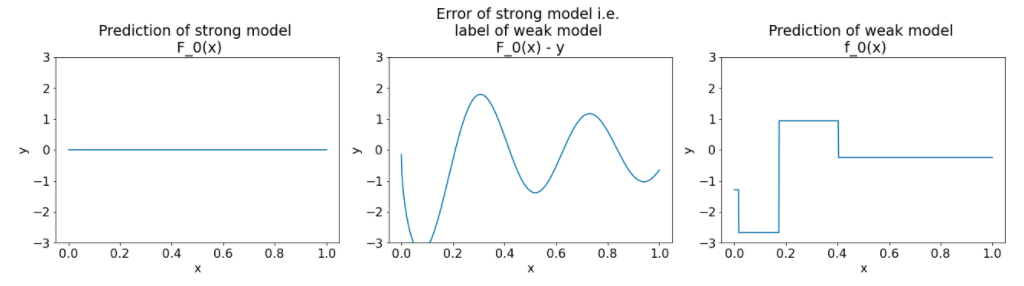
Figura 26. Tres gráficos después de la primera iteración.
Ten en cuenta lo siguiente sobre los gráficos de la Figura 26:
- El primer gráfico muestra las predicciones del modelo sólido, que actualmente siempre es 0.
- El segundo gráfico muestra el error, que es la etiqueta del modelo débil.
- El tercer gráfico muestra el modelo débil.
El primer modelo débil aprende una representación aproximada de la etiqueta y se enfoca principalmente en la parte izquierda del espacio de características (la parte con más variación y, por lo tanto, con más errores para el modelo incorrecto constante).
A continuación, se muestran los mismos gráficos para otra iteración del algoritmo:
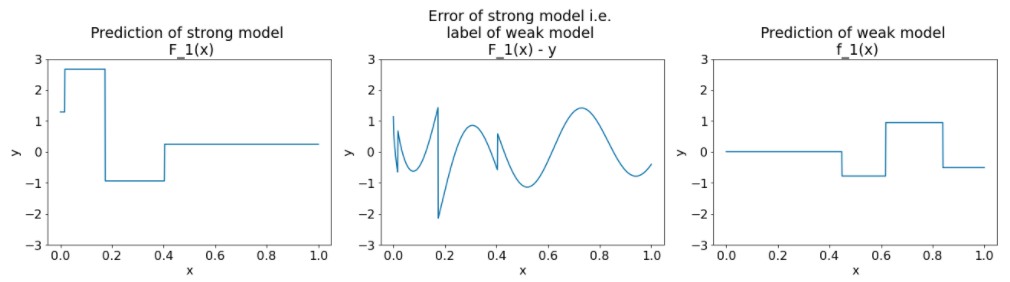
Figura 27. Tres parcelas después de la segunda iteración.
Ten en cuenta lo siguiente sobre los gráficos de la Figura 27:
- El modelo sólido ahora contiene la predicción del modelo débil de la iteración anterior.
- El nuevo error del modelo sólido es un poco menor.
- La nueva predicción del modelo débil ahora se enfoca en la parte derecha del espacio de características.
Ejecutamos el algoritmo para 8 iteraciones más:
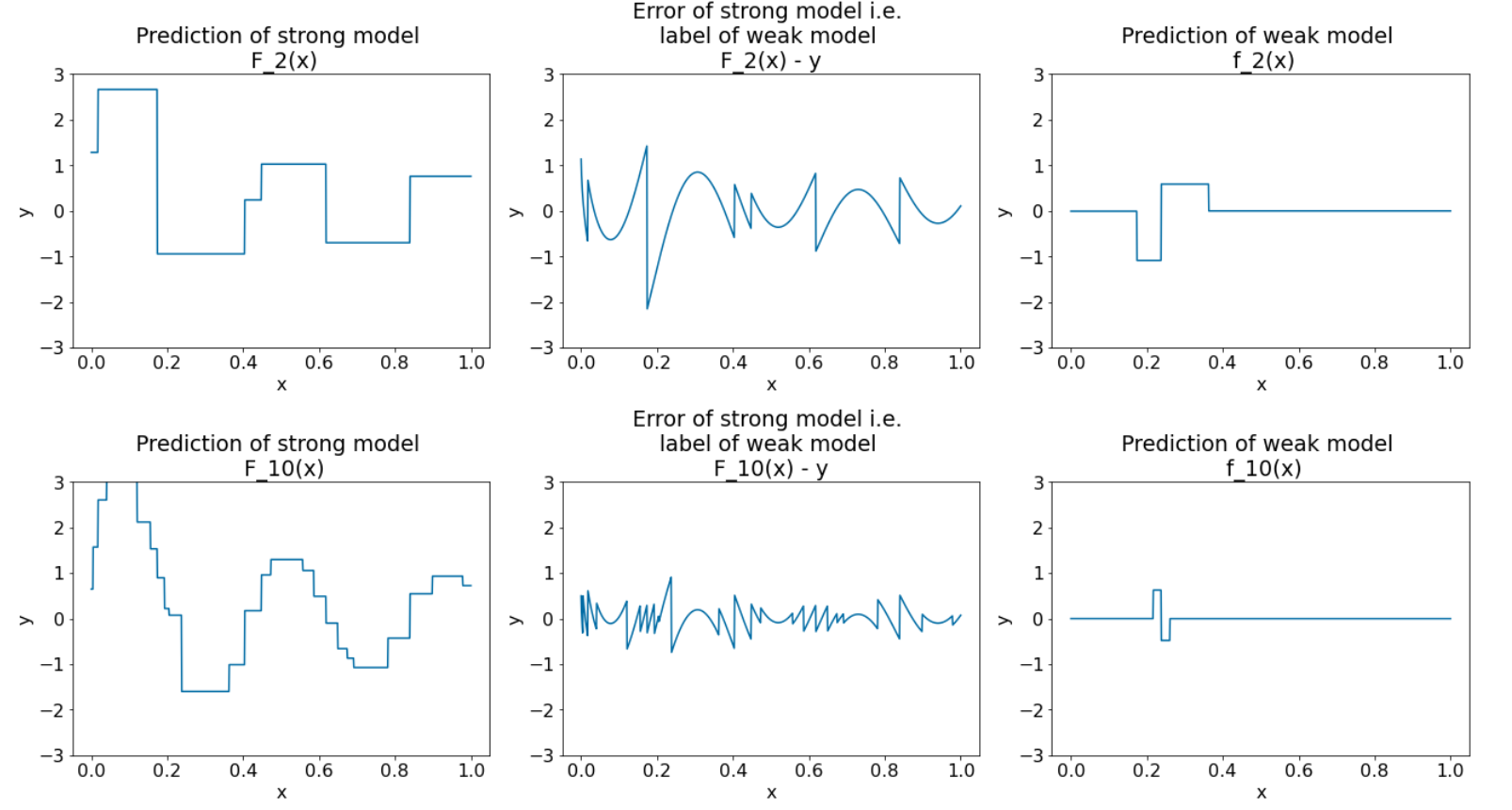
Figura 28. Tres gráficos después de la tercera iteración y la décima iteración.
En la Figura 28, observa que la predicción del modelo sólido comienza a parecerse a la trama del conjunto de datos.
Estas figuras ilustran el algoritmo de boosting del gradiente con árboles de decisión como aprendientes débiles. Esta combinación se denomina árboles (de decisión) mejorados con gradientes.
Los gráficos anteriores sugieren la esencia del aumento de gradiente. Sin embargo, a este ejemplo le faltan las siguientes dos operaciones del mundo real:
- La contracción
- La optimización de los valores de hoja con un paso del método de Newton
Encogimiento
El modelo débil $f_i$ se multiplica por un valor pequeño $\nu$ (por ejemplo, $\nu = 0.1$) antes de agregarse al modelo fuerte $F_i$. Este valor pequeño se denomina reducción. En otras palabras, en lugar de que cada iteración use la siguiente fórmula:
\[ F_{i+1} = F_i - f_i \]
Cada iteración usa la siguiente fórmula:
\[ F_{i+1} = F_i - \nu f_i \]
La contracción en el aumento de gradientes es análoga a la tasa de aprendizaje en las redes neuronales. La contracción controla la velocidad a la que aprende el modelo sólido, lo que ayuda a limitar la sobreajuste. Es decir, un valor de contracción más cercano a 0.0 reduce el sobreajuste más que un valor de contracción más cercano a 1.0.
En nuestro código anterior, la contracción se implementaría de la siguiente manera:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
