Seperti bagging dan boosting, gradient boosting adalah metodologi yang diterapkan di atas algoritma machine learning lainnya. Secara informal, peningkatan gradien melibatkan dua jenis model:
- model machine learning "lemah", yang biasanya berupa pohon keputusan.
- model machine learning "kuat", yang terdiri dari beberapa model lemah.
Dalam gradient boosting, pada setiap langkah, model lemah baru dilatih untuk memprediksi "error" model kuat saat ini (yang disebut respons pseudo). Kita akan menjelaskan "error" nanti. Untuk saat ini, asumsikan "error" adalah perbedaan antara prediksi dan label regresif. Model lemah (yaitu, "error") kemudian ditambahkan ke model kuat dengan tanda negatif untuk mengurangi error model kuat.
Peningkatan gradien bersifat iteratif. Setiap iterasi memanggil formula berikut:
\[ F_{i+1} = F_i - f_i \]
dalam hal ini:
- $F_i$ adalah model kuat pada langkah $i$.
- $f_i$ adalah model lemah pada langkah $i$.
Operasi ini berulang hingga kriteria penghentian terpenuhi, seperti jumlah iterasi maksimum atau jika model (kuat) mulai mengalami overfitting seperti yang diukur pada set data validasi terpisah.
Mari kita ilustrasikan peningkatan gradien pada set data regresi sederhana dengan:
- Tujuannya adalah untuk memprediksi $y$ dari $x$.
- Model kuat diinisialisasi menjadi konstanta nol: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Mari kita terapkan kode ini pada set data berikut:
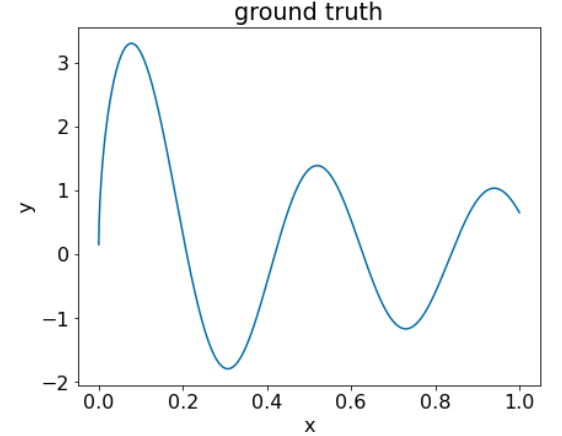
Gambar 25. Set data regresi sintetis dengan satu fitur numerik.
Berikut adalah tiga plot setelah iterasi pertama algoritma gradient boosting:
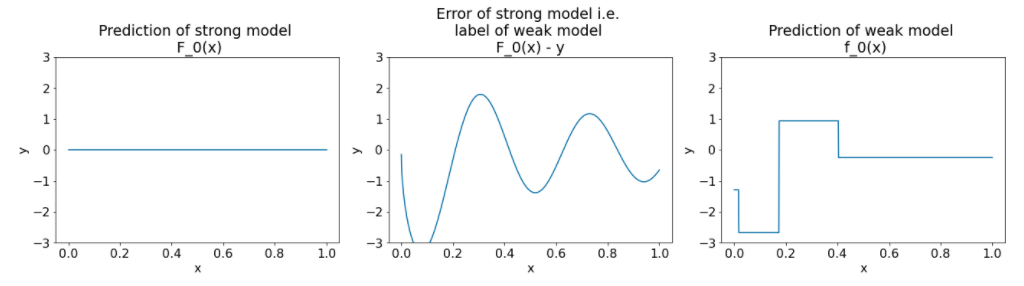
Gambar 26. Tiga plot setelah iterasi pertama.
Perhatikan hal-hal berikut tentang plot dalam Gambar 26:
- Plot pertama menunjukkan prediksi model kuat, yang saat ini selalu 0.
- Plot kedua menunjukkan error, yang merupakan label model lemah.
- Plot ketiga menunjukkan model yang lemah.
Model lemah pertama mempelajari representasi kasar label dan sebagian besar berfokus pada bagian kiri ruang fitur (bagian dengan variasi terbanyak, sehingga memiliki error terbanyak untuk model yang salah secara konstan).
Berikut adalah plot yang sama untuk iterasi algoritma lainnya:

Gambar 27. Tiga plot setelah iterasi kedua.
Perhatikan hal-hal berikut tentang plot dalam Gambar 27:
- Model kuat kini berisi prediksi model lemah dari iterasi sebelumnya.
- Error baru dari model yang kuat sedikit lebih kecil.
- Prediksi baru model lemah kini berfokus pada bagian kanan ruang fitur.
Kita menjalankan algoritma untuk 8 iterasi lagi:
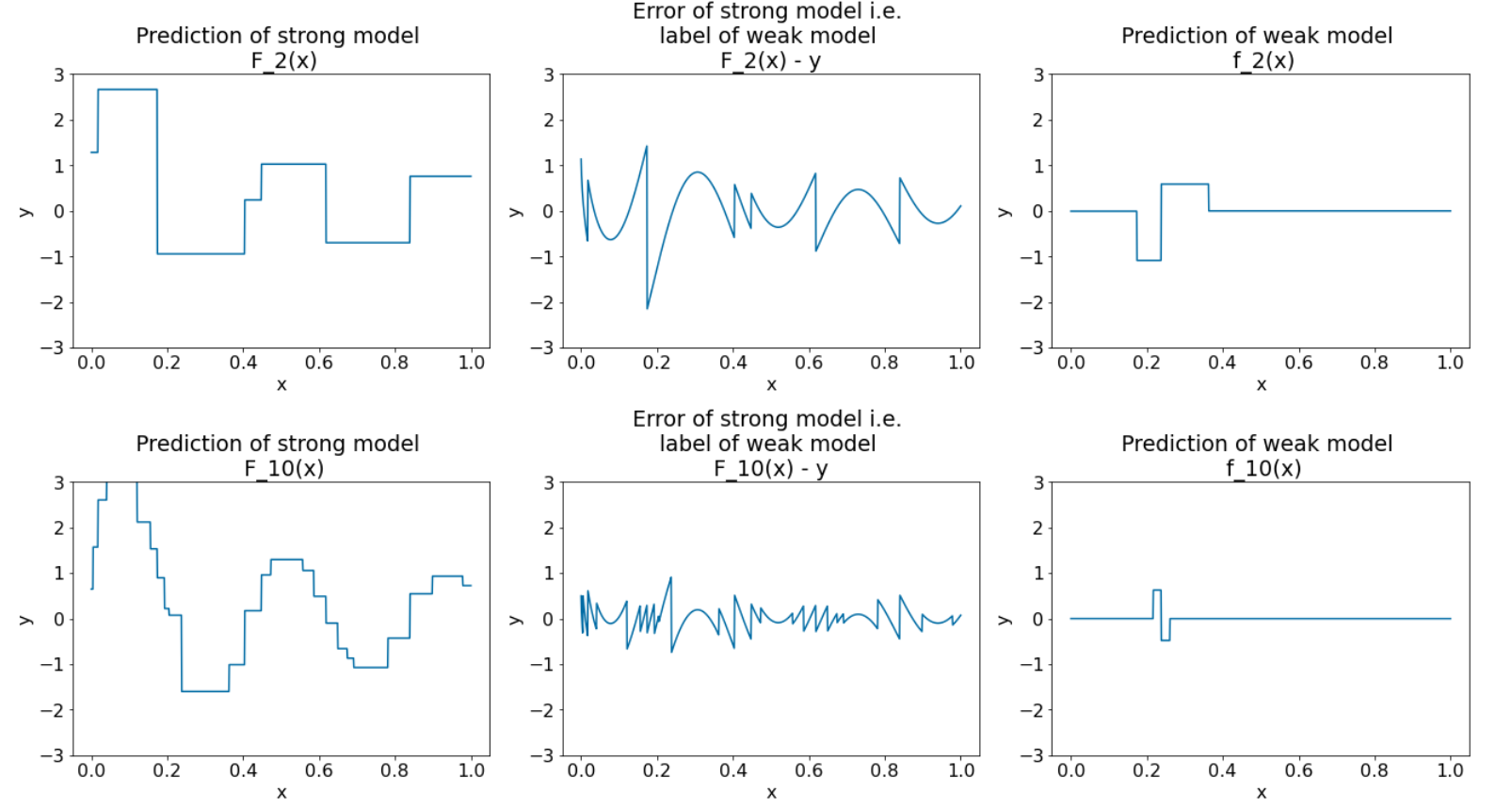
Gambar 28. Tiga plot setelah iterasi ketiga dan iterasi kesepuluh.
Pada Gambar 28, perhatikan bahwa prediksi model yang kuat mulai menyerupai plot set data.
Gambar ini menggambarkan algoritma gradient boosting menggunakan pohon keputusan sebagai pembelajar lemah. Kombinasi ini disebut pohon (keputusan) dengan penguatan gradien.
Plot sebelumnya menunjukkan esensi gradient boosting. Namun, contoh ini tidak memiliki dua operasi dunia nyata berikut:
- Penyusutan
- Pengoptimalan nilai daun dengan satu langkah metode Newton
Penyusutan
Model lemah $f_i$ dikalikan dengan nilai kecil $\nu$ (misalnya, $\nu = 0,1$) sebelum ditambahkan ke model kuat $F_i$. Nilai kecil ini disebut penyingkatan. Dengan kata lain, bukan setiap iterasi menggunakan formula berikut:
\[ F_{i+1} = F_i - f_i \]
Setiap iterasi menggunakan formula berikut:
\[ F_{i+1} = F_i - \nu f_i \]
Pengecilan dalam gradient boosting analog dengan kecepatan belajar dalam jaringan neural. Pengecilan mengontrol seberapa cepat model yang kuat belajar, yang membantu membatasi overfitting. Artinya, nilai penyusutan yang lebih dekat ke 0,0 akan mengurangi overfitting lebih banyak daripada nilai penyusutan yang lebih dekat ke 1,0.
Dalam kode di atas, penyusutan akan diterapkan sebagai berikut:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
