bagging 및 boosting과 마찬가지로, 경사 부스팅은 다른 머신러닝 알고리즘 위에 적용되는 방법론입니다. 비공식적으로 경사 부스팅에는 다음 두 가지 유형의 모델이 포함됩니다.
- '약한' 머신러닝 모델(일반적으로 결정 트리)
- 여러 약한 모델로 구성된 '강력한' 머신러닝 모델
경사 부스팅에서는 각 단계에서 새로운 약한 모델이 현재 강력한 모델의 '오류'(의사 응답이라고 함)를 예측하도록 학습됩니다. '오류'에 대해서는 나중에 자세히 설명하겠습니다. 지금은 '오류'가 예측과 회귀 라벨의 차이라고 가정합니다. 그런 다음 약한 모델 (즉, '오류')을 강한 모델에 음수 기호로 추가하여 강한 모델의 오류를 줄입니다.
경사 부스팅은 반복적입니다. 각 반복은 다음 수식을 호출합니다.
\[ F_{i+1} = F_i - f_i \]
각 항목의 의미는 다음과 같습니다.
- $F_i$ 는 $i$단계의 강력한 모델입니다.
- $f_i$ 는 $i$단계의 약한 모델입니다.
이 작업은 최대 반복 횟수와 같이 중지 기준이 충족될 때까지 반복되며, 별도의 검증 데이터 세트에서 측정된 대로 (강력한) 모델이 오버핏되기 시작하면 중지됩니다.
다음과 같은 간단한 회귀 데이터 세트에서 그래디언트 부스트를 설명해 보겠습니다.
- 목표는 $x$ 에서 $y$를 예측하는 것입니다.
- 강력한 모델은 0 상수($F_0(x) = 0$)로 초기화됩니다.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
다음 데이터 세트에 이 코드를 적용해 보겠습니다.
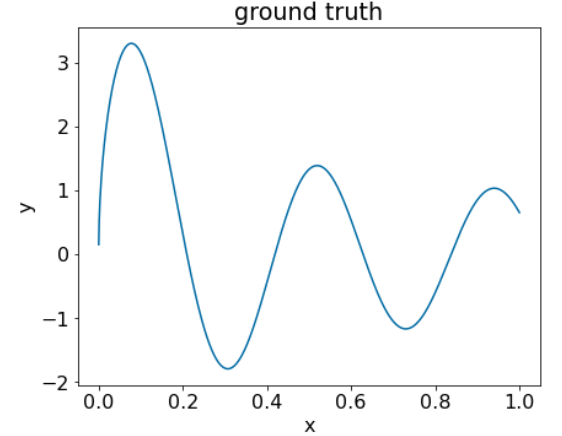
그림 25. 숫자 특성이 하나인 합성 회귀 데이터 세트입니다.
다음은 경사 부스팅 알고리즘의 첫 번째 반복 후 세 가지 그래프입니다.
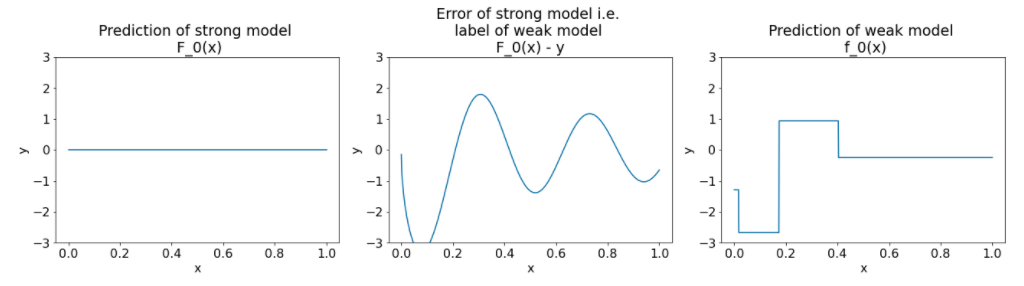
그림 26. 첫 번째 반복 후 세 개의 그래프입니다.
그림 26의 그래프에 관해 다음 사항에 유의하세요.
- 첫 번째 그래프는 강력한 모델의 예측을 보여줍니다. 현재 항상 0입니다.
- 두 번째 그래프는 약한 모델의 라벨인 오류를 보여줍니다.
- 세 번째 그래프는 약한 모델을 보여줍니다.
첫 번째 약한 모델은 라벨의 대략적인 표현을 학습하며 주로 특성 공간의 왼쪽 부분 (가장 많은 변동이 있고 따라서 잘못된 상수 모델에 가장 많은 오류가 있는 부분)에 중점을 둡니다.
다음은 알고리즘의 다른 반복에 대한 동일한 그래프입니다.
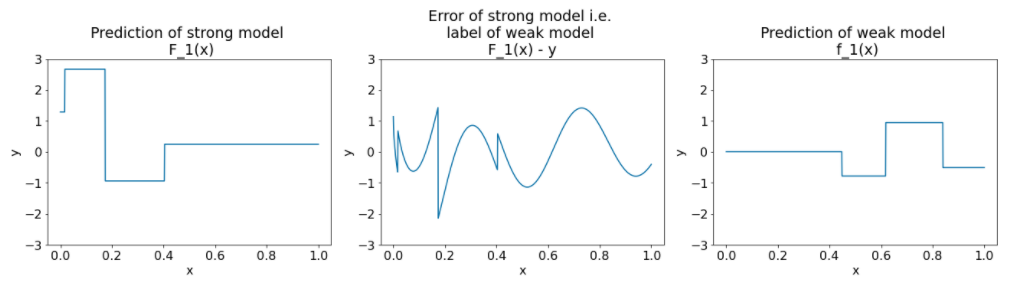
그림 27. 두 번째 반복 후 세 개의 그래프입니다.
그림 27의 그래프에 관해 다음 사항에 유의하세요.
- 이제 강력한 모델에는 이전 반복의 약한 모델 예측이 포함됩니다.
- 강력한 모델의 새 오류가 약간 더 작습니다.
- 이제 약한 모델의 새로운 예측이 특성 공간의 오른쪽 부분에 초점을 맞춥니다.
알고리즘을 8회 더 반복 실행합니다.
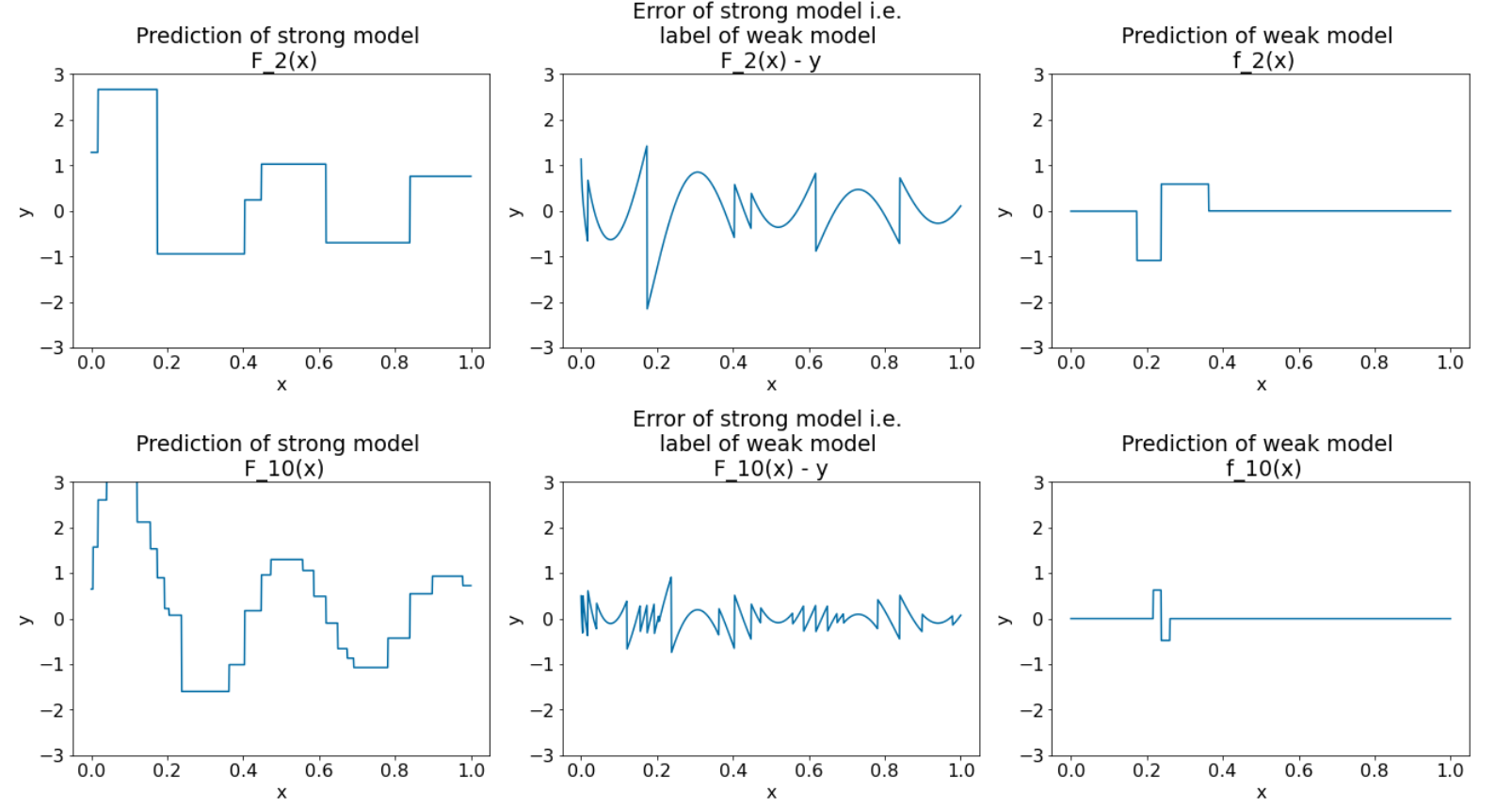
그림 28. 세 번째 반복과 열 번째 반복 후의 세 가지 그래프입니다.
그림 28에서 강력한 모델의 예측이 데이터 세트의 그래프와 유사해지기 시작합니다.
이 그림은 결정 트리를 약한 학습자로 사용하는 그래디언트 부스팅 알고리즘을 보여줍니다. 이 조합을 경사 강화 (의사 결정) 트리라고 합니다.
위의 그래프는 경사 부스팅의 핵심을 보여줍니다. 그러나 이 예에는 다음 두 가지 실제 작업이 누락되어 있습니다.
- 수축
- 뉴턴의 방법 1단계를 사용하여 리프 값 최적화
수축
약한 모델 $f_i$ 는 강한 모델 $F_i$에 추가되기 전에 작은 값 $\nu$ (예: $\nu = 0.1$)를 곱합니다. 이 작은 값을 축소라고 합니다. 즉, 각 반복에서 다음 수식을 사용하는 대신
\[ F_{i+1} = F_i - f_i \]
각 반복에서는 다음 수식을 사용합니다.
\[ F_{i+1} = F_i - \nu f_i \]
경사 부스팅의 감소는 신경망의 학습률과 유사합니다. 축소는 강력한 모델이 학습하는 속도를 제어하여 오버피팅을 제한하는 데 도움이 됩니다. 즉, 0.0에 가까운 수축 값은 1.0에 가까운 수축 값보다 오버피팅을 더 줄입니다.
위의 코드에서 축소는 다음과 같이 구현됩니다.
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
