Giống như tính năng gộp dữ liệu và tăng cường, tăng cường theo độ dốc là một phương pháp được áp dụng trên một thuật toán học máy khác. Nói một cách không chính thức, công nghệ tăng cường độ dốc liên quan đến hai loại mô hình:
- mô hình học máy "yếu", thường là cây quyết định.
- một mô hình học máy "mạnh", bao gồm nhiều mô hình yếu.
Trong phương pháp tăng cường độ dốc, ở mỗi bước, một mô hình yếu mới được huấn luyện để dự đoán "lỗi" của mô hình mạnh hiện tại (được gọi là phản hồi giả). Chúng ta sẽ trình bày chi tiết về "lỗi" ở phần sau. Hiện tại, giả sử "lỗi" là chênh lệch giữa giá trị dự đoán và nhãn hồi quy. Sau đó, mô hình yếu (tức là "lỗi") được thêm vào mô hình mạnh bằng dấu âm để giảm lỗi của mô hình mạnh.
Phương pháp tăng cường độ dốc là lặp lại. Mỗi lần lặp lại sẽ gọi công thức sau:
\[ F_{i+1} = F_i - f_i \]
trong đó:
- $F_i$ là mô hình mạnh ở bước $i$.
- $f_i$ là mô hình yếu ở bước $i$.
Thao tác này lặp lại cho đến khi đáp ứng một tiêu chí dừng, chẳng hạn như số lần lặp lại tối đa hoặc nếu mô hình (mạnh) bắt đầu phù hợp quá mức khi được đo lường trên một tập dữ liệu xác thực riêng biệt.
Hãy minh hoạ phương pháp tăng cường độ dốc trên một tập dữ liệu hồi quy đơn giản, trong đó:
- Mục tiêu là dự đoán $y$ từ $x$.
- Mô hình mạnh được khởi tạo thành hằng số bằng 0: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Hãy áp dụng mã này cho tập dữ liệu sau:
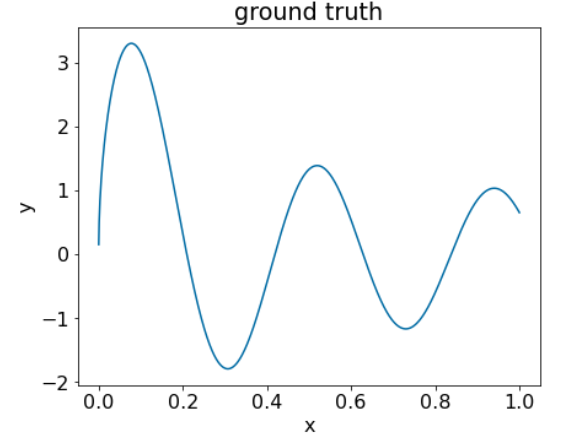
Hình 25. Một tập dữ liệu hồi quy tổng hợp có một đặc điểm số.
Sau đây là 3 biểu đồ sau lần lặp đầu tiên của thuật toán tăng cường độ dốc:
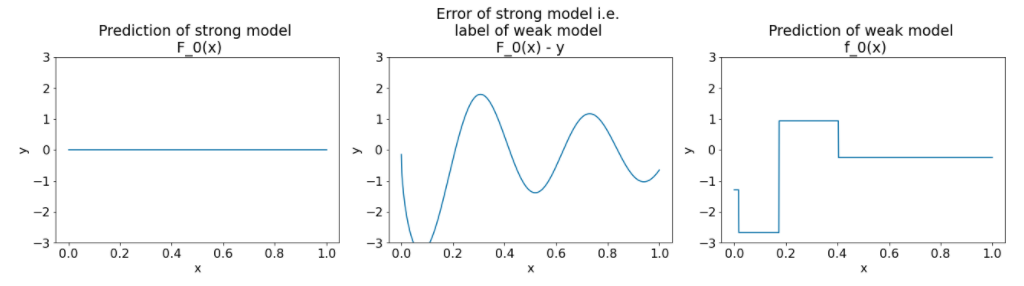
Hình 26. Ba biểu đồ sau lần lặp lại đầu tiên.
Lưu ý những điều sau đây về các biểu đồ trong Hình 26:
- Biểu đồ đầu tiên cho thấy các dự đoán của mô hình mạnh, hiện luôn là 0.
- Biểu đồ thứ hai cho thấy lỗi, là nhãn của mô hình yếu.
- Biểu đồ thứ ba cho thấy mô hình yếu.
Mô hình yếu đầu tiên đang học cách biểu diễn thô của nhãn và chủ yếu tập trung vào phần bên trái của không gian đặc điểm (phần có nhiều biến thể nhất, do đó có nhiều lỗi nhất cho mô hình không ngừng sai).
Dưới đây là các biểu đồ tương tự cho một lần lặp lại khác của thuật toán:
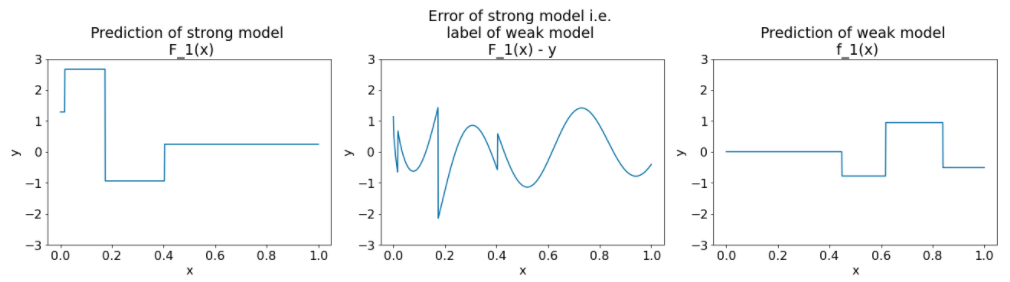
Hình 27. Ba biểu đồ sau lần lặp lại thứ hai.
Lưu ý những điều sau đây về các biểu đồ trong Hình 27:
- Mô hình mạnh hiện chứa dự đoán của mô hình yếu trong lần lặp lại trước.
- Lỗi mới của mô hình mạnh nhỏ hơn một chút.
- Dự đoán mới của mô hình yếu hiện tập trung vào phần bên phải của không gian đặc điểm.
Chúng ta chạy thuật toán này thêm 8 vòng lặp:
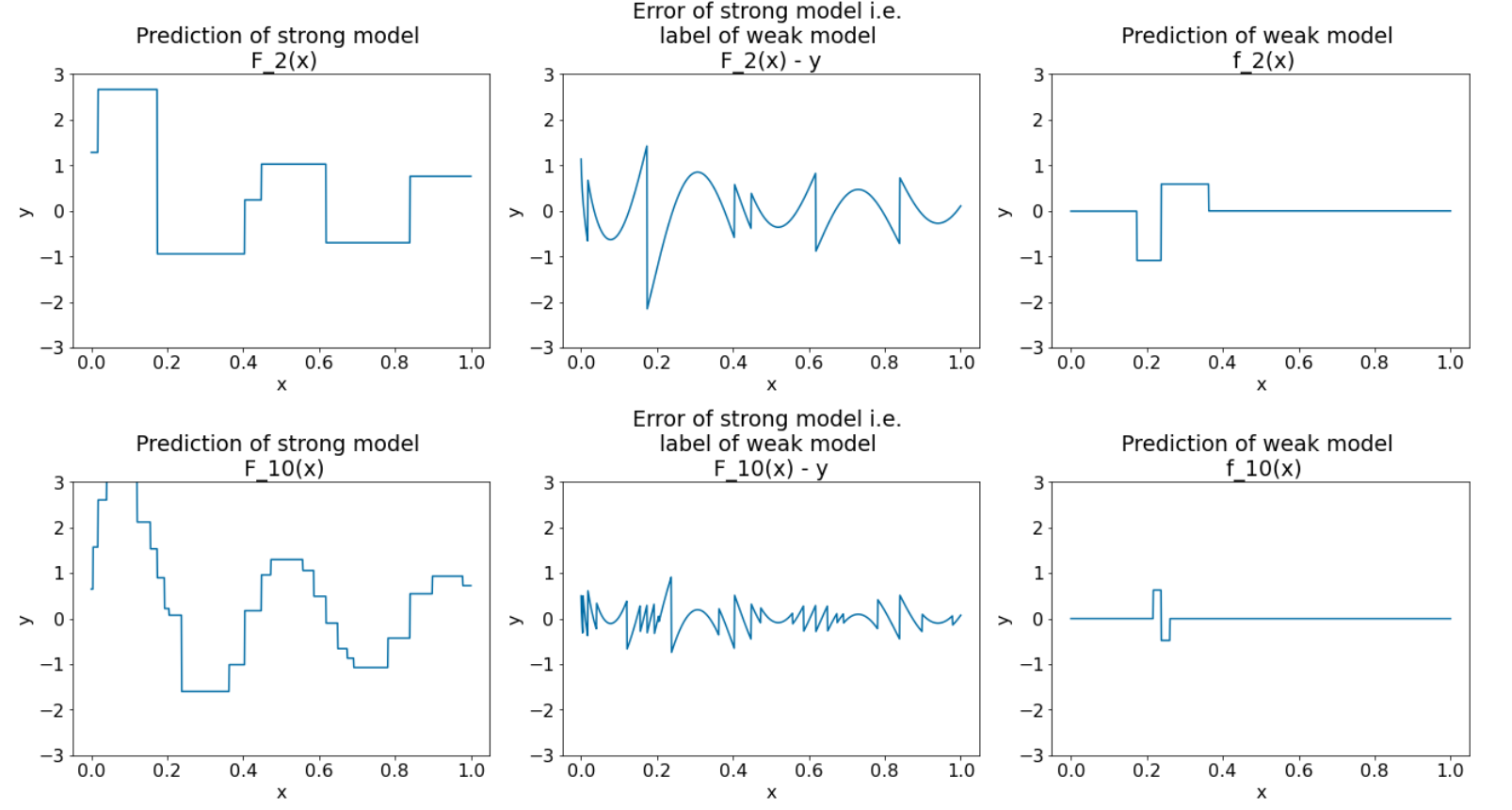
Hình 28. Ba biểu đồ sau lần lặp thứ ba và lần lặp thứ mười.
Trong Hình 28, hãy lưu ý rằng dự đoán của mô hình mạnh bắt đầu giống với biểu đồ của tập dữ liệu.
Những hình này minh hoạ thuật toán tăng cường độ dốc bằng cách sử dụng cây quyết định làm trình học yếu. Cách kết hợp này được gọi là cây tăng cường độ dốc (quyết định).
Các biểu đồ trước đây cho thấy bản chất của phương pháp tăng cường độ dốc. Tuy nhiên, ví dụ này thiếu hai thao tác thực tế sau:
- Sự co rút
- Tối ưu hoá giá trị lá bằng một bước của phương pháp Newton
Sự co rút
Mô hình yếu $f_i$ được nhân với một giá trị nhỏ $\nu$ (ví dụ: $\nu = 0, 1$) trước khi được thêm vào mô hình mạnh $F_i$. Giá trị nhỏ này được gọi là hệ số thu hẹp. Nói cách khác, thay vì mỗi lần lặp lại sử dụng công thức sau:
\[ F_{i+1} = F_i - f_i \]
Mỗi lần lặp lại sử dụng công thức sau:
\[ F_{i+1} = F_i - \nu f_i \]
Sự co rút trong phương pháp tăng cường độ dốc tương tự như tốc độ học trong mạng nơron. Hiệu ứng co rút kiểm soát tốc độ học của mô hình mạnh, giúp hạn chế việc điều chỉnh quá mức. Tức là giá trị co rút gần 0,0 sẽ làm giảm tình trạng phù hợp quá mức nhiều hơn giá trị co rút gần 1,0.
Trong mã ở trên, việc thu hẹp sẽ được triển khai như sau:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
