过拟合和剪枝
使用上述算法,我们可以训练一个决策树,假设样本是可分离的,该决策树将完美地对训练样本进行分类。但是,如果数据集包含噪声,此树将过度拟合数据,并显示较低的测试准确性。
下图显示了一个带噪数据集,其中特征 x 与标签 y 之间存在线性关系。该图还显示了在没有任何正则化的情况下,基于此数据集训练的决策树。此模型正确预测了所有训练示例(模型的预测与训练示例相符)。但是,在包含相同线性模式和不同噪声实例的新数据集上,该模型的效果会很差。
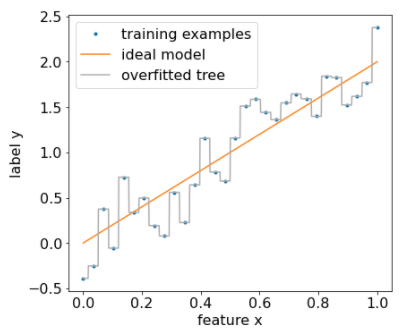
图 12. 包含噪声的数据集。
如需限制决策树过拟合,请在训练决策树时应用以下一种或两种正则化标准:
- 设置深度上限:防止决策树的深度超过上限(例如 10)。
- 设置叶子中的示例数下限:如果叶子中的示例数少于特定数量,则不会考虑对其进行拆分。
下图展示了不同叶子节点的最小示例数的影响。模型捕获的噪声较少。
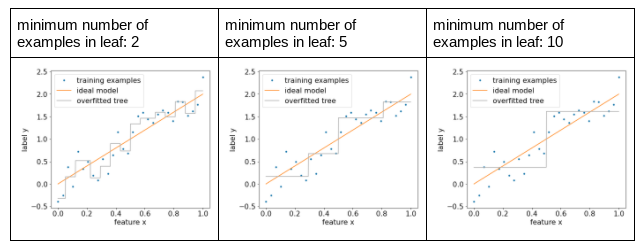
图 13. 每个叶子的最小示例数不同。
您还可以在训练后通过选择性地移除(修剪)某些分支(即将某些非叶节点转换为叶节点)来进行正则化。选择要移除的分支的常见解决方案是使用验证数据集。也就是说,如果移除某个分支可以提高验证数据集上的模型质量,则系统会移除该分支。
下图展示了这一想法。在这里,我们测试如果将非叶绿色节点转换为叶节点(即修剪橙色节点),决策树的验证准确性是否会提高。
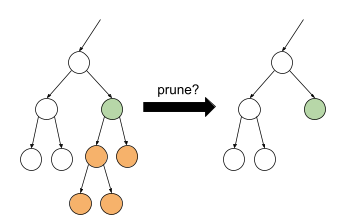
图 14. 将条件及其子项修剪为叶子。
下图展示了使用 20% 的数据集作为验证数据对决策树进行剪枝的效果:
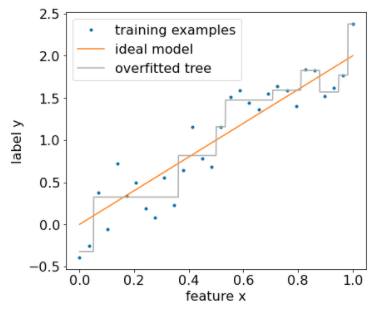
图 15. 使用 20% 的数据集对决策树进行修剪。
请注意,使用验证数据集会减少可用于决策树的初始训练的示例数量。
许多模特创作者会应用多种标准。例如,您可以执行以下所有操作:
- 为每个叶子应用最小示例数。
- 应用最大深度以限制决策树的增长。
- 修剪决策树。
- 示例数量不得少于 5 个 (
min_examples = 5) - 10% 的训练数据集会保留用于验证 (
validation_ratio = 0.1)。
validation_ratio=0.0 来停用对验证数据集的剪枝。
这些标准会引入需要调优的新超参数(例如最大树深),通常会通过自动超参数调优来实现。决策树的训练速度通常足够快,可以使用交叉验证进行超参数调整。例如,对于包含“n”个示例的数据集:
- 将训练示例划分为 p 个不重叠的组。例如:
p=10。 - 针对所有可能的超参数值;例如,最大深度为 {3,5,6,7,8,9},最小示例数为 {5,8,10,20}。
- 针对每个组,评估在其他 p-1 个组上训练的决策树的质量。
- 对各组的评估结果求平均值。
- 选择平均评估值最高的超参数值。
- 使用所选超参数训练包含所有“n”个示例的最终决策树。
在本部分中,我们讨论了决策树限制过拟合的各种方法。尽管有这些方法,但欠拟合和过拟合是决策树的主要弱点。决策树引入了一些新方法来限制过拟合,我们稍后会介绍。
直接决策树解读
决策树易于解读。不过,即使更改几个示例,也可能会完全改变决策树的结构,进而改变对决策树的解读。
由于决策树的构建方式(对训练示例进行划分),因此可以使用决策树来解释数据集本身(而不是模型)。每个叶子都代表数据集的特定角落。
model.describe() 函数查看树。您还可以使用 model.get_tree() 访问和绘制单个树。如需了解详情,请参阅
YDF 的模型检查教程。不过,间接解读也能提供有用的信息。