Overfitting และการตัด
เมื่อใช้อัลกอริทึมที่อธิบายข้างต้น เราสามารถฝึกแผนผังการตัดสินใจที่จะจัดประเภทตัวอย่างการฝึกอย่างสมบูรณ์ได้ ในกรณีที่ตัวอย่างแยกกันได้ อย่างไรก็ตาม หากชุดข้อมูลมีสัญญาณรบกวน ต้นไม้นี้จะปรับให้เข้ากับข้อมูลมากเกินไปและแสดงการทดสอบที่ไม่แม่นยำ
รูปภาพต่อไปนี้แสดงชุดข้อมูลที่มีสัญญาณรบกวนซึ่งมีความสัมพันธ์เชิงเส้นระหว่างฟีเจอร์ x กับป้ายกํากับ y รูปภาพนี้ยังแสดงต้นไม้การตัดสินใจที่ผ่านการฝึกอบรมในชุดข้อมูลนี้โดยไม่มีการปรับสมดุลประเภทใดๆ ด้วย โมเดลนี้คาดการณ์ตัวอย่างการฝึกทั้งหมดได้อย่างถูกต้อง (การคาดการณ์ของโมเดลตรงกับตัวอย่างการฝึก) อย่างไรก็ตาม ในชุดข้อมูลใหม่ที่มีรูปแบบเชิงเส้นเดียวกันและอินสแตนซ์ของสัญญาณรบกวนอื่น โมเดลจะทำงานได้ไม่ดี
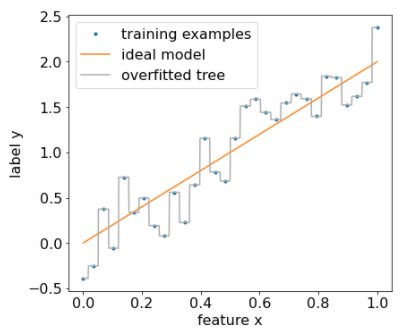
รูปที่ 12 ชุดข้อมูลที่มีสัญญาณรบกวน
หากต้องการจํากัดการพอดีมากเกินไปของแผนผังการตัดสินใจ ให้ใช้เกณฑ์การปรับให้เหมาะสมต่อไปนี้อย่างน้อย 1 ข้อหรือทั้ง 2 ข้อขณะฝึกแผนผังการตัดสินใจ
- กำหนดความลึกสูงสุด: ป้องกันไม่ให้ต้นไม้การตัดสินใจมีลําดับชั้นเกินความลึกสูงสุด เช่น 10
- กำหนดจำนวนตัวอย่างขั้นต่ำในใบ: ระบบจะไม่พิจารณาแยกใบที่มีตัวอย่างน้อยกว่าจำนวนที่กําหนด
รูปภาพต่อไปนี้แสดงผลของจำนวนตัวอย่างขั้นต่ำที่แตกต่างกันต่อใบ โมเดลจะจับเสียงรบกวนน้อยลง
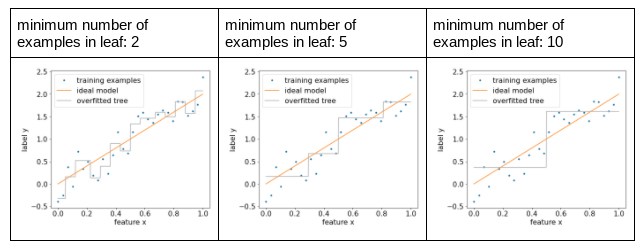
รูปที่ 13 จำนวนตัวอย่างขั้นต่ำที่แตกต่างกันต่อใบ
นอกจากนี้ คุณยังทำให้เป็นปกติได้หลังจากการฝึกโดยเลือกนำ (ตัด) กิ่งบางกิ่งออก กล่าวคือ แปลงโหนดที่ไม่ใช่ใบเป็นใบ วิธีที่พบบ่อยในการเลือกสาขาที่จะนําออกคือการใช้ชุดข้อมูลที่ใช้ตรวจสอบ กล่าวคือ หากการนำสาขาออกช่วยปรับปรุงคุณภาพของโมเดลในชุดข้อมูลที่ใช้ตรวจสอบ ทางระบบก็จะนำสาขานั้นออก
ภาพต่อไปนี้แสดงแนวคิดนี้ ในส่วนนี้ เราจะทดสอบว่าความแม่นยำของการตรวจสอบต้นไม้การตัดสินใจจะดีขึ้นไหมหากเปลี่ยนโหนดสีเขียวที่ไม่ใช่ใบไม้ให้กลายเป็นใบไม้ นั่นคือ การตัดโหนดสีส้มออก
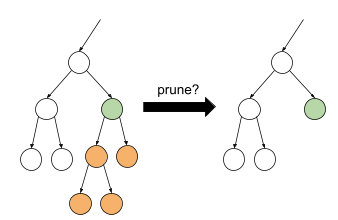
รูปที่ 14 การตัดเงื่อนไขและเงื่อนไขย่อยให้เป็นใบ
รูปภาพต่อไปนี้แสดงผลของการใช้ชุดข้อมูล 20% เป็นข้อมูลตรวจสอบเพื่อตัดแต่งแผนผังการตัดสินใจ
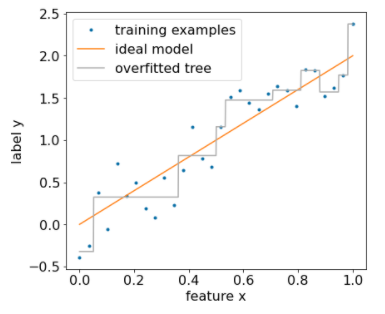
รูปที่ 15 ใช้ 20% ของชุดข้อมูลเพื่อตัดแต่งแผนผังการตัดสินใจ
โปรดทราบว่าการใช้ชุดข้อมูลที่ใช้ตรวจสอบจะลดจํานวนตัวอย่างที่ใช้ได้สําหรับการฝึกต้นไม้การตัดสินใจครั้งแรก
ครีเอเตอร์โมเดลหลายคนใช้เกณฑ์หลายรายการ ตัวอย่างเช่น คุณอาจทำสิ่งต่อไปนี้ทั้งหมด
- ใช้จำนวนตัวอย่างขั้นต่ำต่อใบ
- ใช้ความลึกสูงสุดเพื่อจํากัดการเติบโตของแผนผังการตัดสินใจ
- ตัดแต่งแผนผังการตัดสินใจ
- จำนวนตัวอย่างขั้นต่ำคือ 5 (
min_examples = 5) - ระบบจะเก็บชุดข้อมูลการฝึก 10% ไว้สําหรับการตรวจสอบ (
validation_ratio = 0.1)
validation_ratio=0.0
เกณฑ์เหล่านี้จะแนะนำไฮเปอร์พารามิเตอร์ใหม่ที่ต้องปรับแต่ง (เช่น ความลึกของต้นไม้สูงสุด) ซึ่งมักจะมาพร้อมกับการปรับแต่งไฮเปอร์พารามิเตอร์อัตโนมัติ โดยทั่วไปแล้ว ต้นไม้การตัดสินใจจะฝึกให้ใช้การปรับพารามิเตอร์ส่วนกลางด้วยการตรวจสอบไขว้ได้เร็วพอ เช่น ในชุดข้อมูลที่มีตัวอย่าง "n" รายการ
- แบ่งตัวอย่างการฝึกออกเป็น p กลุ่มที่ไม่ทับซ้อนกัน ตัวอย่างเช่น
p=10 - สำหรับค่าไฮเปอร์พารามิเตอร์ที่เป็นไปได้ทั้งหมด เช่น ความลึกสูงสุดใน {3,5,6,7,8,9} ตัวอย่างขั้นต่ำใน {5,8,10,20}
- ประเมินคุณภาพของต้นไม้การตัดสินใจที่ผ่านการฝึกอบรมในกลุ่ม p-1 กลุ่มอื่นๆ ในแต่ละกลุ่ม
- หาค่าเฉลี่ยของการประเมินในกลุ่ม
- เลือกค่าไฮเปอร์พารามิเตอร์ที่มีการประเมินโดยเฉลี่ยที่ดีที่สุด
- ฝึกแผนผังการตัดสินใจขั้นสุดท้ายโดยใช้ตัวอย่าง "n" รายการทั้งหมดด้วยไฮเปอร์พารามิเตอร์ที่เลือก
ในส่วนนี้ เราจะพูดถึงวิธีต่างๆ ที่ต้นไม้การตัดสินใจจํากัดการพอดีมากเกินไป แม้จะมีวิธีการเหล่านี้ แต่การประมาณที่น้อยเกินไปและการประมาณที่มากเกินไปก็ยังคงเป็นจุดอ่อนหลักของต้นไม้การตัดสินใจ ป่าการตัดสินใจจะแนะนำวิธีการใหม่ในการจำกัดการพอดีมากเกินไป ซึ่งเราจะได้ดูในภายหลัง
การตีความแผนผังการตัดสินใจโดยตรง
แผนภูมิการตัดสินใจตีความได้ง่าย อย่างไรก็ตาม การเปลี่ยนแปลงตัวอย่างเพียงไม่กี่รายการอาจเปลี่ยนโครงสร้างและวิธีตีความของแผนภูมิการตัดสินใจไปอย่างสิ้นเชิง
เนื่องจากวิธีการสร้างแผนภูมิการตัดสินใจและการแบ่งกลุ่มตัวอย่างการฝึก ทำให้สามารถใช้แผนภูมิการตัดสินใจเพื่อตีความชุดข้อมูลได้ (แทนที่จะใช้กับโมเดล) ใบแต่ละใบแสดงถึงมุมหนึ่งๆ ของชุดข้อมูล
model.describe()
นอกจากนี้ คุณยังเข้าถึงและพล็อตต้นไม้แต่ละต้นด้วย model.get_tree() ได้ด้วย
ดูรายละเอียดเพิ่มเติมได้ที่
บทแนะนำการตรวจสอบโมเดลของ YDF
อย่างไรก็ตาม การตีความโดยอ้อมก็ให้ข้อมูลด้วยเช่นกัน