Ao contrário das florestas aleatórias, as árvores otimizadas com gradiente podem se ajustar demais. Portanto, para redes neurais, é possível aplicar a regularização e a interrupção antecipada usando um conjunto de dados de validação.
Por exemplo, as figuras a seguir mostram curvas de perda e precisão para conjuntos de treinamento e validação ao treinar um modelo de GBT. Observe como as curvas são divergentes, o que sugere um alto grau de ajuste excessivo.
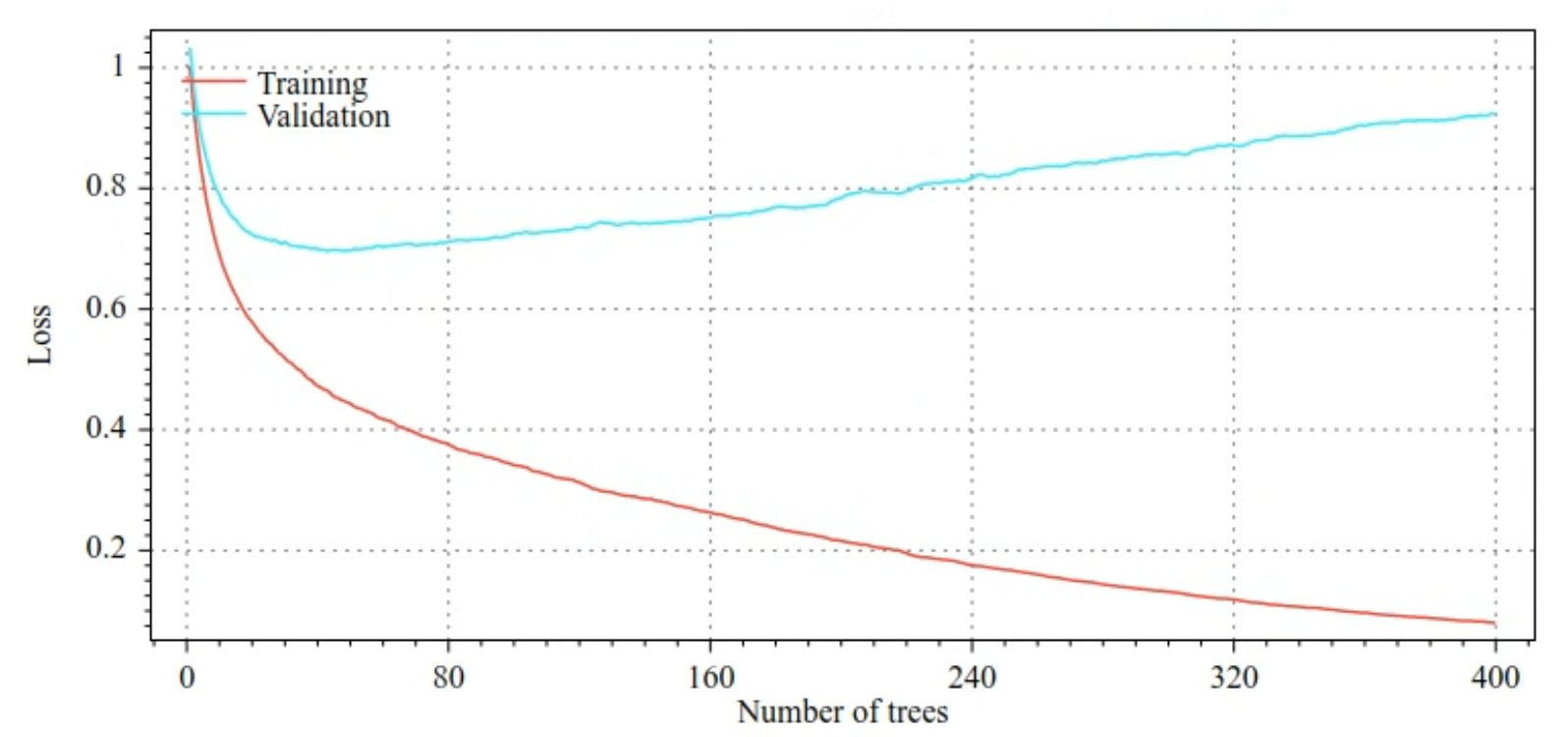
Figura 29. Perda x número de árvores de decisão.
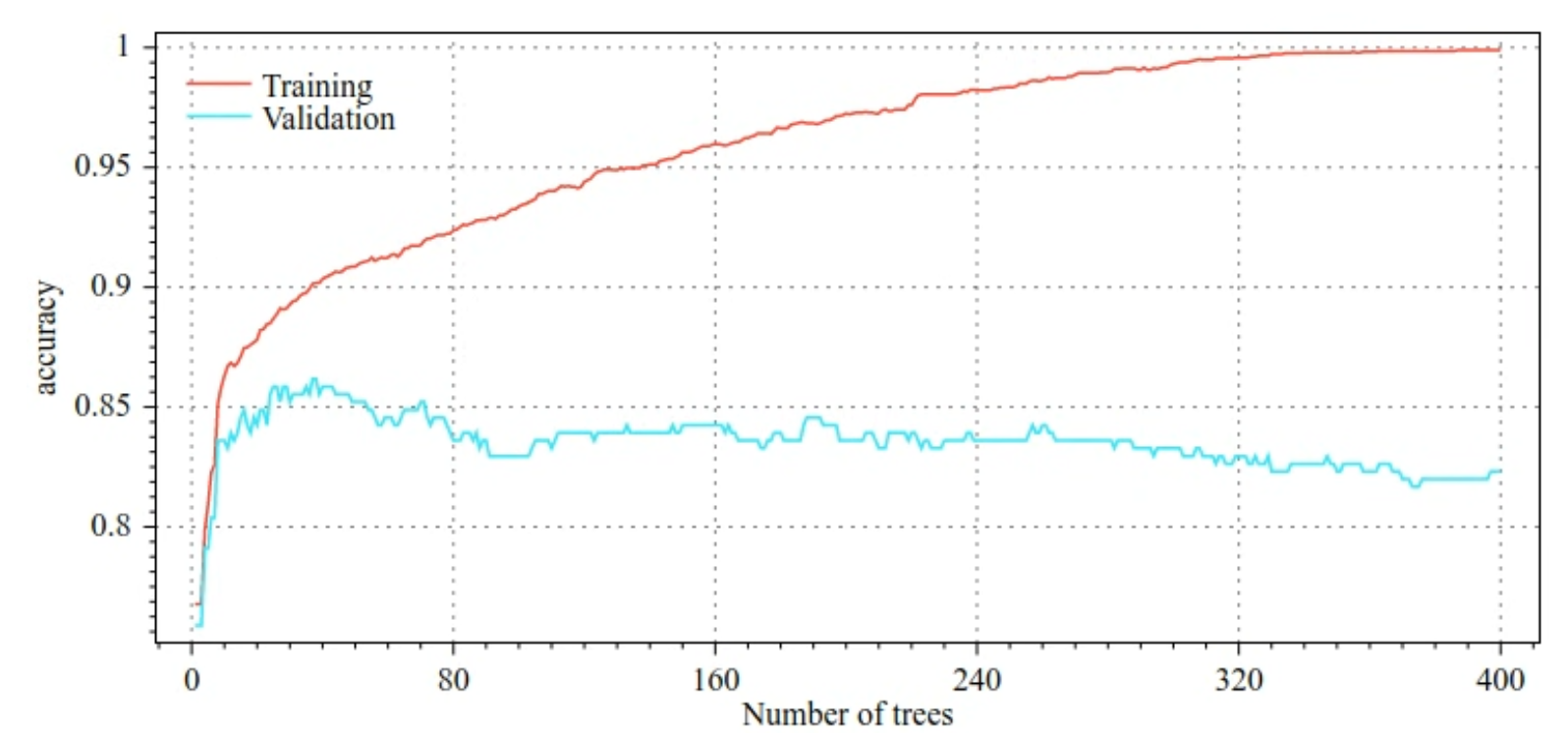
Figura 30. Precisão x número de árvores de decisão.
Os parâmetros de regularização comuns para árvores impulsionadas por gradiente incluem:
- A profundidade máxima da árvore.
- A taxa de encolhimento.
- A proporção de atributos testados em cada nó.
- Coeficientes L1 e L2 na perda.
As árvores de decisão geralmente são muito mais rasas do que os modelos de florestas aleatórias. Por padrão, as árvores de gradiente aprimoradas no TF-DF são desenvolvidas até a profundidade 6. Como as árvores são rasas, o número mínimo de exemplos por folha tem pouco impacto e geralmente não é ajustado.
A necessidade de um conjunto de dados de validação é um problema quando o número de exemplos de treinamento é pequeno. Portanto, é comum treinar árvores de gradiente impulsionado em um loop de validação cruzada ou desativar a interrupção antecipada quando o modelo não tiver overfitting.
Exemplo de uso
No capítulo anterior, treinamos uma floresta aleatória em um pequeno conjunto de dados. Neste exemplo, vamos simplesmente substituir o modelo de floresta aleatória por um modelo de árvores otimizadas com gradiente:
model = tfdf.keras.GradientBoostedTreesModel()
# Part of the training dataset will be used as validation (and removed
# from training).
model.fit(tf_train_dataset)
# The user provides the validation dataset.
model.fit(tf_train_dataset, validation_data=tf_valid_dataset)
# Disable early stopping and the validation dataset. All the examples are
# used for training.
model.fit(
tf_train_dataset,
validation_ratio=0.0,
early_stopping="NONE")
# Note: When "validation_ratio=0", early stopping is automatically disabled,
# so early_stopping="NONE" is redundant here.
Uso e limitações
As árvores com aprimoramento por gradiente têm algumas vantagens e desvantagens.
Vantagens
- Assim como as árvores de decisão, elas oferecem suporte nativo a atributos numéricos e categóricos e, muitas vezes, não precisam de pré-processamento de atributos.
- As árvores de gradiente otimizadas têm hiperparâmetros padrão que geralmente geram ótimos resultados. No entanto, o ajuste desses hiperparâmetros pode melhorar significativamente o modelo.
- Os modelos de árvore com reforço de gradiente geralmente são pequenos (em número de nós e em memória) e rápidos para executar (geralmente apenas um ou alguns µs / exemplos).
Desvantagens
- As árvores de decisão precisam ser treinadas sequencialmente, o que pode desacelerar o treinamento consideravelmente. No entanto, a desaceleração do treinamento é compensada pelas árvores de decisão menores.
- Assim como as florestas aleatórias, as árvores com escalonamento gradual não podem aprender e reutilizar representações internas. Cada árvore de decisão (e cada ramo dela) precisa reaprender o padrão do conjunto de dados. Em alguns conjuntos de dados, principalmente aqueles com dados não estruturados (por exemplo, imagens, texto), isso faz com que as árvores impulsionadas por gradiente mostrem resultados piores do que outros métodos.
