Случайные леса

Случайный лес ( RF ) — это ансамбль деревьев решений, в котором каждое дерево решений обучается с использованием определенного случайного шума. Случайные леса — самая популярная форма ансамбля деревьев решений. В этом модуле обсуждаются несколько методов создания независимых деревьев решений, позволяющих повысить вероятность построения эффективного случайного леса.

Упаковка

Бэггинг ( бутстрап - агрегирование ) означает обучение каждого дерева решений на случайном подмножестве примеров в обучающем наборе. Другими словами, каждое дерево решений в случайном лесу обучается на различном подмножестве примеров.

Упаковка своеобразная. Каждое дерево решений обучается на том же количестве примеров, что и в исходном обучающем наборе. Например, если исходный обучающий набор содержит 60 примеров, то каждое дерево решений обучается на 60 примерах. Однако при пакетировании каждое дерево решений обучается только на подмножестве (обычно 67%) этих примеров. Таким образом, некоторые из этих 40 примеров в подмножестве необходимо повторно использовать при обучении данного дерева решений. Такое повторное использование называется обучением «с заменой».

Например, в Таблице 6 показано, как пакетирование может распределить шесть примеров по трем деревьям решений. Обратите внимание на следующее:

• Каждое дерево решений обучается на шести примерах.
• Каждое дерево решений обучается на своем наборе примеров.
• Каждое дерево решений повторно использует определенные примеры. Например, пример № 4 используется дважды в дереве решений обучения 1; следовательно, изученный вес примера № 4 фактически удваивается в дереве решений 1.

Таблица 6. Объединение шести обучающих примеров в три дерева решений. Каждое число представляет собой количество повторений данного обучающего примера (№ 1–6) в наборе обучающих данных данного дерева решений (1–3).

	примеры обучения
	№1	#2	#3	#4	#5	#6
исходный набор данных	1	1	1	1	1	1
дерево решений 1	1	1	0	2	1	1
дерево решений 2	3	0	1	0	2	0
дерево решений 3	0	1	3	1	0	1

При пакетировании каждое дерево решений почти всегда обучается на общем количестве примеров в исходном обучающем наборе. Обучение каждого дерева решений на большем или меньшем количестве примеров приводит к ухудшению качества случайного леса.

Выборка примеров, хотя и не присутствует в исходной статье о случайном лесу , иногда выполняется «без замены»; то есть обучающий пример не может присутствовать в обучающем наборе дерева решений более одного раза. Например, в предыдущей таблице все значения будут либо 0, либо 1.

Код YDF

Вы можете включить обучение без замены, выполнив следующее назначение в YDF: bootstrap_training_dataset=False

Выборка атрибутов

Выборка атрибутов означает, что вместо поиска наилучшего состояния среди всех доступных функций на каждом узле проверяется только случайное подмножество функций. Набор тестируемых функций выбирается случайным образом в каждом узле дерева решений.

Следующее дерево решений иллюстрирует выборку атрибутов/признаков. Здесь дерево решений обучается на 5 признаках (f1-f5). Синие узлы представляют протестированные функции, а белые — непроверенные. Условие построено на основе лучших протестированных функций (отмечено красным контуром).

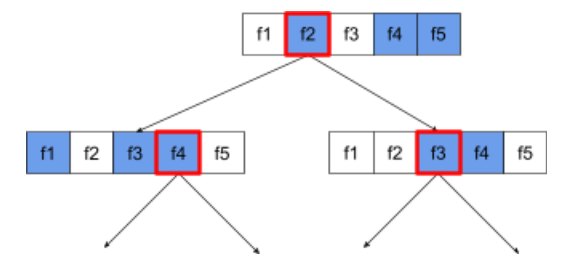
Рисунок 21. Выборка атрибутов.

Коэффициент выборки атрибутов является важным гиперпараметром регуляризации. На предыдущем рисунке использовалось соотношение ~⅗. Многие реализации случайного леса по умолчанию проверяют 1/3 признаков для регрессии и sqrt (количество признаков) для классификации.

В TF-DF выборкой атрибутов управляют следующие гиперпараметры:

• num_candidate_attributes
• num_candidate_attributes_ratio

Например, если num_candidate_attributes_ratio=0.5 , половина функций будет проверена на каждом узле.

Отключение регуляризации дерева решений

Отдельные деревья решений в случайном лесу обучаются без обрезки. (См. Переобучение и обрезка ). Это приводит к созданию слишком сложных деревьев с плохим качеством прогнозирования. Вместо регуляризации отдельных деревьев деревья объединяются в ансамбль, что дает более точные общие прогнозы.

Примечание. Часто резкое уменьшение дисперсии отдельных деревьев решений (например, путем ограничения их глубины) улучшает качество прогнозирования отдельных деревьев решений, но ухудшает точность прогнозирования случайного леса.

Мы ожидаем, что точность обучения и тестирования случайного леса будет различаться. Точность обучения случайного леса обычно намного выше (иногда равна 100%). Однако очень высокая точность обучения в случайном лесу является нормальной и не означает, что случайный лес переобучен.

Два источника случайности (пакетирование и выборка по атрибутам) обеспечивают относительную независимость между деревьями решений. Эта независимость корректирует переоснащение отдельных деревьев решений. Следовательно, ансамбль не переоснащен. Мы проиллюстрируем этот неинтуитивный эффект в следующем разделе.

Чисто случайные леса обучаются без максимальной глубины или минимального количества наблюдений на лист. На практике полезно ограничить максимальную глубину и минимальное количество наблюдений на лист. По умолчанию многие случайные леса используют следующие значения по умолчанию:

• максимальная глубина ~16
• минимальное количество наблюдений на лист ~5.

Вы можете настроить эти гиперпараметры.

Код YDF

Тюнер YDF — это простой способ настройки гиперпараметров. Дополнительную информацию см. в руководстве по настройке YDF .

Четкость шума

Почему случайный шум может улучшить качество случайного леса? Чтобы проиллюстрировать преимущества случайного шума, на рисунке 22 показаны прогнозы классического (обрезанного) дерева решений и случайного леса, обученного на нескольких примерах простой двумерной задачи с эллиптической структурой.

Шаблоны эллипсов, как известно, сложны для изучения алгоритмами дерева решений и леса решений с условиями, выровненными по оси, поэтому они служат хорошим примером. Обратите внимание, что сокращенное дерево решений не может обеспечить того же качества прогнозирования, что и случайный лес.

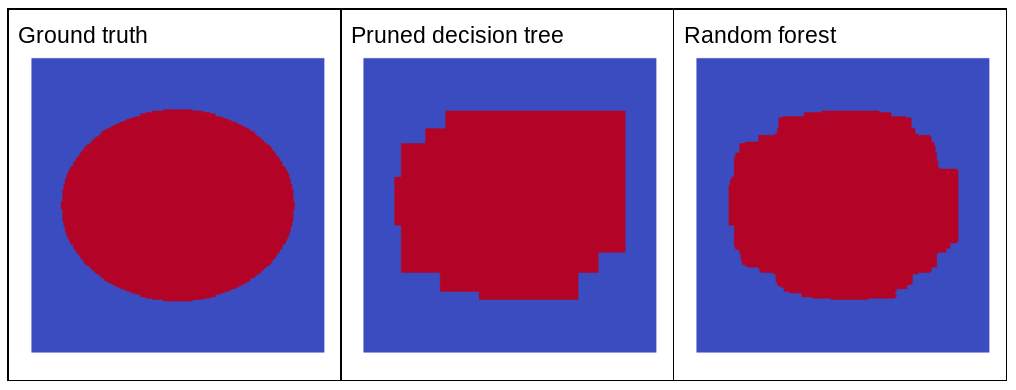
Рисунок 22. Основная истина и прогнозы, сгенерированные одним сокращенным деревом решений, и прогнозы, сгенерированные случайным лесом.

Следующий график показывает предсказания первых трех необрезанных деревьев решений случайного леса; то есть все деревья решений обучаются с использованием комбинации:

• упаковка в мешки
• выборка атрибутов
• отключение обрезки

Обратите внимание, что отдельные прогнозы этих трех деревьев решений хуже , чем прогнозы сокращенного дерева решений на предыдущем рисунке. Однако, поскольку ошибки отдельных деревьев решений слабо коррелируют, три дерева решений объединяются в ансамбль для создания эффективных прогнозов.

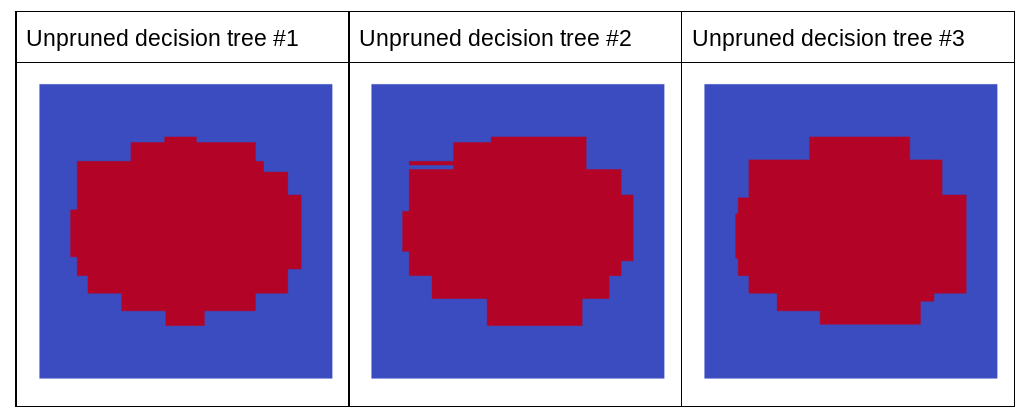
Рисунок 23. Три необрезанных дерева решений, которые построят эффективный ансамбль.

Поскольку деревья решений случайного леса не обрезаются, обучение случайного леса не требует набора проверочных данных. На практике, особенно на небольших наборах данных, модели следует обучать на всех доступных данных.

При обучении случайного леса по мере добавления большего количества деревьев решений ошибка почти всегда уменьшается; то есть качество модели почти всегда улучшается. Да, добавление большего количества деревьев решений почти всегда уменьшает ошибку случайного леса. Другими словами, добавление большего количества деревьев решений не может привести к переобучению случайного леса. В какой-то момент модель просто перестает улучшаться. Лео Брейман как-то сказал: « Случайные леса не переопределяются, если добавить больше деревьев ».

Например, на следующем графике показана тестовая оценка модели случайного леса при добавлении большего количества деревьев решений. Точность быстро повышается, пока не достигает значения около 0,865. Однако добавление большего количества деревьев решений не снижает точность; другими словами, модель не переобучается. Такое поведение (в основном) всегда верно и независимо от гиперпараметров.

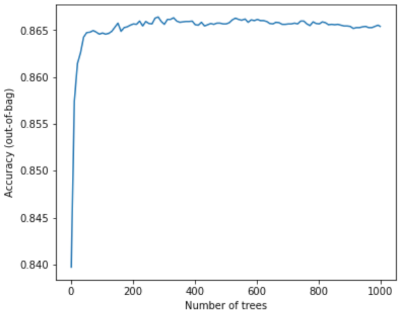
Рисунок 24. Точность остается постоянной по мере добавления в случайный лес новых деревьев решений.