랜덤 포레스트
무작위 포레스트 (RF)는 각 결정 트리가 특정 무작위 노이즈로 학습되는 결정 트리의 앙상블입니다. 랜덤 포레스트는 가장 인기 있는 결정 트리 앙상블 형태입니다. 이 단원에서는 효과적인 무작위 포레스트 빌드 가능성을 높이기 위해 독립적인 결정 트리를 만드는 몇 가지 기술을 설명합니다.
bagging
Bagging (bootstrap aggregating)은 학습 세트의 예 중 무작위 하위 집합에서 각 결정 트리를 학습하는 것을 의미합니다. 즉, 랜덤 포레스트의 각 결정 트리는 다른 하위 집합의 예시를 사용하여 학습됩니다.
bagging은 독특합니다. 각 결정 트리는 원래 학습 세트와 동일한 개수의 예시로 학습됩니다. 예를 들어 원래 학습 세트에 60개의 예시가 포함되어 있으면 각 결정 트리는 60개의 예시로 학습됩니다. 하지만 bagging은 이러한 예시의 하위 집합 (일반적으로 67%)에서만 각 결정 트리를 학습합니다. 따라서 하위 집합의 40개 예시 중 일부는 특정 결정 트리를 학습하는 동안 재사용해야 합니다. 이러한 재사용을 '대체가 있는' 학습이라고 합니다.
예를 들어 표 6은 bagging이 3개의 결정 트리에 6개의 예시를 배포하는 방법을 보여줍니다. 다음 사항에 유의하세요.
- 각 결정 트리는 총 6개의 예시를 사용하여 학습합니다.
- 각 결정 트리는 서로 다른 예시 집합으로 학습합니다.
- 각 결정 트리는 특정 예시를 재사용합니다. 예를 들어 예 4는 학습 결정 트리 1에서 두 번 사용됩니다. 따라서 예 4의 학습된 가중치는 결정 트리 1에서 효과적으로 두 배가 됩니다.
표 6. 세 개의 결정 트리에서 6개의 학습 예시를 bagging합니다. 각 숫자는 특정 결정 트리(1~3)의 학습 데이터 세트에서 특정 학습 예시(#1~6)가 반복되는 횟수를 나타냅니다.
| 학습 예시 | ||||||
|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | |
| 원본 데이터 세트 | 1 | 1 | 1 | 1 | 1 | 1 |
| 결정 트리 1 | 1 | 1 | 0 | 2 | 1 | 1 |
| 결정 트리 2 | 3 | 0 | 1 | 0 | 2 | 0 |
| 결정 트리 3 | 0 | 1 | 3 | 1 | 0 | 1 |
bagging에서는 각 결정 트리가 거의 항상 원래 학습 세트의 총 예시 수를 사용하여 학습됩니다. 예시가 더 많거나 더 적은 경우 각 결정 트리를 학습하면 랜덤 포레스트의 품질이 저하되는 경향이 있습니다.
원래 랜덤 포레스트 논문에는 없지만, 예시 샘플링은 '교체 없이' 실행되는 경우가 있습니다. 즉, 학습 예시는 결정 트리 학습 세트에 두 번 이상 포함될 수 없습니다. 예를 들어 위의 표에서 모든 값은 모두 0 또는 1입니다.
bootstrap_training_dataset=False
속성 샘플링
속성 샘플링은 사용 가능한 모든 기능에서 최적의 조건을 찾는 대신 각 노드에서 무작위로 선택한 일부 기능만 테스트한다는 것을 의미합니다. 테스트된 특성 세트는 결정 트리의 각 노드에서 무작위로 샘플링됩니다.
다음 결정 트리는 속성 / 기능 샘플링을 보여줍니다. 여기서 결정 트리는 5가지 특성 (f1~f5)을 기반으로 학습됩니다. 파란색 노드는 테스트된 기능을 나타내고 흰색 노드는 테스트되지 않은 기능을 나타냅니다. 조건은 가장 많이 테스트된 기능 (빨간색 윤곽선으로 표시됨)으로 구성됩니다.
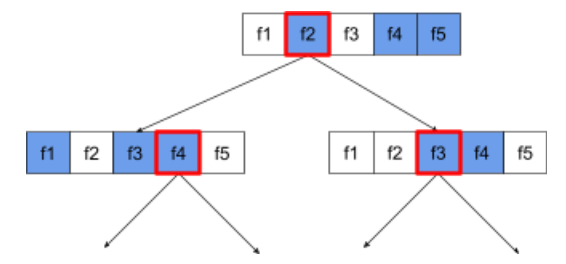
그림 21. 속성 샘플링
속성 샘플링의 비율은 중요한 정규화 하이퍼파라미터입니다. 위 그림에서는 약 ⅗ 비율을 사용했습니다. 많은 랜덤 포레스트 구현은 기본적으로 회귀의 경우 특성의 1/3을, 분류의 경우 sqrt(특성 수)를 테스트합니다.
TF-DF에서 다음 하이퍼파라미터는 속성 샘플링을 제어합니다.
num_candidate_attributesnum_candidate_attributes_ratio
예를 들어 num_candidate_attributes_ratio=0.5이면 각 노드에서 기능의 절반이 테스트됩니다.
결정 트리 정규화 사용 중지
랜덤 포레스트의 개별 결정 트리는 가지치기 없이 학습됩니다. (오버피팅 및 프루닝 참고) 이렇게 하면 예측 품질이 좋지 않은 지나치게 복잡한 트리가 생성됩니다. 개별 트리를 정규화하는 대신 트리를 앙상블하여 더 정확한 전반적인 예측을 생성합니다.
랜덤 포레스트의 학습 정확도와 테스트 정확도는 다를 수 있습니다. 랜덤 포레스트의 학습 정확성은 일반적으로 훨씬 높습니다 (100%인 경우도 있음). 하지만 랜덤 포레스트의 학습 정확성이 매우 높은 것은 정상이며 랜덤 포레스트가 오버핏되었다는 것을 나타내지 않습니다.
두 가지 무작위 소스 (백깅 및 속성 샘플링)는 결정 트리 간의 상대적 독립성을 보장합니다. 이러한 독립성은 개별 결정 트리의 오버피팅을 수정합니다. 따라서 전체 집합이 오버핏되지 않습니다. 다음 단원에서는 직관적이지 않은 이 효과를 설명합니다.
순수 무작위 포리스트는 최대 깊이 또는 리프당 최소 관측 횟수 없이 학습합니다. 실제로는 리프당 최대 깊이와 최소 관측 수를 제한하는 것이 좋습니다. 기본적으로 많은 랜덤 포리스트는 다음과 같은 기본값을 사용합니다.
- 최대 깊이: 약 16
- 리프당 최소 관측치 수는 약 5개입니다.
이러한 초매개변수를 조정할 수 있습니다.
노이즈의 선명도
무작위 노이즈가 랜덤 포레스트의 품질을 개선하는 이유는 무엇인가요? 무작위 노이즈의 이점을 보여주기 위해 그림 22에서는 타원형 패턴이 있는 간단한 2차원 문제의 몇 가지 예시를 바탕으로 학습된 기존(정리된) 결정 트리와 랜덤 포레스트의 예측을 보여줍니다.
타원 패턴은 결정 트리 및 결정 포레스트 알고리즘이 축에 정렬된 조건으로 학습하기가 매우 어렵기 때문에 좋은 예입니다. 정리된 결정 트리는 랜덤 포레스트와 동일한 예측 품질을 얻을 수 없습니다.
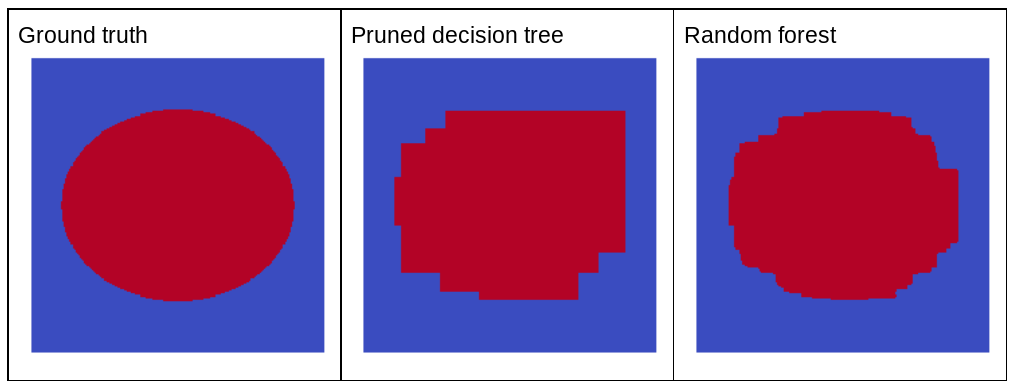
그림 22. 정답과 단일로 프루닝된 결정 트리에서 생성된 예측, 그리고 랜덤 포레스트에서 생성된 예측을 비교합니다.
다음 플롯은 랜덤 포레스트의 가지치기되지 않은 처음 세 개의 결정 트리의 예측을 보여줍니다. 즉, 결정 트리는 다음의 조합으로 모두 학습됩니다.
- bagging
- 속성 샘플링
- 가지치기 사용 중지
이 세 가지 결정 트리의 개별 예측은 앞의 그림에서 자른 결정 트리의 예측보다 나쁩니다. 그러나 개별 결정 트리의 오류는 상관성이 약하므로 세 개의 결정 트리를 앙상블로 결합하여 효과적인 예측을 생성합니다.
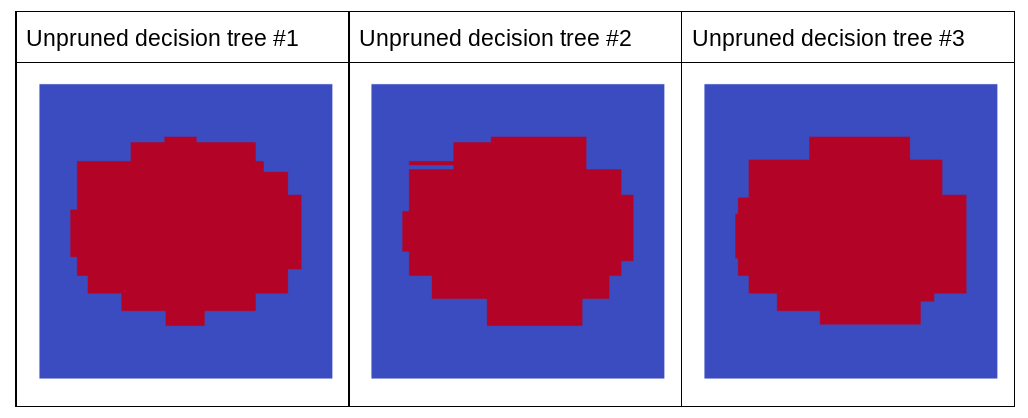
그림 23. 효과적인 앙상블을 구축할 수 있는 가지치기되지 않은 결정 트리 3개
랜덤 포레스트의 결정 트리는 프루닝되지 않으므로 랜덤 포레스트 학습에는 검증 데이터 세트가 필요하지 않습니다. 실제로는 특히 소규모 데이터 세트의 경우 사용 가능한 모든 데이터로 모델을 학습해야 합니다.
랜덤 포레스트 학습 시 결정 트리를 추가할수록 오류가 거의 항상 감소합니다. 즉, 모델 품질이 거의 항상 개선됩니다. 예. 결정 트리를 더 추가하면 거의 항상 랜덤 포레스트의 오류가 줄어듭니다. 즉, 결정 트리를 더 추가해도 랜덤 포레스트가 오버핏되지 않습니다. 어느 시점에서는 모델의 개선이 중단됩니다. 레오 브레이먼은 '랜덤 포레스트는 트리를 더 추가해도 오버핏되지 않습니다'라고 말한 것으로 유명합니다.
예를 들어 다음 플롯은 결정 트리를 더 추가할 때의 랜덤 포레스트 모델 테스트 평가를 보여줍니다. 정확도는 0.865에서 정체될 때까지 빠르게 개선됩니다. 하지만 결정 트리를 더 추가해도 정확도가 떨어지지 않습니다. 즉, 모델이 오버핏되지 않습니다. 이 동작은 대부분 항상 true이며 하이퍼파라미터와 무관합니다.
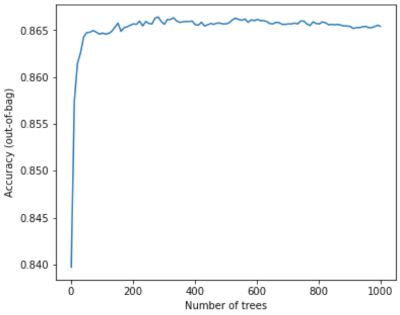
그림 24. 결정 트리가 무작위 포레스트로 추가되더라도 정확성은 일정하게 유지됩니다.