Bosques aleatorios
Un bosque aleatorio (RF) es un conjunto de árboles de decisión en el que cada árbol se entrena con un ruido aleatorio específico. Los bosques aleatorios son la forma más popular de conjunto de árboles de decisión. En esta unidad, se analizan varias técnicas para crear árboles de decisión independientes que mejoren las probabilidades de crear un bosque aleatorio eficaz.
Bagging
Bagging (bootstrap aggregating) significa entrenar cada árbol de decisión en un subconjunto aleatorio de los ejemplos del conjunto de entrenamiento. En otras palabras, cada árbol de decisión del bosque aleatorio se entrena en un subconjunto diferente de ejemplos.
El empaquetado es peculiar. Cada árbol de decisión se entrena con la misma cantidad de ejemplos que en el conjunto de entrenamiento original. Por ejemplo, si el conjunto de entrenamiento original contiene 60 ejemplos, cada árbol de decisión se entrena con 60 ejemplos. Sin embargo, el bagging solo entrena cada árbol de decisión en un subconjunto (por lo general, el 67%) de esos ejemplos. Por lo tanto, algunos de esos 40 ejemplos del subconjunto se deben volver a usar mientras se entrena un árbol de decisión determinado. Esta reutilización se denomina entrenamiento “con reemplazo”.
Por ejemplo, la tabla 6 muestra cómo el bagging podría distribuir seis ejemplos entre tres árboles de decisión. Observa lo siguiente:
- Cada árbol de decisión se entrena en un total de seis ejemplos.
- Cada árbol de decisión se entrena en un conjunto diferente de ejemplos.
- Cada árbol de decisión reutiliza ciertos ejemplos. Por ejemplo, el ejemplo 4 se usa dos veces en el entrenamiento del árbol de decisión 1. Por lo tanto, el peso aprendido del ejemplo 4 se duplica de manera efectiva en el árbol de decisión 1.
Tabla 6. Bagging de seis ejemplos de entrenamiento en tres árboles de decisión. Cada número representa la cantidad de veces que se repite un ejemplo de entrenamiento determinado (<br>#1-6) en el conjunto de datos de entrenamiento de un árbol de decisión determinado (<br>1-3).
| Ejemplos de entrenamiento | ||||||
|---|---|---|---|---|---|---|
| #1 | #2 | N.º 3 | #4 | #5 | #6 | |
| conjunto de datos original | 1 | 1 | 1 | 1 | 1 | 1 |
| árbol de decisión 1 | 1 | 1 | 0 | 2 | 1 | 1 |
| árbol de decisión 2 | 3 | 0 | 1 | 0 | 2 | 0 |
| Árbol de decisión 3 | 0 | 1 | 3 | 1 | 0 | 1 |
En el bagging, cada árbol de decisión casi siempre se entrena con la cantidad total de ejemplos del conjunto de entrenamiento original. El entrenamiento de cada árbol de decisión con más o menos ejemplos suele degradar la calidad del bosque aleatorio.
Si bien no está presente en el artículo original sobre bosques aleatorios, el muestreo de ejemplos a veces se realiza “sin reemplazo”, es decir, un ejemplo de entrenamiento no puede estar presente más de una vez en un conjunto de entrenamiento de árboles de decisión. Por ejemplo, en la tabla anterior, todos los valores serían 0 o 1.
bootstrap_training_dataset=False
Muestreo de atributos
El muestreo de atributos significa que, en lugar de buscar la mejor condición en todas las funciones disponibles, solo se prueba un subconjunto aleatorio de funciones en cada nodo. El conjunto de atributos probados se muestrea de forma aleatoria en cada nodo del árbol de decisión.
En el siguiente árbol de decisión, se ilustra el muestreo de atributos o funciones. Aquí, un árbol de decisión se entrena en 5 atributos (f1-f5). Los nodos azules representan las funciones probadas, mientras que los blancos no se probaron. La condición se crea a partir de las funciones mejor probadas (representadas con un contorno rojo).
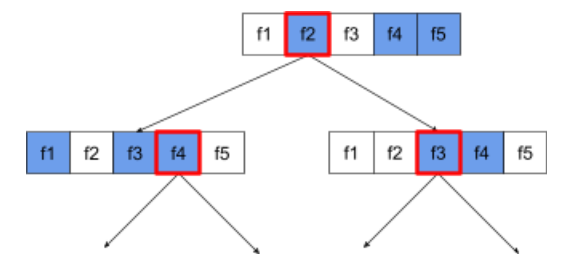
Figura 21. Muestreo de atributos.
La proporción de muestreo de atributos es un hiperparámetro de regularización importante. En la figura anterior, se usó una relación de ~⅗. Muchas implementaciones de bosques aleatorios prueban, de forma predeterminada, 1/3 de los atributos para la regresión y sqrt(cantidad de atributos) para la clasificación.
En TF-DF, los siguientes hiperparámetros controlan el muestreo de atributos:
num_candidate_attributesnum_candidate_attributes_ratio
Por ejemplo, si num_candidate_attributes_ratio=0.5, se probará la mitad de las funciones en cada nodo.
Inhabilita la regularización del árbol de decisión
Los árboles de decisión individuales en un bosque aleatorio se entrenan sin poda. (consulta Sobreajuste y poda). Esto produce árboles demasiado complejos con una calidad predictiva deficiente. En lugar de regularizar árboles individuales, los árboles se agrupan para producir predicciones generales más precisas.
Esperamos que la precisión del entrenamiento y la prueba de un bosque aleatorio difieran. La precisión del entrenamiento de un bosque aleatorio suele ser mucho mayor (a veces, igual al 100%). Sin embargo, una exactitud de entrenamiento muy alta en un bosque aleatorio es normal y no indica que el bosque aleatorio esté sobreajustado.
Las dos fuentes de aleatoriedad (bagging y muestreo de atributos) garantizan la independencia relativa entre los árboles de decisión. Esta independencia corrige el sobreajuste de los árboles de decisión individuales. En consecuencia, el conjunto no está sobreajustado. Ilustraremos este efecto no intuitivo en la siguiente unidad.
Los bosques aleatorios puros se entrenan sin profundidad máxima ni cantidad mínima de observaciones por hoja. En la práctica, es beneficioso limitar la profundidad máxima y la cantidad mínima de observaciones por hoja. De forma predeterminada, muchos bosques aleatorios usan los siguientes valores predeterminados:
- profundidad máxima de alrededor de 16
- cantidad mínima de observaciones por hoja de alrededor de 5.
Puedes ajustar estos hiperparámetros.
La claridad del ruido
¿Por qué el ruido aleatorio mejoraría la calidad de un bosque aleatorio? Para ilustrar los beneficios del ruido aleatorio, en la Figura 22 se muestran las predicciones de un árbol de decisión clásico (podado) y un bosque aleatorio entrenado en algunos ejemplos de problemas simples de dos dimensiones con un patrón de elipse.
Los patrones de elipses son muy difíciles de aprender para los algoritmos de árboles de decisión y bosques de decisión con condiciones alineadas con el eje, por lo que son un buen ejemplo. Observa que el árbol de decisión podado no puede obtener la misma calidad de predicción que el bosque aleatorio.
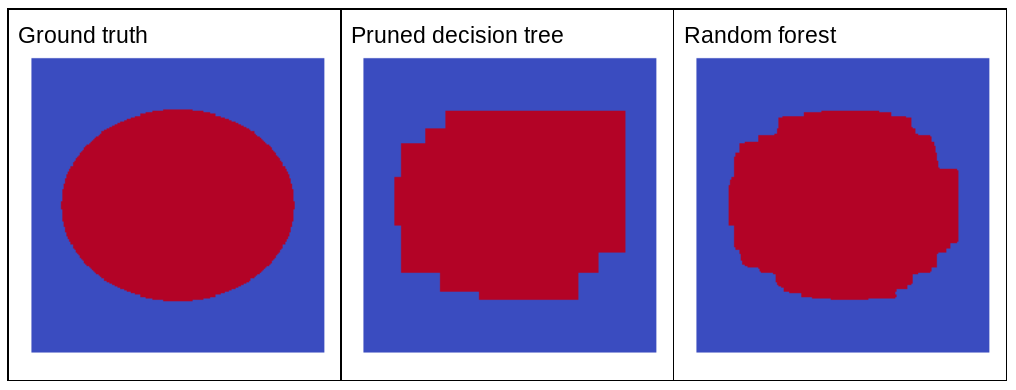
Figura 22. Verdad fundamental en comparación con las predicciones generadas por un solo árbol de decisión recortado y las predicciones generadas por un bosque aleatorio.
En el siguiente gráfico, se muestran las predicciones de los primeros tres árboles de decisión no podados del bosque aleatorio; es decir, los árboles de decisión se entrenan con una combinación de lo siguiente:
- bagging
- muestreo de atributos
- inhabilitar la reducción
Observa que las predicciones individuales de estos tres árboles de decisión son peores que las predicciones del árbol de decisión podado en la figura anterior. Sin embargo, como los errores de los árboles de decisión individuales solo están correlacionados de manera débil, los tres árboles de decisión se combinan en un conjunto para crear predicciones eficaces.
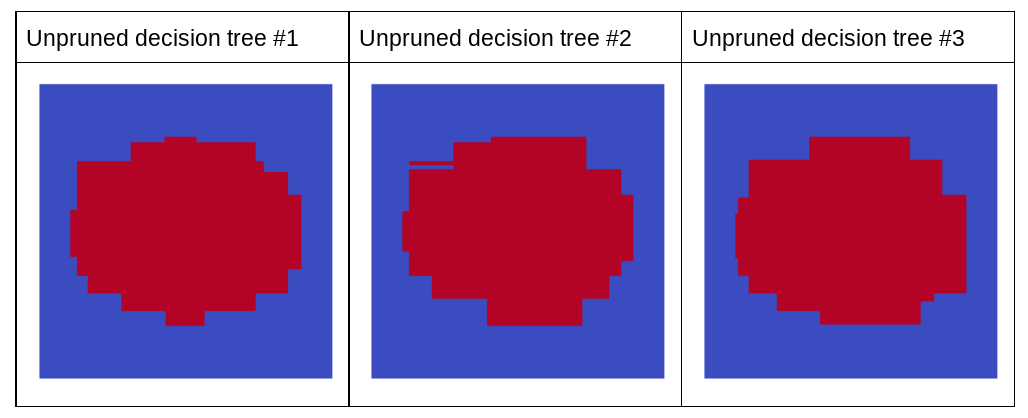
Figura 23. Tres árboles de decisión sin podar que crearán un conjunto eficaz.
Debido a que los árboles de decisión de un bosque aleatorio no se podan, el entrenamiento de un bosque aleatorio no requiere un conjunto de datos de validación. En la práctica, y en especial en conjuntos de datos pequeños, los modelos deben entrenarse con todos los datos disponibles.
Cuando se entrena un bosque aleatorio, a medida que se agregan más árboles de decisión, el error casi siempre disminuye; es decir, la calidad del modelo casi siempre mejora. Sí, agregar más árboles de decisión casi siempre reduce el error del bosque aleatorio. En otras palabras, agregar más árboles de decisión no puede hacer que el bosque aleatorio se ajuste en exceso. En algún momento, el modelo deja de mejorar. Leo Breiman dijo: “Los bosques aleatorios no se ajustan en exceso, ya que se agregan más árboles”.
Por ejemplo, en la siguiente gráfica, se muestra la evaluación de prueba de un modelo de bosque aleatorio a medida que se agregan más árboles de decisión. La precisión mejora rápidamente hasta alcanzar un punto máximo alrededor de 0.865. Sin embargo, agregar más árboles de decisión no hace que disminuya la precisión; en otras palabras,el modelo no se ajusta en exceso. Este comportamiento es (en su mayoría) siempre verdadero e independiente de los hiperparámetros.
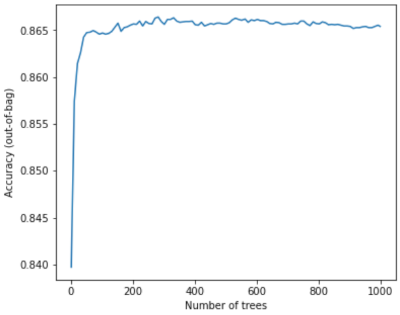
Figura 24. La precisión se mantiene constante a medida que se agregan más árboles de decisión al bosque aleatorio.