ランダム フォレスト
ランダム フォレスト(RF)は、各ディシジョン ツリーが特定のランダム ノイズでトレーニングされるディシジョン ツリーのアンサンブルです。ランダム フォレストは、ディシジョン ツリー アンサンブルで最も一般的な形式です。このユニットでは、効果的なランダム フォレストを構築する可能性を高めるために、独立したディシジョン ツリーを作成するいくつかの手法について説明します。
バギング
Bagging(bootstrap aggregating)とは、トレーニング セット内のサンプルのランダムなサブセットで各ディシジョン ツリーをトレーニングすることを意味します。つまり、ランダム フォレストの各ディシジョン ツリーは、サンプルの異なるサブセットでトレーニングされます。
バギングは特殊です。各ディシジョン ツリーは、元のトレーニング セットと同じ数のサンプルでトレーニングされます。たとえば、元のトレーニング セットに 60 個のサンプルが含まれている場合、各決定木は 60 個のサンプルでトレーニングされます。ただし、バギングでは、これらの例のサブセット(通常は 67%)でのみ各ディシジョン ツリーをトレーニングします。したがって、特定のディシジョン ツリーをトレーニングする際に、サブセット内の 40 個のサンプルの一部を再利用する必要があります。この再利用は「置換あり」のトレーニングと呼ばれます。
たとえば、表 6 は、バギングで 6 つのサンプルを 3 つのディシジョン ツリーに分散する方法を示しています。次の点に注意してください。
- 各ディシジョン ツリーは、合計 6 個のサンプルでトレーニングされます。
- 各ディシジョン ツリーは、異なるサンプルセットでトレーニングされます。
- 各ディシジョン ツリーは特定の例を再利用します。たとえば、例 4 はトレーニング ディシジョン ツリー 1 で 2 回使用されるため、ディシジョン ツリー 1 では例 4 の学習済み重みが実質的に 2 倍になります。
表 6. 3 つのディシジョン ツリーに 6 つのトレーニング サンプルをバギングします。各数値は、特定のトレーニング例(#1 ~ 6)が特定の分類ツリー(1 ~ 3)のトレーニング データセットで繰り返される回数を表します。
| トレーニング サンプル | ||||||
|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | |
| 元のデータセット | 1 | 1 | 1 | 1 | 1 | 1 |
| ディシジョン ツリー 1 | 1 | 1 | 0 | 2 | 1 | 1 |
| ディシジョン ツリー 2 | 3 | 0 | 1 | 0 | 2 | 0 |
| ディシジョン ツリー 3 | 0 | 1 | 3 | 1 | 0 | 1 |
バギングでは、ほとんどの場合、各決定木は元のトレーニング セットの全サンプル数でトレーニングされます。各ディシジョン ツリーをより多くの例またはより少ない例でトレーニングすると、ランダム フォレストの品質が低下する傾向があります。
元のランダム フォレストに関する論文には記載されていませんが、サンプルのサンプリングは「入れ替えなし」で行われる場合もあります。つまり、トレーニング サンプルをディシジョン ツリー トレーニング セットに複数回含めることはできません。たとえば、上の表では、すべての値が 0 または 1 になります。
bootstrap_training_dataset=False属性サンプリング
属性サンプリングとは、使用可能なすべての特徴に対して最適な条件を探すのではなく、各ノードで特徴のランダムなサブセットのみをテストすることを意味します。テスト対象の特徴セットは、ディシジョン ツリーの各ノードでランダムにサンプリングされます。
次の意思決定ツリーは、属性 / 特徴のサンプリングを示しています。ここでは、5 つの特徴量(f1 ~ f5)でディシジョン ツリーがトレーニングされています。青いノードはテスト対象の機能を示し、白いノードはテスト対象外です。条件は、テストが最も行われた特徴(赤い枠線で示されています)から作成されます。
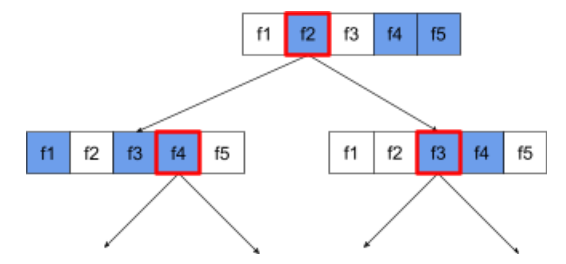
図 21. 属性サンプリング。
属性サンプリングの比率は、重要な正則化ハイパーパラメータです。上の図では、約 ⅗ の比率を使用しています。多くのランダム フォレスト実装では、デフォルトで回帰の場合は特徴量の 1/3、分類の場合は sqrt(特徴量の数)をテストします。
TF-DF では、次のハイパーパラメータによって属性サンプリングが制御されます。
num_candidate_attributesnum_candidate_attributes_ratio
たとえば、num_candidate_attributes_ratio=0.5 の場合、各ノードで特徴の半分がテストされます。
ディシジョン ツリーの正則化を無効にする
ランダム フォレストの個々のディシジョン ツリーは、プルーニングなしでトレーニングされます。(過剰適合とプルーニングをご覧ください)。これにより、予測品質が低下する過度に複雑なツリーが生成されます。個々のツリーを正規化する代わりに、ツリーをアンサンブルして、より正確な全体的な予測を生成します。
ランダム フォレストのトレーニング精度とテスト精度は異なることが想定されます。ランダム フォレストのトレーニング精度は通常ははるかに高くなります(100% に等しい場合もあります)。ただし、ランダム フォレストのトレーニング精度が非常に高いことは正常であり、ランダム フォレストが過剰適合していることを示すものではありません。
2 つのランダム性(バギングと属性サンプリング)により、決定木間の相対的な独立性が確保されます。この独立性により、個々のディシジョン ツリーの過剰適合が修正されます。その結果、アンサンブルは過剰適合しません。この直感に反する効果については、次のユニットで説明します。
純粋なランダム フォレストは、リーフあたりの最大深度や最小観測数なしでトレーニングします。実際には、リーフあたりの最大深度と最小観測数を制限することをおすすめします。デフォルトでは、多くのランダム フォレストは次のデフォルトを使用します。
- 最大深度: 約 16
- リーフあたりの最小観測数は 5 程度です。
これらのハイパーパラメータは調整できます。
ノイズの明瞭度
ランダムなノイズがランダム フォレストの品質を向上させるのはなぜですか?ランダムなノイズの利点を示すために、図 22 に、楕円形パターンの単純な 2 次元問題のいくつかの例でトレーニングされた、従来の(剪定された)ディシジョン ツリーとランダム フォレストの予測を示します。
楕円形のパターンは、軸に沿った条件でディシジョン ツリー アルゴリズムとディシジョン フォレスト アルゴリズムが学習するのが非常に難しいことで知られているため、良い例になります。剪定されたディシジョン ツリーは、ランダム フォレストと同じ予測品質を得ることはできません。
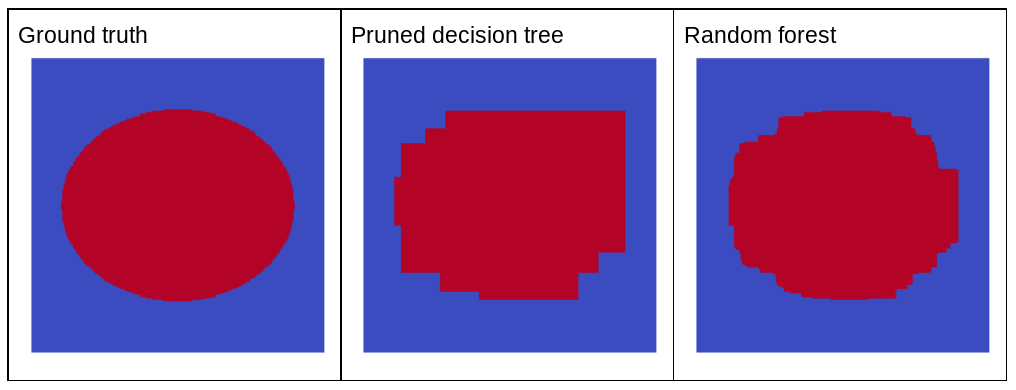
図 22. グラウンド トゥルースと、単一の剪定済み決定木によって生成された予測とランダム フォレストによって生成された予測。
次のグラフは、ランダム フォレストの最初の 3 つの剪定されていないディシジョン ツリーの予測を示しています。つまり、これらのディシジョン ツリーはすべて、次の組み合わせでトレーニングされています。
- バギング
- 属性サンプリング
- プルーニングを無効にする
これらの 3 つのディシジョン ツリーの個々の予測は、上の図の剪定されたディシジョン ツリーの予測よりも劣ることに注意してください。ただし、個々のディシジョン ツリーの誤差は弱く相関しているため、3 つのディシジョン ツリーをアンサンブルで組み合わせて、効果的な予測を作成します。
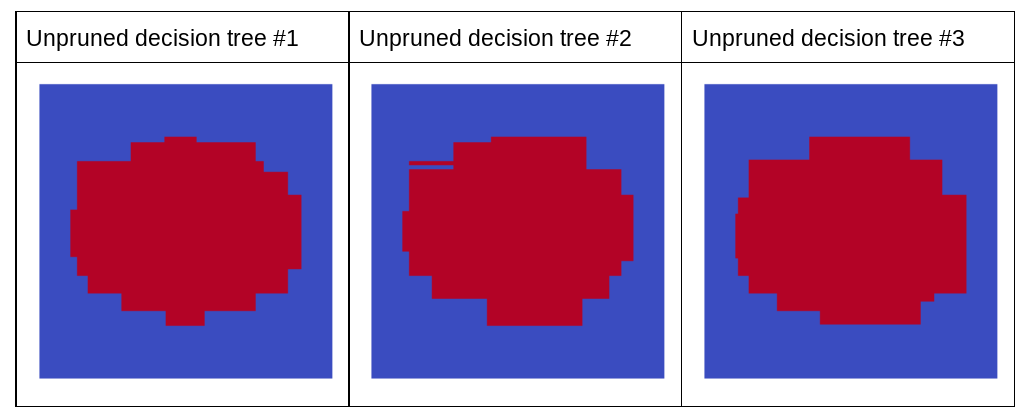
図 23. 効果的なアンサンブルを構築する、3 つの未剪定ディシジョン ツリー。
ランダム フォレストのディシジョン ツリーはプルーニングされないため、ランダム フォレストのトレーニングに検証データセットは必要ありません。実際には、特に小規模なデータセットでは、利用可能なすべてのデータでモデルをトレーニングする必要があります。
ランダム フォレストをトレーニングする際、ディシジョン ツリーを追加すると、ほとんどの場合エラーが減少します。つまり、モデルの品質が向上します。はい。ほとんどの場合、決定木を追加すると、ランダム フォレストのエラーは減少します。つまり、決定木を追加しても、ランダム フォレストのオーバーフィッティングは発生しません。ある時点で、モデルの改善は停止します。Leo Breiman は、「ランダム フォレストは、ツリーを追加しても過剰適合しない」と有名な言葉を残しています。
たとえば、次のグラフは、ディシジョン ツリーが追加されたときのランダム フォレスト モデルのテスト評価を示しています。精度は急速に向上し、0.865 付近で横ばいになります。ただし、ディシジョン ツリーを追加しても精度が低下することはありません。つまり、モデルが過剰適合することはありません。この動作は(ほとんどの場合)常に true であり、ハイパーパラメータとは関係ありません。
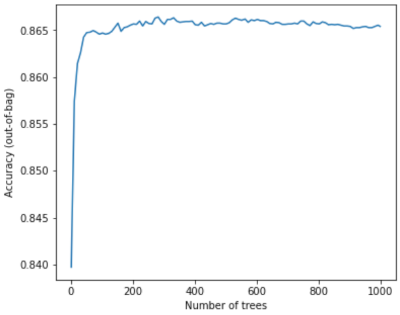
図 24. ランダム フォレストにより多くのディシジョン ツリーが追加されても、精度は一定に保たれます。