随机森林

随机森林 (RF) 是决策树的集合，其中每个决策树都使用特定的随机噪声进行训练。随机森林是最常见的决策树集成形式。本单元介绍了几种用于创建独立决策树的技术，以提高构建有效随机森林的几率。

打包

Bagging（bootstrap aggregating）是指对训练集中的随机样本子集训练每个决策树。换句话说，随机森林中的每个决策树都是基于不同的子集进行训练的。

打包很奇怪。每个决策树都使用与原始训练集中相同的示例数量进行训练。例如，如果原始训练集包含 60 个示例，则每个决策树都将使用 60 个示例进行训练。不过，抽样平均法仅针对这些示例的子集（通常为 67%）训练每个决策树。因此，在训练给定决策树时，必须重复使用该子集中的 40 个示例中的某些示例。这种重复使用称为“有替换项”训练。

例如，表 6 展示了如何将 6 个示例分布在 3 个决策树中。请注意以下几点：

• 每个决策树总共使用 6 个示例进行训练。
• 每个决策树都使用一组不同的示例进行训练。
• 每个决策树都会重复使用某些示例。例如，示例 4 在训练决策树 1 中被使用了两次；因此，示例 4 在决策树 1 中学到的权重实际上翻了一番。

表 6. 对三个决策树中的六个训练示例进行分箱。每个数字表示给定决策树 (1-3) 的训练数据集中给定训练示例 (#1-6) 的重复次数。

	训练示例
	#1	#2	#3	#4	#5	#6
原始数据集	1	1	1	1	1	1
决策树 1	1	1	0	2	1	1
决策树 2	3	0	1	0	2	0
决策树 3	0	1	3	1	0	1

在抽样法中，每个决策树几乎总是根据原始训练集中的总样本数进行训练。使用更多或更少的示例训练每个决策树往往会降低随机森林的质量。

虽然原始随机森林论文中未提及，但有时会“不替换”地对示例进行抽样；也就是说，决策树训练集中不能出现多次重复的训练示例。例如，在上表中，所有值均为 0 或 1。

YDF 代码

您可以在 YDF 中使用以下赋值启用不替换训练：bootstrap_training_dataset=False

属性抽样

属性抽样是指，在每个节点上，系统只会测试一部分随机特征，而不是在所有可用特征中寻找最佳条件。在决策树的每个节点中，系统都会随机抽取一组测试特征。

以下决策树说明了属性 / 特征抽样。 在这里，决策树是根据 5 个特征 (f1-f5) 训练的。蓝色节点表示已测试的功能，而白色节点表示未测试的功能。该条件基于经过最佳测试的特征（用红色轮廓表示）构建而成。

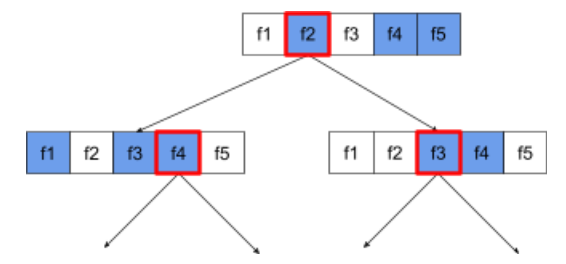
图 21. 属性抽样。

 

属性抽样比率是一项重要的正则化超参数。上图使用了 ~⅗ 的宽高比。许多随机森林实现在默认情况下会针对回归测试 1/3 的特征，针对分类测试 sqrt(特征数量) 的特征。

在 TF-DF 中，以下超参数用于控制属性抽样：

• num_candidate_attributes
• num_candidate_attributes_ratio

例如，如果为 num_candidate_attributes_ratio=0.5，则每个节点将测试一半的特征。

停用决策树正则化

随机森林中的各个决策树在训练时不会进行修剪。（请参阅过拟合和修剪）。这会生成过于复杂且预测质量较差的树。系统会对树进行组合，而不是对单个树进行正则化，从而获得更准确的整体预测结果。

注意 ：通常，大幅降低单个决策树的方差（例如，通过限制其深度）会提高单个决策树的预测质量，但会降低随机森林的预测准确性。

我们预计随机森林的训练和测试准确性会有所不同。随机森林的训练准确性通常要高得多（有时等于 100%）。不过，随机森林的训练准确率非常高是正常现象，并不表示随机森林过度拟合。

这两个随机来源（抽样和属性抽样）可确保决策树之间相对独立。这种独立性可以修正各个决策树的过拟合。因此，该模型集成不会过度拟合。我们将在下一部分中说明这种不直观的影响。

纯随机森林在训练时不设置每个叶子的最大深度或最小观察次数。在实践中，限制每个叶子的最大深度和最小观察次数是有益的。默认情况下，许多随机森林都使用以下默认设置：

• 深度上限约为 16
• 每个叶节点的最小观察次数约为 5。

您可以调整这些超参数。

YDF 代码

YDF 的 Tuner 是一种简单的超参数调节方式。如需了解详情，请参阅 YDF 的调整教程。

噪声的清晰度

为什么随机噪声会提高随机森林的质量？为了说明随机噪声的好处，图 22 显示了基于几个椭圆形模式的简单二维问题示例训练的经典（经过修剪）决策树和随机森林的预测结果。

椭圆形模式在轴心对齐条件下，决策树和决策森林算法难以学习，因此是一个很好的示例。请注意，经过修剪的决策树无法获得与随机森林相同的预测质量。

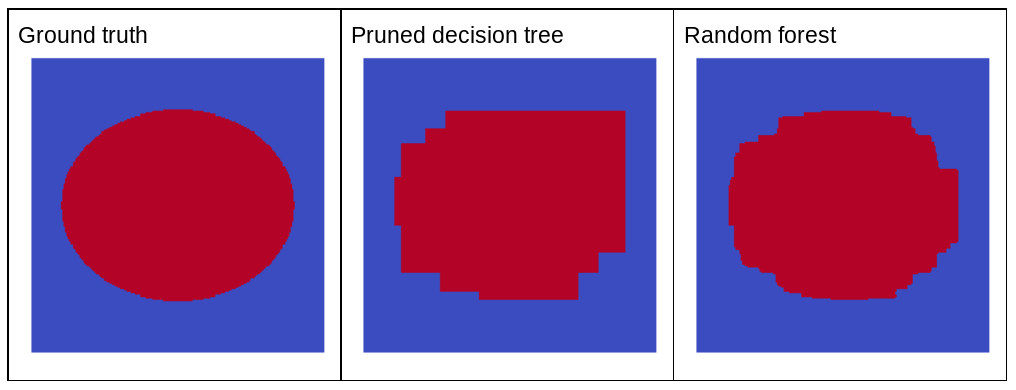
图 22. 标准答案与单个经过修剪的决策树生成的预测结果以及随机森林生成的预测结果。

下图显示了随机森林的前三个未修剪的决策树的预测结果；也就是说，这些决策树都是使用以下组合训练的：

• bagging
• 属性采样
• 停用剪枝

请注意，这三个决策树的单独预测结果不如上图中经过剪枝的决策树的预测结果。不过，由于各个决策树的误差之间只有很弱的相关性，因此这三个决策树会组合在一起，以便做出有效的预测。

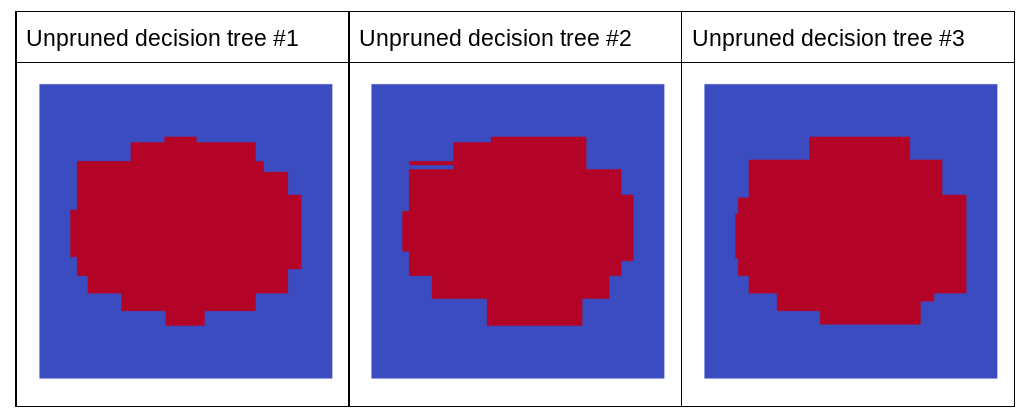
图 23. 三个未修剪的决策树，将构建一个有效的集成模型。

由于随机森林的决策树不会被修剪，因此训练随机森林不需要验证数据集。在实践中，尤其是在小数据集的情况下，应使用所有可用数据训练模型。

训练随机森林时，随着添加的决策树越来越多，误差几乎总是会减小；也就是说，模型质量几乎总是会提高。是的，增加决策树的数量几乎总会降低随机森林的误差。换句话说，添加更多决策树不会导致随机森林过拟合。在某个时候，模型会停止改进。Leo Breiman 曾说过一句名言：“随着添加更多决策树，随机森林不会过度拟合”。

例如，以下图表显示了随着添加更多决策树，随机森林模型的测试评估结果。准确性会快速提高，直到在 0.865 左右达到稳定水平。不过，添加更多决策树不会降低准确性；换句话说，模型不会过度拟合。这种行为（在大多数情况下）始终成立，并且与超参数无关。

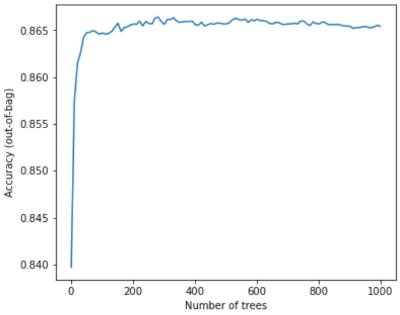
图 24. 随着向随机森林中添加更多决策树，准确性保持不变。