Florestas aleatórias

Uma floresta aleatória (RF) é um conjunto de árvores de decisão em que cada árvore de decisão é treinada com um ruído aleatório específico. Florestas aleatórias são a forma mais popular de conjunto de árvores de decisão. Nesta unidade, discutimos várias técnicas para criar árvores de decisão independentes para melhorar as chances de criar uma floresta aleatória eficaz.

Bagagem

Bagging (bootstrap aggregating) significa treinar cada árvore de decisão em um subconjunto aleatório dos exemplos no conjunto de treinamento. Em outras palavras, cada árvore de decisão da floresta aleatória é treinada em um subconjunto diferente de exemplos.

A bagagem é peculiar. Cada árvore de decisão é treinada com o mesmo número de exemplos que o conjunto de treinamento original. Por exemplo, se o conjunto de treinamento original contiver 60 exemplos, cada árvore de decisão será treinada com 60 exemplos. No entanto, o agrupamento treina apenas cada árvore de decisão em um subconjunto (geralmente 67%) desses exemplos. Portanto, alguns dos 40 exemplos no subconjunto precisam ser reutilizados ao treinar uma determinada árvore de decisão. Essa reutilização é chamada de treinamento "com substituição".

Por exemplo, a Tabela 6 mostra como o bagging pode distribuir seis exemplos em três árvores de decisão. Confira se:

• Cada árvore de decisão é treinada com um total de seis exemplos.
• Cada árvore de decisão é treinada com base em um conjunto diferente de exemplos.
• Cada árvore de decisão reutiliza determinados exemplos. Por exemplo, o exemplo no 4 é usado duas vezes na árvore de decisão de treinamento 1. Portanto, o peso aprendido do exemplo no 4 é efetivamente dobrado na árvore de decisão 1.

Tabela 6. Preparando seis exemplos de treinamento em três árvores de decisão. Cada número representa a quantidade de vezes que um determinado exemplo de treinamento (no 1 a 6) é repetido no conjunto de dados de treinamento de uma determinada árvore de decisão (1 a 3).

	exemplos de treinamento
	#1	#2	#3	#4	#5	#6
conjunto de dados original	1	1	1	1	1	1
árvore de decisão 1	1	1	0	2	1	1
árvore de decisão 2	3	0	1	0	2	0
árvore de decisão 3	0	1	3	1	0	1

No bagging, cada árvore de decisão é quase sempre treinada com base no número total de exemplos no conjunto de treinamento original. Treinar cada árvore de decisão com mais ou menos exemplos tende a degradar a qualidade da floresta aleatória.

Embora não esteja presente no documento da floresta aleatória original, a amostragem dos exemplos às vezes é feita "sem substituição", ou seja, um exemplo de treinamento não pode estar presente mais de uma vez em um conjunto de treinamento da árvore de decisão. Por exemplo, na tabela anterior, todos os valores seriam 0 ou 1.

Código YDF

É possível ativar o treinamento sem substituição com a seguinte atribuição no YDF: bootstrap_training_dataset=False

Amostragem de atributos

A amostragem de atributos significa que, em vez de procurar a melhor condição em todos os atributos disponíveis, apenas um subconjunto aleatório de atributos é testado em cada nó. O conjunto de recursos testados é amostrado aleatoriamente em cada nó da árvore de decisão.

A árvore de decisão a seguir ilustra a amostragem de atributo / recurso. Aqui, uma árvore de decisão é treinada em 5 atributos (f1-f5). Os nós azuis representam os recursos testados, enquanto os brancos não são. A condição é criada a partir dos recursos mais bem testados (representados por um contorno vermelho).

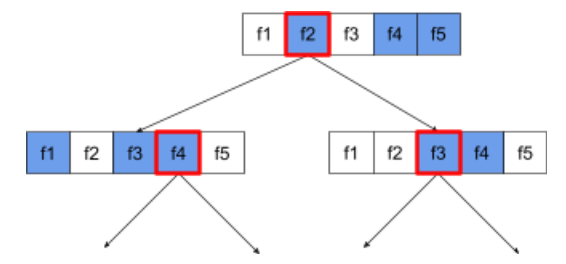
Figura 21. Amostragem de atributos.

 

A proporção da amostragem de atributos é um hiperparâmetro de regularização importante. A figura anterior usou uma proporção de ~3⁄5. Muitas implementações de floresta aleatórias testam, por padrão, 1/3 dos recursos para regressão e sqrt(número de recursos) para classificação.

No TF-DF, os hiperparâmetros a seguir controlam a amostragem de atributos:

• num_candidate_attributes
• num_candidate_attributes_ratio

Por exemplo, se for num_candidate_attributes_ratio=0.5, metade dos recursos será testado em cada nó.

Como desativar a regularização da árvore de decisão

Árvores de decisão individuais em uma floresta aleatória são treinadas sem poda. Consulte Overfitting e remoção. Isso produz árvores excessivamente complexas com baixa qualidade preditiva. Em vez de regularizar árvores individuais, elas são agrupadas, produzindo previsões gerais mais precisas.

Observação: frequentemente, reduzir agressivamente a variação de árvores de decisão individuais (por exemplo, limitando a profundidade) melhora a qualidade preditiva dessas árvores de decisão, mas diminui a precisão preditiva da floresta aleatória.

expect que a precisão do treinamento e dos testes de uma floresta aleatória seja diferente. A precisão de treinamento de uma floresta aleatória geralmente é muito maior (às vezes igual a 100%). No entanto, uma precisão de treinamento muito alta em uma floresta aleatória é normal e não indica que a floresta aleatória está sobrecarregada.

As duas fontes de aleatoriedade (bagging e amostragem de atributos) garantem a independência relativa entre as árvores de decisão. Essa independência corrige o overfitting das árvores de decisão individuais. Consequentemente, o conjunto não está overfitting. Ilustraremos esse efeito não intuitivo na próxima unidade.

Florestas aleatórias puras são treinadas sem profundidade máxima ou número mínimo de observações por folha. Na prática, é benéfico limitar a profundidade máxima e o número mínimo de observações por folha. Por padrão, muitas florestas aleatórias usam os seguintes padrões:

• profundidade máxima de ~16
• número mínimo de observações por folha de cerca de 5.

É possível ajustar esses hiperparâmetros.

Código YDF

O Tuner do YDF é uma maneira simples de ajustar hiperparâmetros. Consulte o tutorial de ajuste do YDF para mais detalhes.

A clareza do ruído

Por que um ruído aleatório melhoraria a qualidade de uma floresta aleatória? Para ilustrar os benefícios do ruído aleatório, a Figura 22 mostra as previsões de uma árvore de decisão clássica (removida) e uma floresta aleatória treinada com base em alguns exemplos de problema bidimensional simples com um padrão de elipse.

Os padrões de elipses são notoriamente difíceis para algoritmos de árvore de decisão e floresta de decisão aprenderem com condições alinhadas ao eixo, por isso são um bom exemplo. Observe que a árvore de decisão reduzida não pode ter a mesma qualidade de previsão que a floresta aleatória.

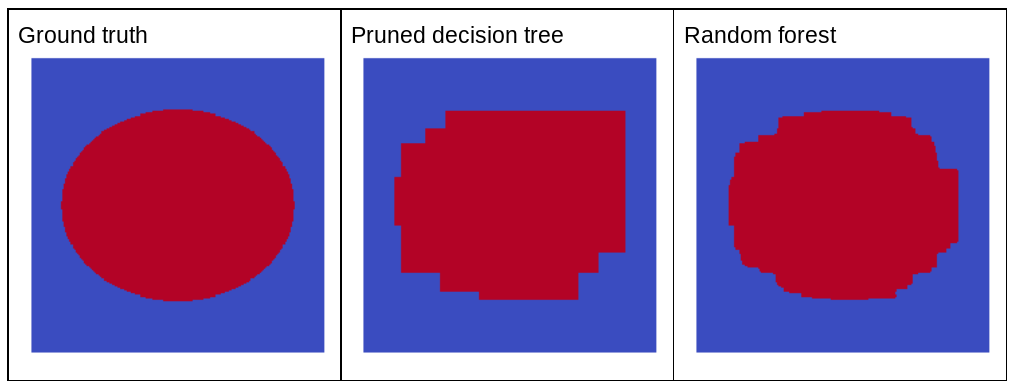
Figura 22. Informações empíricas x previsões geradas por uma única árvore de decisão removida e previsões geradas por uma floresta aleatória.

O próximo gráfico mostra as previsões das três primeiras árvores de decisão não podadas da floresta aleatória, ou seja, as árvores de decisão são todas treinadas com uma combinação de:

• enrolando
• amostragem de atributos
• desativação da remoção

Observe que as previsões individuais dessas três árvores de decisão são pioras do que as previsões da árvore de decisão reduzida na figura anterior. No entanto, como os erros das árvores de decisão individuais são apenas fracamente correlacionados, as três árvores de decisão se combinam em um conjunto para criar previsões eficazes.

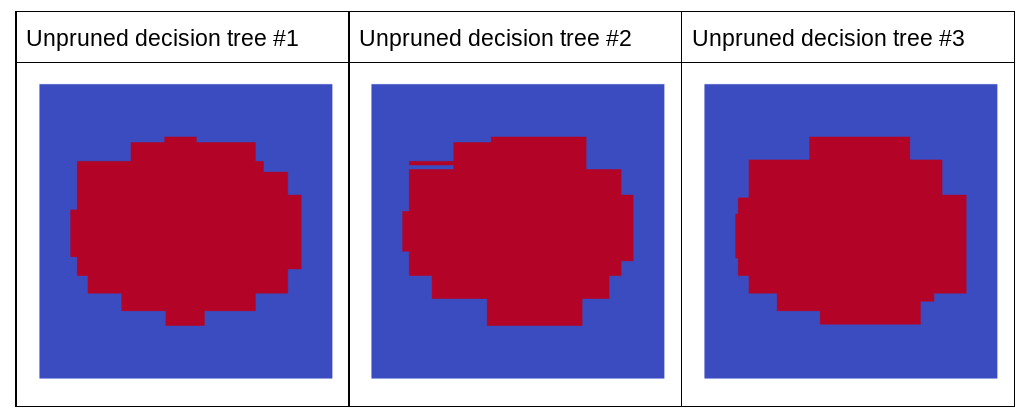
Figura 23. Três árvores de decisão não agrupadas que criarão um conjunto eficaz.

Como as árvores de decisão de uma floresta aleatória não são removidas, o treinamento de uma floresta aleatória não requer um conjunto de dados de validação. Na prática, e especialmente em pequenos conjuntos de dados, os modelos precisam ser treinados com todos os dados disponíveis.

Ao treinar uma floresta aleatória, à medida que mais árvores de decisão são adicionadas, o erro quase sempre diminui, ou seja, a qualidade do modelo quase sempre melhora. Sim, adicionar mais árvores de decisão quase sempre reduz o erro da floresta aleatória. Em outras palavras, adicionar mais árvores de decisão não pode fazer com que a floresta aleatória fique com overfitting. Em algum momento, o modelo para de melhorar. Leo Breiman disse a famosa frase: "Florestas aleatórias não se adaptam demais, porque mais árvores são adicionadas".

Por exemplo, o gráfico a seguir mostra a avaliação de teste de um modelo de floresta aleatória à medida que mais árvores de decisão são adicionadas. A precisão melhora rapidamente até ficar estável em cerca de 0,865. No entanto, adicionar mais árvores de decisão não diminui a acurácia. Em outras palavras,o modelo não causa overfitting. Esse comportamento é (na maioria) sempre verdadeiro e independente dos hiperparâmetros.

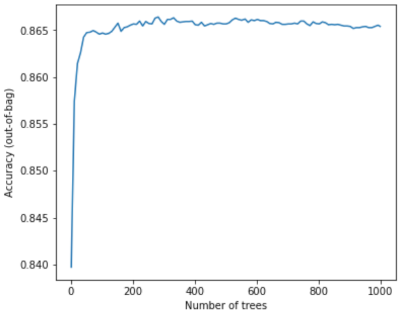
Figura 24. A precisão permanece constante à medida que mais árvores de decisão são adicionadas à floresta aleatória.