Losowe lasy
Las losowy (RF) to zbiór drzew decyzyjnych, w których każde drzewo decyzyjne jest trenowane z użyciem określonego losowego szumu. Lasy losowe to najpopularniejsza forma zbioru drzew decyzyjnych. W tej jednostce omawiamy kilka technik tworzenia niezależnych drzewek decyzyjnych, które zwiększają prawdopodobieństwo zbudowania skutecznego lasu losowego.
Opakowanie
Bagging (bootstrap aggregating) oznacza trenowanie każdego drzewa decyzyjnego na losowym podzbiorze przykładów ze zbioru treningowego. Inaczej mówiąc, każdy schemat decyzyjny w lesie losowym jest trenowany na innej podzbiorze przykładów.
Opakowanie jest dziwne. Każde drzewo decyzyjne jest trenowane na tej samej liczbie przykładów co oryginalny zbiór treningowy. Jeśli na przykład oryginalny zbiór treningowy zawiera 60 przykładów, każde drzewo decyzyjne jest trenowane na 60 przykładach. Jednak bagging trenuje każde drzewo decyzyjne tylko na podzbiorze (zazwyczaj 67%) tych przykładów. Dlatego podczas trenowania danego drzewa decyzyjnego niektóre z tych 40 przykładów w podzbiorze muszą być wykorzystywane ponownie. Takie ponowne użycie nazywamy „trenowaniem z zastąpieniem”.
Na przykład tabela 6 pokazuje, jak metoda bagging może rozprowadzić 6 przykładów na 3 drzewa decyzyjne. Pamiętaj:
- Każde drzewo decyzyjne jest trenowane na 6 przykładach.
- Każde drzewo decyzyjne jest trenowane na innym zestawie przykładów.
- Każde drzewo decyzyjne używa ponownie niektórych przykładów. Na przykład przykład 4 jest używany dwukrotnie w treningu drzewa decyzyjnego 1, dlatego w drzewie decyzyjnym 1 waga przykładu 4 jest skutecznie podwojona.
Tabela 6. Oznaczanie 6 przykładów treningowych w 3 drzewach decyzyjnych. Każda liczba wskazuje, ile razy dany przykład treningowy (1–6) powtórzył się w danym zbiorze danych treningowych (1–3) danego drzewa decyzyjnego.
| przykłady treningowe, | ||||||
|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | |
| pierwotny zbiór danych | 1 | 1 | 1 | 1 | 1 | 1 |
| drzewo decyzyjne 1 | 1 | 1 | 0 | 2 | 1 | 1 |
| decision tree 2 | 3 | 0 | 1 | 0 | 2 | 0 |
| drzewo decyzyjne 3 | 0 | 1 | 3 | 1 | 0 | 1 |
W metodzie bagging każde drzewo decyzyjne jest prawie zawsze trenowane na podstawie łącznej liczby przykładów w pierwotnym zbiorze treningowym. Trenowanie każdego drzewa decyzyjnego na większej lub mniejszej liczbie przykładów zwykle pogarsza jakość lasu losowego.
Chociaż nie jest to uwzględnione w pierwotnym artykule na temat losowego lasu, próbkowanie przykładów jest czasami wykonywane „bez zastępowania”, co oznacza, że przykład treningowy nie może występować więcej niż raz w zestawie treningowym drzewa decyzyjnego. Na przykład w poprzedniej tabeli wszystkie wartości są równe 0 lub 1.
bootstrap_training_dataset=False
Próbkowanie atrybutów
Próbkowanie atrybutów oznacza, że zamiast szukać najlepszego warunku w wszystkich dostępnych funkcjach, w każdym węźle testowana jest tylko losowa podgrupa funkcji. Zestaw testowanych cech jest losowo wybierany w każdym węźle drzewa decyzyjnego.
Poniższy schemat decyzyjny przedstawia próbkowanie atrybutów / cech. Na schemacie decyzyjnym widać drzewo wytrenowane na 5 cechach (f1–f5). Niebieskie węzły reprezentują testowane funkcje, a białe nie są testowane. Warunek jest tworzony na podstawie najlepiej przetestowanych funkcji (oznaczonych czerwoną obwódką).
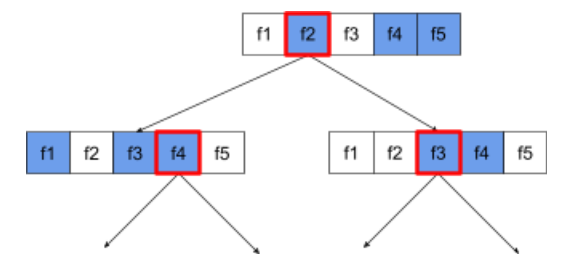
Rysunek 21. próbkowanie atrybutów.
Stosunek próbkowania atrybutów jest ważnym parametrem hiperparametrycznym regulacji. Na poprzednim rysunku użyto formatu ⅗. Wiele implementacji lasu losowego testuje domyślnie 1/3 właściwości na potrzeby regresji i sqrt(liczba właściwości) na potrzeby klasyfikacji.
W TF-DF próbkowanie atrybutów jest kontrolowane przez te parametry:
num_candidate_attributesnum_candidate_attributes_ratio
Jeśli na przykład num_candidate_attributes_ratio=0.5, na każdym węźle będzie testowana połowa funkcji.
Wyłączanie regularyzacji w schemacie decyzyjnym
Poszczególne drzewa decyzyjne w lasie losowym są trenowane bez przycinania. (zobacz Nadmiarowe dopasowanie i przycinanie). Powoduje to tworzenie zbyt złożonych drzew o niskiej jakości przewidywania. Zamiast regularyzowania poszczególnych drzew, drzewa są łączone, co daje dokładniejsze prognozy ogólne.
Spodziewamy się, że dokładność w przypadku trenowania i testowania lasu losowego będzie się różnić. Dokładność trenowania lasu losowego jest zazwyczaj znacznie wyższa (czasami równa 100%). Bardzo wysoka dokładność treningu w lasce losowym jest jednak normalna i nie wskazuje na to, że las losowy jest nadmiernie dopasowany.
Dwa źródła losowości (bagging i próbkowanie atrybutów) zapewniają względną niezależność drzewek decyzyjnych. Ta niezależność koryguje nadmierne dopasowanie poszczególnych drzew decyzyjnych. W związku z tym nie dochodzi do nadmiernego dopasowania. W następnej jednostce pokażemy, jak działa ten nieintuicyjny efekt.
Czysty las losowy trenuje bez maksymalnej głębokości ani minimalnej liczby obserwacji na element. W praktyce korzystne jest ograniczenie maksymalnej głębokości i minimalnej liczby obserwacji na pojedynczy liść. Domyślnie wiele lasów losowych korzysta z tych ustawień domyślnych:
- maksymalna głębokość to około 16
- minimalna liczba obserwacji na węzeł liścia wynosi około 5.
Możesz dostosować te hiperparametry.
przejrzystość szumów,
Dlaczego losowy szum miałby poprawić jakość losowego lasu? Aby zilustrować zalety losowego szumu, rysunek 22 przedstawia prognozy klasycznego (ostrzyżonego) drzewa decyzyjnego i lasu losowego wytrenowanych na kilku przykładach prostego dwuwymiarowego problemu z wzorcem elipsy.
W przypadku algorytmów drzewa decyzyjnego i lasu decyzyjnego wzorce elips są trudne do nauczenia się w przypadku warunków wyrównanych względem osi, dlatego stanowią dobry przykład. Pamiętaj, że przycięte drzewo decyzyjne nie może zapewnić takiej jakości prognozy jak las losowy.
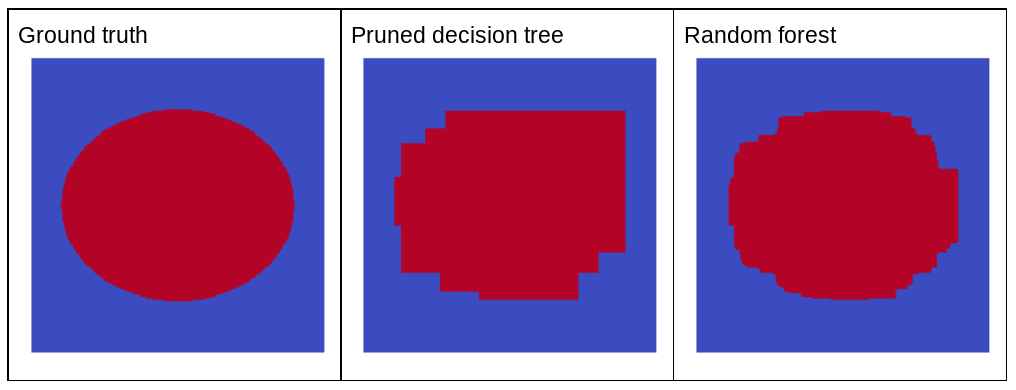
Rysunek 22. Dane rzeczywiste w porównaniu z prognozami wygenerowanymi przez pojedyncze przycięte drzewo decyzyjne i prognozami wygenerowanymi przez losowy las.
Na kolejnym wykresie widać prognozy pierwszych 3 nieoczyszczonych drzew decyzyjnych lasu losowego. Oznacza to, że wszystkie drzewa decyzyjne zostały wytrenowane na podstawie kombinacji:
- bagging
- próbkowanie atrybutów
- wyłączenie przycinania
Zwróć uwagę, że poszczególne prognozy tych 3 schematów decyzyjnych są gorsze niż prognozy schematu decyzyjnego po przycięciu na rysunku powyżej. Ponieważ jednak błędy poszczególnych drzew decyzyjnych są ze sobą tylko słabo skorelowane, 3 drzewa decyzyjne są łączone w zestaw, aby tworzyć skuteczne prognozy.
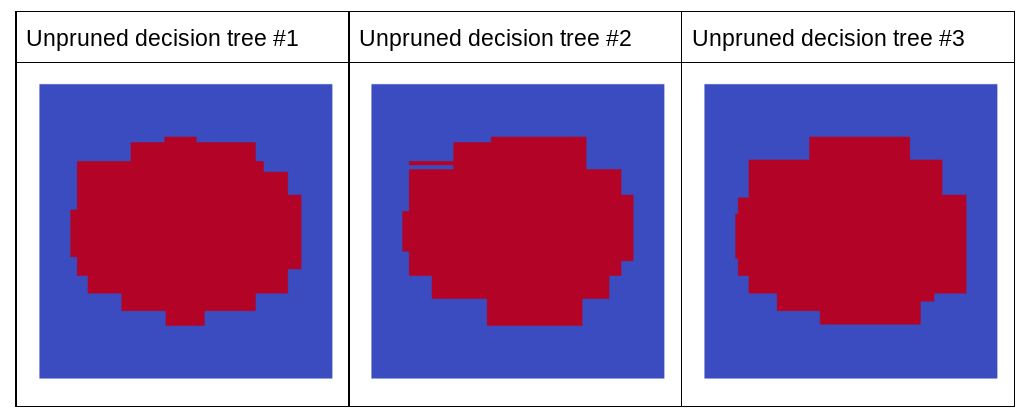
Rysunek 23. 3 nieoczyszczone drzewa decyzyjne, które utworzą skuteczny zestaw.
Ponieważ drzewa decyzyjne w lasie losowym nie są przycinane, do trenowania lasu losowego nie jest potrzebny zbiór danych do weryfikacji. W praktyce, zwłaszcza w przypadku małych zbiorów danych, modele powinny być trenowane na wszystkich dostępnych danych.
Podczas trenowania lasu losowego wraz z dodawaniem kolejnych drzewek decyzyjnych błąd prawie zawsze maleje, czyli jakość modelu prawie zawsze się poprawia. Tak, dodanie większej liczby drzewek decyzyjnych niemal zawsze zmniejsza błąd lasu losowego. Inaczej mówiąc, dodanie większej liczby drzewek decyzyjnych nie może spowodować nadmiernego dopasowania lasu losowego. W pewnym momencie model przestaje się udoskonalać. Leo Breiman słusznie zauważył, że lasy losowe nie dopasowują się nadmiernie, gdy dodawane są kolejne drzewa.
Na przykład wykres poniżej pokazuje testowanie modelu lasu losowego po dodaniu kolejnych drzewek decyzyjnych. Dokładność szybko rośnie, aż osiąga plateau na poziomie około 0,865. Dodanie większej liczby drzewek decyzyjnych nie powoduje jednak spadku dokładności. Innymi słowy, model nie jest nadmiernie dopasowywany. To zachowanie jest (z większości) zawsze prawdziwe i niezależne od hiperparametrów.
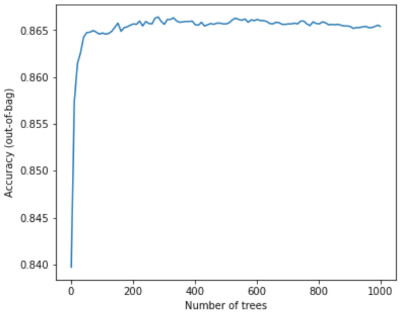
Rysunek 24. Dokładność pozostaje niezmienna, gdy do lasu losowego dodaje się kolejne drzewa decyzyjne.