本頁面列出 Decision Forests 的詞彙。如要查看所有詞彙,請按這裡。
A
屬性取樣
訓練決策樹系的策略,其中每個決策樹在學習條件時,只會考慮可能的特徵隨機子集。一般來說,每個節點會取樣不同的特徵子集。反之,如果訓練決策樹時沒有屬性取樣,系統會考慮每個節點的所有可能特徵。
軸對齊條件
在決策樹中,條件只涉及單一特徵。舉例來說,如果 area 是特徵,則下列為軸對齊條件:
area > 200
與斜線條件形成對比。
B
裝袋
這是一種訓練集合的方法,其中每個模型都會訓練隨機子集,並取樣替換訓練範例。舉例來說,隨機森林是透過袋裝法訓練的決策樹集合。
「bagging」一詞是「bootstrap aggregating」的縮寫。
詳情請參閱「決策樹林」課程中的隨機森林。
二元條件
在決策樹中,條件只有兩種可能的結果,通常是「是」或「否」。舉例來說,以下是二元條件:
temperature >= 100
與非二元條件形成對比。
詳情請參閱「決策樹林」課程中的「條件類型」。
C
狀況
在決策樹中,執行測試的任何節點。舉例來說,下列決策樹包含兩項條件:

條件也稱為「分割」或「測試」。
對比條件與 leaf。
另請參閱:
詳情請參閱「決策樹林」課程中的「條件類型」。
D
決策樹林
由多個決策樹建立的模型。決策樹林會彙整決策樹的預測結果,藉此做出預測。常見的決策樹林類型包括隨機森林和梯度提升樹狀結構。
詳情請參閱「決策樹」課程的「決策樹」一節。
決策樹狀圖
監督式學習模型,由一組以階層方式整理的條件和葉節點組成。舉例來說,以下是決策樹:
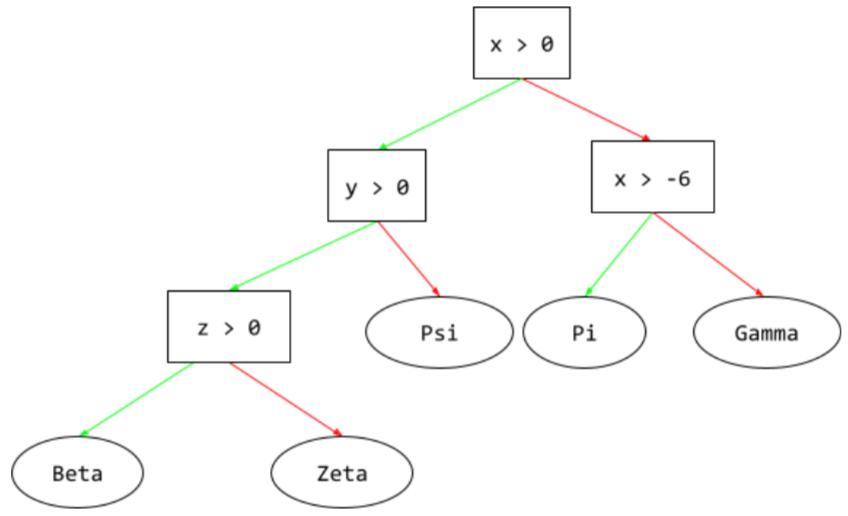
E
熵
在 資訊理論中,熵是用來描述機率分布的不可預測程度。或者,熵也可以定義為每個樣本所含的資訊量。當隨機變數的所有值都同樣可能發生時,分配的熵最高。
如果集合有兩個可能的值「0」和「1」(例如二元分類問題中的標籤),則熵的公式如下:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
其中:
- H 是熵。
- p 是「1」範例的分數。
- q 是「0」範例的分數。請注意,q = (1 - p)
- 記錄通常是記錄 2。在本例中,熵單位為位元。
舉例來說,假設:
- 100 個範例包含值「1」
- 300 個範例包含值「0」
因此,熵值為:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 每個範例 0.81 位元
如果資料集完全平衡 (例如 200 個「0」和 200 個「1」),每個樣本的熵為 1.0 位元。當集合變得越不平衡,其熵值就會越接近 0.0。
在決策樹中,熵有助於制定資訊增益,協助分割器在分類決策樹成長期間選取條件。
比較熵值與:
熵通常稱為「香農熵」。
詳情請參閱「Exact splitter for binary classification with numerical features」(使用精確分割器搭配數值特徵進行二元分類) 課程。
F
特徵重要性
變數重要性的同義詞。
G
吉尼不純度
與熵類似的指標。分割器 會使用從吉尼不純度或熵值衍生的值,組成用於分類條件的決策樹。 資訊增益是從熵值衍生而來。從吉尼不純度衍生的指標,目前沒有普遍接受的同義詞;不過,這個未命名的指標與資訊增益同樣重要。
吉尼不純度也稱為「吉尼係數」,或簡稱「吉尼」。
梯度提升 (決策) 樹狀結構 (GBT)
這是一種決策樹系,具有下列特點:
詳情請參閱決策樹林課程中的「梯度提升決策樹」。
梯度提升
訓練演算法,訓練弱模型,反覆提升強模型的品質 (減少損失)。舉例來說,線性或小型決策樹模型可能就是弱模型。強模型會成為先前訓練的所有弱模型的總和。
在最簡單的梯度提升形式中,系統會在每次疊代時訓練弱模型,以預測強模型的損失梯度。接著,系統會減去預測的梯度,藉此更新強模型的輸出內容,類似於梯度下降。
其中:
- $F_{0}$ 是起始強模型。
- $F_{i+1}$ 是下一個強大模型。
- $F_{i}$ 是目前的強大模型。
- $\xi$ 是介於 0.0 和 1.0 之間的值,稱為縮減率,類似於梯度下降中的學習率。
- $f_{i}$ 是訓練用來預測 $F_{i}$ 損失梯度的弱模型。
梯度提升的現代變體也會在運算中納入損失的二階導數 (Hessian)。
決策樹通常在梯度提升中做為弱模型。請參閱梯度提升 (決策) 樹狀結構。
I
推論路徑
在決策樹中,推論期間,特定範例會從根到其他條件,最後以葉節點終止。舉例來說,在下列決策樹中,較粗的箭頭顯示具有下列特徵值的範例推論路徑:
- x = 7
- y = 12
- z = -3
下圖中的推論路徑會經過三種情況,最後抵達葉節點 (Zeta)。

三條粗箭頭代表推論路徑。
詳情請參閱「決策樹林」課程中的決策樹。
資訊增益
在決策樹林中,節點的熵與其子項節點熵的加權 (依範例數量) 總和之間的差異。節點的熵是該節點中範例的熵。
舉例來說,請考量下列熵值:
- 父節點的熵 = 0.6
- 一個子節點的熵,有 16 個相關範例 = 0.2
- 另一個子節點的熵 (24 個相關範例) = 0.1
因此,40% 的範例位於一個子節點,60% 位於另一個子節點。因此:
- 子節點的加權熵總和 = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
因此,資訊增益為:
- 資訊增益 = 父項節點的熵 - 子項節點的加權熵總和
- 資訊增益 = 0.6 - 0.14 = 0.46
在集合條件中
在決策樹中,條件會測試一組項目中是否包含某個項目。舉例來說,以下是集合內條件:
house-style in [tudor, colonial, cape]
在推論期間,如果房屋樣式 特徵 的值為 tudor、colonial 或 cape,則此條件的評估結果為「是」。如果房屋風格特徵的值為其他內容 (例如 ranch),則這項條件的評估結果為「否」。
與測試 one-hot 編碼特徵的條件相比,集合內條件通常會產生更有效率的決策樹。
L
葉子
決策樹中的任何端點。與條件不同,葉節點不會執行測試。而是可能的預測結果。葉節點也是推論路徑的終端節點。
舉例來說,下列決策樹包含三個葉節點:
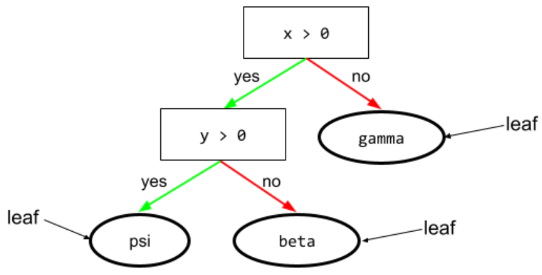
詳情請參閱「決策樹林」課程中的決策樹。
否
節點 (決策樹)
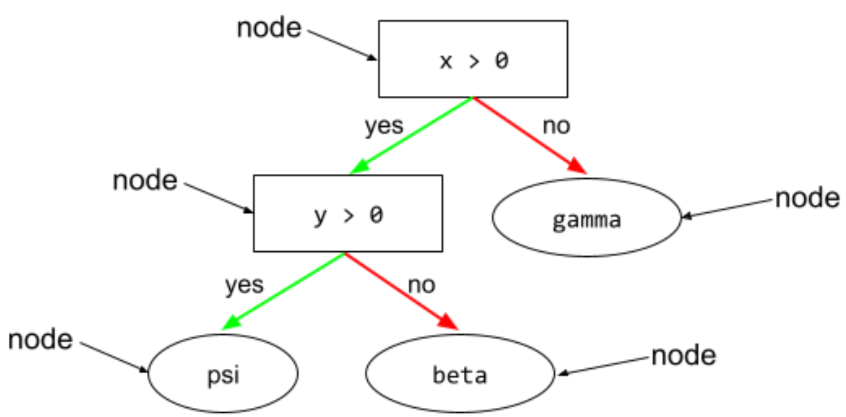
詳情請參閱決策樹林課程中的決策樹。
非二元條件
包含兩種以上可能結果的條件。舉例來說,下列非二元條件包含三種可能結果:
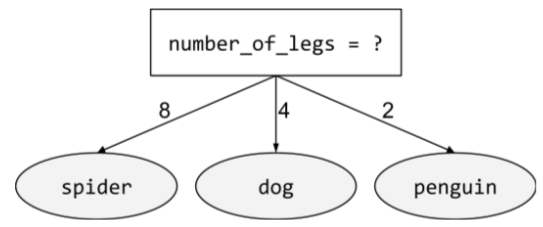
詳情請參閱「決策樹林」課程中的「條件類型」。
O
斜體條件
在決策樹中,條件涉及多個特徵。舉例來說,如果高度和寬度都是特徵,則下列為斜向條件:
height > width
與軸對齊條件形成對比。
詳情請參閱「決策樹林」課程中的「條件類型」。
袋外評估 (OOB 評估)
評估決策樹林品質的機制,方法是針對範例 (未用於該決策樹的訓練) 測試每個決策樹。舉例來說,在下圖中,系統會使用約三分之二的樣本訓練每個決策樹,然後根據其餘三分之一的樣本進行評估。
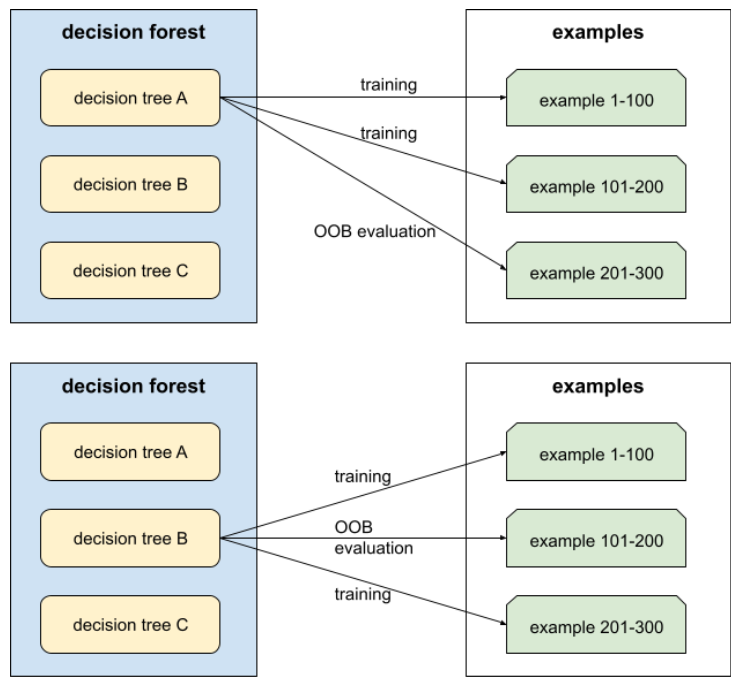
袋外評估是交叉驗證機制,可有效率地估算保守值。在交叉驗證中,每個交叉驗證回合都會訓練一個模型 (例如,在 10 折交叉驗證中,會訓練 10 個模型)。使用 OOB 評估時,系統會訓練單一模型。由於裝袋會在訓練期間保留每棵樹的部分資料,因此 OOB 評估可使用這些資料來近似交叉驗證。
詳情請參閱決策樹林課程中的袋外評估。
P
排列變數重要性
一種變數重要性,用於評估模型在特徵值經過排列後,預測錯誤率的增幅。排序變數重要性是與模型無關的指標。
R
隨機森林
隨機樹系是決策樹系的一種。
詳情請參閱決策樹課程中的「隨機森林」。
根
決策樹中的起始節點 (第一個條件)。按照慣例,圖表會將根節點放在決策樹的頂端。例如:

日
放回取樣
從一組候選項目中挑選項目的方法,可重複挑選同一項目。「可重複」是指每次選取後,所選項目會放回候選項目池。反向方法「取樣時不放回」表示候選項目只能挑選一次。
舉例來說,請考量下列水果組合:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}假設系統隨機選取 fig 做為第一個項目。
如果使用放回抽樣,系統會從下列集合中挑選第二個項目:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}沒錯,這與先前的設定相同,因此系統可能會再次選取 fig。
如果使用無替代抽樣,一旦選取樣本,就無法再次選取。舉例來說,如果系統隨機選取 fig 做為第一個樣本,就不能再次選取 fig。因此,系統會從下列 (縮減) 集合中挑選第二個樣本:
fruit = {kiwi, apple, pear, cherry, lime, mango}縮水
超參數是梯度提升中的參數,可控制過度擬合。梯度提升的收縮與梯度下降中的學習率類似。縮減率是介於 0.0 和 1.0 之間的小數值。與較大的縮減值相比,較小的縮減值可更有效地減少過度擬合。
分割
分割器
訓練決策樹時,負責在每個節點尋找最佳條件的常式 (和演算法)。
T
test
門檻 (適用於決策樹)
在軸對齊條件中,特徵要比較的值。舉例來說,在下列條件中,75 是門檻值:
grade >= 75
詳情請參閱決策樹林課程中的「Exact splitter for binary classification with numerical features」。
V
變數重要性
一組分數,代表各特徵對模型的重要性。
舉例來說,假設您要使用決策樹估算房價。假設這個決策樹使用三項特徵:尺寸、年齡和風格。如果計算出三個特徵的變數重要性為 {size=5.8, age=2.5, style=4.7},則對決策樹而言,大小比年齡或風格更重要。
變數重要性指標有很多種,可讓 ML 專家瞭解模型的不同層面。
W
群眾智慧
這個概念是指,平均大量人群 (「群眾」) 的意見或估計值,通常會產生出乎意料的良好結果。舉例來說,假設有一款遊戲是讓玩家猜測大罐子裡裝了多少顆軟糖。雖然大多數人的猜測都不準確,但實證結果顯示,所有猜測的平均值與罐子裡實際的豆子數量非常接近。
集合是群眾智慧的軟體類比。 即使個別模型做出極度不準確的預測,平均多個模型的預測結果通常會產生出乎意料的良好預測。舉例來說,雖然個別決策樹可能做出不準確的預測,但決策樹林通常能做出非常準確的預測。
