این صفحه به‌وسیله ‏Cloud Translation API‏ ترجمه شده است.

تله های تحلیلی

"همه مدل ها اشتباه هستند، اما برخی از آنها مفید هستند." - جورج باکس، 1978

اگرچه تکنیک های آماری قدرتمند، محدودیت های خود را دارند. درک این محدودیت‌ها می‌تواند به محقق کمک کند تا از گاف‌ها و ادعاهای نادرست اجتناب کند، مانند ادعای بی‌اف اسکینر مبنی بر اینکه شکسپیر بیش از پیش‌بینی تصادفی از همسان‌سازی استفاده نکرده است. (مطالعه اسکینر ضعیف بود. ¹ )

نوارهای عدم قطعیت و خطا

مهم است که عدم قطعیت را در تحلیل خود مشخص کنید. به همان اندازه مهم است که عدم قطعیت در تحلیل های دیگران را تعیین کنیم. نقاط داده ای که به نظر می رسد روندی را روی یک نمودار ترسیم می کنند، اما دارای نوارهای خطای همپوشانی هستند، ممکن است به هیچ وجه نشان دهنده هیچ الگوی نباشند. همچنین ممکن است عدم قطعیت برای نتیجه گیری مفید از یک مطالعه یا آزمون آماری خاص بسیار زیاد باشد. اگر یک مطالعه تحقیقاتی به دقت در سطح زیادی نیاز داشته باشد، یک مجموعه داده جغرافیایی با +/- 500 متر عدم قطعیت دارای عدم قطعیت زیادی است که قابل استفاده نیست.

از طرف دیگر، سطوح عدم قطعیت ممکن است در طول فرآیندهای تصمیم گیری مفید باشد. داده هایی که از یک تصفیه آب خاص با 20 درصد عدم قطعیت در نتایج پشتیبانی می کنند، ممکن است به توصیه ای برای اجرای آن تصفیه آب با نظارت مستمر برنامه برای رسیدگی به این عدم قطعیت منجر شود.

شبکه‌های عصبی بیزی می‌توانند عدم قطعیت را با پیش‌بینی توزیع مقادیر به جای مقادیر منفرد تعیین کنند.

بی ربط بودن

همانطور که در مقدمه بحث شد، همیشه حداقل یک شکاف کوچک بین داده ها و واقعیت وجود دارد. پزشک زیرک ML باید مشخص کند که آیا مجموعه داده با سؤال مطرح شده مرتبط است یا خیر.

هاف یک مطالعه اولیه افکار عمومی را توصیف می کند که نشان می دهد پاسخ سفیدپوستان آمریکایی به این سوال که چقدر برای سیاهپوستان آمریکایی آسان است زندگی خوبی داشته باشند، به طور مستقیم و معکوس با سطح همدردی آنها با سیاهپوستان آمریکایی مرتبط است. با افزایش دشمنی نژادی، پاسخ ها در مورد فرصت های اقتصادی مورد انتظار بیشتر و بیشتر خوش بینانه شد. این ممکن است به عنوان نشانه ای از پیشرفت اشتباه درک شود. با این حال، این مطالعه نمی‌توانست چیزی در مورد فرصت‌های اقتصادی واقعی موجود برای سیاه‌پوستان آمریکایی در آن زمان نشان دهد، و برای نتیجه‌گیری در مورد واقعیت بازار کار - فقط نظرات پاسخ‌دهندگان در نظرسنجی - مناسب نبود. داده های جمع آوری شده در واقع بی ربط به وضعیت بازار کار بود. ²

می توانید مدلی را بر روی داده های نظرسنجی مانند آنچه در بالا توضیح داده شد آموزش دهید، که در آن خروجی در واقع خوش بینی را به جای فرصت اندازه گیری می کند. اما از آنجایی که فرصت‌های پیش‌بینی‌شده به فرصت‌های واقعی بی‌ربط هستند، اگر ادعا می‌کنید که این مدل فرصت‌های واقعی را پیش‌بینی می‌کند، آنچه را که مدل پیش‌بینی می‌کند اشتباه نشان می‌دهید.

گیج می کند

متغیر مخدوش کننده ، مخدوش کننده یا کوفاکتور متغیری است که در حال مطالعه نیست و بر متغیرهای تحت مطالعه تأثیر می گذارد و ممکن است نتایج را مخدوش کند. به عنوان مثال، یک مدل ML را در نظر بگیرید که نرخ مرگ و میر را برای یک کشور ورودی بر اساس ویژگی های سیاست بهداشت عمومی پیش بینی می کند. فرض کنید که میانگین سنی یک ویژگی نیست. علاوه بر این، فرض کنید برخی از کشورها جمعیت مسن‌تری نسبت به سایرین دارند. با نادیده گرفتن متغیر مداخله گر سن متوسط، این مدل ممکن است نرخ مرگ و میر معیوب را پیش بینی کند.

در ایالات متحده، نژاد اغلب به شدت با طبقه اجتماعی-اقتصادی همبستگی دارد، اگرچه فقط نژاد، و نه طبقه، با داده های مرگ و میر ثبت می شود. آشفتگی های مربوط به طبقات، مانند دسترسی به مراقبت های بهداشتی، تغذیه، کار خطرناک و مسکن ایمن، ممکن است تأثیر قوی تری بر میزان مرگ و میر نسبت به نژاد داشته باشند، اما به دلیل اینکه در مجموعه داده ها گنجانده نشده اند، نادیده گرفته می شوند. ³ شناسایی و کنترل این آشفتگی‌ها برای ساخت مدل‌های مفید و نتیجه‌گیری معنادار و دقیق بسیار مهم است.

اگر مدلی بر اساس داده‌های مرگ‌ومیر موجود، که شامل نژاد است، اما نه کلاس، آموزش دیده باشد، ممکن است مرگ‌ومیر را بر اساس نژاد پیش‌بینی کند، حتی اگر کلاس پیش‌بینی‌کننده قوی‌تری برای مرگ‌ومیر باشد. این می تواند منجر به فرضیات نادرست در مورد علیت و پیش بینی های نادرست در مورد مرگ و میر بیماران شود. شاغلین ML باید بپرسند که آیا در داده های آنها آشفتگی وجود دارد و همچنین چه متغیرهای معناداری ممکن است در مجموعه داده آنها وجود نداشته باشد.

در سال 1985، مطالعه سلامت پرستاران، یک مطالعه کوهورت مشاهده‌ای از دانشکده پزشکی هاروارد و دانشکده بهداشت عمومی هاروارد، نشان داد که اعضای گروهی که درمان جایگزینی استروژن دریافت می‌کنند، در مقایسه با اعضای گروهی که هرگز استروژن مصرف نکرده‌اند، کمتر دچار حملات قلبی می‌شوند. در نتیجه، پزشکان برای چندین دهه برای بیماران یائسه و یائسه خود استروژن تجویز کردند تا اینکه یک مطالعه بالینی در سال 2002 خطرات سلامتی ناشی از استروژن درمانی طولانی مدت را شناسایی کرد. تجویز استروژن برای زنان یائسه متوقف شد، اما نه قبل از اینکه باعث مرگ زودرس ده ها هزار نفر شود.

سردرگمی های متعدد می توانست باعث ایجاد ارتباط شود. اپیدمیولوژیست ها دریافتند که زنانی که از درمان جایگزینی هورمون استفاده می کنند، در مقایسه با زنانی که این کار را نمی کنند، لاغرتر، تحصیلکرده تر، ثروتمندتر، آگاه تر از سلامتی خود و بیشتر ورزش می کنند. در مطالعات مختلف مشخص شد که تحصیلات و ثروت خطر ابتلا به بیماری قلبی را کاهش می دهد. این اثرات ممکن است ارتباط آشکار بین استروژن درمانی و حملات قلبی را مخدوش کند. ⁴

درصدهایی با اعداد منفی

در صورت وجود اعداد منفی، از استفاده از درصد خودداری کنید، زیرا ⁵ می تواند سود و زیان معنی دار را پنهان کند. برای ریاضی ساده فرض کنید صنعت رستوران داری 2 میلیون شغل دارد. اگر صنعت 1 میلیون نفر از این مشاغل را در اواخر مارس 2020 از دست بدهد، به مدت ده ماه هیچ تغییر خالصی را تجربه نکند و در اوایل فوریه 2021 900000 شغل ایجاد کند، مقایسه سال به سال در اوایل مارس 2021 تنها 5٪ را نشان می دهد. از دست دادن مشاغل رستوران با فرض عدم تغییر دیگر، مقایسه سال به سال در پایان فوریه 2022 نشان دهنده افزایش 90 درصدی مشاغل رستوران است که تصویری بسیار متفاوت از واقعیت است.

اعداد واقعی را ترجیح دهید، در صورت لزوم نرمال شده باشند. برای اطلاعات بیشتر به کار با داده های عددی مراجعه کنید.

مغالطه پسا هوک و همبستگی های غیرقابل استفاده

مغالطه پسا هوک این فرض است که، چون رویداد A با رویداد B همراه شد، رویداد A باعث رویداد B شد. به بیان ساده تر، فرض یک رابطه علت و معلولی در جایی است که یکی وجود ندارد. حتی ساده تر: همبستگی ها علیت را اثبات نمی کنند.

علاوه بر یک رابطه علت و معلولی واضح، همبستگی ها می توانند از موارد زیر نیز ناشی شوند:

شانس محض (برای مثال‌ها به همبستگی‌های جعلی تایلر ویگن، از جمله همبستگی قوی بین میزان طلاق در مین و مصرف مارگارین مراجعه کنید).
یک رابطه واقعی بین دو متغیر، اگرچه هنوز مشخص نیست که کدام متغیر مسبب است و کدام یک متأثر است.
سومین علت مجزا که بر هر دو متغیر تأثیر می گذارد، اگرچه متغیرهای همبسته با یکدیگر ارتباطی ندارند. برای مثال تورم جهانی می تواند قیمت هر دو قایق تفریحی و کرفس را افزایش دهد. ⁶

همچنین برون یابی یک همبستگی گذشته از داده های موجود خطرناک است. هاف اشاره می کند که مقداری باران باعث بهبود محصولات می شود، اما باران زیاد به آنها آسیب می رساند. رابطه بین نتایج باران و محصول غیرخطی است. ⁷ (برای اطلاعات بیشتر در مورد روابط غیرخطی به دو بخش بعدی مراجعه کنید.) جونز خاطرنشان می کند که جهان پر از رویدادهای غیرقابل پیش بینی است، مانند جنگ و قحطی، که پیش بینی های آینده داده های سری زمانی را در معرض مقادیر زیادی از عدم قطعیت قرار می دهد. ⁸

علاوه بر این، حتی یک همبستگی واقعی بر اساس علت و معلول ممکن است برای تصمیم گیری مفید نباشد. هاف، به عنوان مثال، همبستگی بین ازدواج پذیری و تحصیلات دانشگاهی در دهه 1950 را بیان می کند. زنانی که به دانشگاه می‌رفتند کمتر احتمال داشت ازدواج کنند، اما می‌توانست اینطور باشد که زنانی که به دانشگاه می‌رفتند در ابتدا تمایل کمتری به ازدواج داشتند. اگر اینطور بود، تحصیلات دانشگاهی احتمال ازدواج آنها را تغییر نداد. ⁹

اگر یک تحلیل همبستگی بین دو متغیر در یک مجموعه داده را تشخیص داد، بپرسید:

چه نوع همبستگی است: علت و معلول، رابطه جعلی، ناشناخته، یا ناشی از متغیر سوم؟
برون یابی از داده ها چقدر خطرناک است؟ هر پیش‌بینی مدل بر روی داده‌هایی که در مجموعه داده آموزشی نیستند، در واقع درون‌یابی یا برون‌یابی از داده‌ها است.
آیا می توان از همبستگی برای تصمیم گیری مفید استفاده کرد؟ به عنوان مثال، خوش‌بینی می‌تواند به شدت با افزایش دستمزدها مرتبط باشد، اما تجزیه و تحلیل احساسات مجموعه بزرگی از داده‌های متنی، مانند پست‌های رسانه‌های اجتماعی توسط کاربران در یک کشور خاص، برای پیش‌بینی افزایش دستمزدها در آن کشور مفید نخواهد بود.

هنگام آموزش یک مدل، پزشکان ML عموماً به دنبال ویژگی هایی هستند که به شدت با برچسب مرتبط هستند. اگر رابطه بین ویژگی‌ها و برچسب به خوبی درک نشده باشد، این می‌تواند منجر به مشکلاتی شود که در این بخش توضیح داده شده است، از جمله مدل‌های مبتنی بر همبستگی‌های جعلی و مدل‌هایی که فرض می‌کنند روندهای تاریخی در آینده ادامه خواهند داشت، در حالی که در واقع چنین نیستند. .

تعصب خطی

بارت دی لانگه، استفانو پانتونی و ریچارد لاریک در «تفکر خطی در دنیای غیرخطی»، سوگیری خطی را تمایل مغز انسان به انتظار و جستجوی روابط خطی توصیف می‌کنند، اگرچه بسیاری از پدیده‌ها غیرخطی هستند. برای مثال، رابطه بین نگرش و رفتار انسان، یک منحنی محدب است و نه یک خط. در مقاله ای در سال 2007 در مجله سیاست مصرف کننده به نقل از دی لانگه و همکاران، جنی ون دورن و همکاران. رابطه بین نگرانی پاسخ دهندگان نظرسنجی در مورد محیط زیست و خرید پاسخ دهندگان از محصولات ارگانیک را مدل کرد. کسانی که شدیدترین نگرانی ها را در مورد محیط زیست داشتند، محصولات ارگانیک بیشتری خریدند، اما تفاوت بسیار کمی بین سایر پاسخ دهندگان وجود داشت.

امتیاز خرید محصولات ارگانیک در مقایسه با امتیاز نگرانی‌های زیست‌محیطی، که عمدتاً یک خط صاف با یک منحنی محدب تیز به سمت بالا در سمت راست نشان می‌دهد. — نمودار خریدهای ارگانیک در مقابل امتیاز نگرانی های زیست محیطی ساده و اقتباس شده از ون دورن و همکاران. کاغذ

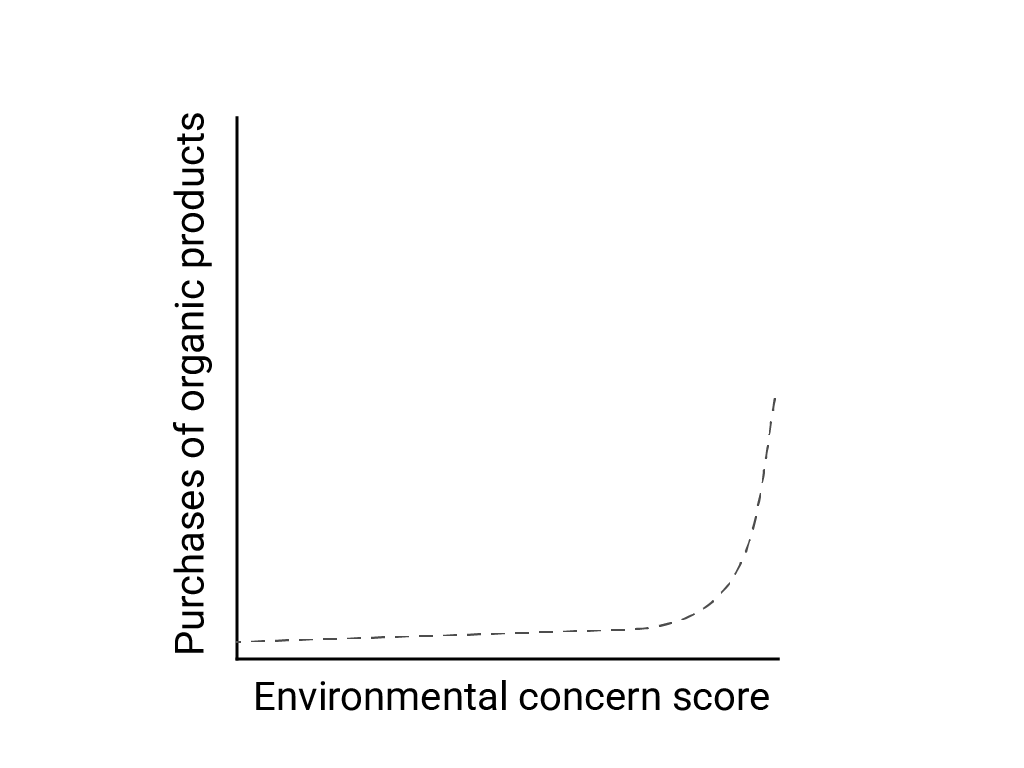
هنگام طراحی مدل ها یا مطالعات، امکان روابط غیرخطی را در نظر بگیرید. از آنجایی که آزمایش A/B ممکن است روابط غیرخطی را از دست بدهد، یک شرط سوم و میانی، C را نیز در نظر بگیرید. همچنین در نظر بگیرید که آیا رفتار اولیه که خطی به نظر می رسد خطی خواهد بود یا اینکه داده های آینده ممکن است رفتار لگاریتمی یا رفتار غیرخطی دیگری را نشان دهند.

یک برازش خطی برای داده‌های لگاریتمی که برازش خوبی را برای نیمه اول داده‌ها نشان می‌دهد و پس از آن برازش فزاینده‌ای بد را نشان می‌دهد. — مثالی از برازش خطی ضعیف با داده های لگاریتمی

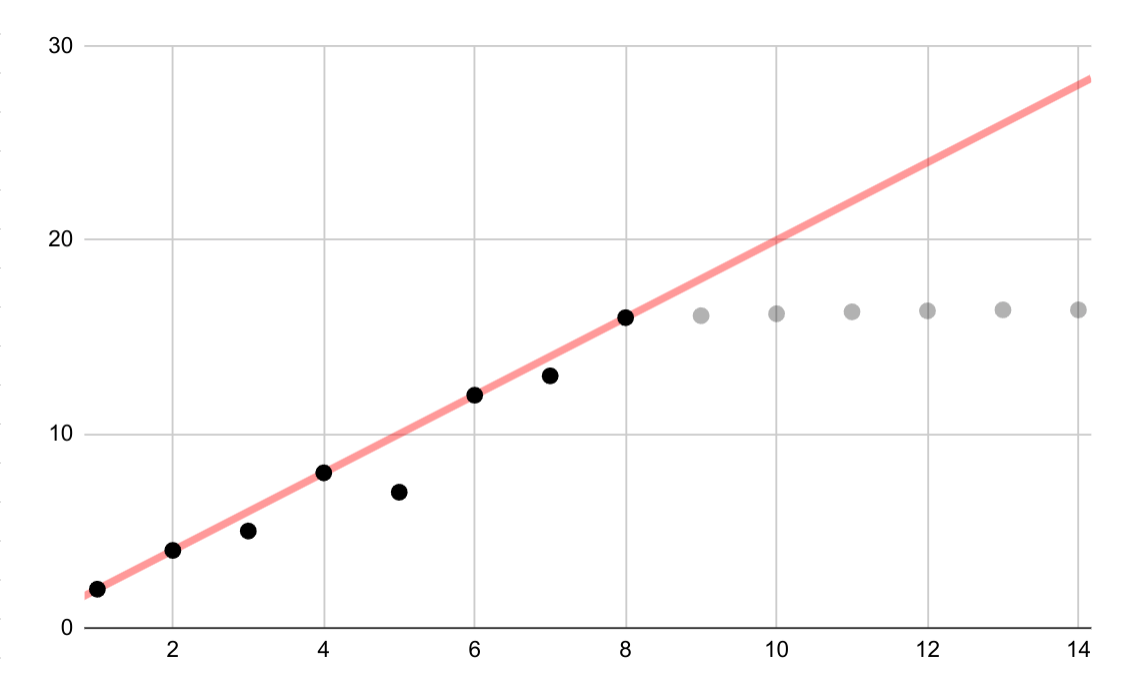
این مثال فرضی یک تناسب خطی اشتباه برای داده های لگاریتمی را نشان می دهد. اگر فقط چند نقطه داده اول در دسترس بود، فرض یک رابطه خطی مداوم بین متغیرها هم وسوسه انگیز و هم نادرست بود.

درون یابی خطی

هر گونه درونیابی بین نقاط داده را بررسی کنید، زیرا درون یابی نقاط خیالی را معرفی می کند و فواصل بین اندازه گیری های واقعی ممکن است دارای نوسانات معنی دار باشد. به عنوان مثال، تجسم زیر را از چهار نقطه داده مرتبط با درون یابی خطی در نظر بگیرید:

دامنه در طول زمان نشان دهنده چهار نقطه متصل با یک خط مستقیم است. — مثالی از درونیابی خطی

سپس این مثال از نوسانات بین نقاط داده را که با درون یابی خطی پاک می شوند در نظر بگیرید:

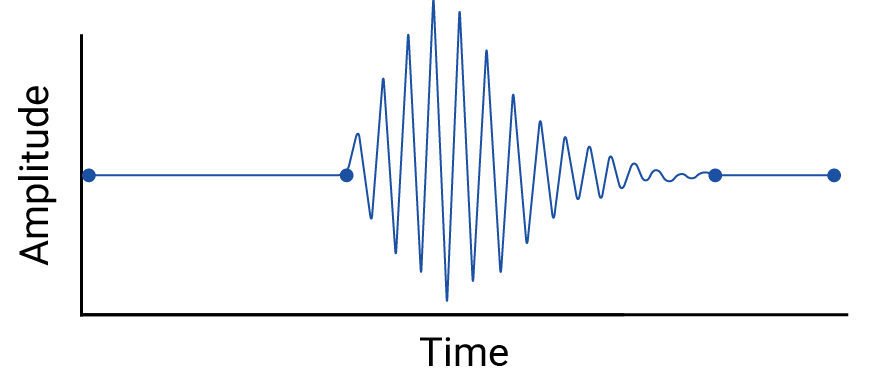
همان نقاط قبلی، اما با نوسانات عظیم بین نقاط دوم و سوم. — نمونه ای از نوسانات معنی دار (زلزله) بین نقاط داده.

این مثال به این دلیل ساخته شده است که لرزه نگارها داده های پیوسته را جمع آوری می کنند و بنابراین این زلزله از دست نمی رود. اما برای نشان دادن مفروضات ایجاد شده توسط درون یابی ها و پدیده های واقعی که متخصصان داده ممکن است از دست بدهند مفید است.

پدیده رانگ

پدیده رانگ ، که به عنوان "تکان چند جمله ای" نیز شناخته می شود، مشکلی است که در انتهای طیف از درون یابی خطی و بایاس خطی قرار دارد. هنگامی که یک درونیابی چند جمله ای را به داده ها برازش می کنیم، می توان از یک چند جمله ای با درجه بسیار بالا (درجه یا مرتبه، که بالاترین توان در معادله چند جمله ای است) استفاده کرد. این باعث ایجاد نوسانات عجیب و غریب در لبه ها می شود. به عنوان مثال، اعمال درون یابی چند جمله ای درجه 11، به این معنی که عبارت با بالاترین مرتبه در معادله چند جمله ای دارای \(x^{11}\)، به داده های تقریباً خطی، منجر به پیش بینی های بسیار بدی در ابتدا و انتهای دامنه داده ها می شود:

داده‌های تقریباً خطی با درون‌یابی چند جمله‌ای درجه 11 برازش داده می‌شوند که یک سنبله رو به بالا بین دو نقطه داده اول و یک سنبله رو به پایین تیز بین دو نقطه داده آخر را نشان می‌دهد. — مثالی از تکان دادن چند جمله ای

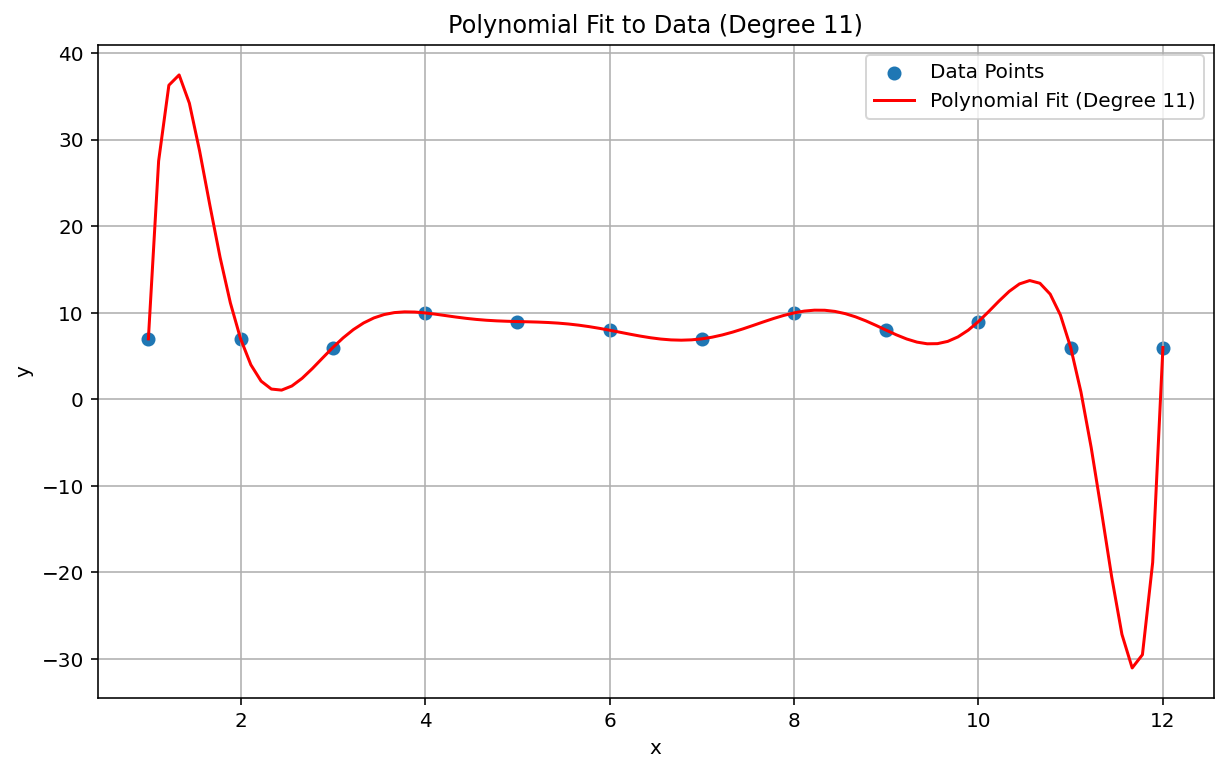
در زمینه ML، یک پدیده مشابه بیش از حد مناسب است.

شکست های آماری برای شناسایی

گاهی اوقات ممکن است یک آزمون آماری برای تشخیص یک اثر کوچک بسیار ضعیف باشد. قدرت پایین در تجزیه و تحلیل آماری به معنای شانس کم برای شناسایی صحیح رویدادهای واقعی و در نتیجه احتمال بالای منفی کاذب است. کاترین باتن و همکاران در Nature نوشت: "وقتی مطالعات در یک زمینه معین با توان 20٪ طراحی می شود، به این معنی است که اگر 100 اثر غیر پوچ واقعی در آن زمینه کشف شود، انتظار می رود این مطالعات تنها 20 مورد از آنها را کشف کنند. " افزایش حجم نمونه گاهی اوقات می تواند کمک کند، همانطور که طراحی دقیق مطالعه می تواند کمک کننده باشد.

یک وضعیت مشابه در ML مشکل طبقه بندی و انتخاب آستانه طبقه بندی است. انتخاب آستانه بالاتر منجر به مثبت کاذب کمتر و منفی کاذب بیشتر می شود، در حالی که آستانه پایین تر منجر به مثبت کاذب بیشتر و منفی کاذب کمتر می شود.

علاوه بر مسائل مربوط به قدرت آماری، از آنجایی که همبستگی برای تشخیص روابط خطی طراحی شده است، می توان همبستگی غیرخطی بین متغیرها را از دست داد. به طور مشابه، متغیرها می توانند با یکدیگر مرتبط باشند اما از نظر آماری همبستگی ندارند. متغیرها همچنین می‌توانند همبستگی منفی داشته باشند اما کاملاً نامرتبط باشند، در آنچه به عنوان پارادوکس برکسون یا مغالطه برکسون شناخته می‌شود. مثال کلاسیک مغالطه برکسون، همبستگی منفی کاذب بین هر عامل خطر و بیماری شدید هنگام نگاه کردن به جمعیت بستری در بیمارستان (در مقایسه با جمعیت عمومی) است که از فرآیند انتخاب ناشی می شود (شرایط به اندازه کافی شدید که نیاز به بستری شدن در بیمارستان دارد). .

در نظر بگیرید که آیا هر یک از این شرایط اعمال می شود یا خیر.

مدل های قدیمی و فرضیات نامعتبر

حتی مدل‌های خوب نیز می‌توانند در طول زمان تنزل پیدا کنند، زیرا ممکن است رفتار (و جهان، در این مورد) تغییر کند. مدل‌های پیش‌بینی اولیه نتفلیکس باید بازنشسته می‌شد، زیرا پایگاه مشتریان آن‌ها از کاربران جوان و آگاه به فناوری به جمعیت عمومی تغییر می‌کرد. ¹⁰

مدل‌ها همچنین می‌توانند حاوی مفروضات بی‌صدا و نادرستی باشند که ممکن است تا شکست فاجعه‌بار مدل، مانند سقوط بازار در سال 2008، پنهان بماند. مدل‌های ارزش در معرض ریسک (VaR) صنعت مالی ادعا می‌کنند که حداکثر زیان در سبد هر معامله‌گری را دقیقاً تخمین می‌زنند، می‌گویند حداکثر ضرر ۱۰۰۰۰۰ دلاری در ۹۹ درصد مواقع انتظار می‌رود. اما در شرایط غیرعادی سقوط، یک سبد با حداکثر زیان مورد انتظار 100،000 دلار ، گاهی اوقات 1،000،000 دلار یا بیشتر از دست داده است.

مدل‌های VaR مبتنی بر مفروضات معیوب هستند، از جمله موارد زیر:

تغییرات بازار گذشته پیش بینی کننده تغییرات بازار آینده است.
توزیع نرمال (دم نازک و در نتیجه قابل پیش بینی) زیربنای بازده های پیش بینی شده بود.

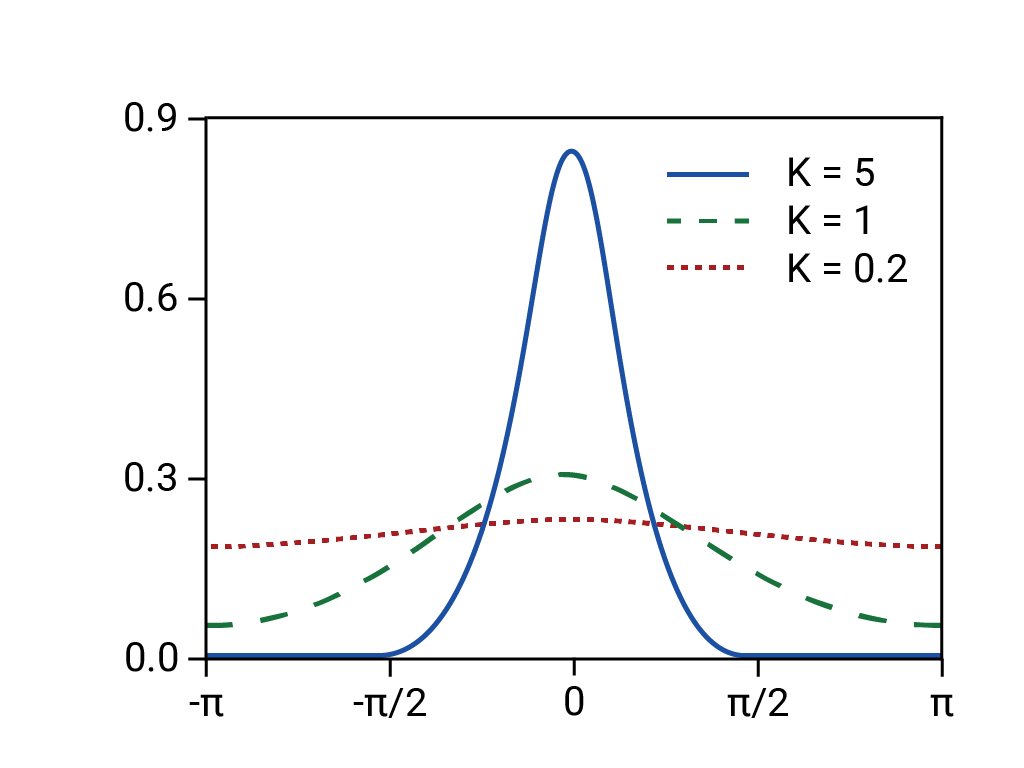
توزیع فون میزس با k=5، شبیه توزیع گاوسی، و مسطح تر k=1 و k=.2. — نمودار توزیع فون میزس، که در K بالا دم نازک و در K پایین دم چربی دارد.

در واقع، توزیع زیربنایی دم چربی، "وحشی" یا فراکتال بود، به این معنی که خطر بسیار بالاتری از رویدادهای دم بلند، شدید و ظاهراً نادر نسبت به پیش بینی توزیع عادی وجود داشت. ماهیت دم چربی توزیع واقعی به خوبی شناخته شده بود، اما به آن عمل نشد. چیزی که کمتر شناخته شده بود این بود که پدیده های مختلف تا چه حد پیچیده و محکم هستند، از جمله تجارت مبتنی بر کامپیوتر با فروش خودکار. ¹¹

مسائل تجمیع

داده هایی که تجمیع می شوند، که شامل بیشتر داده های جمعیت شناختی و اپیدمیولوژیک می شود، در معرض مجموعه خاصی از تله ها قرار می گیرند. پارادوکس سیمپسون ، یا پارادوکس ادغام ، در داده‌های انباشته رخ می‌دهد که در آن روندهای ظاهری ناپدید می‌شوند یا زمانی که داده‌ها در سطح متفاوتی تجمیع می‌شوند، به دلیل عوامل مخدوش‌کننده و روابط علّی نادرست درک شده‌اند.

مغالطه زیست‌محیطی شامل برون‌یابی اشتباه اطلاعات مربوط به یک جمعیت در یک سطح تجمع به سطح تجمعی دیگر است، جایی که ادعا ممکن است معتبر نباشد. بیماری که 40 درصد از کارگران کشاورزی را در یک استان مبتلا می کند ممکن است با شیوع یکسان در جمعیت بیشتر وجود نداشته باشد. همچنین بسیار محتمل است که مزارع یا شهرک های کشاورزی منزوی در آن استان وجود داشته باشند که شیوع مشابهی از آن بیماری را تجربه نکنند . فرض شیوع 40 درصدی در آن مکان‌های کمتر آسیب‌دیده نیز اشتباه است.

مسئله واحد منطقه ای قابل اصلاح (MAUP) یک مشکل شناخته شده در داده های مکانی است که توسط Stan Openshaw در سال 1984 در CATMOG 38 توضیح داده شده است. بسته به شکل و اندازه نواحی مورد استفاده برای تجمیع داده‌ها، متخصص داده‌های مکانی می‌تواند تقریباً هر ارتباطی را بین متغیرهای داده برقرار کند. ترسیم مناطق رای‌دهی که به نفع یک حزب یا دیگری هستند، نمونه‌ای از MAUP است.

همه این موقعیت ها شامل برون یابی نامناسب از یک سطح تجمعی به سطح دیگر است. سطوح مختلف تجزیه و تحلیل ممکن است به تجمیع‌های مختلف یا حتی مجموعه داده‌های کاملاً متفاوت نیاز داشته باشند. ¹²

توجه داشته باشید که داده‌های سرشماری، جمعیت‌شناختی و اپیدمیولوژیک معمولاً به دلایل حفظ حریم خصوصی بر اساس مناطق جمع‌آوری می‌شوند و این مناطق اغلب دلخواه هستند، یعنی بر اساس مرزهای معنی‌دار دنیای واقعی نیستند. هنگام کار با این نوع داده‌ها، پزشکان ML باید بررسی کنند که آیا عملکرد و پیش‌بینی‌های مدل بسته به اندازه و شکل مناطق انتخاب‌شده یا سطح تجمع تغییر می‌کند یا خیر، و اگر چنین است، آیا پیش‌بینی‌های مدل تحت‌تاثیر یکی از این مسائل تجمیع قرار می‌گیرد یا خیر.

مراجع

باتن، کاترین و همکاران. "شکست نیرو: چرا حجم نمونه کوچک قابلیت اطمینان علوم اعصاب را تضعیف می کند." Nature Reviews Neuroscience جلد 14 (2013)، 365-376. DOI: https://doi.org/10.1038/nrn3475

قاهره، آلبرتو نمودارها چگونه دروغ می گویند: هوشمندتر شدن در مورد اطلاعات بصری. نیویورک: WW نورتون، 2019.

Davenport, Thomas H. "A Predictive Analytics Primer." در راهنمای HBR برای مبانی تجزیه و تحلیل داده ها برای مدیران (بوستون: HBR Press، 2018) 81-86.

دی لانگه، بارت، استفانو پانتونی و ریچارد لاریک. "تفکر خطی در دنیای غیرخطی." در راهنمای HBR برای مبانی تجزیه و تحلیل داده ها برای مدیران (بوستون: HBR Press، 2018) 131-154.

النبرگ، اردن چگونه اشتباه نکنیم: قدرت تفکر ریاضی نیویورک: پنگوئن، 2014.

هاف، دارل. چگونه با آمار دروغ بگوییم نیویورک: WW نورتون، 1954.

جونز، بن. اجتناب از دام داده ها هوبوکن، نیوجرسی: وایلی، 2020.

اپن شاو، استن. «مسئله واحد مساحتی قابل تغییر»، CATMOG 38 (نرویچ، انگلستان: کتابهای جغرافیایی 1984) 37.

خطرات مدل سازی مالی: VaR و بحران اقتصادی ، کنگره 111 (2009) (شهادت های نسیم ن. طالب و ریچارد بوکستابر).

ریتر، دیوید. "چه زمانی باید بر اساس یک همبستگی عمل کرد و چه زمانی نباید". در راهنمای HBR برای مبانی تجزیه و تحلیل داده ها برای مدیران (بوستون: HBR Press، 2018) 103-109.

تولچینسکی، تئودور اچ و النا آ. واراویکووا. "فصل 3: اندازه گیری، نظارت و ارزیابی سلامت یک جمعیت" در بهداشت عمومی جدید ، ویرایش 3. San Diego: Academic Press, 2014, pp 91-147. DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.

ون دورن، جنی، پیتر سی. ورهوف، و تامو ها بیجمولت. "اهمیت روابط غیر خطی بین نگرش و رفتار در تحقیقات سیاست". مجله سیاست مصرف کننده 30 (2007) 75-90. DOI: https://doi.org/10.1007/s10603-007-9028-3

مرجع تصویر

بر اساس «توزیع فون میزس». Rainald62, 2018. منبع

النبرگ 125. ↩
هاف 77-79. هاف از دفتر تحقیقات افکار عمومی پرینستون استناد می کند، اما او ممکن است به گزارش آوریل 1944 مرکز ملی تحقیقات افکار عمومی در دانشگاه دنور فکر کرده باشد. ↩
تولچینسکی و واراویکووا. ↩
گری تابز، آیا واقعاً می دانیم چه چیزی ما را سالم می کند؟» در مجله نیویورک تایمز، 16 سپتامبر 2007. ↩
النبرگ 78. ↩
هاف 91-92. ↩
هاف 93. ↩
جونز 157-167. ↩
هاف 95. ↩
داونپورت 84. ↩
به شهادت نسیم ن. طالب و ریچارد بوکستبر در کنگره در مخاطرات مدلسازی مالی: VaR و بحران اقتصادی ، کنگره 111 (2009) 11-67 مراجعه کنید. ↩
قاهره 155، 162. ↩

"همه مدل ها اشتباه هستند، اما برخی از آنها مفید هستند." - جورج باکس، 1978

نوارهای عدم قطعیت و خطا

شبکه‌های عصبی بیزی می‌توانند عدم قطعیت را با پیش‌بینی توزیع مقادیر به جای مقادیر منفرد تعیین کنند.

بی ربط بودن

گیج می کند

اگر مدلی بر اساس داده‌های مرگ‌ومیر موجود، که شامل نژاد است، اما نه کلاس، آموزش دیده باشد، ممکن است مرگ‌ومیر را بر اساس نژاد پیش‌بینی کند، حتی اگر کلاس پیش‌بینی‌کننده قوی‌تری برای مرگ‌ومیر باشد. این می تواند منجر به فرضیات نادرست در مورد علیت و پیش بینی های نادرست در مورد مرگ و میر بیماران شود. متخصصان ML باید بپرسند که آیا در داده‌هایشان آشفتگی‌هایی وجود دارد یا خیر، و همچنین چه متغیرهای معنی‌داری ممکن است در مجموعه داده‌هایشان وجود نداشته باشد.

درصدهایی با اعداد منفی

مغالطه پسا هوک و همبستگی های غیرقابل استفاده

علاوه بر یک رابطه علت و معلولی واضح، همبستگی ها می توانند از موارد زیر نیز ناشی شوند:

شانس محض (برای مثال‌ها به همبستگی‌های جعلی تایلر ویگن، از جمله همبستگی قوی بین میزان طلاق در مین و مصرف مارگارین مراجعه کنید).
یک رابطه واقعی بین دو متغیر، اگرچه هنوز مشخص نیست که کدام متغیر مسبب است و کدام یک متأثر است.
سومین علت مجزا که بر هر دو متغیر تأثیر می گذارد، اگرچه متغیرهای همبسته با یکدیگر ارتباطی ندارند. برای مثال تورم جهانی می تواند قیمت هر دو قایق تفریحی و کرفس را افزایش دهد. ⁶

اگر یک تحلیل همبستگی بین دو متغیر در یک مجموعه داده را تشخیص داد، بپرسید:

چه نوع همبستگی است: علت و معلول، رابطه جعلی، ناشناخته، یا ناشی از متغیر سوم؟
برون یابی از داده ها چقدر خطرناک است؟ هر پیش‌بینی مدل بر روی داده‌هایی که در مجموعه داده آموزشی نیستند، در واقع درون‌یابی یا برون‌یابی از داده‌ها است.
آیا می توان از همبستگی برای تصمیم گیری مفید استفاده کرد؟ به عنوان مثال، خوش‌بینی می‌تواند به شدت با افزایش دستمزدها مرتبط باشد، اما تجزیه و تحلیل احساسات مجموعه بزرگی از داده‌های متنی، مانند پست‌های رسانه‌های اجتماعی توسط کاربران در یک کشور خاص، برای پیش‌بینی افزایش دستمزدها در آن کشور مفید نخواهد بود.

تعصب خطی

درون یابی خطی

سپس این مثال از نوسانات بین نقاط داده را که با درون یابی خطی پاک می شوند در نظر بگیرید:

همان نقاط قبل، اما با نوسانات عظیم بین نقاط دوم و سوم. — نمونه ای از نوسان معنی دار (یک زلزله) بین نقاط داده.

مثال مورد توجه قرار می گیرد زیرا لرزه نگاری داده های مداوم را جمع می کند ، بنابراین این زمین لرزه از دست نمی رود. اما برای نشان دادن فرضیات ساخته شده توسط درون یابی و پدیده های واقعی که ممکن است پزشکان داده از دست ندهند ، مفید است.

پدیده رانگ

پدیده Runge ، همچنین به عنوان "Wiggle چند جمله ای" شناخته می شود ، در انتهای مخالف طیف از درون یابی خطی و تعصب خطی مشکل است. هنگام قرار دادن درون یابی چند جمله ای به داده ها ، می توان از چند جمله ای با درجه بیش از حد بالا (درجه یا نظم ، بالاترین نماینده در معادله چند جمله ای استفاده کرد). این باعث ایجاد نوسانات عجیب و غریب در لبه ها می شود. به عنوان مثال ، استفاده از درون یابی چند جمله ای درجه 11 ، به این معنی که بالاترین مدت مرتبه در معادله چند جمله ای دارد \(x^{11}\)، به داده های تقریباً خطی ، منجر به پیش بینی های قابل ملاحظه ای در آغاز و پایان دامنه داده ها می شود:

داده های تقریباً خطی مجهز به درون یابی چند جمله ای درجه 11 ، که نشان دهنده سنبله تیز به سمت بالا بین دو نقطه داده اول و یک سنبله به سمت پایین تیز بین دو نقطه داده اخیر است — نمونه ای از wiggle چند جمله ای

در زمینه ML ، یک پدیده مشابه در حال افزایش است.

شکست های آماری در تشخیص

بعضی اوقات ممکن است یک آزمایش آماری برای تشخیص یک اثر کوچک بیش از حد تحت فشار باشد. قدرت کم در تجزیه و تحلیل آماری به معنای احتمال کم شناسایی درست وقایع واقعی است و بنابراین شانس بالایی برای منفی های کاذب است. کاترین دکمه و همکاران. در طبیعت نوشت: "هنگامی که مطالعات در یک زمینه معین با قدرت 20 ٪ طراحی شده است ، به این معنی است که اگر 100 اثر غیرقانونی واقعی وجود داشته باشد که در آن زمینه کشف شود ، انتظار می رود این مطالعات فقط 20 مورد از آنها را کشف کند. " افزایش اندازه نمونه گاهی اوقات می تواند کمک کند ، همانطور که می تواند طراحی دقیق مطالعه شود.

یک وضعیت مشابه در ML مشکل طبقه بندی و انتخاب آستانه طبقه بندی است. انتخاب آستانه بالاتر منجر به مثبت کاذب و منفی های کاذب تر می شود ، در حالی که آستانه پایین تر منجر به مثبت کاذب و منفی کاذب کمتر می شود.

علاوه بر موضوعاتی با قدرت آماری ، از آنجا که همبستگی برای تشخیص روابط خطی طراحی شده است ، همبستگی های غیرخطی بین متغیرها را می توان از دست داد. به طور مشابه ، متغیرها می توانند با یکدیگر مرتبط باشند اما از نظر آماری همبستگی ندارند. متغیرها همچنین می توانند با همبستگی منفی اما کاملاً نامربوط باشند ، در آنچه که به عنوان پارادوکس برکسون یا مغذی برکسون شناخته می شود. نمونه کلاسیک مغالطه برکسون ، همبستگی منفی حیرت انگیز بین هر عامل خطر و بیماری شدید هنگام نگاه به جمعیت بستری بیمارستان (در مقایسه با جمعیت عمومی) ، که ناشی از روند انتخاب است (یک بیماری به اندازه کافی شدید که نیاز به بستری در بیمارستان دارد) است. .

در نظر بگیرید که آیا هر یک از این شرایط اعمال می شود یا خیر.

مدل های منسوخ و فرضیات نامعتبر

حتی مدل های خوب می توانند با گذشت زمان تخریب شوند زیرا ممکن است رفتار (و جهان ، برای آن موضوع) تغییر کند. مدل های پیش بینی اولیه نتفلیکس باید بازنشسته شوند زیرا مشتری خود از کاربران جوان و با فن آوری به جمعیت عمومی تغییر می کند. ¹⁰

مدل ها همچنین می توانند حاوی فرضیات خاموش و نادرست باشند که ممکن است تا زمان خرابی فاجعه بار مدل ، مانند سقوط بازار سال 2008 ، پنهان باقی بمانند. مدلهای ارزش صنعت مالی در ریسک (VAR) ادعا می کنند که حداکثر ضرر را در سبد خریدار تخمین می زنند ، می گویند حداکثر ضرر 100000 دلار انتظار 99 ٪ از زمان را دارد. اما در شرایط غیر طبیعی این تصادف ، یک نمونه کارها با حداکثر ضرر 100000 دلار پیش بینی شده ، گاهی اوقات 1،000،000 دلار یا بیشتر از دست می داد.

مدل های VAR مبتنی بر فرضیات معیوب ، از جمله موارد زیر بودند:

تغییرات بازار گذشته پیش بینی تغییرات بازار آینده است.
توزیع نرمال (نازک و در نتیجه قابل پیش بینی) اساسی بازده پیش بینی شده بود.

توزیع فون میزس با K = 5 ، شبیه به توزیع گاوسی ، و مسطح K = 1 و K = .2. — نمودار توزیع فون میزس ، که در k بالا و دارای دم و چربی در پایین K است.

در حقیقت ، توزیع اساسی دارای چربی ، "وحشی" یا فراکتال بود ، به این معنی که خطر بسیار بیشتری از وقایع بلند ، شدید و ظاهراً نادر از آنچه که توزیع عادی پیش بینی می کرد ، وجود داشت. ماهیت چربی توزیع واقعی به خوبی شناخته شده بود ، اما بر آن عمل نمی کرد. آنچه کمتر شناخته شده بود این بود که پدیده های مختلف پیچیده و محکم همراه بودند ، از جمله تجارت مبتنی بر رایانه با فروش خودکار. ¹¹

مسائل تجمیع

داده هایی که جمع شده اند ، که شامل بیشتر داده های جمعیتی و اپیدمیولوژیک است ، در معرض مجموعه خاصی از تله ها قرار دارند. پارادوکس سیمپسون ، یا پارادوکس ادغام ، در داده های جمع شده اتفاق می افتد که در صورت جمع شدن داده ها در سطح دیگری ، روندهای ظاهری ناپدید یا معکوس می شوند ، به دلیل عوامل مخدوش کننده و سوء تفاهم روابط علّی.

مغالطه اکولوژیکی مستلزم استخراج نادرست اطلاعات در مورد جمعیت در یک سطح تجمع به سطح تجمع دیگر است ، جایی که ممکن است این ادعا معتبر نباشد. بیماری که 40 ٪ از کارگران کشاورزی در یک استان را تحت تأثیر قرار می دهد ممکن است در جمعیت بیشتر در همان شیوع وجود نداشته باشد. همچنین بسیار محتمل است که مزارع منزوی یا شهرهای کشاورزی در آن استان وجود داشته باشد که شیوع مشابه آن بیماری را تجربه نمی کنند. فرض 40 ٪ شیوع در آن مکان های کمتر تحت تأثیر قرار می گیرد.

مشکل واحد ارال قابل اصلاح (MAUP) یک مشکل مشهور در داده های جغرافیایی است که توسط استن اوپنساو در سال 1984 در Catmog 38 شرح داده شده است. بسته به شکل و اندازه مناطقی که برای جمع آوری داده ها استفاده می شود ، یک پزشک داده های جغرافیایی می تواند تقریباً هرگونه همبستگی بین متغیرهای موجود در داده ها ایجاد کند. ترسیم ولسوالی های رای گیری که به نفع یک حزب یا طرف دیگر هستند ، نمونه ای از MAUP است.

همه این شرایط شامل برون یابی نامناسب از یک سطح جمع به سطح دیگر است. سطوح مختلف تجزیه و تحلیل ممکن است نیاز به تجمع های مختلف یا حتی مجموعه داده های کاملاً متفاوت داشته باشد. ¹²

توجه داشته باشید که داده های سرشماری ، جمعیت شناختی و اپیدمیولوژیک معمولاً به دلایل حفظ حریم خصوصی توسط مناطق جمع می شوند و این مناطق اغلب دلخواه هستند ، یعنی نه بر اساس مرزهای معنی دار در دنیای واقعی. هنگام کار با این نوع داده ها ، پزشکان ML باید بررسی کنند که آیا عملکرد مدل و پیش بینی ها بسته به اندازه و شکل مناطق انتخاب شده یا سطح تجمع تغییر می کنند ، و اگر چنین است ، آیا پیش بینی های مدل تحت تأثیر یکی از این مسائل جمع قرار دارند.

مراجع

دکمه ، کاترین و همکاران. "شکست برق: چرا اندازه نمونه کوچک ، قابلیت اطمینان علوم اعصاب را تضعیف می کند." Nature Review Neuroscience Vol 14 (2013) ، 365-376. doi: https://doi.org/10.1038/nrn3475

قاهره ، آلبرتو. چگونه نمودارها دروغ می گویند: باهوش تر در مورد اطلاعات بصری. NY: WW Norton ، 2019.

Davenport ، Thomas H. "آغازگر تحلیلی پیش بینی." در راهنمای HBR مبانی تجزیه و تحلیل داده ها برای مدیران (بوستون: HBR Press ، 2018) 81-86.

د لانگ ، بارت ، استفانو پونتونی و ریچارد لاریک. "تفکر خطی در دنیای غیرخطی." در راهنمای HBR مبانی تجزیه و تحلیل داده ها برای مدیران (بوستون: HBR Press ، 2018) 131-154.

النبرگ ، اردن. چگونه اشتباه نکنیم: قدرت تفکر ریاضی. NY: پنگوئن ، 2014.

هاف ، دارل. نحوه دروغ گفتن با آمار. NY: WW Norton ، 1954.

جونز، بن. اجتناب از مشکلات داده. هابوکن ، نیویورک: ویلی ، 2020.

Openshaw ، Stan. "مشکل واحد واحد اصلاح شده" ، CATMOG 38 (نورویچ ، انگلیس: GEO Books 1984) 37.

خطرات مدل سازی مالی: VAR و Meltdown اقتصادی ، کنگره 111 (2009) (شهادت Nassim N. Taleb و Richard Bookstaber).

ریتر، دیوید. "چه موقع باید به یک همبستگی عمل کنیم ، و چه موقع نیست." در راهنمای HBR مبانی تجزیه و تحلیل داده ها برای مدیران (بوستون: HBR Press ، 2018) 103-109.

Tulchinsky ، تئودور H. و النا A. Varavikova. "فصل 3: اندازه گیری ، نظارت و ارزیابی سلامت یک جمعیت" در بهداشت عمومی جدید ، چاپ سوم. سن دیگو: انتشارات دانشگاهی ، 2014 ، صص 91-147. doi: https://doi.org/10.1016/b978-0-12-415766-8.00003-3.

ون دوورن ، جنی ، پیتر سی. ورهف و تامو هه بیجولت. "اهمیت روابط غیرخطی بین نگرش و رفتار در تحقیقات سیاست." مجله سیاست مصرف کننده 30 (2007) 75-90. doi: https://doi.org/10.1007/S10603-007-9028-3

مرجع تصویر

بر اساس "توزیع فون میزس". Rainald62 ، 2018. منبع

النبرگ 125. ↩
هاف 77-79. هاف از دفتر تحقیقات افکار عمومی پرینستون استناد می کند ، اما او ممکن است به فکر گزارش آوریل 1944 توسط مرکز تحقیقات افکار ملی در دانشگاه دنور باشد. ↩
Tulchinsky و Varavikova. ↩
گری Taubes ، آیا ما واقعاً می دانیم چه چیزی ما را سالم می کند؟ " در مجله نیویورک تایمز ، 16 سپتامبر 2007 .
النبرگ 78 .
هاف 91-92. ↩
هاف 93 .
جونز 157-167. ↩
هاف 95 .
Davenport 84 .
شهادت کنگره Nassim N. Taleb و Richard Bookstaber را در خطرات مدل سازی مالی مشاهده کنید: VAR و Meltdown اقتصادی ، کنگره 111 (2009) 11-67. ↩
قاهره 155 ، 162 .