„Wszystkie modele są złe, ale niektóre mogą być przydatne”. – George Box, 1978 r.
Chociaż są bardzo skuteczne, mają też swoje ograniczenia. Zrozumienie tych ograniczeń może pomóc badaczom uniknąć gaf i nieścisłych twierdzeń, takich jak twierdzenie BF Skinnera, że Szekspir nie używał aliteracji częściej niż przewiduje przypadkowość. (badanie Skinnera miało niewystarczającą moc1).
Niepewność i paski błędów
W analizie należy uwzględnić niepewność. Równie ważne jest określenie niepewności w analizach innych osób. Punkty danych, które na wykresie mają zaznaczony trend, ale mają nakładające się paski błędów, mogą wcale nie wskazywać żadnego wzoru. Niepewność może też być zbyt wysoka, aby wyciągnąć przydatne wnioski z określonego badania lub testu statystycznego. Jeśli badanie wymaga dokładności na poziomie partii, zbiór danych geoprzestrzennych z niepewnością +/- 500 m jest zbyt niepewny, aby można go było użyć.
Poziomy niepewności mogą być przydatne podczas podejmowania decyzji. Dane potwierdzające skuteczność określonej metody uzdatniania wody z 20% niepewnością wyników mogą skutkować rekomendacją wdrożenia tej metody z dalszym monitorowaniem programu w celu zmniejszenia tej niepewności.
Sieci neuronowe Bayesa mogą ilościowo określać niepewność, przewidując rozkłady wartości zamiast pojedynczych wartości.
Nie na temat
Jak już wspomnieliśmy we wstępie, zawsze istnieje pewna rozbieżność między danymi a rzeczywistością. Doświadczony specjalista od uczenia maszynowego powinien ustalić, czy zbiór danych jest odpowiedni do zadanego pytania.
Huff opisuje wczesne badanie opinii publicznej, które wykazało, że odpowiedzi białych Amerykanów na pytanie o to, jak łatwo jest czarnym Amerykanom zapewnić sobie dobre życie, były wprost i odwrotnie proporcjonalne do ich poziomu sympatii wobec czarnych Amerykanów. W miarę wzrostu niechęci do rasy czarnej odpowiedzi na pytania o spodziewane możliwości ekonomiczne stawały się coraz bardziej optymistyczne. Mogło to zostać zinterpretowane jako znak postępu. Badanie nie mogło jednak dać żadnych informacji o faktycznych możliwościach ekonomicznych, jakie w tym czasie mieli czarnoskórzy Amerykanie, i nie było odpowiednie do wyciągania wniosków o rzeczywistości na rynku pracy – zawierało tylko opinie respondentów. Zebrane dane nie miały nic wspólnego ze stanem rynku pracy.2
Model można wytrenować na podstawie danych z ankiety, takich jak opisane powyżej, w których przypadku dane wyjściowe służą do pomiaru optymizmu, a nie potencjału. Ponieważ jednak przewidywane możliwości nie mają nic wspólnego z rzeczywistymi możliwościami, jeśli zaczniesz twierdzić, że model przewiduje rzeczywiste możliwości, będzie to wprowadzać użytkowników w błąd co do tego, co tak naprawdę przewiduje model.
Zaciemnianie
Zmienna zakłócająca, zakłócenie lub współczynnik to zmienna, której nie badamy, a która wpływa na zmienne, które badamy, i może zniekształcać wyniki. Weźmy na przykład model ML, który przewiduje wskaźniki umieralności w danym kraju na podstawie cech polityki zdrowia publicznego. Załóżmy, że mediana wieku nie jest cechą. Załóżmy też, że w niektórych krajach mieszkają starsi ludzie. Pominięcie zmiennej zakłócającej, jaką jest mediana wieku, może spowodować, że model prognozuje błędne wskaźniki umieralności.
W Stanach Zjednoczonych rasa jest często silnie powiązana z klasą społeczno-ekonomiczną, ale w danych o śmiertelności uwzględnia się tylko rasę, a nie klasę. Czynniki zakłócające związane z klasą społeczną, takie jak dostęp do opieki zdrowotnej, odżywiania, pracy w niebezpiecznych warunkach i mieszkania w bezpiecznym miejscu, mogą mieć większy wpływ na wskaźniki umieralności niż rasa, ale mogą być pomijane, ponieważ nie są uwzględniane w danych.3 Identyfikowanie i kontrolowanie tych czynników zakłócających ma kluczowe znaczenie dla tworzenia przydatnych modeli i wyciągania wiarygodnych i dokładnych wniosków.
Jeśli model jest trenowany na podstawie dotychczasowych danych o śmiertelności, które obejmują rasę, ale nie klasę, może przewidywać śmiertelność na podstawie rasy, nawet jeśli klasa jest lepszym czynnikiem prognostycznym śmiertelności. Może to prowadzić do nieprawidłowych założeń dotyczących przyczynowości i nieprawidłowych prognoz dotyczących śmiertelności pacjentów. Specjaliści zajmujący się uczeniem maszynowym powinni zastanowić się, czy w ich danych występują czynniki zakłócające, a także jakie istotne zmienne mogą być w ich zbiorze danych.
W 1985 r. w ramach badania Nurses' Health Study, czyli obserwacyjnego badania kohortowego przeprowadzonego przez Harvard Medical School i Harvard School of Public Health, stwierdzono, że uczestnicy kohorty przyjmujący estrogen w ramach terapii zastępczej rzadziej chorowali na zawał serca w porównaniu z uczestnikami kohorty, którzy nigdy nie przyjmowali estrogenu. W rezultacie przez dziesiątki lat lekarze przepisują estrogen pacjentkom w menopauzie i po menopauzie, aż w 2002 r. w ramach badania klinicznego zidentyfikowano zagrożenia dla zdrowia związane z długotrwałą terapią estrogenową. Praktyka przepisywania estrogenu kobietom po menopauzie została wstrzymana, ale nie wcześniej niż po tym, jak spowodowała dziesiątki tysięcy przedwczesnych zgonów.
Powiązanie mogło być spowodowane wieloma czynnikami zakłócającymi. Epidemiologowie odkryli, że kobiety, które stosują hormonalną terapię zastępczą, są zazwyczaj szczuplejsze, lepiej wykształcone, zamożniejsze, bardziej świadome swojego zdrowia i bardziej skłonne do ćwiczeń niż kobiety, które nie stosują takiej terapii. W różnych badaniach wykazano, że wykształcenie i bogactwo zmniejszają ryzyko chorób serca. Te efekty mogłyby zafałszować pozorną korelację między terapią estrogenową a zawałami serca.4
Odsetki z ujemnymi wartościami
Unikaj używania procentów, gdy występują wartości ujemne5, ponieważ mogą one ukrywać różne istotne zyski i straty. Załóżmy, że w branży gastronomicznej jest 2 miliony miejsc pracy. Jeśli pod koniec marca 2020 r. branża straci 1 milion tych miejsc pracy, nie odnotuje żadnych zmian w ciągu 10 miesięcy, a na początku lutego 2021 r. odzyska 900 tys. miejsc pracy, to na początku marca 2021 r. porównanie z poprzednim rokiem wskazywałoby na utratę zaledwie 5% miejsc pracy w restauracjach. Zakładając, że nie nastąpiły żadne inne zmiany, porównanie z roku poprzedniego na koniec kwietnia 2021 r. sugerowałoby wzrost liczby miejsc pracy w restauracji o 90%, co jest bardzo dalekie od rzeczywistości.
Preferuj rzeczywiste liczby, odpowiednio skalibrowane. Więcej informacji znajdziesz w artykule Praca z danymi liczbowymi.
Błąd doboru próby i nieprzydatne korelacje
Błąd post hoc to założenie, że skoro zdarzenie A poprzedzało zdarzenie B, to zdarzenie A spowodowało zdarzenie B. Mówiąc prościej, zakłada ona związek przyczynowo-skutkowy, którego w istocie nie ma. Jeszcze prościej: korelacje nie dowodzą przyczynowości.
Oprócz wyraźnego związku przyczynowo-skutkowego korelacje mogą też wynikać z:
- Czysty przypadek (patrz nieistotne korelacje Tylera Vigena, w tym silna korelacja między współczynnikiem rozwodów w Maine a konsumpcją margaryny).
- Rzeczywisty związek między 2 zmiennymi, choć nie wiadomo, która z nich jest zmienną wywołującą, a która zmienną zależną.
- Trzecia, osobna przyczyna, która wpływa na obie zmienne, mimo że zmienne skorelowane nie są ze sobą powiązane. Na przykład globalna inflacja może podnieść ceny jachtów i selera.6
Wyciąganie wniosków na podstawie korelacji z danych, które już masz, jest też ryzykowne. Huff zwraca uwagę, że deszcz w pewnym stopniu poprawia plony, ale zbyt obfite opady mogą je zniszczyć; związek między opadami a plonami jest nieliniowy.7 (W następnych dwóch sekcjach znajdziesz więcej informacji o związkach nieliniowych). Jones zauważa, że świat jest pełen nieprzewidywalnych wydarzeń, takich jak wojny i klęski głodu, które powodują ogromną niepewność przyszłych prognoz danych z seryjnych danych.8
Co więcej, nawet prawdziwa korelacja oparta na związku przyczynowo-skutkowym może nie być przydatna do podejmowania decyzji. Huff podaje jako przykład korelację między możliwością zawarcia małżeństwa a ukończeniem studiów wyższych w latach 50. XX w. Kobiety, które skończyły studia, rzadziej wychodziły za mąż, ale mogło się tak stać, ponieważ od początku były mniej skłonne do zamążpienia. W takim przypadku wykształcenie wyższe nie wpływa na prawdopodobieństwo zawarcia małżeństwa.9
Jeśli analiza wykryje korelację między 2 zmiennymi w zbiorze danych, zadaj te pytania:
- Jakiego rodzaju jest to korelacja: przyczynowo-skutkowa, pozorna, nieznana, spowodowana przez trzecią zmienną?
- Jak ryzykowne jest ekstrapolowanie danych? Każda prognoza modelu na podstawie danych, które nie znajdują się w zbiorze danych treningowych, jest w istocie interpolacją lub ekstrapolacją danych.
- Czy korelację można wykorzystać do podejmowania przydatnych decyzji? Na przykład optymizm może być silnie skorelowany ze wzrostem płac, ale analiza nastrojów w przypadku dużego zbioru danych tekstowych, np. postów użytkowników na portalach społecznościowych w danym kraju, nie będzie przydatna do przewidywania wzrostu płac w tym kraju.
Podczas trenowania modelu specjaliści od uczenia maszynowego zwykle szukają cech, które są silnie skorelowane z etykietą. Jeśli relacja między cechami a oznaczeniem nie jest dobrze zrozumiana, może to prowadzić do problemów opisanych w tej sekcji, w tym do modeli opartych na pozornych korelacjiach i modelach, które zakładają, że historyczne trendy będą kontynuowane w przyszłości, podczas gdy tak naprawdę tak się nie dzieje.
Błąd liniowy
W artykule „Linear Thinking in a Non-Linear World” (Linearne myślenie w nieliniowym świecie) Bart de Langhe, Stefano Puntoni i Richard Larrick opisują uprzedzenie linearne jako tendencję ludzkiego mózgu do oczekywania i wyszukiwania zależności liniowych, mimo że wiele zjawisk jest nieliniowych. Związek między nastawieniem ludzi a ich zachowaniem jest na przykład wypukłą krzywą, a nie linią. W artykule z 2007 r. opublikowanym w Journal of Consumer Policy, cytowanym przez de Langhe i współautorów, Jenny van Doorn i współautorzy przeanalizowali związek między troską respondentów ankiety o środowisko a kupowaniem przez nich produktów ekologicznych. Osoby najbardziej zaniepokojone stanem środowiska kupowały więcej produktów ekologicznych, ale między pozostałymi respondentami różnice były niewielkie.
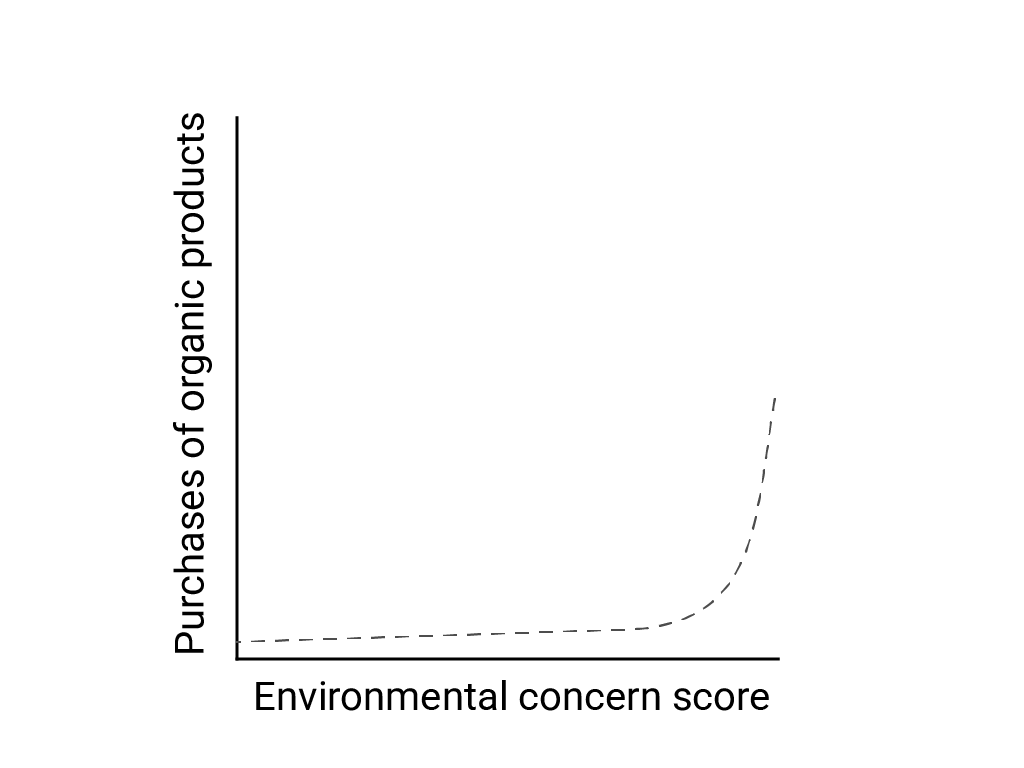
Podczas projektowania modeli lub badań należy wziąć pod uwagę możliwość występowania zależności nieliniowych. Ponieważ testy A/B mogą nie wykrywać zależności nieliniowych, rozważ przetestowanie trzeciej, pośredniej zmiennej C. Zastanów się też, czy początkowe zachowanie, które wydaje się być liniowe, pozostanie liniowe, czy też przyszłe dane mogą wykazywać charakter logaritmiczny lub inny nieliniowy.
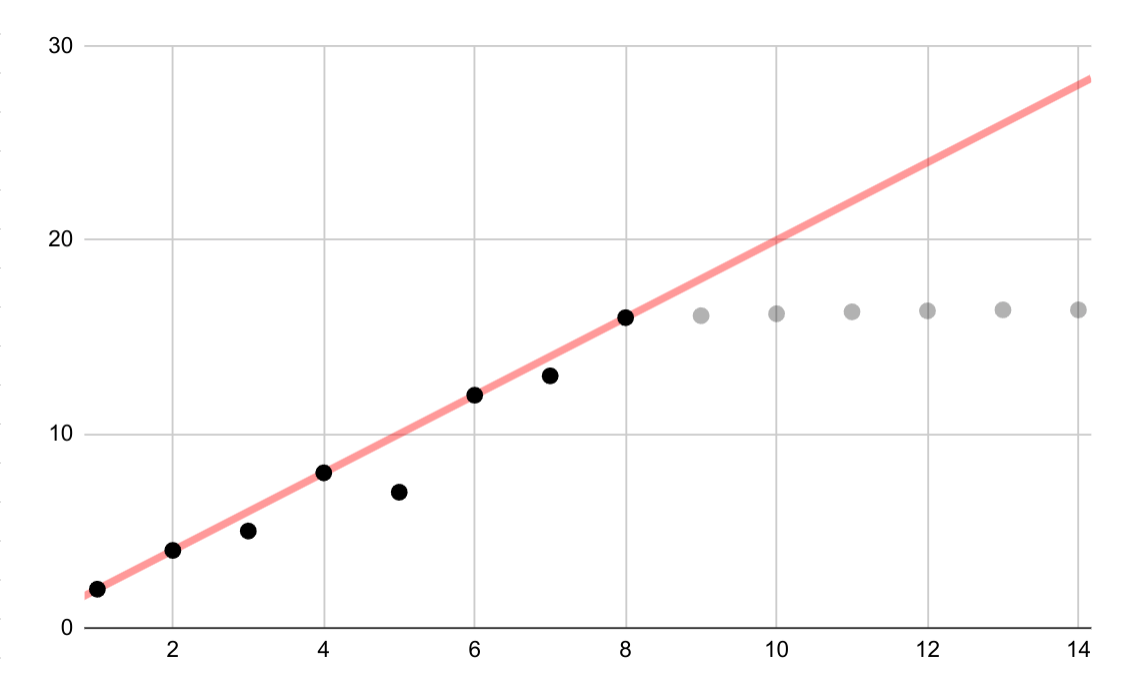
Ten przykładowy przypadek pokazuje błędny dopasowanie liniowe do danych logarytmicznych. Jeśli dostępne byłyby tylko pierwsze punkty danych, założenie stałej zależności liniowej między zmiennymi byłoby kuszące, ale nieprawidłowe.
Interpolacja liniowa
Sprawdź interpolację między punktami danych, ponieważ interpolacja wprowadza fikcyjne punkty, a przedziały między rzeczywistymi pomiarami mogą zawierać istotne wahania. Weź pod uwagę tę wizualizację 4 punktów danych połączonych interpolacją liniową:

Następnie rozważ ten przykład wahań między punktami danych, które są usuwane przez interpolację liniową:
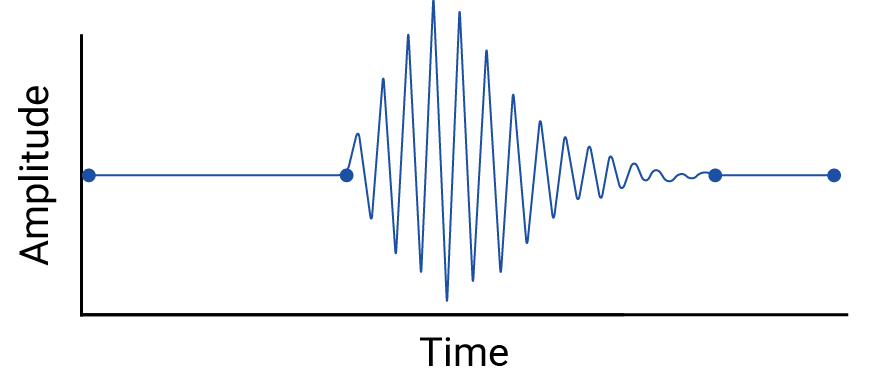
Przykład jest wymyślony, ponieważ sejsmografy zbierają ciągłe dane, więc to trzęsienie nie zostałoby pominięte. Jest ona jednak przydatna do zilustrowania założeń poczynionych na podstawie interpolacji oraz rzeczywistych zjawisk, które mogą umknąć użytkownikom danych.
Zjawisko Runge
Zjawisko Runge'a, zwane też „sprężynowaniem wielomianowym”, to problem leżący po przeciwnej stronie spektrum niż interpolacja liniowa i uwarstwienie liniowe. Podczas dopasowywania interpolacji wielomianowej do danych można użyć wielomianu o zbyt wysokim stopniu (stopień, czyli najwyższy wykładnik w równaniu wielomianowym). Powoduje to dziwne drgania na krawędziach. Na przykład zastosowanie interpolacji wielomianowej stopnia 11, co oznacza, że najwyższy współczynnik w równaniu wielomianowym ma wartość \(x^{11}\), do danych w przybliżeniu liniowych powoduje bardzo złe prognozy na początku i na końcu zakresu danych:
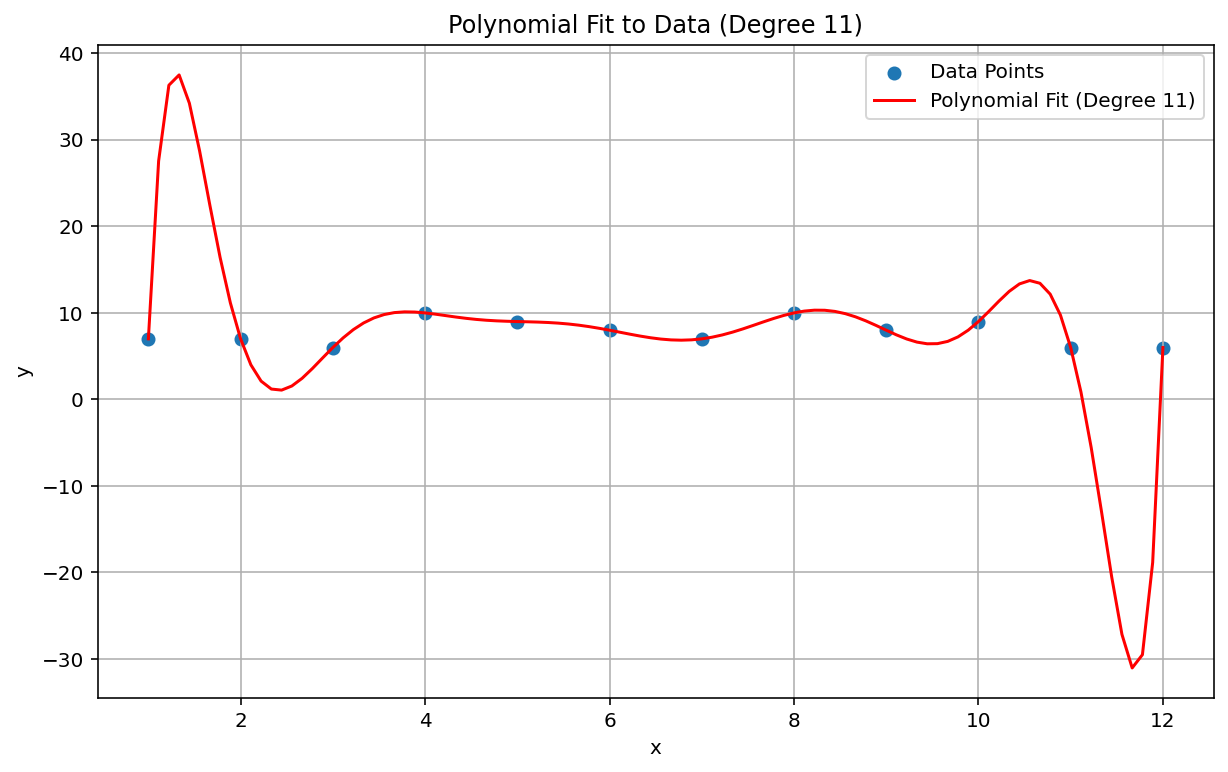
W kontekście uczenia maszynowego analogicznym zjawiskiem jest nadmierne dopasowanie.
Błędy statystyczne do wykrycia
Czasami test statystyczny może być zbyt słaby, aby wykryć niewielki efekt. Niska skuteczność analizy statystycznej oznacza małą szansę na prawidłowe zidentyfikowanie prawdziwych zdarzeń, a co za tym idzie, dużą szansę na fałszywie ujemne wyniki. Katherine Button i współautorzy w czasopiśmie Nature napisali: „Jeśli badania w danym obszarze są zaprojektowane z mocą 20%, oznacza to, że jeśli w danym obszarze jest 100 rzeczywistych efektów niezerowych, badania te powinny wykryć tylko 20 z nich”. Czasami pomocne może być zwiększenie wielkości próbki lub staranne zaprojektowanie badania.
Analogiczna sytuacja w ML to problem klasyfikacji i wyboru progu klasyfikacji. Wybór wyższego progu skutkuje mniejszą liczbą wyników fałszywie pozytywnych i większą liczbą wyników fałszywie negatywnych, a wybór niższego progu skutkuje większą liczbą wyników fałszywie pozytywnych i mniejszą liczbą wyników fałszywie negatywnych.
Oprócz problemów z mocą statystyczną, korelacja jest przeznaczona do wykrywania zależności liniowych, więc nie można wykryć korelacji nieliniowych między zmiennymi. Podobnie zmienne mogą być powiązane ze sobą, ale nie muszą być ze sobą skorelowane statystycznie. Zmienne mogą też mieć ujemną korelację, ale nie mieć ze sobą żadnego związku. Jest to tzw. paradoks Berksona lub błąd Berksona. Klasycznym przykładem błędu Berksona jest pozorna ujemna korelacja między dowolnym czynnikiem ryzyka a ciężką chorobą wśród pacjentów hospitalizowanych (w porównaniu z ogółem populacji), która wynika z procesu selekcji (stan tak ciężki, że wymaga hospitalizacji).
Zastanów się, czy któraś z tych sytuacji Cię dotyczy.
Nieaktualne modele i nieprawidłowe założenia
Nawet dobre modele mogą z czasem tracić na jakości, ponieważ zachowania (i świat) mogą się zmieniać. Wczesne modele predykcyjne Netflixa musiały zostać wycofane, ponieważ baza klientów zmieniła się z młodych, zaawansowanych technologicznie użytkowników na ogół społeczeństwa.10
Modele mogą też zawierać niejawne i nieprecyzyjne założenia, które mogą pozostać ukryte do czasu katastrofalnego załamania modelu, jak w przypadku krachu na rynku w 2008 r. Modele wartości ryzyka (VaR) w branży finansowej miały precyzyjnie szacować maksymalną stratę w portfolio każdego tradera, np. maksymalną stratę 100 tys.USD w 99% przypadków. Jednak w nietypowych warunkach krachu portfele o spodziewanej maksymalnej stracie 100 tys. USD czasami tracą 1 mln USD lub więcej.
Modele VaR były oparte na błędnych założeniach, takich jak:
- Poprzednie zmiany na rynku przewidują przyszłe zmiany na rynku.
- Przewidywane zwroty były oparte na rozkładzie normalnym (z wąskim ogonem, a więc przewidywalnym).
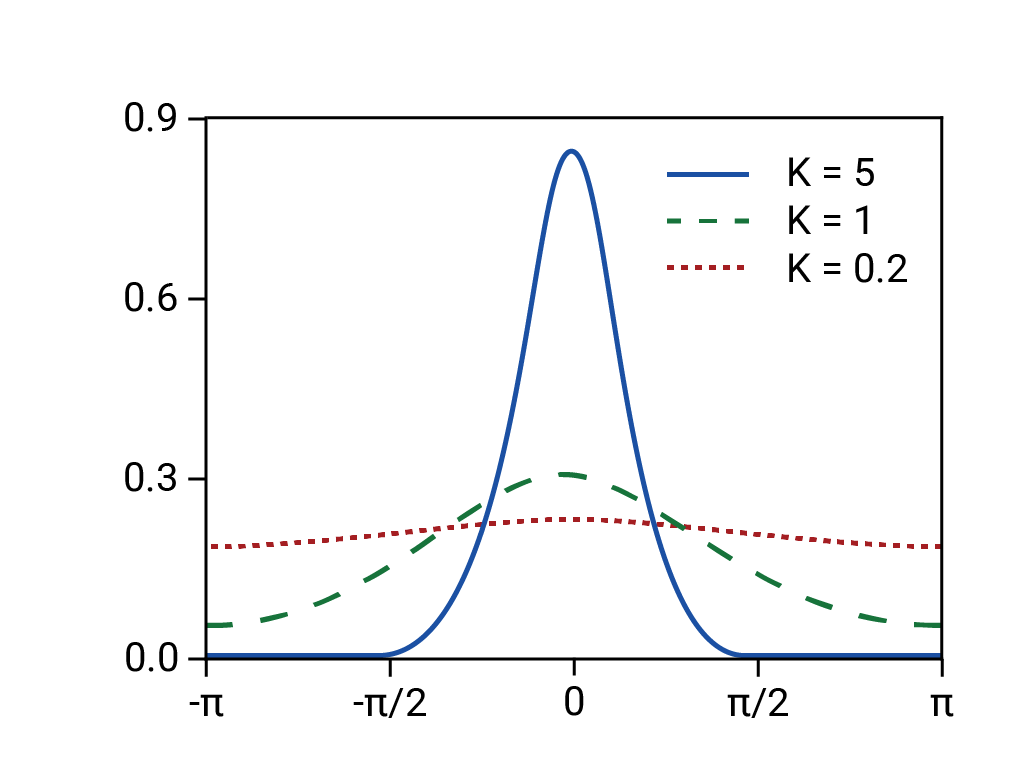
W istocie rozkład był rozkładem o grubych ogonach, „dzikim” lub fraktalnym, co oznacza, że ryzyko wystąpienia rzadkich, ekstremalnych zdarzeń o długich ogonach było znacznie większe niż przewidywałby to rozkład normalny. Charakterystyka rozkładu o grubych ogonach była dobrze znana, ale nie podjęto żadnych działań. Mniej znane były natomiast złożoność i ścisłe powiązanie różnych zjawisk, w tym handlu opartego na komputerach z automatycznymi wyprzedażami.11
Problemy z agregacją
Dane agregowane, które obejmują większość danych demograficznych i epidemiologicznych, są podatne na określone pułapki. Paradoks Simpsona, czyli paradoks akumulacji, występuje w przypadku danych zbiorczych, w których widoczne trendy znikają lub odwracają się, gdy dane są agregowane na innym poziomie z powodu czynników zakłócających i niepoprawnych relacji przyczynowych.
Błąd ekologiczny polega na błędnym ekstrapolowaniu informacji o populacji na jednym poziomie agregacji na inny poziom agregacji, gdzie twierdzenie może być nieprawidłowe. Choroba, która dotyka 40% pracowników rolnych w jednej prowincji, może nie występować wśród większej populacji. Bardzo prawdopodobne jest też, że w tej prowincji będą się znajdować pojedyncze farmy lub miasta rolnicze, w których nie będzie występować tak wysoka zapadalność na tę chorobę. Zakładanie, że 40% występowania w tych mniej dotkniętych miejscach jest błędne.
Problem modyfikowalnej jednostki obszarowej (MAUP) to znany problem z danymi geoprzestrzennymi, opisany przez Stana Openshawa w 1984 roku w artykule CATMOG 38. W zależności od kształtów i rozmiarów obszarów używanych do agregacji danych specjalista ds. danych geoprzestrzennych może ustalić niemal dowolną korelację między zmiennymi w danych. Wyznaczanie okręgów wyborczych, które faworyzują jedną partię lub drugą, jest przykładem naruszenia zasady MAUP.
Wszystkie te sytuacje dotyczą nieprawidłowej ekstrapolacji z jednego poziomu agregacji na inny. Różne poziomy analizy mogą wymagać różnych agregacji, a nawet zupełnie innych zbiorów danych.12
Pamiętaj, że dane z spisów ludności, dane demograficzne i epidemiologiczne są zwykle agregowane według stref ze względów związanych z ochroną prywatności, a strefy te są często umowne, co oznacza, że nie są oparte na istotnych granicach w rzeczywistych warunkach. Pracując z tymi typami danych, specjaliści w zakresie uczenia maszynowego powinni sprawdzić, czy skuteczność modelu i jego przewidywania zmieniają się w zależności od rozmiaru i kształtu wybranych stref lub poziomu agregacji, a jeśli tak, to czy na przewidywaniach modelu wpływa jedno z tych problemów z agregacją.
Odniesienia
Button, Katharine i inni. „Power failure: why small sample size undermines the reliability of neuroscience." Nature Reviews Neuroscience, vol. 14 (2013), 365–376. DOI: https://doi.org/10.1038/nrn3475
Alberto z Kairu. How Charts Lie: Getting Smarter about Visual Information (Jak kłamią wykresy: jak mądrze korzystać z wizualnych informacji). NY: W.W. Norton, 2019.
Davenport, Thomas H. „A Predictive Analytics Primer” HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), s. 81–86.
De Langhe, Bart, Stefano Puntoni i Richard Larrick. „Linear Thinking in a Non-Linear World” HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), s. 131–154.
Ellenberg, Jordan. How Not to Be Wrong: The Power of Mathematical Thinking NY: Penguin, 2014.
Huff, Darrell. How to Lie with Statistics (Jak kłamać za pomocą statystyk). NY: W.W. Norton, 1954.
Jones, Ben. Unikanie pułapek związanych z danymi Hoboken, NJ: Wiley, 2020.
Openshaw, Stan. „The Modifiable Areal Unit Problem”, CATMOG 38 (Norwich, England: Geo Books 1984) 37.
The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) (testimonies of Nassim N. Taleb i Richard Bookstaber).
Ritter, David. „When to Act on a Correlation, and When Not To” HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), 103–109.
Tulchinsky, Theodore H. i Elena A. Varavikova. „Rozdział 3. Pomiar, monitorowanie i ocena zdrowia populacji” w książce Nowa epidemiologia (3 wyd.), San Diego: Academic Press, 2014, s. 91–147. DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.
Van Doorn, Jenny, Peter C. Verhoef i Tammo H. A. Bijmolt. „Znaczenie nieliniowych relacji między postawą a zachowaniem w badaniach nad polityką”. Journal of Consumer Policy 30 (2007) 75–90. DOI: https://doi.org/10.1007/s10603-007-9028-3
Odniesienie do obrazu
Na podstawie „Von Mises Distribution”. Rainald62, 2018. Źródło
-
Ellenberg 125. ↩
-
Huff 77-79. Huff powołuje się na biuro badań opinii publicznej Uniwersytetu Princeton, ale może mieć na myśli raport z kwietnia 1944 r. Centrum badań opinii publicznej Uniwersytetu w Denver. ↩
-
Tulchinsky i Varavikova. ↩
-
Gary Taubes, Do We Really Know What Makes Us Healthy?" w The New York Times Magazine, 16 września 2007 r. ↩
-
Ellenberg 78. ↩
-
Huff 91-92. ↩
-
Huff 93. ↩
-
Jones 157-167. ↩
-
Huff 95. ↩
-
Davenport 84. ↩
-
Zobacz zeznania Nassima N. Taleb i Richard Bookstaber w The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) 11-67. ↩
-
Kair 155, 162. ↩