"ทุกรูปแบบผิดหมด แต่บางรูปแบบมีประโยชน์" — George Box, 1978
แม้ว่าเทคนิคทางสถิติจะมีประสิทธิภาพ แต่ก็มีข้อจํากัด การทำความเข้าใจข้อจำกัดเหล่านี้จะช่วยให้นักวิจัยหลีกเลี่ยงความผิดพลาดและการกล่าวอ้างที่ไม่ถูกต้องได้ เช่น ความเห็นของ BF Skinner ที่ว่า Shakespeare ไม่ได้ใช้การซ้ำคำมากกว่าที่ความน่าจะเป็นแบบสุ่มจะคาดการณ์ไว้ (การศึกษาของ Skinner มีจำนวนตัวอย่างไม่เพียงพอ1)
ความไม่แน่นอนและแถบข้อผิดพลาด
คุณควรระบุความไม่แน่นอนในการวิเคราะห์ การประเมินความไม่แน่นอนในการวิเคราะห์ของผู้อื่นก็สำคัญไม่แพ้กัน จุดข้อมูลที่ดูเหมือนจะแสดงแนวโน้มในกราฟ แต่มีแถบข้อผิดพลาดที่ทับซ้อนกันอาจไม่ได้บ่งบอกถึงรูปแบบใดๆ เลย นอกจากนี้ ความไม่แน่นอนอาจสูงเกินกว่าที่จะสรุปข้อมูลที่เป็นประโยชน์จากการศึกษาหรือการทดสอบทางสถิติหนึ่งๆ ได้ หากการศึกษาวิจัยต้องใช้ความแม่นยำระดับแปลง ชุดข้อมูลเชิงพื้นที่ที่มีความไม่แน่นอน +/- 500 ม. จะมีความไม่แน่นอนมากเกินไปที่จะใช้งานได้
หรือระดับความไม่แน่นอนอาจมีประโยชน์ในระหว่างกระบวนการตัดสินใจ ข้อมูลสนับสนุนการบำบัดน้ำแบบใดแบบหนึ่งที่มีความไม่แน่นอน 20% ในผลลัพธ์อาจนำไปสู่คําแนะนําในการใช้การบำบัดน้ำนั้นโดยต้องติดตามผลโปรแกรมอย่างต่อเนื่องเพื่อจัดการกับความไม่แน่นอนดังกล่าว
เครือข่ายประสาทแบบเบย์เซียนสามารถวัดความไม่แน่นอนโดยการคาดการณ์การแจกแจงค่าแทนค่าเดี่ยว
ไม่เกี่ยวข้อง
ดังที่ได้กล่าวไว้ในบทนำ ข้อมูลและความเป็นจริงมักจะมีความคลาดเคลื่อนกันอยู่บ้าง ผู้ปฏิบัติงาน ML ที่ฉลาดควรพิจารณาว่าชุดข้อมูลมีความเกี่ยวข้องกับคำถามที่ถามหรือไม่
Huff อธิบายการศึกษาความคิดเห็นสาธารณะในช่วงแรกๆ ซึ่งพบว่าคำตอบของชาวอเมริกันผิวขาวสำหรับคำถามที่ว่าชาวอเมริกันผิวดำหาเลี้ยงชีพได้ง่ายเพียงใดนั้นสัมพันธ์กับระดับความเห็นอกเห็นใจชาวอเมริกันผิวดำโดยตรงและในทางกลับกัน เมื่อความเกลียดชังทางเชื้อชาติเพิ่มขึ้น คำตอบเกี่ยวกับโอกาสทางเศรษฐกิจที่คาดหวังก็มีความหวังมากขึ้น ซึ่งอาจทำให้เข้าใจผิดว่าเป็นสัญญาณของความคืบหน้า อย่างไรก็ตาม การศึกษานี้ไม่สามารถแสดงข้อมูลเกี่ยวกับโอกาสทางเศรษฐกิจที่แท้จริงที่ชาวอเมริกันผิวดำมีในขณะนั้น และก็ไม่เหมาะที่จะใช้สรุปเกี่ยวกับความเป็นจริงของตลาดงาน มีเพียงความคิดเห็นของผู้ตอบแบบสํารวจเท่านั้น ข้อมูลที่รวบรวมมานั้นไม่เกี่ยวข้องกับสภาพตลาดงานจริง2
คุณสามารถฝึกโมเดลด้วยข้อมูลแบบสํารวจตามที่อธิบายไว้ข้างต้น ซึ่งเอาต์พุตจะวัดความเชื่อมั่น ไม่ใช่โอกาส แต่เนื่องจากโอกาสที่คาดการณ์ไม่เกี่ยวข้องกับโอกาสที่เกิดขึ้นจริง หากคุณกล่าวอ้างว่าโมเดลคาดการณ์โอกาสที่เกิดขึ้นจริง แสดงว่าคุณสื่อให้เข้าใจผิดเกี่ยวกับสิ่งที่โมเดลคาดการณ์
ปัจจัยที่ทำให้สับสน
ตัวแปรที่ก่อความสับสน ความสับสน หรือปัจจัยร่วมคือตัวแปรที่ไม่ได้อยู่ภายใต้การศึกษาซึ่งส่งผลต่อตัวแปรที่อยู่ภายใต้การศึกษาและอาจบิดเบือนผลลัพธ์ ตัวอย่างเช่น ลองพิจารณาโมเดล ML ที่คาดการณ์อัตราการตายของประเทศอินพุตตามฟีเจอร์นโยบายด้านสาธารณสุข สมมติว่าค่ามัธยฐานอายุไม่ใช่ฟีเจอร์ สมมติเพิ่มเติมว่าบางประเทศมีประชากรที่มีอายุมากกว่าประเทศอื่นๆ การละเว้นตัวแปรที่ทำให้เกิดความสับสนเกี่ยวกับอายุมัธยฐานอาจทําให้โมเดลนี้คาดการณ์อัตราการตายที่ไม่ถูกต้อง
ในสหรัฐอเมริกา เชื้อชาติมักมีความสัมพันธ์อย่างมากกับชนชั้นทางสังคมและเศรษฐกิจ แม้ว่าจะมีบันทึกเฉพาะเชื้อชาติเท่านั้น ไม่ใช่ชนชั้น ไว้กับข้อมูลการเสียชีวิต ปัจจัยที่ทำให้เกิดความสับสนที่เกี่ยวข้องกับชนชั้น เช่น การเข้าถึงบริการสาธารณสุข โภชนาการ การทำงานที่มีอันตราย และที่อยู่อาศัยที่ปลอดภัย อาจส่งผลต่ออัตราการเสียชีวิตมากกว่าเชื้อชาติ แต่กลับถูกละเลยเนื่องจากไม่ได้รวมอยู่ในชุดข้อมูล3 การระบุและควบคุมปัจจัยเหล่านี้มีความสําคัญต่อการสร้างโมเดลที่มีประโยชน์และดึงข้อสรุปที่ถูกต้องและสมเหตุสมผล
หากโมเดลได้รับการฝึกจากข้อมูลการเสียชีวิตที่มีอยู่ ซึ่งรวมถึงเชื้อชาติแต่ไม่รวมถึงชนชั้น โมเดลอาจคาดการณ์การเสียชีวิตตามเชื้อชาติ แม้ว่าชนชั้นจะเป็นตัวทำนายการเสียชีวิตที่แม่นยำกว่าก็ตาม ซึ่งอาจทําให้มีข้อสันนิษฐานที่ไม่ถูกต้องเกี่ยวกับสาเหตุและการคาดการณ์ที่ไม่ถูกต้องเกี่ยวกับอัตราการตายของผู้ป่วย ผู้ปฏิบัติงานด้าน ML ควรถามว่าข้อมูลของตนมีปัจจัยที่ทำให้สับสนหรือไม่ รวมถึงดูว่าชุดข้อมูลขาดตัวแปรที่มีความหมายใดไปบ้าง
ในปี 1985 การศึกษาสุขภาพของพยาบาล ซึ่งเป็นการศึกษาแบบสังเกตการณ์ตามกลุ่มประชากรจากคณะแพทยศาสตร์ฮาร์วาร์ดและคณะสาธารณสุขศาสตร์ฮาร์วาร์ด พบว่าสมาชิกกลุ่มประชากรที่ใช้การบำบัดด้วยเอสโตรเจนทดแทนมีอัตราการเกิดโรคหัวใจวายต่ำกว่าเมื่อเทียบกับสมาชิกกลุ่มประชากรที่ไม่เคยใช้เอสโตรเจน ด้วยเหตุนี้ แพทย์จึงสั่งจ่ายเอสโตรเจนให้กับคนไข้วัยหมดประจำเดือนและวัยหลังหมดประจำเดือนมานานหลายทศวรรษ จนกระทั่งการศึกษาทางคลินิกในปี 2002 ระบุถึงความเสี่ยงต่อสุขภาพที่เกิดจากการบำบัดด้วยเอสโตรเจนในระยะยาว การใช้ฮอร์โมนเอสโตรเจนกับผู้หญิงวัยหมดประจำเดือนหยุดลงแล้ว แต่ก่อนที่จะหยุดลง ฮอร์โมนดังกล่าวได้ทําให้ผู้คนเสียชีวิตก่อนวัยอันควรหลายหมื่นคน
ปัจจัยหลายอย่างที่ทำให้เกิดความสับสนอาจทำให้เกิดความสัมพันธ์นี้ นักระบาดวิทยาพบว่าผู้หญิงที่ใช้การบำบัดด้วยฮอร์โมนทดแทนมีแนวโน้มที่จะผอมกว่า เรียนจบมากกว่า มีเงินมากกว่า ใส่ใจสุขภาพมากกว่า และออกกำลังกายมากกว่าเมื่อเทียบกับผู้หญิงที่ไม่ได้ใช้ จากการศึกษาต่างๆ พบว่าการศึกษาและความมั่งคั่งช่วยลดความเสี่ยงของโรคหัวใจ ผลข้างเคียงเหล่านี้อาจทำให้ความสัมพันธ์ที่ชัดเจนระหว่างการรักษาด้วยเอสโตรเจนกับโรคหัวใจ4เกิดความสับสน
เปอร์เซ็นต์ที่มีตัวเลขติดลบ
หลีกเลี่ยงการใช้เปอร์เซ็นต์เมื่อมีตัวเลขติดลบ5 เนื่องจากอาจทำให้การเพิ่มขึ้นและการลดลงที่มีความหมายทุกประเภทถูกบดบัง สมมติว่าอุตสาหกรรมร้านอาหารมีงาน 2 ล้านตำแหน่งเพื่อให้คำนวณได้ง่าย หากอุตสาหกรรมสูญเสียงานดังกล่าว 1 ล้านตำแหน่งในช่วงปลายเดือนมีนาคม 2020 ไม่มีการเปลี่ยนแปลงสุทธิเป็นเวลา 10 เดือน และได้รับงานกลับคืนมา 900,000 ตำแหน่งในช่วงต้นเดือนกุมภาพันธ์ 2021 การเปรียบเทียบปีต่อปีในช่วงต้นเดือนมีนาคม 2021 จะแสดงให้เห็นว่างานในร้านอาหารหายไปเพียง 5% หากไม่มีการเปลี่ยนแปลงอื่นๆ การเปรียบเทียบปีต่อปีในช่วงสิ้นเดือนเมษายน 2021 จะแสดงให้เห็นว่ามีงานในร้านอาหารเพิ่มขึ้น 90% ซึ่งแตกต่างอย่างมากจากความเป็นจริง
ใช้ตัวเลขจริงที่ปรับให้เป็นมาตรฐานตามความเหมาะสม ดูข้อมูลเพิ่มเติมได้ที่การทํางานกับข้อมูลตัวเลข
ข้อผิดพลาดแบบหลังเกิดและความสัมพันธ์ที่ใช้งานไม่ได้
ข้อผิดพลาดแบบหลังเกิดคือการสันนิษฐานว่าเหตุการณ์ ก. เป็นสาเหตุของเหตุการณ์ ข. เนื่องจากเหตุการณ์ ก. เกิดขึ้นก่อนเหตุการณ์ ข. กล่าวอย่างง่ายคือ การกล่าวเป็นนัยถึงความสัมพันธ์แบบสาเหตุและผลซึ่งไม่มีอยู่จริง พูดให้เข้าใจง่ายกว่านั้นคือ ความสัมพันธ์ไม่ได้พิสูจน์ความเป็นเหตุเป็นผล
นอกจากความสัมพันธ์แบบสาเหตุและผลที่ชัดเจนแล้ว ความสอดคล้องอาจเกิดจากสาเหตุต่อไปนี้ด้วย
- เกิดจากความบังเอิญล้วนๆ (ดูภาพประกอบจากบทความความสัมพันธ์ที่ไม่สอดคล้องกันของ Tyler Vigen ซึ่งรวมถึงความสัมพันธ์ที่แน่นแฟ้นระหว่างอัตราการหย่าในรัฐเมนกับการบริโภคมาการีน)
- ความสัมพันธ์จริงระหว่างตัวแปร 2 ตัว แม้ว่าจะยังไม่ชัดเจนว่าตัวแปรใดเป็นสาเหตุและตัวแปรใดได้รับผลกระทบ
- สาเหตุที่ 3 แยกต่างหากซึ่งส่งผลต่อทั้ง 2 ตัวแปร แม้ว่าตัวแปรที่เกี่ยวข้องจะไม่เกี่ยวข้องกันก็ตาม ตัวอย่างเช่น เงินเฟ้อทั่วโลกอาจทำให้ทั้งราคาเรือยอชต์และขึ้นฉ่ายสูงขึ้น6
นอกจากนี้ การคาดการณ์ความสัมพันธ์จากข้อมูลที่มีอยู่ก็ยังมีความเสี่ยงด้วย Huff ชี้ว่าฝนตกเล็กน้อยจะช่วยเพิ่มผลผลิต แต่ฝนตกมากเกินไปจะทําให้ผลผลิตลดลง ความสัมพันธ์ระหว่างฝนตกกับผลผลิตของพืชจึงไม่ใช่ความสัมพันธ์เชิงเส้น7 (ดูข้อมูลเพิ่มเติมเกี่ยวกับความสัมพันธ์ที่ไม่ใช่เชิงเส้นได้ในส่วนถัดไป) Jones ระบุว่าโลกเต็มไปด้วยเหตุการณ์ที่ไม่อาจคาดเดาได้ เช่น สงครามและความอดอยาก ซึ่งทำให้การคาดการณ์ข้อมูลอนุกรมเวลาในอนาคตมีความไม่แน่นอนอย่างมาก8
นอกจากนี้ แม้แต่ความสัมพันธ์ที่แท้จริงซึ่งอิงตามเหตุและผลก็อาจไม่เป็นประโยชน์ต่อการตัดสินใจ ตัวอย่างเช่น Huff ยกตัวอย่างความสัมพันธ์ระหว่างความสามารถในการแต่งงานกับการศึกษาระดับวิทยาลัยในปี 1950 ผู้หญิงที่เรียนมหาวิทยาลัยมีแนวโน้มที่จะแต่งงานน้อยกว่า แต่อาจเป็นเพราะผู้หญิงที่เรียนมหาวิทยาลัยมีแนวโน้มที่จะแต่งงานน้อยกว่าตั้งแต่แรก หากเป็นเช่นนั้น การศึกษาระดับวิทยาลัยจะไม่เปลี่ยนแนวโน้มการแต่งงาน9
หากการวิเคราะห์ตรวจพบความสัมพันธ์ระหว่างตัวแปร 2 ตัวในชุดข้อมูล ให้ถามดังนี้
- ความสัมพันธ์ดังกล่าวเป็นความสัมพันธ์แบบใด เช่น ความสัมพันธ์แบบเป็นเหตุเป็นผล ความสัมพันธ์ที่ไม่น่าเชื่อถือ ความสัมพันธ์ที่ไม่รู้จัก หรือเกิดจากตัวแปรที่สาม
- การประมาณจากข้อมูลมีความเสี่ยงมากน้อยเพียงใด การคาดการณ์ของโมเดลทั้งหมดเกี่ยวกับข้อมูลซึ่งไม่ได้อยู่ในชุดข้อมูลการฝึก คือการประมาณหรือการคาดการณ์จากข้อมูล
- สามารถใช้ความสัมพันธ์นี้เพื่อทําการตัดสินใจที่เป็นประโยชน์ได้ไหม ตัวอย่างเช่น ความเชื่อมั่นอาจสัมพันธ์กับค่าจ้างที่เพิ่มขึ้นอย่างมาก แต่การวิเคราะห์ความรู้สึกของข้อมูลข้อความจำนวนมาก เช่น โพสต์โซเชียลมีเดียของผู้ใช้ในประเทศหนึ่งๆ จะไม่เป็นประโยชน์ต่อการคาดการณ์การเพิ่มขึ้นของค่าจ้างในประเทศนั้น
เมื่อฝึกโมเดล ผู้เชี่ยวชาญด้าน ML มักจะมองหาฟีเจอร์ที่มีความเชื่อมโยงกับป้ายกำกับอย่างมาก หากไม่เข้าใจความสัมพันธ์ระหว่างฟีเจอร์กับป้ายกํากับอย่างถ่องแท้ อาจทําให้เกิดปัญหาที่อธิบายไว้ในส่วนนี้ รวมถึงรูปแบบที่อิงตามความสัมพันธ์ที่ไม่ถูกต้องและรูปแบบที่ถือว่าแนวโน้มที่ผ่านมาจะยังคงอยู่ในอนาคต แต่จริงๆ แล้วไม่ใช่เช่นนั้น
ความลำเอียงเชิงเส้น
ในบทความ"การคิดแบบเส้นตรงในโลกที่ไม่เป็นไปตามเส้นตรง" Bart de Langhe, Stefano Puntoni และ Richard Larrick อธิบายความลำเอียงแบบเส้นตรงว่าเป็นแนวโน้มของสมองมนุษย์ที่จะคาดหวังและมองหาความสัมพันธ์แบบเส้นตรง แม้ว่าปรากฏการณ์หลายอย่างจะไม่ใช่แบบเส้นตรงก็ตาม ตัวอย่างเช่น ความสัมพันธ์ระหว่างทัศนคติและพฤติกรรมของมนุษย์คือเส้นโค้งนูนและไม่ใช่เส้นตรง ในบทความของ Journal of Consumer Policy ปี 2007 ที่ de Langhe และคณะอ้างอิง Jenny van Doorn และคณะได้จำลองความสัมพันธ์ระหว่างความกังวลเกี่ยวกับสิ่งแวดล้อมของผู้ตอบแบบสํารวจกับการซื้อผลิตภัณฑ์ออร์แกนิกของผู้ตอบ ผู้ที่มีความกังวลเกี่ยวกับสิ่งแวดล้อมมากที่สุดซื้อผลิตภัณฑ์ออร์แกนิกมากกว่า แต่ผู้ตอบที่เหลือมีความแตกต่างเพียงเล็กน้อย
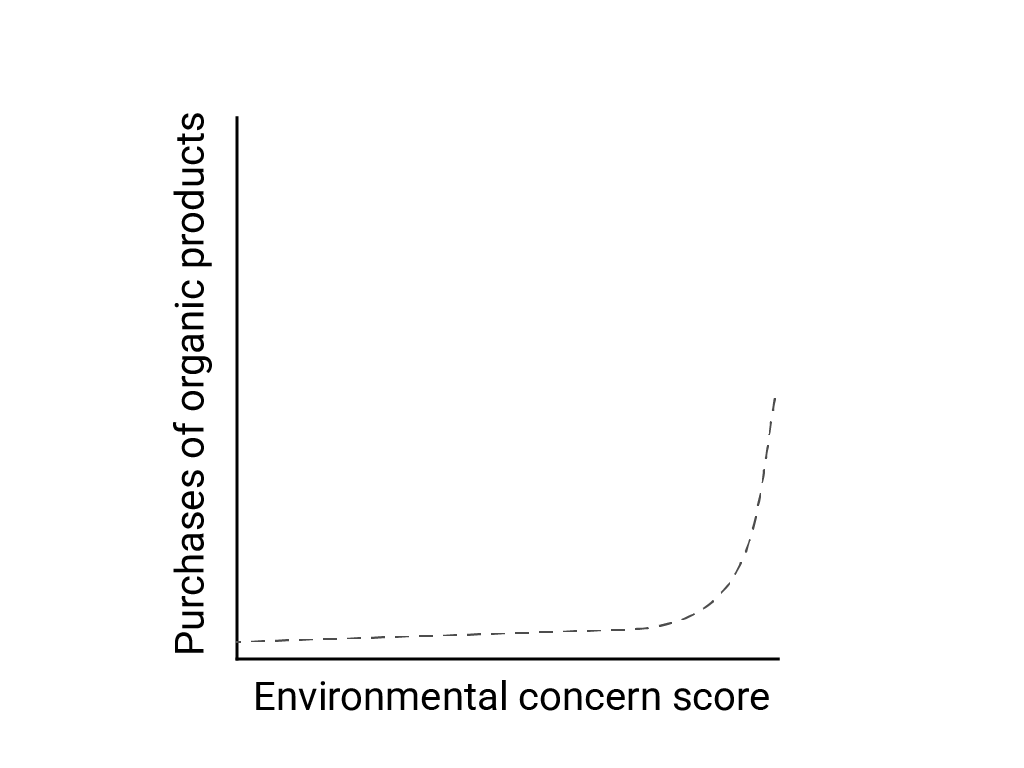
เมื่อออกแบบโมเดลหรือการศึกษา ให้พิจารณาความเป็นไปได้ของความสัมพันธ์ที่ไม่ใช่เชิงเส้น เนื่องจากการทดสอบ A/B อาจพลาดความสัมพันธ์ที่ไม่ใช่เชิงเส้น ให้ลองทดสอบเงื่อนไขที่ 3 ซึ่งเป็นเงื่อนไขกลางอย่าง ค ด้วย นอกจากนี้ ให้พิจารณาด้วยว่าพฤติกรรมเริ่มต้นที่ดูเหมือนเชิงเส้นจะยังคงเป็นเชิงเส้นต่อไปหรือไม่ หรือข้อมูลในอนาคตอาจแสดงลักษณะเชิงลําดับเลขฐานสิบหรือลักษณะอื่นๆ ที่ไม่ใช่เชิงเส้นมากขึ้น
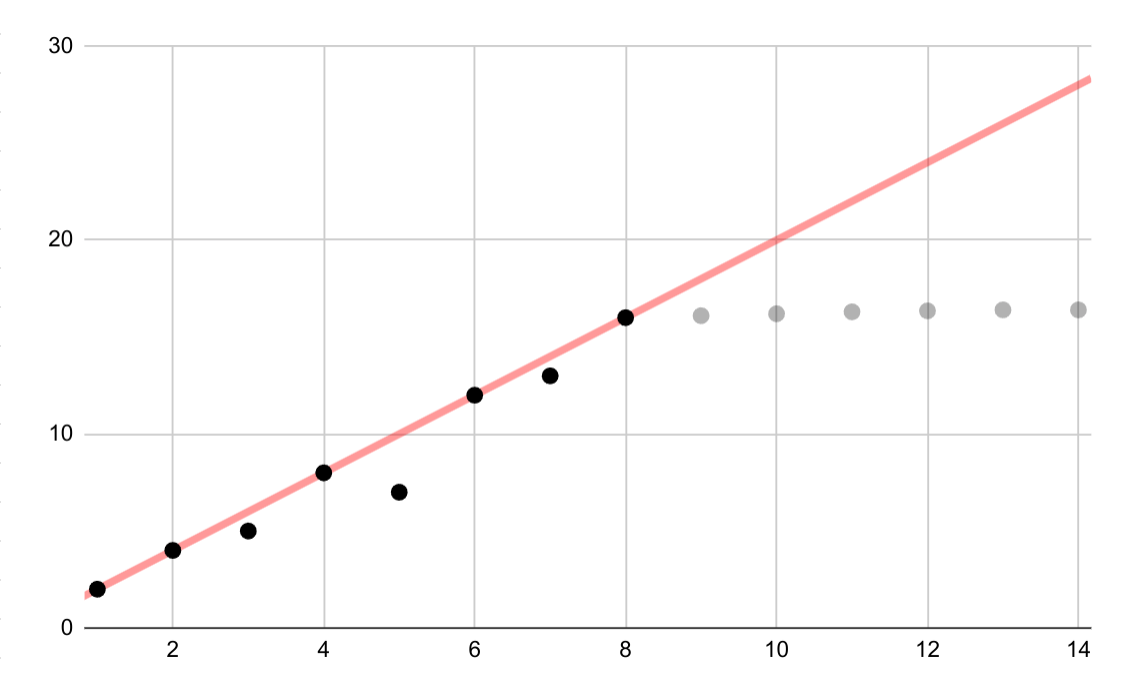
ตัวอย่างสมมตินี้แสดงการประมาณเชิงเส้นที่ไม่ถูกต้องสําหรับข้อมูลเชิงลําดับเลขฐานสิบ หากมีเพียงจุดข้อมูล 2-3 จุดแรกเท่านั้น การพิจารณาว่าตัวแปรมีความสัมพันธ์เชิงเส้นอย่างต่อเนื่องก็เป็นสิ่งที่น่าดึงดูดใจและไม่ถูกต้อง
การประมาณค่าเชิงเส้น
ตรวจสอบการประมาณค่าระหว่างจุดข้อมูล เนื่องจากการประมาณค่าจะนําจุดสมมติมาใช้ และช่วงเวลาระหว่างการวัดจริงอาจมีความผันผวนที่มีความหมาย ตัวอย่างเช่น ลองดูภาพจุดข้อมูล 4 จุดที่เชื่อมต่อกันด้วยการประมาณเชิงเส้นต่อไปนี้

จากนั้นดูตัวอย่างความผันผวนระหว่างจุดข้อมูลที่ลบออกโดยการประมาณค่าเชิงเส้น ดังนี้
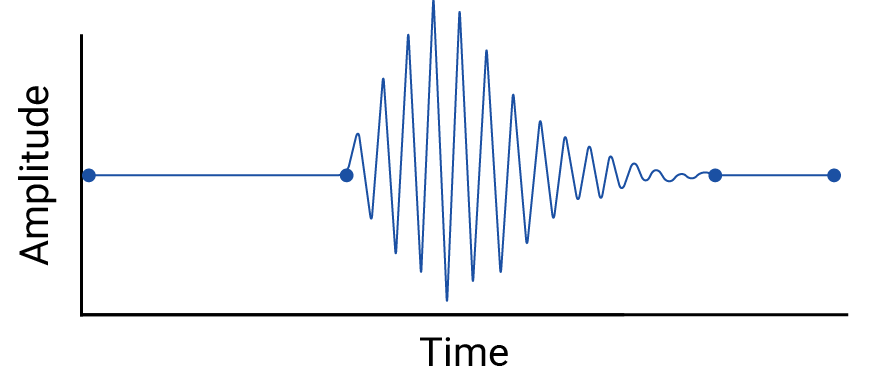
ตัวอย่างนี้เป็นการสมมติขึ้นเนื่องจากเครื่องวัดแผ่นดินไหวจะรวบรวมข้อมูลอย่างต่อเนื่อง ดังนั้นจึงจะไม่พลาดการบันทึกเหตุการณ์แผ่นดินไหวนี้ แต่มีประโยชน์ในการแสดงให้เห็นถึงสมมติฐานที่เกิดจากการแทรกค่า และปรากฏการณ์จริงที่นักปฏิบัติด้านข้อมูลอาจมองข้าม
ปรากฏการณ์ของ Runge
ปรากฏการณ์ของ Runge หรือที่เรียกว่า "การแกว่งแบบพหุนาม" เป็นปัญหาที่ตรงข้ามกับช่วงสเปกตรัมของการประมาณเชิงเส้นและการโน้มเอียงเชิงเส้น เมื่อปรับการประมาณเชิงหลายตัวแปรให้กับข้อมูล คุณอาจใช้พหุนามที่มีดีกรีสูงเกินไปได้ (ดีกรีหรือลําดับคือตัวคูณสูงสุดในสมการพหุนาม) ซึ่งจะทำให้เกิดภาพสั่นที่ขอบ ตัวอย่างเช่น การใช้การประมาณด้วยพหุนามระดับ 11 ซึ่งหมายความว่าเทอมที่มีลําดับสูงสุดในสมการพหุนามมี \(x^{11}\)กับข้อมูลเชิงเส้นโดยประมาณ ส่งผลให้การคาดการณ์ที่จุดเริ่มต้นและจุดสิ้นสุดของช่วงข้อมูลแย่มาก
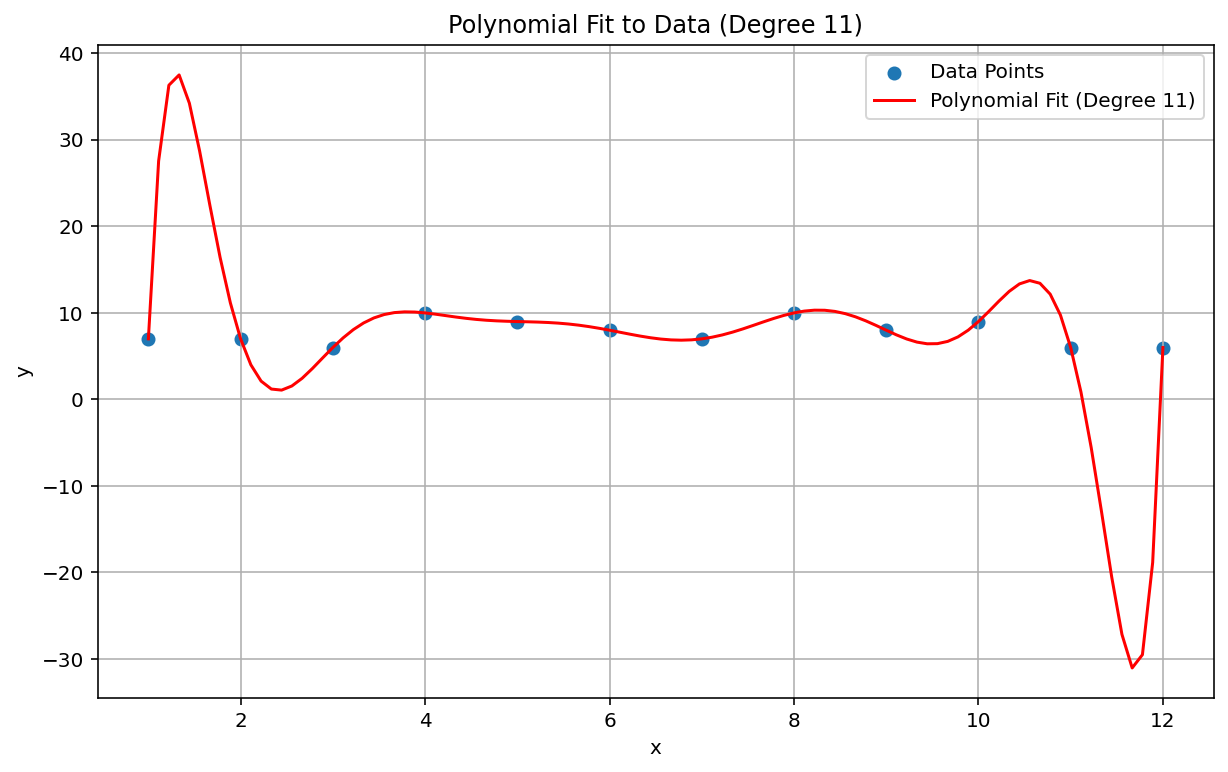
ในบริบทของ ML ปรากฏการณ์ที่คล้ายกันคือการประมาณที่มากเกินไป
ตรวจไม่พบข้อมูลทางสถิติ
บางครั้งการทดสอบทางสถิติอาจไม่มีประสิทธิภาพมากพอที่จะตรวจหาผลลัพธ์เล็กๆ กำลังต่ำในการวิเคราะห์ทางสถิติหมายความว่ามีโอกาสต่ำที่จะระบุเหตุการณ์จริงได้อย่างถูกต้อง จึงมีโอกาสสูงที่จะเกิดผลลบเท็จ Katherine Button และคณะเขียนไว้ใน Nature ว่า "เมื่อการศึกษาในสาขาหนึ่งๆ ได้รับการออกแบบให้มีกำลัง 20% หมายความว่าหากมีผลกระทบที่ไม่ใช่ค่า 0 จริง 100 รายการที่จะค้นพบในสาขานั้น การศึกษาเหล่านี้คาดว่าจะค้นพบเพียง 20 รายการเท่านั้น" บางครั้งการเพิ่มขนาดกลุ่มตัวอย่างอาจช่วยได้ เช่นเดียวกับการออกแบบการศึกษาอย่างรอบคอบ
สถานการณ์ที่คล้ายกันใน ML คือปัญหาการจัดประเภทและการเลือกเกณฑ์การจัดประเภท การเลือกเกณฑ์ที่สูงขึ้นจะส่งผลให้ผลบวกลวงน้อยลงและผลลบลวงมากขึ้น ขณะที่การเลือกเกณฑ์ที่ต่ำลงจะส่งผลให้ผลบวกลวงมากขึ้นและผลลบลวงน้อยลง
นอกเหนือจากปัญหาเกี่ยวกับกำลังทางสถิติแล้ว ความสัมพันธ์ยังออกแบบมาเพื่อตรวจหาความสัมพันธ์เชิงเส้น จึงอาจพลาดความสัมพันธ์ที่ไม่ใช่เชิงเส้นระหว่างตัวแปร ในทํานองเดียวกัน ตัวแปรอาจมีความเกี่ยวข้องกันแต่ไม่ได้มีความเกี่ยวข้องทางสถิติ ตัวแปรยังอาจมีการเชื่อมโยงเชิงลบแต่ไม่มีความสัมพันธ์กันโดยสิ้นเชิง ซึ่งเรียกว่าความขัดแย้งของ Berkson หรือข้อผิดพลาดของ Berkson ตัวอย่างคลาสสิกของข้อผิดพลาดของ Berkson คือความสัมพันธ์เชิงลบที่ไม่ถูกต้องระหว่างปัจจัยเสี่ยงกับโรคร้ายแรงเมื่อพิจารณาประชากรผู้ป่วยในโรงพยาบาล (เทียบกับประชากรทั่วไป) ซึ่งเกิดจากกระบวนการคัดเลือก (โรคร้ายแรงมากจนต้องเข้ารับการรักษาในโรงพยาบาล)
พิจารณาว่าสถานการณ์เหล่านี้ตรงกับคุณหรือไม่
โมเดลที่ล้าสมัยและข้อสมมติที่ไม่ถูกต้อง
แม้แต่โมเดลที่ดีก็อาจมีประสิทธิภาพลดลงเมื่อเวลาผ่านไปเนื่องจากพฤติกรรม (และโลก) อาจเปลี่ยนแปลงไป Netflix ต้องเลิกใช้รูปแบบการคาดการณ์ในช่วงแรกเนื่องจากฐานลูกค้าเปลี่ยนจากผู้ใช้อายุน้อยที่เชี่ยวชาญด้านเทคโนโลยีเป็นประชากรทั่วไป10
โมเดลอาจมีสมมติฐานที่ไม่ถูกต้องและซ่อนอยู่ ซึ่งอาจยังคงซ่อนอยู่จนกว่าโมเดลจะประสบปัญหาร้ายแรง เช่น ตลาดตกต่ำในปี 2008 โมเดลมูลค่าที่เสี่ยง (VaR) ของอุตสาหกรรมการเงินอ้างว่าจะประมาณการขาดทุนสูงสุดในพอร์ตโฟลิโอของผู้ซื้อขายได้อย่างแม่นยำ เช่น คาดการณ์ว่าจะเกิดขาดทุนสูงสุด $100,000 99% ของเวลา แต่ภายใต้ภาวะที่ผิดปกติของตลาดที่ตกต่ำ พอร์ตโฟลิโอที่คาดการณ์ว่าจะมีผลขาดทุนสูงสุด $100,000 บางครั้งก็ขาดทุนถึง $1,000,000 ขึ้นไป
โมเดล VaR อิงตามสมมติฐานที่ไม่ถูกต้อง ซึ่งรวมถึงสิ่งต่อไปนี้
- การเปลี่ยนแปลงของตลาดที่ผ่านมาเป็นแนวทางในการคาดการณ์การเปลี่ยนแปลงของตลาดในอนาคต
- ผลตอบแทนที่คาดการณ์ได้มาจากข้อมูลการแจกแจงแบบปกติ (หางบาง จึงคาดการณ์ได้)
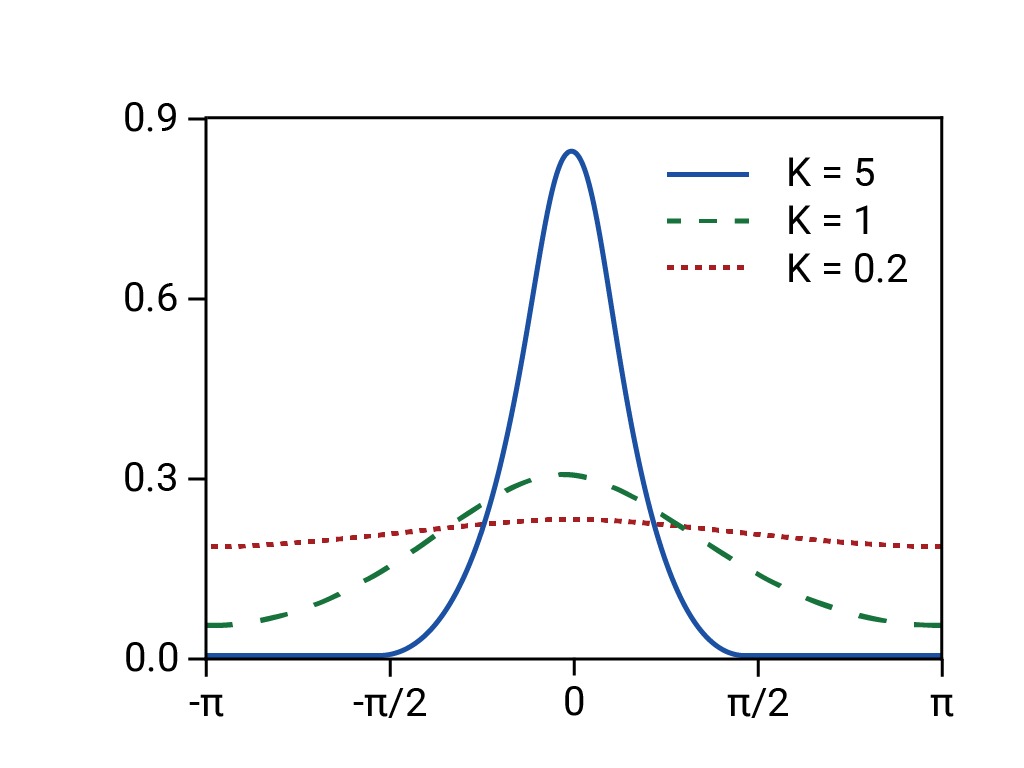
แต่จริงๆ แล้ว ข้อมูลประชากรพื้นฐานคือข้อมูลประชากรที่มีค่าเบี่ยงเบนสูง "ผิดปกติ" หรือแฟรกทัล ซึ่งหมายความว่ามีความเสี่ยงสูงมากที่จะมีเหตุการณ์ที่เกิดขึ้นไม่บ่อย รุนแรง และคาดว่าจะเกิดขึ้นน้อยมาก มากกว่าที่ข้อมูลประชากรปกติจะคาดการณ์ ลักษณะการแจกแจงแบบหางกระจายของข้อมูลจริงนั้นเป็นที่รู้จักกันดี แต่ไม่มีใครดำเนินการใดๆ สิ่งที่ไม่ค่อยมีคนทราบคือความซับซ้อนและความสัมพันธ์ที่เหนียวแน่นของปรากฏการณ์ต่างๆ ซึ่งรวมถึงการซื้อขายด้วยคอมพิวเตอร์ที่มีการขายออกอัตโนมัติ11
ปัญหาการรวม
ข้อมูลที่รวบรวม ซึ่งรวมถึงข้อมูลประชากรและข้อมูลระบาดวิทยาส่วนใหญ่ อยู่ภายใต้ข้อจำกัดบางประการ ความขัดแย้งของซิมป์สัน หรือความขัดแย้งจากการรวมเกิดขึ้นในข้อมูลที่รวบรวมแล้วเมื่อแนวโน้มที่เห็นได้ชัดหายไปหรือกลับกันเมื่อมีการรวบรวมข้อมูลในระดับอื่น เนื่องจากปัจจัยที่ทำให้สับสนและความสัมพันธ์เชิงสาเหตุที่เข้าใจผิด
ข้อผิดพลาดด้านนิเวศวิทยาเกี่ยวข้องกับการคาดการณ์ข้อมูลประชากรในระดับการรวมข้อมูลหนึ่งไปยังอีกระดับการรวมข้อมูลหนึ่งอย่างไม่ถูกต้อง ซึ่งการกล่าวอ้างดังกล่าวอาจไม่ถูกต้อง โรคที่ส่งผลกระทบต่อแรงงานเกษตร 40% ในจังหวัดหนึ่งอาจไม่พบในประชากรจำนวนมากในอัตราเดียวกัน นอกจากนี้ ยังมีความเป็นไปได้สูงที่จะมีฟาร์มหรือเมืองเกษตรกรรมแบบโดดเดี่ยวในจังหวัดนั้นซึ่งไม่ได้ประสบปัญหาการแพร่กระจายของโรคในระดับสูงเช่นเดียวกัน การสันนิษฐานว่าความชุกอยู่ที่ 40% ในสถานที่ที่ได้รับผลกระทบน้อยกว่าก็เป็นการกล่าวอ้างที่ผิดพลาดเช่นกัน
ปัญหาหน่วยพื้นที่ที่ปรับเปลี่ยนได้ (MAUP) เป็นปัญหาที่รู้จักกันดีในข้อมูลเชิงพื้นที่ ซึ่ง Stan Openshaw อธิบายไว้ในปี 1984 ใน CATMOG 38 ผู้เชี่ยวชาญด้านข้อมูลเชิงพื้นที่สามารถสร้างความสัมพันธ์ระหว่างตัวแปรในข้อมูลได้เกือบทุกรูปแบบ โดยขึ้นอยู่กับรูปร่างและขนาดของพื้นที่ที่ใช้รวบรวมข้อมูล การกำหนดเขตเลือกตั้งที่เอื้อประโยชน์ให้พรรคการเมืองหนึ่งๆ เป็นตัวอย่างของ MAUP
สถานการณ์เหล่านี้ทั้งหมดเกี่ยวข้องกับการคาดการณ์ที่ไม่เหมาะสมจากระดับการรวมข้อมูลหนึ่งไปยังอีกระดับหนึ่ง การวิเคราะห์ในระดับต่างๆ อาจต้องใช้การรวมข้อมูลที่แตกต่างกันหรือแม้แต่ชุดข้อมูลที่แตกต่างกันโดยสิ้นเชิง12
โปรดทราบว่าข้อมูลประชากร ข้อมูลประชากร และข้อมูลระบาดวิทยามักจะรวบรวมตามโซนเพื่อเหตุผลด้านความเป็นส่วนตัว และโซนเหล่านี้มักกำหนดขึ้นโดยพลการ ซึ่งหมายความว่าไม่ได้อิงตามขอบเขตที่มีความหมายในชีวิตจริง เมื่อทํางานกับข้อมูลประเภทเหล่านี้ ผู้ปฏิบัติงาน ML ควรตรวจสอบว่าประสิทธิภาพและการคาดการณ์ของโมเดลเปลี่ยนแปลงตามขนาดและรูปร่างของโซนที่เลือกหรือระดับการรวมหรือไม่ และหากเป็นเช่นนั้น การคาดการณ์ของโมเดลจะได้รับผลกระทบจากปัญหาการรวมข้อมูลอย่างใดอย่างหนึ่งเหล่านี้หรือไม่
ข้อมูลอ้างอิง
Button, Katharine et al. "Power failure: why small sample size undermines the reliability of neuroscience." Nature Reviews Neuroscience vol 14 (2013), 365–376. DOI: https://doi.org/10.1038/nrn3475
Cairo, Alberto How Charts Lie: Getting Smarter about Visual Information NY: W.W. Norton, 2019.
Davenport, Thomas H. "ข้อมูลเบื้องต้นเกี่ยวกับข้อมูลวิเคราะห์ตามการคาดการณ์" ใน HBR Guide to Data Analytics Basics for Managers (บอสตัน: HBR Press, 2018) หน้า 81-86
De Langhe, Bart, Stefano Puntoni และ Richard Larrick "การคิดแบบเส้นตรงในโลกที่ไม่เป็นไปตามเส้นตรง" ใน HBR Guide to Data Analytics Basics for Managers (บอสตัน: HBR Press, 2018) 131-154
Ellenberg, Jordan How Not to Be Wrong: The Power of Mathematical Thinking NY: Penguin, 2014.
Huff, Darrell. วิธีโกหกด้วยสถิติ NY: W.W. Norton, 1954.
Jones, Ben. การหลีกเลี่ยงข้อผิดพลาดเกี่ยวกับข้อมูล Hoboken, NJ: Wiley, 2020.
Openshaw, Stan. "The Modifiable Areal Unit Problem," CATMOG 38 (Norwich, England: Geo Books 1984) 37.
ความเสี่ยงของรูปแบบทางการเงิน: VaR และภาวะเศรษฐกิจถดถอย, สภาค 111 (2009) (คำให้การของ Nassim N. Taleb และ Richard Bookstaber)
Ritter, David "เมื่อใดควรดำเนินการตามความสัมพันธ์ และไม่ควรดำเนินการ" ในคู่มือ HBR เกี่ยวกับข้อมูลพื้นฐานด้านการวิเคราะห์ข้อมูลสําหรับผู้จัดการ (บอสตัน: HBR Press, 2018) หน้า 103-109
Tulchinsky, Theodore H. and Elena A. Varavikova "บทที่ 3: การวัดผล การตรวจสอบ และการประเมินสุขภาพของประชากร" ใน The New Public Health, ฉบับที่ 3 San Diego: Academic Press, 2014, หน้า 91-147 DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.
Van Doorn, Jenny, Peter C. Verhoef และ Tammo H. A. Bijmolt "ความสำคัญของความสัมพันธ์แบบไม่เชิงเส้นระหว่างทัศนคติและพฤติกรรมในงานวิจัยด้านนโยบาย" Journal of Consumer Policy 30 (2007) 75–90. DOI: https://doi.org/10.1007/s10603-007-9028-3
รูปภาพอ้างอิง
อิงตาม "การแจกแจง Von Mises" Rainald62, 2018 แหล่งที่มา
-
Ellenberg 125 ↩
-
Huff 77-79 Huff อ้างอิงสำนักงานวิจัยความคิดเห็นสาธารณะของ Princeton แต่เขาอาจนึกถึงรายงานเดือนเมษายน 1944 ของศูนย์วิจัยความคิดเห็นแห่งชาติ (National Opinion Research Center) ที่มหาวิทยาลัยเดนเวอร์ ↩
-
Tulchinsky และ Varavikova ↩
-
Gary Taubes, Do We Really Know What Makes Us Healthy?" ใน The New York Times Magazine วันที่ 16 กันยายน 2007 ↩
-
Ellenberg 78. ↩
-
Huff 91-92 ↩
-
Huff 93 ↩
-
Jones 157-167 ↩
-
Huff 95 ↩
-
Davenport 84 ↩
-
ดูการกล่าวคำให้การต่อสภาคองเกรสของ Nassim N. Taleb และ Richard Bookstaber ในThe Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) 11-67 ↩
-
Cairo 155, 162 ↩