בקטע הזה נסקור את השלבים להכנת נתונים שרלוונטיים ביותר לקיבוץ, מהמודול עבודה עם נתונים מספריים בקורס 'למידת מכונה במהירות'.
בצבירה, כדי לחשב את הדמיון בין שתי דוגמאות, משלבים את כל נתוני המאפיינים של הדוגמאות האלה בערך מספרי. לשם כך, צריך שהמאפיינים יהיו באותו סולם. אפשר להשיג זאת על ידי יצירת נורמלים, טרנספורמציה או יצירת קוינטלים. אם רוצים לבצע טרנספורמציה של הנתונים בלי לבדוק את ההפצה שלהם, אפשר להגדיר כברירת מחדל את הערכים של הרבעונים.
נורמליזציה של נתונים
כדי להעביר נתונים של כמה מאפיינים לאותו סולם, אפשר לנרמל את הנתונים.
ציונים Z
בכל פעם שמופיע מערך נתונים שנראה בערך כמו חלוקה נורמלית, צריך לחשב את ציוני ה-z של הנתונים. ציונים Z הם מספר סטיות התקן של ערך מהממוצע. אפשר להשתמש גם במדדי z כאשר מערך הנתונים לא גדול מספיק לחישוב קוטילים.
במאמר שינוי קנה מידה לפי ציון Z מוסבר איך עושים את זה.
לפניכם תצוגה חזותית של שתי תכונות של מערך נתונים לפני ואחרי שינוי הסולם לפי ציון z:
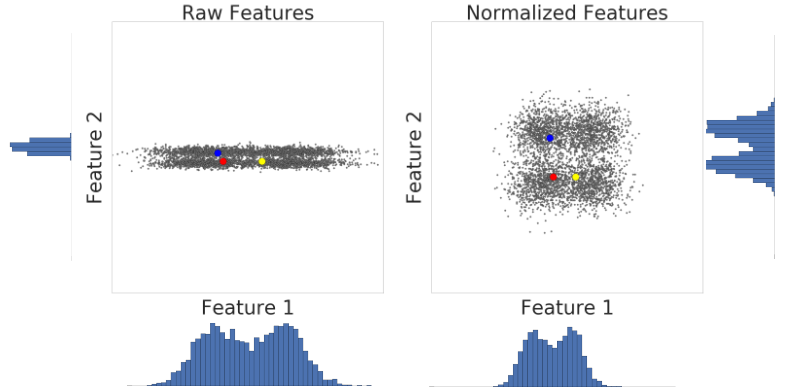
במערך הנתונים הלא מנורמלי בצד ימין, למאפיין 1 ולמאפיין 2, שמוצגים בתרשים על ציר x וציר y בהתאמה, אין את אותו קנה מידה. בצד ימין, הדוגמה האדומה נראית קרובה יותר או דומה יותר לכחול מאשר לצהוב. בצד שמאל, אחרי שינוי הסולם לפי ציון z, לתכונה 1 ולתכונה 2 יש את אותו סולם, והדוגמה האדומה נראית קרובה יותר לדוגמה הצהובה. מערך הנתונים המנורמלי מספק מדד מדויק יותר של הדמיון בין הנקודות.
טרנספורמציות של יומנים
כשמערך נתונים תואם באופן מושלם לחלוקה של חוק העוצמה, שבה הנתונים מקובצים בצורה משמעותית בערכים הנמוכים ביותר, צריך להשתמש בטרנספורמציה לוגריתמית. במאמר שינוי קנה המידה של יומנים מוסבר איך עושים זאת.
לפניכם תצוגה חזותית של מערך נתונים לפי חוק העוצמה לפני ואחרי טרנספורמציית יומן:
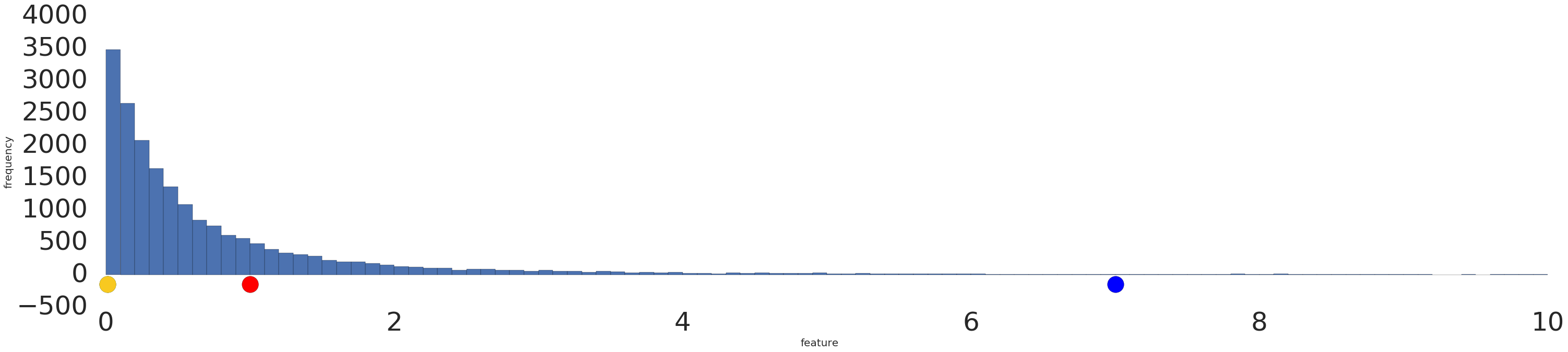
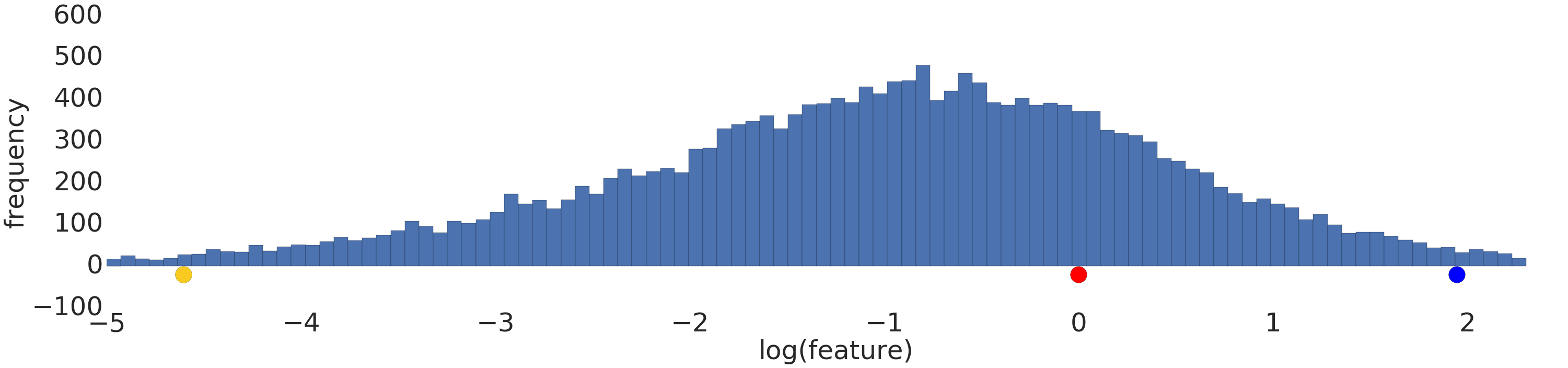
לפני התאמת היומן לעומס (איור 2), הדוגמה האדומה דומה יותר לדוגמה הצהובה. אחרי שינוי הסולם לנתוני יומן (איור 3), הצבע האדום נראה דומה יותר לצבע הכחול.
קוונטילים
חלוקת הנתונים לקונטיינרים לפי רמת ריכוז (quantile) עובדת טוב כשמערך הנתונים לא תואם לחלוקה ידועה. לדוגמה, ניקח את מערך הנתונים הזה:

באופן אינטואיטיבי, שתי דוגמאות דומות יותר אם יש רק כמה דוגמאות ביניהן, ללא קשר לערכים שלהן, והן דומות פחות אם יש הרבה דוגמאות ביניהן. בתצוגה החזותית שלמעלה קשה לראות את המספר הכולל של הדוגמאות שנמצאות בין האדום לצהוב או בין האדום לכחול.
כדי להבין את הדמיון הזה, אפשר לחלק את מערך הנתונים לקוטיליים, או מרווחים שכל אחד מהם מכיל מספר שווה של דוגמאות, ולהקצות את מדד הקוטיל לכל דוגמה. במאמר חלוקה לקטגוריות לפי פלחים (quantile) מוסבר איך עושים את זה.
זוהי ההתפלגות הקודמת שמחולקת לקונטיליים, ומראה שהצבע האדום נמצא קונטיל אחד מהצהוב ושלושה קונטילים מהכחול:
![תרשים שבו מוצגים הנתונים אחרי שהם הוסבו לקונטיליות. הקו מייצג 20 מרווחים.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=19&hl=he)
אפשר לבחור כל מספר \(n\) של פלחים. עם זאת, כדי שהקוינטלים ייצגו בצורה משמעותית את הנתונים הבסיסיים, מערך הנתונים צריך לכלול לפחות\(10n\) דוגמאות. אם אין מספיק נתונים, אפשר לבצע נורמליזציה במקום זאת.
בדיקת ההבנה
בשאלות הבאות, נניח שיש לכם מספיק נתונים כדי ליצור קוינטלים.
שאלה אחת
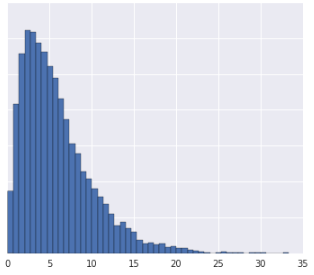
- התפלגות הנתונים היא נורמלית.
- יש לכם תובנות לגבי מה שהנתונים מייצגים בעולם האמיתי, שמצביעות על כך שאין צורך לבצע טרנספורמציה לא לינארית של הנתונים.
שאלה שנייה
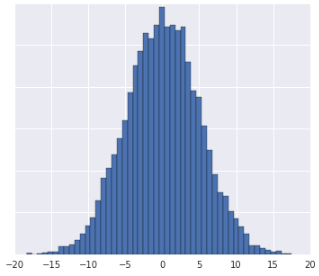
נתונים חסרים
אם במערך הנתונים יש דוגמאות עם ערכים חסרים של מאפיין מסוים, אבל הדוגמאות האלה מופיעות לעיתים רחוקות, אפשר להסיר את הדוגמאות האלה. אם הדוגמאות האלה מופיעות לעיתים קרובות, אפשר להסיר את התכונה הזו לגמרי או לחזות את הערכים החסרים באמצעות דוגמאות אחרות באמצעות מודל של למידת מכונה. לדוגמה, אפשר להשלים נתונים מספריים חסרים באמצעות מודל רגרסיה שהוכשר על נתוני מאפיינים קיימים.
