Phần này xem xét các bước chuẩn bị dữ liệu phù hợp nhất với việc phân cụm trong mô-đun Làm việc với dữ liệu số của khoá học Máy học cấp tốc.
Trong quá trình tạo cụm, bạn tính toán mức độ tương đồng giữa hai ví dụ bằng cách kết hợp tất cả dữ liệu đặc điểm của các ví dụ đó thành một giá trị số. Điều này đòi hỏi các đặc điểm phải có cùng một tỷ lệ, điều này có thể được thực hiện bằng cách chuẩn hoá, chuyển đổi hoặc tạo các phân vị. Nếu muốn biến đổi dữ liệu mà không kiểm tra phân phối của dữ liệu, bạn có thể sử dụng các phân vị theo mặc định.
Điều chỉnh chuẩn dữ liệu
Bạn có thể chuyển đổi dữ liệu cho nhiều đặc điểm theo cùng một tỷ lệ bằng cách chuẩn hoá dữ liệu.
Điểm Z
Bất cứ khi nào bạn thấy một tập dữ liệu có hình dạng gần giống với phân phối Gaussian, bạn nên tính toán điểm z cho dữ liệu đó. Điểm Z là số độ lệch chuẩn của một giá trị so với giá trị trung bình. Bạn cũng có thể sử dụng điểm z khi tập dữ liệu không đủ lớn để tính toán các phân vị.
Hãy xem phần Điều chỉnh theo điểm Z để xem lại các bước.
Dưới đây là hình ảnh trực quan về hai đặc điểm của một tập dữ liệu trước và sau khi điều chỉnh theo tỷ lệ điểm z:
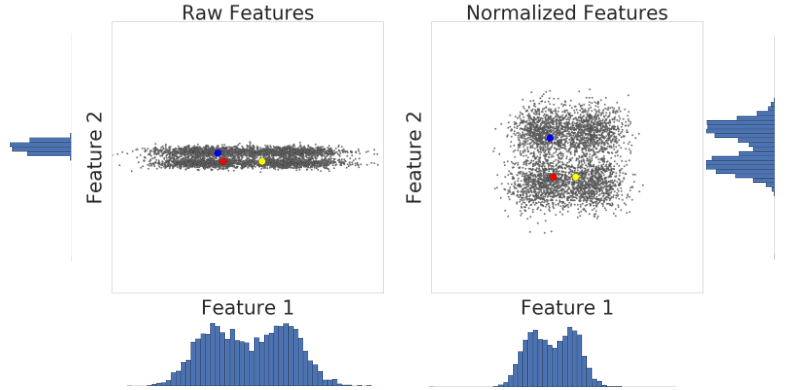
Trong tập dữ liệu chưa chuẩn hoá ở bên trái, Tính năng 1 và Tính năng 2, được biểu đồ tương ứng trên trục x và trục y, không có cùng tỷ lệ. Ở bên trái, ví dụ về màu đỏ có vẻ gần giống với màu xanh dương hơn là màu vàng. Ở bên phải, sau khi điều chỉnh theo tỷ lệ điểm z, Tính năng 1 và Tính năng 2 có cùng tỷ lệ và ví dụ màu đỏ có vẻ gần với ví dụ màu vàng hơn. Tập dữ liệu đã chuẩn hoá cung cấp một phép đo chính xác hơn về mức độ tương đồng giữa các điểm.
Biến đổi nhật ký
Khi một tập dữ liệu tuân thủ hoàn toàn một phân phối quy luật lũy thừa, trong đó dữ liệu tập trung nhiều ở các giá trị thấp nhất, hãy sử dụng phép biến đổi logarit. Hãy xem phần Điều chỉnh theo tỷ lệ nhật ký để xem lại các bước.
Dưới đây là hình ảnh trực quan của một tập dữ liệu theo luật lũy thừa trước và sau khi biến đổi logarit:
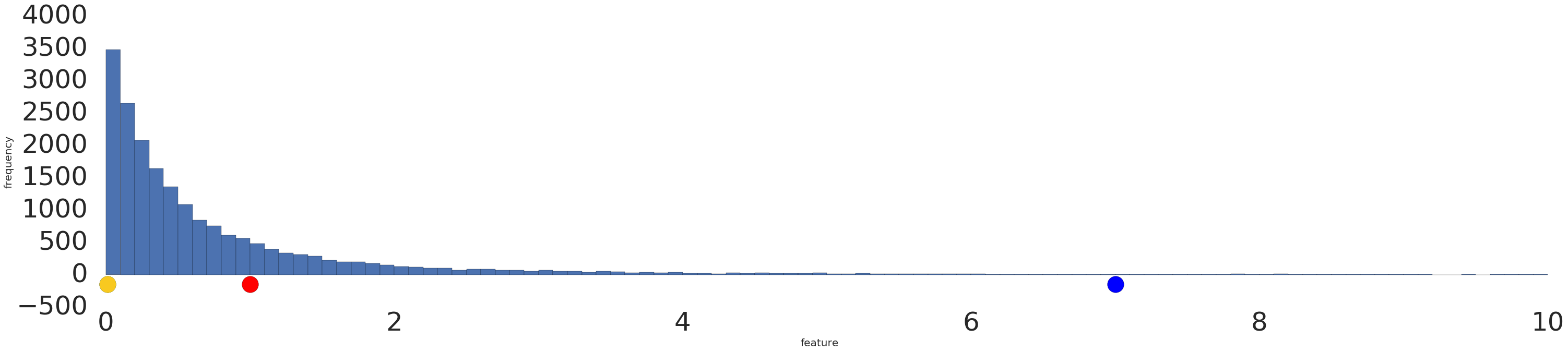
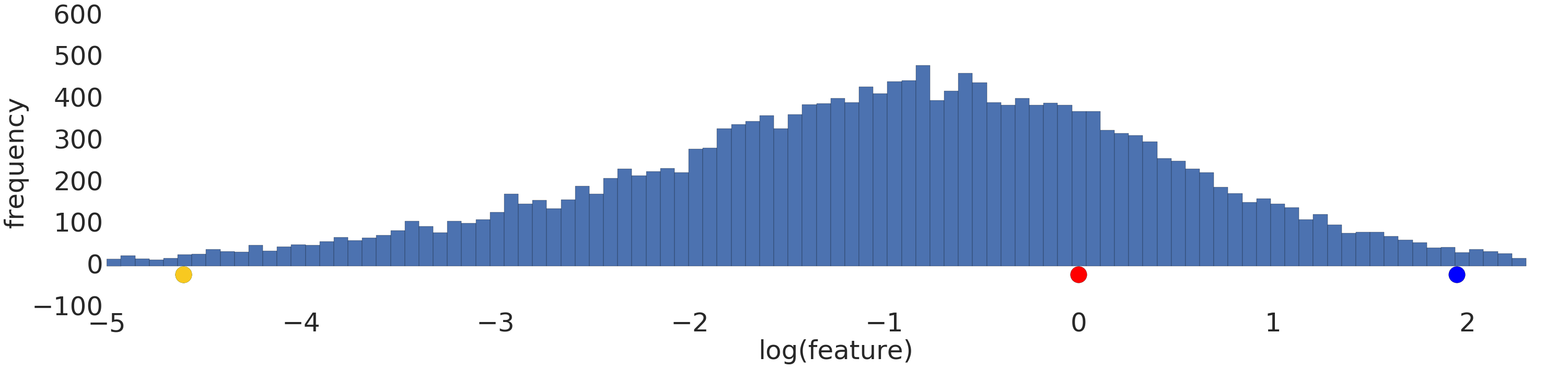
Trước khi điều chỉnh theo tỷ lệ nhật ký (Hình 2), ví dụ màu đỏ có vẻ giống với màu vàng hơn. Sau khi điều chỉnh theo tỷ lệ logarit (Hình 3), màu đỏ trông giống màu xanh dương hơn.
Phân vị
Việc phân chia dữ liệu thành các phân vị sẽ hoạt động hiệu quả khi tập dữ liệu không tuân theo một phân phối đã biết. Ví dụ: hãy lấy tập dữ liệu này:

Theo trực giác, hai ví dụ sẽ giống nhau hơn nếu chỉ có một vài ví dụ nằm giữa hai ví dụ đó, bất kể giá trị của các ví dụ đó, và sẽ khác nhau hơn nếu có nhiều ví dụ nằm giữa hai ví dụ đó. Hình ảnh trực quan ở trên khiến bạn khó thấy tổng số ví dụ nằm giữa màu đỏ và màu vàng hoặc giữa màu đỏ và màu xanh dương.
Bạn có thể hiểu được mức độ tương đồng này bằng cách chia tập dữ liệu thành các tứ phân vị hoặc các khoảng chứa số lượng ví dụ bằng nhau và gán chỉ mục tứ phân vị cho từng ví dụ. Hãy xem phần Nhóm theo tứ phân vị để xem lại các bước.
Dưới đây là bản phân phối trước đó được chia thành các phân vị, cho thấy màu đỏ cách màu vàng một phân vị và cách màu xanh dương ba phân vị:
![Biểu đồ cho thấy dữ liệu sau khi chuyển đổi thành các phân vị. Đường kẻ này đại diện cho 20 khoảng thời gian.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=19&hl=vi)
Bạn có thể chọn số lượng tứ phân vị \(n\) bất kỳ. Tuy nhiên, để các phân vị đại diện một cách có ý nghĩa cho dữ liệu cơ bản, tập dữ liệu của bạn phải có ít nhất\(10n\) ví dụ. Nếu không có đủ dữ liệu, hãy chuẩn hoá.
Kiểm tra mức độ hiểu biết
Đối với các câu hỏi sau, giả sử bạn có đủ dữ liệu để tạo các phân vị.
Câu hỏi 1
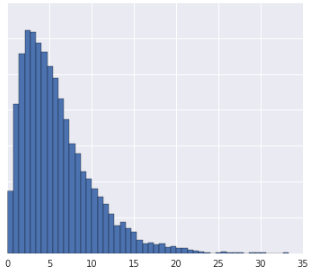
- Phân phối dữ liệu là Gaussian.
- Bạn có một số thông tin chi tiết về nội dung dữ liệu thể hiện trong thực tế, điều này cho thấy dữ liệu không được biến đổi theo phương thức phi tuyến tính.
Câu hỏi 2
Thiếu dữ liệu
Nếu tập dữ liệu của bạn có các ví dụ bị thiếu giá trị cho một tính năng nhất định, nhưng các ví dụ đó hiếm khi xảy ra, thì bạn có thể xoá các ví dụ này. Nếu các ví dụ đó xuất hiện thường xuyên, bạn có thể xoá hoàn toàn tính năng đó hoặc dự đoán các giá trị bị thiếu từ các ví dụ khác bằng cách sử dụng mô hình học máy. Ví dụ: bạn có thể gán dữ liệu số bị thiếu bằng cách sử dụng mô hình hồi quy được huấn luyện dựa trên dữ liệu đặc điểm hiện có.
