ส่วนนี้จะอธิบายขั้นตอนการจัดเตรียมข้อมูลที่เกี่ยวข้องกับการจัดกลุ่มมากที่สุดจากข้อบังคับของการทํางานกับข้อมูลตัวเลขในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ในการจัดกลุ่ม คุณคำนวณความคล้ายคลึงกันระหว่างตัวอย่าง 2 รายการโดยรวมข้อมูลฟีเจอร์ทั้งหมดของตัวอย่างเหล่านั้นเป็นค่าตัวเลข ซึ่งจําเป็นต้องให้ฟีเจอร์มีรูปแบบเดียวกัน ซึ่งทำได้โดยการทำให้เป็นมาตรฐาน การเปลี่ยนรูปแบบ หรือการสร้างควอร์ไทล์ หากต้องการเปลี่ยนรูปแบบข้อมูลโดยไม่ตรวจสอบการแจกแจง ให้ใช้ควอร์ไทล์เป็นค่าเริ่มต้น
การทำให้ข้อมูลเป็นมาตรฐาน
คุณสามารถเปลี่ยนรูปแบบข้อมูลขององค์ประกอบหลายรายการให้เป็นรูปแบบเดียวกันได้โดยการทำให้ข้อมูลเป็นมาตรฐาน
ค่า z
เมื่อเห็นชุดข้อมูลที่มีรูปร่างคล้ายการแจกแจงแบบกaussian คุณควรคํานวณคะแนน z ของข้อมูล ค่า z คือจํานวนค่าเบี่ยงเบนมาตรฐานของค่าหนึ่งๆ จากค่าเฉลี่ย นอกจากนี้ คุณยังใช้คะแนน z ได้เมื่อชุดข้อมูลมีขนาดเล็กเกินไปสําหรับควอร์ไทล์
ดูขั้นตอนต่างๆ ได้ที่หัวข้อการปรับขนาดคะแนน z
ภาพต่อไปนี้แสดงฟีเจอร์ 2 รายการของชุดข้อมูลก่อนและหลังการปรับขนาดคะแนน z
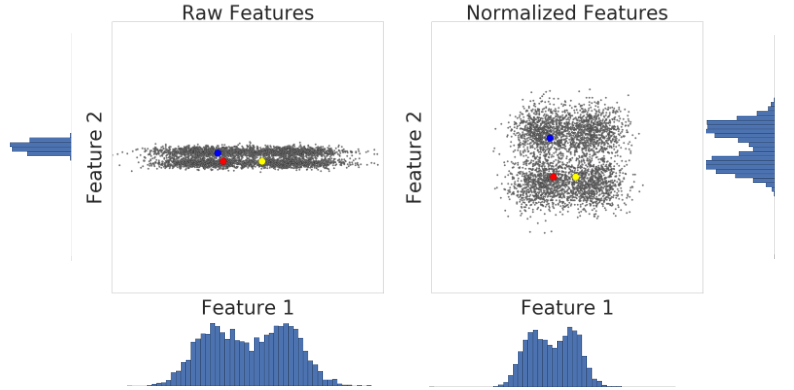
ในชุดข้อมูลที่ไม่มีการแปลงค่าให้เป็นมาตรฐานทางด้านซ้าย ฟีเจอร์ 1 และฟีเจอร์ 2 ที่แสดงเป็นกราฟบนแกน x และ y ตามลำดับไม่มีมาตราส่วนเดียวกัน ตัวอย่างสีแดงทางด้านซ้ายดูใกล้เคียงหรือคล้ายกับสีน้ำเงินมากกว่าสีเหลือง ทางด้านขวา หลังจากการปรับขนาดคะแนน z ฟีเจอร์ที่ 1 และ 2 จะมีมาตราส่วนเดียวกัน และตัวอย่างสีแดงจะปรากฏใกล้กับตัวอย่างสีเหลืองมากขึ้น ชุดข้อมูลที่แปลงเป็นมาตรฐานจะให้การวัดความคล้ายคลึงระหว่างจุดที่แม่นยำยิ่งขึ้น
การเปลี่ยนรูปแบบบันทึก
เมื่อชุดข้อมูลสอดคล้องกับการแจกแจงกฎกำลังอย่างสมบูรณ์แบบ ซึ่งข้อมูลกระจุกตัวอยู่ที่ค่าต่ำสุด ให้ใช้การเปลี่ยนรูปแบบข้อมูลเป็นลอจิก ดูขั้นตอนต่างๆ ได้ที่หัวข้อการปรับขนาดบันทึก
ต่อไปนี้คือการแสดงภาพชุดข้อมูลกฎกำลังก่อนและหลังการเปลี่ยนรูปแบบข้อมูลที่เป็นลอจิก
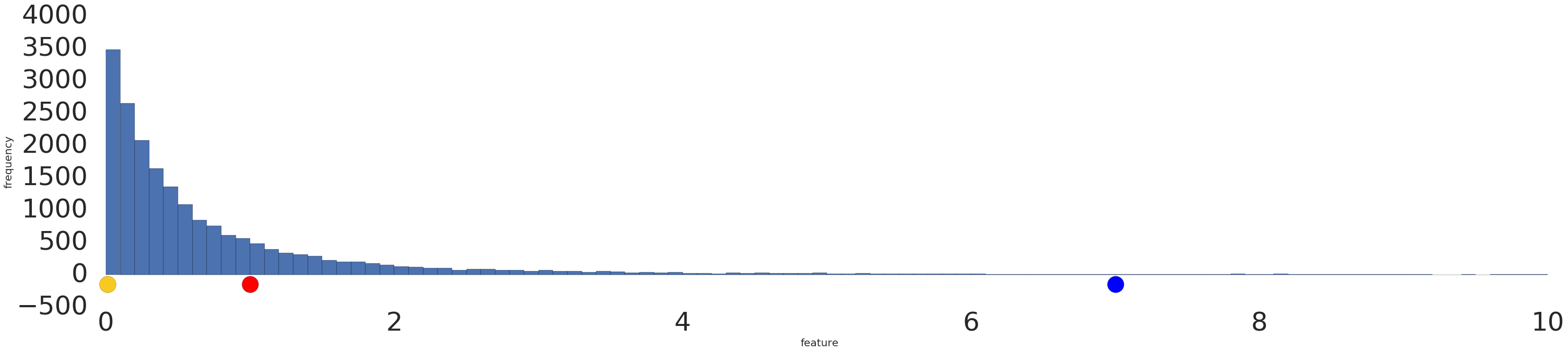
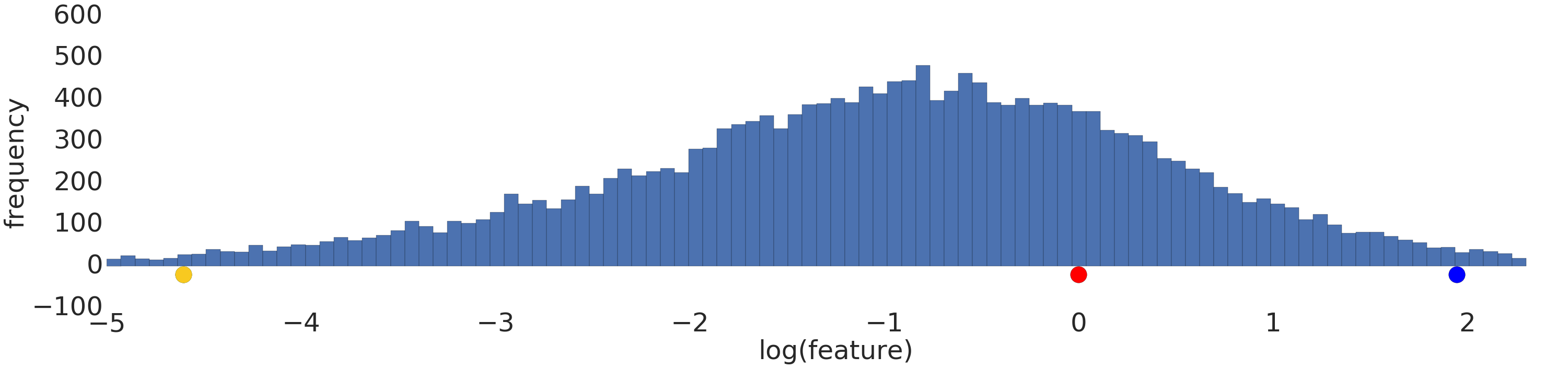
ก่อนการปรับขนาดบันทึก (รูปที่ 2) ตัวอย่างสีแดงจะดูคล้ายกับสีเหลืองมากกว่า หลังจากการปรับขนาดแบบลอจิสติก (รูปที่ 3) สีแดงจะดูคล้ายกับสีน้ำเงินมากขึ้น
ควอไทล์
การแบ่งข้อมูลออกเป็นควอร์ไทล์จะทํางานได้ดีเมื่อชุดข้อมูลไม่เป็นไปตามการแจกแจงที่ทราบ มาดูตัวอย่างชุดข้อมูลนี้

ตัวอย่าง 2 รายการจะคล้ายกันมากขึ้นหากมีตัวอย่างเพียงไม่กี่รายการที่อยู่ระหว่างตัวอย่าง 2 รายการนั้น โดยไม่คำนึงถึงค่าของตัวอย่าง และมีความแตกต่างกันมากขึ้นหากมีตัวอย่างจำนวนมากอยู่ระหว่างตัวอย่าง 2 รายการนั้น ภาพด้านบนทำให้เห็นจํานวนตัวอย่างทั้งหมดที่อยู่ระหว่างสีแดงและสีเหลือง หรือระหว่างสีแดงและสีน้ำเงินได้ยาก
ความเข้าใจเกี่ยวกับความคล้ายคลึงนี้สามารถดึงออกมาได้โดยการแบ่งชุดข้อมูลออกเป็นควอร์ไทล์หรือช่วงที่มีตัวอย่างเท่าๆ กันในแต่ละช่วง และกำหนดดัชนีควอร์ไทล์ให้กับแต่ละตัวอย่าง ดูขั้นตอนต่างๆ ได้ที่หัวข้อการแบ่งกลุ่มข้อมูลตามควอร์ไทล์
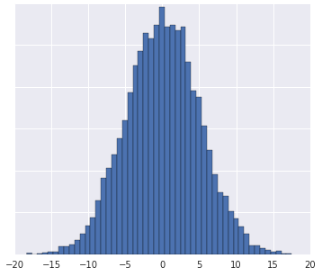
นี่คือการแจกแจงก่อนหน้านี้ที่แบ่งออกเป็นควอร์ไทล์ ซึ่งแสดงให้เห็นว่าสีแดงอยู่ห่างจากสีเหลือง 1 ควอร์ไทล์และอยู่ห่างจากสีน้ำเงิน 3 ควอร์ไทล์
![กราฟแสดงข้อมูลหลังจากแปลงเป็นควอร์ไทล์ เส้นแสดงช่วงเวลา 20 ช่วงเวลา]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=3&hl=th)
คุณเลือกจำนวน \(n\) ควอร์ไทล์ได้ อย่างไรก็ตาม ชุดข้อมูลควรมีตัวอย่างอย่างน้อย\(10n\) รายการเพื่อให้ควอร์ไทล์แสดงข้อมูลพื้นฐานอย่างมีความหมาย หากมีข้อมูลไม่เพียงพอ ให้ใช้การแปลงค่าให้เป็นมาตรฐานแทน
ทดสอบความเข้าใจ
สําหรับคําถามต่อไปนี้ ให้สมมติว่าคุณมีข้อมูลเพียงพอที่จะสร้างควอร์ไทล์
คำถามที่ 1
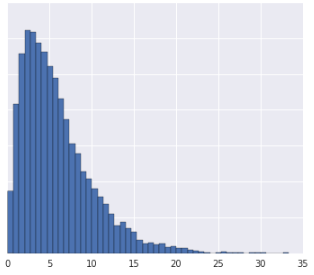
- การแจกแจงข้อมูลเป็นแบบกaussian
- คุณมีข้อมูลเชิงลึกบางอย่างเกี่ยวกับสิ่งที่ข้อมูลแสดงถึงในชีวิตจริง ซึ่งแนะนําว่าไม่ควรเปลี่ยนรูปแบบข้อมูลแบบไม่เป็นเชิงเส้น
คำถามที่ 2
ข้อมูลขาดหาย
หากชุดข้อมูลมีตัวอย่างที่ไม่มีค่าสำหรับฟีเจอร์หนึ่งๆ แต่ตัวอย่างเหล่านั้นเกิดขึ้นไม่บ่อยนัก คุณสามารถนำตัวอย่างเหล่านี้ออกได้ หากตัวอย่างเหล่านั้นเกิดขึ้นบ่อย คุณสามารถนําฟีเจอร์นั้นออกทั้งหมด หรือจะคาดการณ์ค่าที่ขาดหายไปจากตัวอย่างอื่นๆ โดยใช้โมเดลแมชชีนเลิร์นนิงก็ได้ เช่น คุณสามารถประมาณค่าข้อมูลตัวเลขที่ขาดหายไปได้โดยใช้รูปแบบการถดถอยที่ผ่านการฝึกกับข้อมูลฟีเจอร์ที่มีอยู่