In diesem Abschnitt werden die für das Clustern wichtigsten Schritte zur Datenvorbereitung aus dem Modul Mit numerischen Daten arbeiten im Crashkurs zu maschinellem Lernen noch einmal erläutert.
Beim Clustern berechnen Sie die Ähnlichkeit zwischen zwei Beispielen, indem Sie alle Feature-Daten für diese Beispiele in einem numerischen Wert kombinieren. Dazu müssen die Merkmale dieselbe Skala haben. Dies kann durch Normalisieren, Transformieren oder Erstellen von Quantilen erreicht werden. Wenn Sie Ihre Daten transformieren möchten, ohne die Verteilung zu prüfen, können Sie als Standardquantile verwenden.
Daten normalisieren
Sie können Daten für mehrere Features auf dieselbe Skala transformieren, indem Sie sie normalisieren.
Z-Werte
Wenn Sie einen Datensatz sehen, der grob der Form einer Gaußverteilung entspricht, sollten Sie Z-Werte für die Daten berechnen. Z-Werte geben an, wie viele Standardabweichungen ein Wert vom Mittelwert entfernt ist. Sie können Z-Werte auch verwenden, wenn der Datensatz nicht groß genug für Quantile ist.
Eine detaillierte Anleitung finden Sie unter Z-Score-Skalierung.
Hier sehen Sie eine Visualisierung von zwei Merkmalen eines Datensatzes vor und nach der Z-Score-Skalierung:
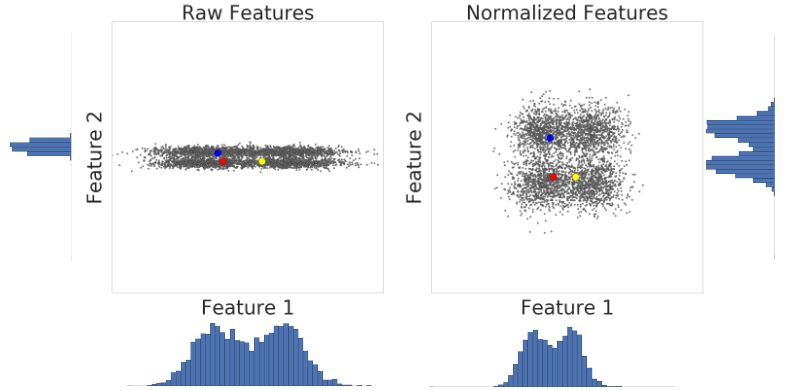
Im nicht normalisierten Datensatz auf der linken Seite haben Feature 1 und Feature 2, die jeweils auf der x- und y-Achse dargestellt sind, nicht dieselbe Skala. Auf der linken Seite ist das rote Beispiel näher oder ähnlicher an Blau als an Gelb. Rechts, nach der Z-Wert-Skalierung, haben Merkmal 1 und Merkmal 2 dieselbe Skala und das rote Beispiel erscheint näher am gelben Beispiel. Der normalisierte Datensatz liefert ein genaueres Maß für die Ähnlichkeit zwischen Punkten.
Logtransformationen
Wenn ein Datensatz genau einem Potenzgesetz entspricht, bei dem sich die Daten stark bei den niedrigsten Werten konzentrieren, verwenden Sie eine Logarithmustransformation. Eine Anleitung dazu finden Sie unter Protokolle skalieren.
Hier sehen Sie eine Visualisierung eines Potenzgesetz-Datasets vor und nach einer Logarithmustransformation:
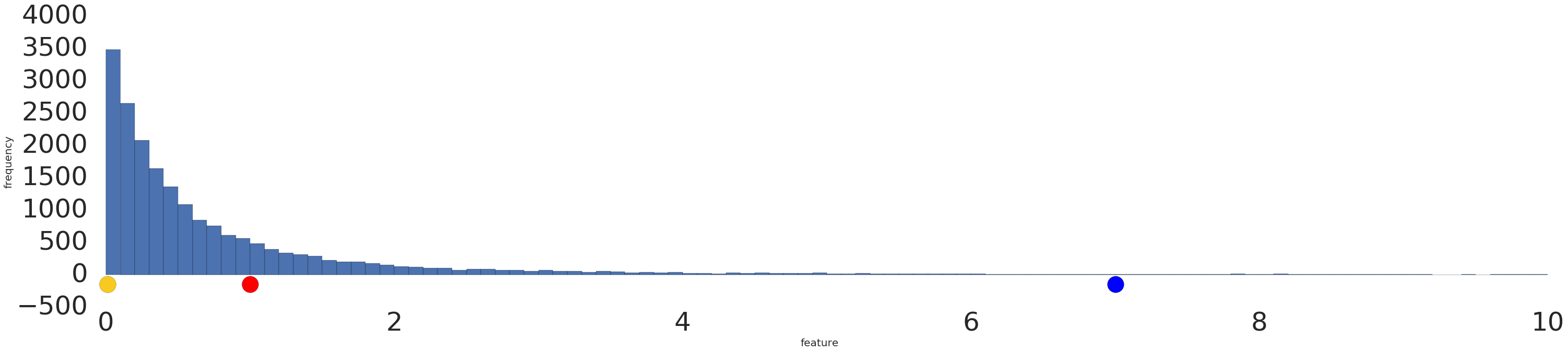
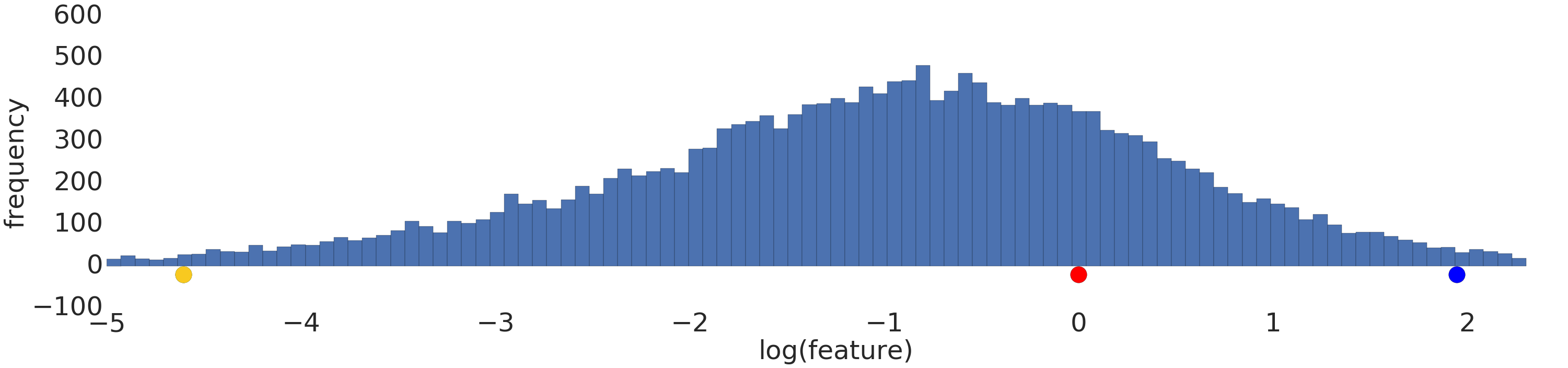
Vor der Logarithmus-Skalierung (Abbildung 2) sieht das rote Beispiel eher gelb aus. Nach der Logarithmus-Skalierung (Abbildung 3) ist Rot der Farbe Blau ähnlicher.
Quantile
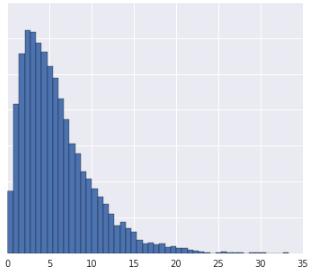
Die Daten in Quantile zu unterteilen, funktioniert gut, wenn der Datensatz nicht einer bekannten Verteilung entspricht. Nehmen wir als Beispiel dieses Dataset:

Intuitiv sind zwei Beispiele ähnlicher, wenn unabhängig von ihren Werten nur wenige Beispiele dazwischen liegen, und weniger ähnlich, wenn viele Beispiele dazwischen liegen. Anhand der obigen Visualisierung ist es schwierig, die Gesamtzahl der Beispiele zu erkennen, die zwischen Rot und Gelb oder zwischen Rot und Blau liegen.
Diese Art der Ähnlichkeit kann hervorgehoben werden, indem der Datensatz in Quantile oder Intervalle unterteilt wird, die jeweils dieselbe Anzahl von Beispielen enthalten, und jedem Beispiel der Quantilenindex zugewiesen wird. Eine detaillierte Anleitung finden Sie unter Quantil-Bucketing.
Hier sehen Sie die vorherige Verteilung in Quantilen. Rot ist ein Quantil von Gelb und drei Quantile von Blau entfernt:
![Ein Diagramm mit den Daten nach der Umwandlung in Quantile. Die Linie steht für 20 Intervalle.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=8&hl=de)
Sie können eine beliebige Anzahl von Quantilen auswählen. \(n\) Damit die Quantile die zugrunde liegenden Daten jedoch sinnvoll repräsentieren, sollte Ihr Datensatz mindestens\(10n\) Beispiele enthalten. Wenn nicht genügend Daten vorhanden sind, normalisieren Sie sie stattdessen.
Wissenstest
Angenommen, Sie haben genügend Daten, um Quantile zu erstellen.
Frage 1
- Die Datenverteilung ist normalverteilt.
- Sie haben einige Informationen dazu, was die Daten in der Realität darstellen, und daraus geht hervor, dass die Daten nicht nichtlinear transformiert werden sollten.
Frage 2
Fehlende Daten
Wenn Ihr Datensatz Beispiele mit fehlenden Werten für ein bestimmtes Feature enthält, diese Beispiele aber selten vorkommen, können Sie sie entfernen. Wenn diese Beispiele häufig vorkommen, können Sie diese Funktion entweder vollständig entfernen oder die fehlenden Werte mithilfe eines Modells für maschinelles Lernen anhand anderer Beispiele vorhersagen. Sie können beispielsweise fehlende numerische Daten imputieren, indem Sie ein Regressionsmodell verwenden, das mit vorhandenen Feature-Daten trainiert wurde.
