W tej sekcji omówimy kroki przygotowania danych, które są najbardziej przydatne do klasteryzacji, z modułu Praca z danymi liczbowymi z Kursu intensywnego z systemów uczących się.
W klasteringu podobieństwo między 2 przypadkami oblicza się, łącząc wszystkie dane cech tych przykładów w wartość liczbową. Wymaga to, aby cechy miały tę samą skalę, co można osiągnąć przez normalizację, transformację lub utworzenie kwantyli. Jeśli chcesz przekształcić dane bez sprawdzania ich rozkładu, możesz użyć kwantyli.
Normalizacja danych
Możesz przekształcić dane dotyczące wielu cech do tej samej skali, normalizując je.
Wyniki znormalizowane
Gdy widzisz zbiór danych o przybliżonym kształcie rozkładu normalnego, musisz obliczyć dla niego wyniki z testu z kryterium z-. Wyniki Z to liczba standardowych odchyleń wartości od średniej. Możesz też używać wartości z-score, gdy zbiór danych jest zbyt mały na zastosowanie kwantyli.
Aby poznać szczegóły, zapoznaj się z artykułem Skalowanie według wartości z-score.
Oto wizualizacja 2 cech zbioru danych przed i po skalowaniu z-score:
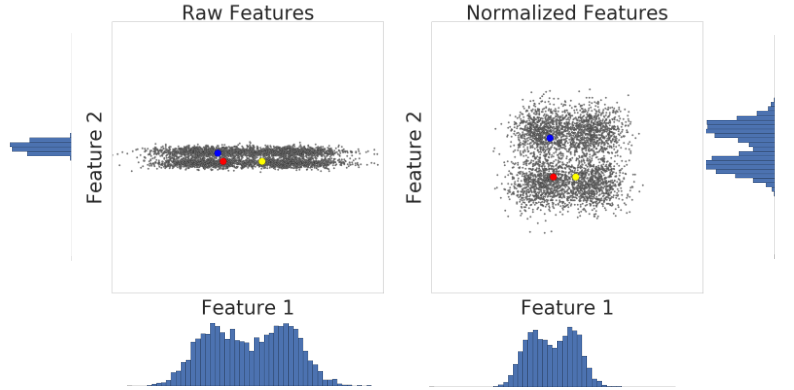
W nieznormalizowanym zbiorze danych po lewej stronie cecha 1 i cecha 2, odpowiednio na osi X i osi Y, nie mają tej samej skali. Po lewej stronie przykład w kolorze czerwonym jest bardziej podobny do niebieskiego niż do żółtego. Po prawej stronie, po zastosowaniu skali z-score, funkcja 1 i 2 mają tę samą skalę, a czerwony przykład jest bliższy przykładowi żółtemu. Znormalizowany zbiór danych zapewnia dokładniejsze pomiary podobieństwa między punktami.
Przekształcenia logarytmiczne
Jeśli zbiór danych idealnie pasuje do rozkładu mocy, w którym dane są mocno skupione w najmniejszych wartościach, użyj transformacji logarytmicznej. Aby poznać kolejne etapy, zapoznaj się z artykułem Logowanie i skalowanie.
Oto wizualizacja zbioru danych o rozkładzie wykładniczym przed i po transformacji logarytmicznej:
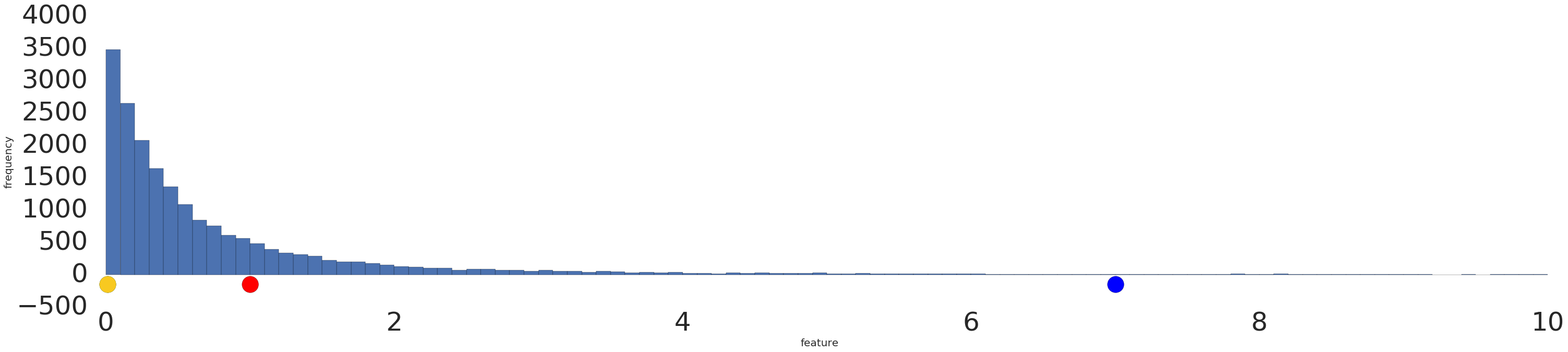
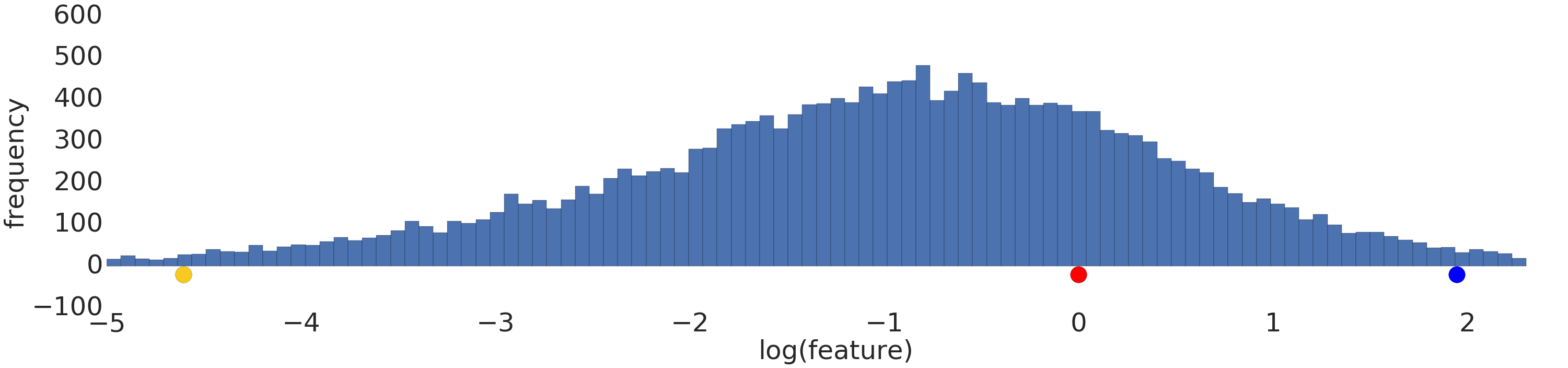
Przed skalowaniem logarytmicznym (rysunek 2) czerwony przykład jest bardziej podobny do żółtego. Po zastosowaniu skalowania logarytmicznego (rysunek 3) kolor czerwony jest bardziej zbliżony do niebieskiego.
Kwantyle
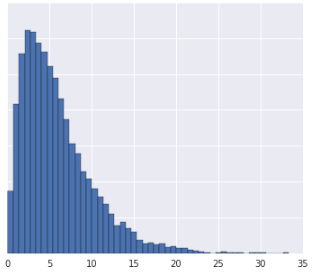
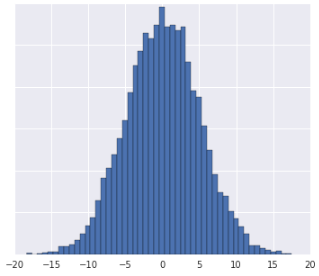
Dzielenie danych na kwantyle sprawdza się, gdy zbiór danych nie jest zgodny z znanym rozkładem. Weźmy na przykład ten zbiór danych:

Intuicyjnie 2 przypadki są bardziej podobne, jeśli między nimi znajduje się tylko kilka przykładów, niezależnie od ich wartości, i bardziej różnią się od siebie, jeśli między nimi znajduje się wiele przykładów. Wizualizacja powyżej utrudnia sprawdzenie łącznej liczby przykładów, które znajdują się między kolorem czerwonym a żółtym lub czerwonym a niebieskim.
Takie zrozumienie podobieństwa można uzyskać, dzieląc zbiór danych na kwantyle, czyli przedziały, z których każdy zawiera taką samą liczbę przykładów, i przypisując każdemu przykładowi indeks kwantyla. Aby poznać szczegóły, zapoznaj się z artykułem Zasoby zbiorcze na podstawie kwantyli.
Oto poprzednia dystrybucja podzielona na kwantyle, pokazująca, że czerwony kolor jest oddalony o 1 kwantyl od żółtego i o 3 kwantyle od niebieskiego:
![Wykres przedstawiający dane po przekształceniu na kwantyle. Linia przedstawia 20 przedziałów.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=8&hl=pl)
Możesz wybrać dowolną liczbę \(n\) kwantyli. Aby jednak kwantyle stanowiły miarodajne odwzorowanie danych źródłowych, zbiór danych powinien zawierać co najmniej\(10n\) przypadków. Jeśli nie masz wystarczającej ilości danych, zamiast tego użyj normalizacji.
Sprawdź swoją wiedzę
W przypadku poniższych pytań przyjmij, że masz wystarczająco dużo danych, aby utworzyć kwantyle.
Pytanie pierwsze
- Rozkład danych jest rozkładem normalnym.
- Masz pewną wiedzę na temat tego, co dane reprezentują w rzeczywistości. Sugeruje to, że nie należy ich przekształcać w sposób nieliniowy.
Pytanie 2
Brakujące dane
Jeśli Twój zbiór danych zawiera przykłady z brakującymi wartościami niektórych cech, ale te przykłady występują rzadko, możesz je usunąć. Jeśli takie przykłady występują często, możesz całkowicie usunąć tę cechę lub przewidzieć brakujące wartości na podstawie innych przykładów za pomocą modelu uczenia maszynowego. Możesz np. uzupełniać brakujące dane liczbowe, używając modelu regresji wytrenowanego na podstawie dotychczasowych danych cech.