En esta sección, se revisan los pasos de preparación de datos más relevantes para el agrupamiento del módulo Cómo trabajar con datos numéricos del Curso intensivo de aprendizaje automático.
En el agrupamiento, se calcula la similitud entre dos ejemplos combinando todos los datos de atributos de esos ejemplos en un valor numérico. Esto requiere que los atributos tengan la misma escala, lo que se puede lograr normalizando, transformando o creando cuantiles. Si deseas transformar tus datos sin inspeccionar su distribución, puedes usar los cuantiles de forma predeterminada.
Normalización de datos
Puedes transformar los datos de varios atributos a la misma escala si los normalizas.
Puntuaciones Z
Cada vez que veas un conjunto de datos con una forma similar a una distribución normal, debes calcular los parámetros z para los datos. Las puntuaciones Z son la cantidad de desviaciones estándar que un valor tiene de la media. También puedes usar las puntuaciones z cuando el conjunto de datos no es lo suficientemente grande para los cuartiles.
Consulta Escalamiento de la puntuación Z para revisar los pasos.
Esta es una visualización de dos atributos de un conjunto de datos antes y después de la escala de puntuación z:
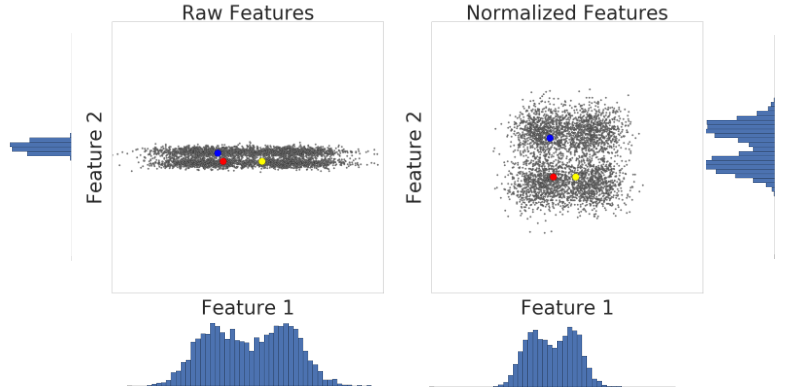
En el conjunto de datos no normalizado de la izquierda, los atributos 1 y 2, que se grafican en los ejes x e y, respectivamente, no tienen la misma escala. A la izquierda, el ejemplo en rojo parece más cercano o más similar al azul que al amarillo. A la derecha, después de la escala de puntuación z, los atributos 1 y 2 tienen la misma escala, y el ejemplo rojo aparece más cerca del ejemplo amarillo. El conjunto de datos normalizado proporciona una medida más precisa de la similitud entre los puntos.
Transformaciones de registro
Cuando un conjunto de datos se ajusta perfectamente a una distribución de ley de potencias, en la que los datos se agrupan mucho en los valores más bajos, usa una transformación logarítmica. Consulta Ajuste de escala de registros para revisar los pasos.
Esta es una visualización de un conjunto de datos de ley de potencia antes y después de una transformación logarítmica:
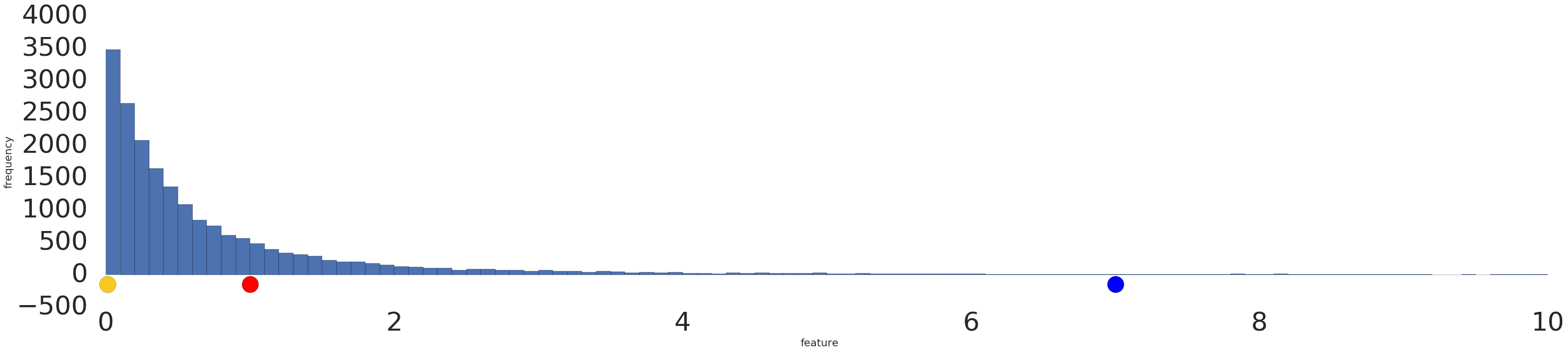
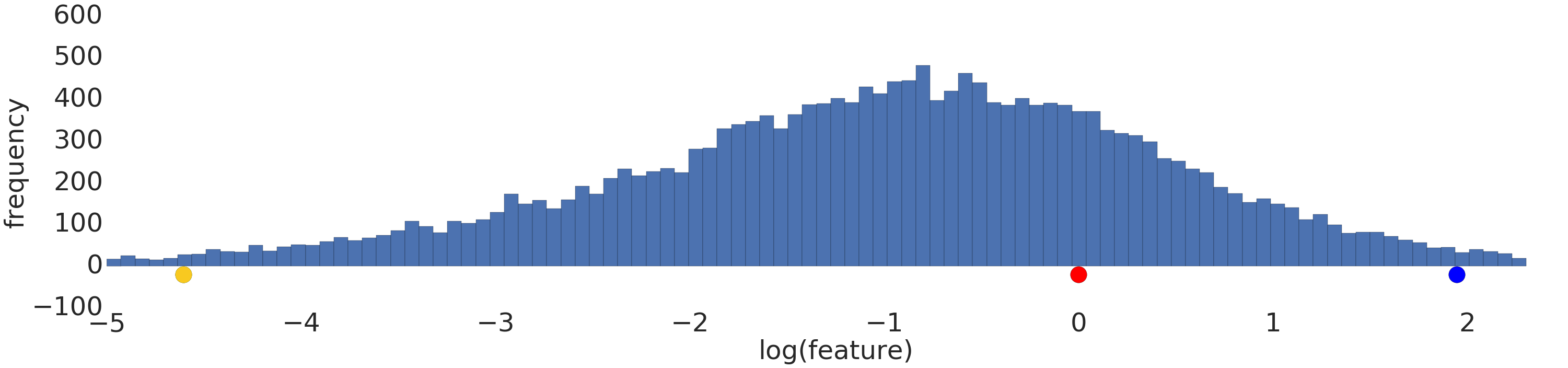
Antes de la escala de registro (Figura 2), el ejemplo en rojo parece más similar al amarillo. Después de la escala de registro (Figura 3), el rojo se ve más similar al azul.
Cuantiles
Agrupar los datos en cuantiles funciona bien cuando el conjunto de datos no cumple con una distribución conocida. Tomemos este conjunto de datos como ejemplo:

De manera intuitiva, dos ejemplos son más similares si solo hay algunos ejemplos entre ellos, independientemente de sus valores, y más disímiles si hay muchos ejemplos entre ellos. La visualización anterior dificulta ver la cantidad total de ejemplos que se encuentran entre el rojo y el amarillo, o entre el rojo y el azul.
Para comprender mejor la similitud, se puede dividir el conjunto de datos en cuantiles, o intervalos que contienen la misma cantidad de ejemplos, y asignar el índice de cuantil a cada ejemplo. Consulta Agrupación en buckets de cuantiles para revisar los pasos.
Esta es la distribución anterior dividida en cuartiles, que muestra que el rojo está a un cuartil de distancia del amarillo y a tres cuartiles de distancia del azul:
![Gráfico que muestra los datos después de la conversión en cuantiles. La línea representa 20 intervalos.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=9&hl=es)
Puedes elegir cualquier cantidad \(n\) de cuantiles. Sin embargo, para que los cuantiles representen de manera significativa los datos subyacentes, tu conjunto de datos debe tener al menos\(10n\) ejemplos. Si no tienes suficientes datos, normaliza los datos.
Verifica tu comprensión
Para las siguientes preguntas, supongamos que tienes suficientes datos para crear cuantiles.
Pregunta uno
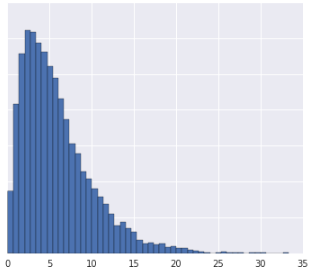
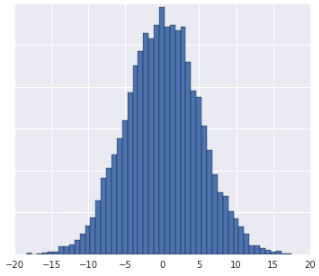
- La distribución de datos es gaussiana.
- Tienes información sobre lo que representan los datos en la realidad, lo que sugiere que no deben transformarse de forma no lineal.
Pregunta dos
Faltan datos
Si tu conjunto de datos tiene ejemplos con valores faltantes para un atributo determinado, pero esos ejemplos ocurren con poca frecuencia, puedes quitarlos. Si esos ejemplos ocurren con frecuencia, puedes quitar esa función por completo, o bien predecir los valores faltantes de otros ejemplos con un modelo de aprendizaje automático. Por ejemplo, puedes imputar datos numéricos faltantes con un modelo de regresión entrenado en datos de atributos existentes.
