均方误差
请参考以下两个图表:
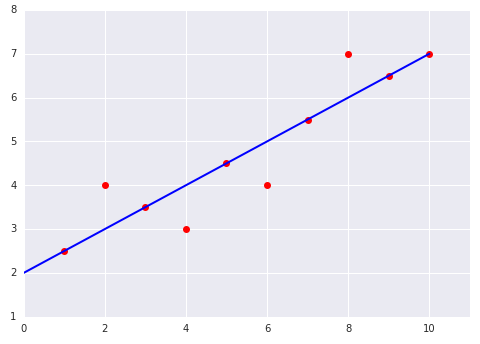 |
<img "units&=ot"" 1="" 2="" <="&otot; above="" alt=", 10 分的曲线图。有一条线穿过 8 个点。165 |
查看以下选项。
以上各个图表中显示的两个数据集的均方误差 (MSE) 较高?
左侧的数据集。
线上的 6 个示例发生的总损失为 0。四个不在线的样本并未远离离线,因此,即便使它们的平方变平方仍会产生较低的值: $$ MSE = \frac{0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 + 0^2 +
0^2} {10} = 0.4$$
右侧的数据集。
线上的 8 个示例导致的总损失为 0。不过,尽管只有两个点在线外,但这两个点离线的距离依然是左图中离群点的 2 倍。平方损失进一步放大这些差异,因此 2 的偏移量产生的损失是 1 的偏移量的四倍。
$$ MSE = \frac{0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2 + 0^2 + 2^2 + 0^2 +
0^2} {10} = 0.8$$
