इस यूनिट में, आपको सबसे आसान और सबसे सामान्य स्प्लिटर एल्गोरिदम के बारे में जानकारी मिलेगी. यह एल्गोरिदम, यहां दी गई सेटिंग में $\mathrm{feature}_i \geq t$ फ़ॉर्म की शर्तें बनाता है:
- बाइनरी क्लासिफ़िकेशन टास्क
- उदाहरणों में वैल्यू मौजूद न होने पर
- उदाहरणों पर पहले से कैलकुलेट किया गया इंडेक्स नहीं है
मान लें कि आपके पास संख्या वाली सुविधा और "नारंगी" और "नीले" रंग के बाइनरी लेबल वाले $n$ उदाहरणों का एक सेट है. डेटासेट $D$ को औपचारिक तौर पर इस तरह से दिखाया जा सकता है:
कहां:
- $x_i$, $\mathbb{R}$ (असल संख्याओं का सेट) में मौजूद संख्या वाली किसी विशेषता की वैल्यू है.
- $y_i$, {orange, blue} में मौजूद बाइनरी क्लासिफ़िकेशन लेबल की वैल्यू है.
हमारा मकसद, थ्रेशोल्ड वैल्यू $t$ (थ्रेशोल्ड) ढूंढना है, ताकि उदाहरणों $D$ को $x_i \geq t$ शर्त के मुताबिक, ग्रुप $T(rue)$ और $F(alse)$ में बांटने से लेबल को अलग करने में मदद मिल सके. उदाहरण के लिए, $T$ में ज़्यादा "नारंगी" उदाहरण और $F$ में ज़्यादा "नीले" उदाहरण.
शैनन एंट्रॉपी, गड़बड़ी का मेज़र होता है. बाइनरी लेबल के लिए:
- उदाहरणों में लेबल संतुलित होने पर (50% नीले और 50% नारंगी), शैनन एन्ट्रोपी सबसे ज़्यादा होती है.
- जब उदाहरणों में मौजूद लेबल पूरी तरह से नीले (100% नीले) या नारंगी (100% नारंगी) रंग के होते हैं, तो शैनन एन्ट्रोपी सबसे कम (वैल्यू शून्य) होती है.

आठवीं इमेज. तीन अलग-अलग एन्ट्रापी लेवल.
हम ऐसी शर्त ढूंढना चाहते हैं जिससे $T$ और $F$ में लेबल डिस्ट्रिब्यूशन के एन्ट्रापी के वेटेंड योग को कम किया जा सके. इससे जुड़ा स्कोर, जानकारी हासिल करना है. यह $D$ के एन्ट्रापी और {$T$,$F$} एन्ट्रापी के बीच का अंतर होता है. इस अंतर को जानकारी हासिल करना कहा जाता है.
नीचे दिए गए चित्र में, खराब स्प्लिट दिखाया गया है. इसमें एन्ट्रापी ज़्यादा है और जानकारी हासिल करने की दर कम है:
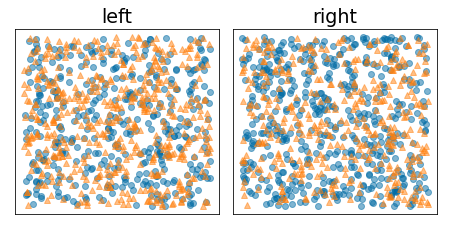
नौवीं इमेज. खराब तरीके से किए गए स्प्लिट से, लेबल का एन्ट्रापी कम नहीं होता.
इसके उलट, नीचे दिए गए आंकड़े में बेहतर स्प्लिट दिखाया गया है, जिसमें एन्ट्रोपी कम हो जाती है (और जानकारी ज़्यादा मिलती है):

10वीं इमेज. सही तरीके से अलग करने से, लेबल का एन्ट्रापी कम हो जाता है.
औपचारिक तौर पर:
\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]
कहां:
- $IG(D,T,F)$, $D$ को $T$ और $F$ में बांटने से मिलने वाली जानकारी है.
- $H(X)$, उदाहरणों के सेट $X$ की एन्ट्रोपी है.
- $|X|$, सेट $X$ में मौजूद एलिमेंट की संख्या है.
- $t$, थ्रेशोल्ड वैल्यू है.
- $pos$, पॉज़िटिव लेबल की वैल्यू है. उदाहरण के लिए, ऊपर दिए गए उदाहरण में "नीला". "पॉज़िटिव लेबल" के तौर पर किसी दूसरे लेबल को चुनने से, एन्ट्रापी या जानकारी हासिल करने की वैल्यू में बदलाव नहीं होता.
- $R(X)$, उदाहरण $X$ में मौजूद पॉज़िटिव लेबल वैल्यू का अनुपात है.
- $D$, डेटासेट है (जैसा कि इस यूनिट में पहले बताया गया है).
नीचे दिए गए उदाहरण में, हम एक संख्या वाली वैल्यू $x$ वाले बाइनरी क्लासिफ़िकेशन डेटासेट पर विचार करते हैं. नीचे दी गई इमेज में, अलग-अलग थ्रेशोल्ड $t$ वैल्यू (x-ऐक्सिस) के लिए दिखाया गया है:
- फ़ीचर $x$ का हिस्टोग्राम.
- थ्रेशोल्ड वैल्यू के हिसाब से, $D$, $T$, और $F$ सेट में "नीले" उदाहरणों का अनुपात.
- $D$, $T$, और $F$ में एन्ट्रॉपी.
- जानकारी हासिल करना; इसका मतलब है कि उदाहरणों की संख्या के हिसाब से, $D$ और {$T$,$F$} के बीच एन्ट्रापी डेल्टा.
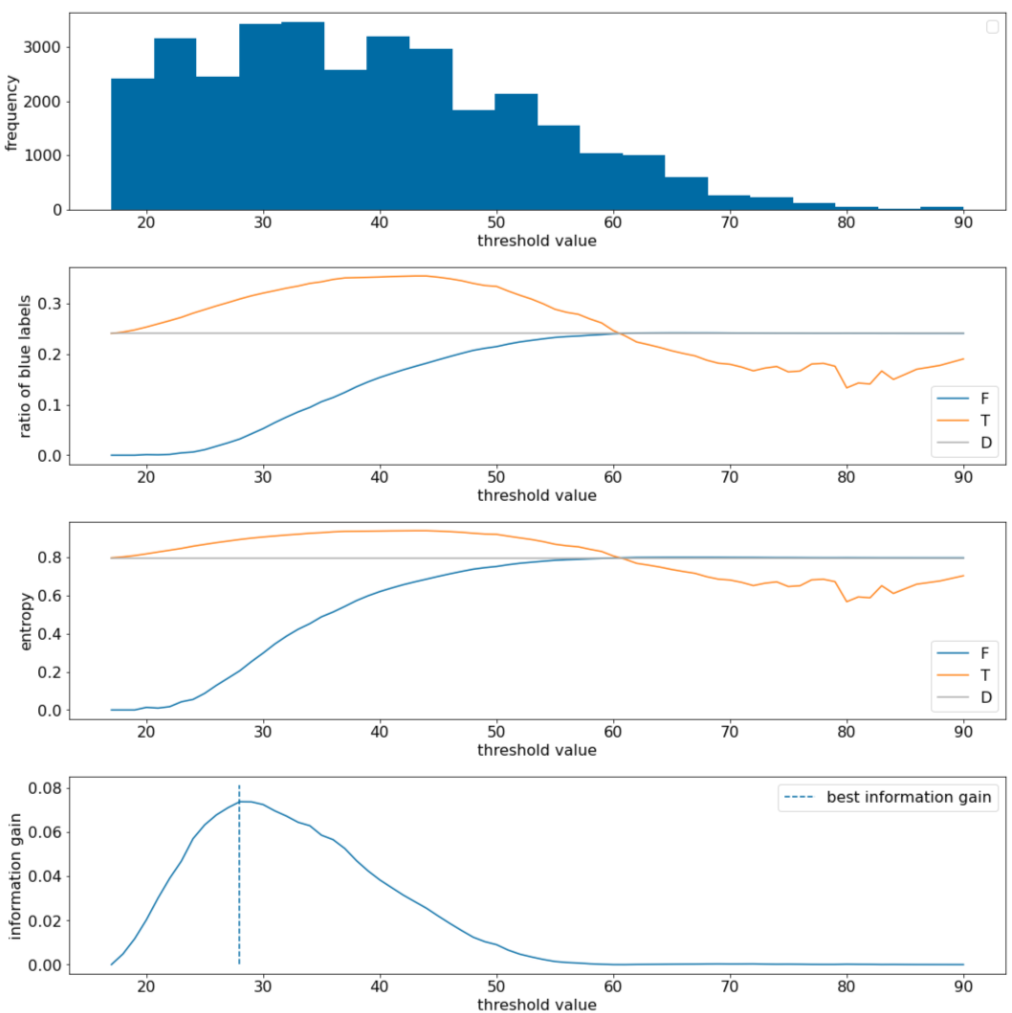
11वां चित्र. चार थ्रेशोल्ड प्लॉट.
इन प्लॉट में ये चीज़ें दिखती हैं:
- "फ़्रीक्वेंसी" प्लॉट से पता चलता है कि 18 से 60 के बीच के डेटा की संख्या ज़्यादा है. वैल्यू के बड़े स्पैड का मतलब है कि संभावित स्प्लिट बहुत ज़्यादा हैं. यह मॉडल को ट्रेन करने के लिए अच्छा है.
डेटासेट में "नीले" लेबल का अनुपात ~25% है. "नीले लेबल का अनुपात" प्लॉट से पता चलता है कि थ्रेशोल्ड वैल्यू 20 से 50 के बीच होने पर:
- $T$ सेट में "नीले" लेबल के उदाहरणों की संख्या ज़्यादा है. थ्रेशोल्ड 35 के लिए, यह संख्या 35% तक हो सकती है.
- $F$ सेट में, "नीले" लेबल के उदाहरणों की संख्या कम है (थ्रेशोल्ड 35 के लिए सिर्फ़ 8%).
"नीले लेबल का अनुपात" और "एन्ट्रापी" प्लॉट, दोनों से पता चलता है कि थ्रेशोल्ड की इस रेंज में, लेबल को एक-दूसरे से अलग किया जा सकता है.
इस नतीजे की पुष्टि, "जानकारी हासिल करना" प्लॉट में की गई है. हमें पता चलता है कि जानकारी हासिल करने की सबसे ज़्यादा वैल्यू, t~=28 पर मिलती है. यह वैल्यू ~0.074 होती है. इसलिए, स्प्लिटर से मिली शर्त यह होगी कि $x \geq 28$.
जानकारी का फ़ायदा हमेशा सकारात्मक या शून्य होता है. थ्रेशोल्ड वैल्यू, अपनी ज़्यादा से ज़्यादा / कम से कम वैल्यू पर पहुंचने के साथ-साथ यह शून्य पर पहुंच जाती है. ऐसे मामलों में, $F$ या $T$ खाली हो जाता है, जबकि दूसरे में पूरा डेटासेट होता है और $D$ में मौजूद एन्ट्रॉपी के बराबर एन्ट्रॉपी दिखाता है. जब $H(T)$ = $H(F)$ = $H(D)$ हो, तो जानकारी का फ़ायदा शून्य भी हो सकता है. थ्रेशोल्ड 60 पर, $T$ और $F$, दोनों के लिए "नीले" लेबल का अनुपात, $D$ के बराबर होता है और जानकारी का फ़ायदा शून्य होता है.
वास्तविक संख्याओं के सेट ($\mathbb{R}$) में, $t$ की संभावित वैल्यू अनंत होती हैं. हालांकि, सीमित उदाहरणों के आधार पर, $D$ को $T$ और $F$ में बांटने के लिए, सीमित विकल्प ही मौजूद होते हैं. इसलिए, जांच के लिए $t$ की सिर्फ़ सीमित वैल्यू का इस्तेमाल किया जा सकता है.
एक क्लासिक तरीका यह है कि वैल्यू xi को बढ़ते क्रम में क्रम से लगाएं xs(i), ताकि:
इसके बाद, $x_i$ की क्रम से लगाई गई वैल्यू के बीच की हर वैल्यू के लिए, $t$ की जांच करें. उदाहरण के लिए, मान लें कि आपके पास किसी खास सुविधा की 1,000 फ़्लोटिंग-पॉइंट वैल्यू हैं. मान लें कि क्रम से लगाने के बाद, पहली दो वैल्यू 8.5 और 8.7 हैं. इस मामले में, जांच करने के लिए पहली थ्रेशोल्ड वैल्यू 8.6 होगी.
आम तौर पर, हम t के लिए इन वैल्यू का इस्तेमाल करते हैं:
इस एल्गोरिदम को लागू करने में लगने वाला समय, $\mathcal{O} ( n \log n) $ होता है. इसमें $n$, नोड में मौजूद उदाहरणों की संख्या होती है. ऐसा, सुविधा की वैल्यू को क्रम से लगाने की वजह से होता है. डिसिज़न ट्री पर लागू होने पर, स्प्लिटर एल्गोरिदम हर नोड और हर सुविधा पर लागू होता है. ध्यान दें कि हर नोड को अपने पैरंट के उदाहरणों में से करीब आधा हिस्सा मिलता है. इसलिए, मास्टर थीओरम के मुताबिक, इस स्प्लिटर की मदद से डिसिज़न ट्री को ट्रेनिंग देने में लगने वाला समय:
कहां:
- $m$, फ़ीचर की संख्या है.
- $n$, ट्रेनिंग के उदाहरणों की संख्या है.
इस एल्गोरिदम में, सुविधाओं की वैल्यू मायने नहीं रखती. सिर्फ़ क्रम मायने रखता है. इस वजह से, यह एल्गोरिदम, सुविधा की वैल्यू के स्केल या डिस्ट्रिब्यूशन के आधार पर काम नहीं करता. इसलिए, हमें डिसीज़न ट्री को ट्रेन करते समय, संख्या वाली सुविधाओं को नॉर्मलाइज़ या स्केल करने की ज़रूरत नहीं होती.