W tej jednostce omawiamy różne typy warunków używanych do tworzenia drzewek decyzyjnych.
Warunki równoległe i ukośne
Warunek wyrównany do osi dotyczy tylko jednej cechy. Warunek pośredni obejmuje wiele cech. Przykładem warunku dopasowanego do osi jest:
num_legs ≥ 2
Poniżej przedstawiono przykład warunku ukośnego:
num_legs ≥ num_fingers
Drzewa decyzyjne są często trenowane tylko z warunkami dopasowanymi do osi. Jednak ukośne podziały są bardziej efektywne, ponieważ mogą wyrażać bardziej złożone wzorce. Rozdzielenie danych na części nierówne może czasami przynieść lepsze wyniki, ale kosztem wyższych kosztów trenowania i wyciągania wniosków.
split_axis="SPARSE_OBLIQUE".
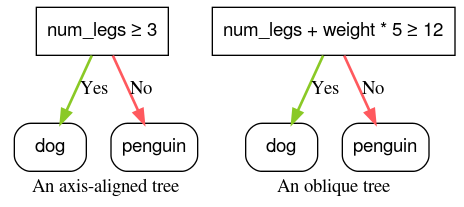
Ilustracja 4. Przykłady warunku dopasowanego do osi i warunku ukośnego.
Wyznaczenie na wykresie tych 2 warunków daje następującą separację przestrzeni cech:
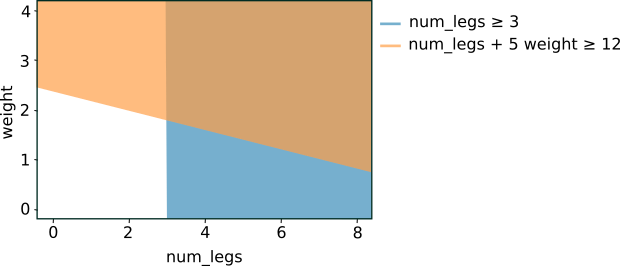
Rysunek 5. Rozdzielenie przestrzeni cech dla warunków przedstawionych na rysunku 4.
Warunki binarne a niebinarne
Warunki z 2 możliwymi wynikami (np. prawda lub fałsz) nazywamy warunkami binarnymi. Drzewa decyzyjne zawierające tylko warunki binarne nazywane są drzewami decyzyjnymi binarnymi.
Warunki niebinarne mają więcej niż 2 możliwe wyniki. Dlatego warunki niebinarne mają większą moc dyskryminacyjną niż warunki binarne. Decyzje zawierające co najmniej 1 warunek niebinarny nazywamy niebinarnymi drzewami decyzji.
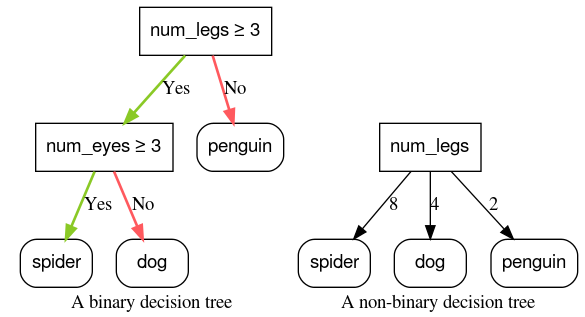
Ilustracja 6. Drzewa decyzyjne binarne i niebinarne.
Warunki z zbyt dużą mocą również sprzyjają nadmiernemu dopasowaniu. Z tego powodu lasy decyzyjne zazwyczaj używają binarnych drzew decyzyjnych, więc w tym kursie skupimy się na nich.
Najczęstszym typem warunku jest warunek progowy wyrażony w postaci:
feature ≥ threshold
Na przykład:
num_legs ≥ 2
Istnieją też inne typy warunków. Oto inne często używane typy warunków binarnych:
Tabela 2. Typowe typy warunków binarnych.
| Nazwa | Warunek | Przykład |
| warunek progowy | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| warunek równości | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| warunek w zestawie | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| warunek ukośny | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | 5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| brakuje funkcji | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |