Esta unidad se enfoca en los diferentes tipos de condiciones que se usan para crear árboles de decisión.
Condiciones oblicuas en comparación con las alineadas con el eje
Una condición alineada con el eje solo incluye una sola función. Una condición oblicua implica varias características. Por ejemplo, la siguiente es una condición alineada con el eje:
num_legs ≥ 2
Mientras que la siguiente es una condición oblicua:
num_legs ≥ num_fingers
A menudo, los árboles de decisión se entrenan solo con condiciones alineadas con el eje. Sin embargo, las divisiones oblicuas son más potentes porque pueden expresar patrones más complejos. En ocasiones, las divisiones oblicuas producen mejores resultados a costa de costos de inferencia y entrenamiento más altos.
split_axis="SPARSE_OBLIQUE".
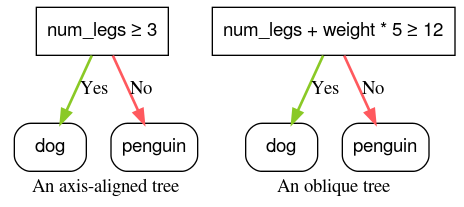
Figura 4: Ejemplos de una condición alineada con el eje y una oblicua.
Si se grafican las dos condiciones anteriores, se obtiene la siguiente separación del espacio de características:
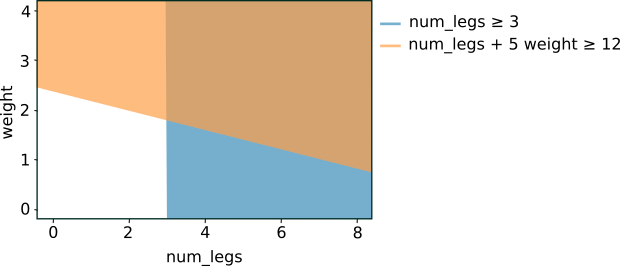
Figura 5: Separación del espacio de características para las condiciones de la Figura 4.
Condiciones binarias y no binarias
Las condiciones con dos resultados posibles (por ejemplo, verdadero o falso) se denominan condiciones binarias. Los árboles de decisión que solo contienen condiciones binarias se llaman árboles de decisión binarios.
Las condiciones no binarias tienen más de dos resultados posibles. Por lo tanto, las condiciones no binarias tienen más poder discriminativo que las condiciones binarias. Las decisiones que contienen una o más condiciones no binarias se denominan árboles de decisión no binarios.
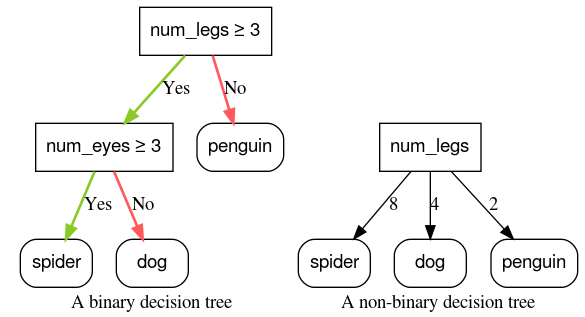
Figura 6: Árboles de decisión binarios y no binarios.
Las condiciones con demasiada potencia también tienen más probabilidades de sobreajustar. Por este motivo, los bosques de decisión generalmente usan árboles de decisión binarios, por lo que este curso se enfocará en ellos.
El tipo de condición más común es la condición de umbral, que se expresa de la siguiente manera:
feature ≥ threshold
Por ejemplo:
num_legs ≥ 2
Existen otros tipos de condiciones. A continuación, se muestran otros tipos de condiciones binarias que se usan con frecuencia:
Tabla 2. Tipos comunes de condiciones binarias.
| Nombre | Afección | Ejemplo |
| condición de umbral | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| condición de igualdad | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{especie} = ``gato"$ |
| condición del conjunto | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| condición oblicua | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| falta la función | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |
