隨機樹系
隨機森林 (RF) 是決策樹的集合,其中每個決策樹都會使用特定的隨機雜訊進行訓練。隨機森林是決策樹集成的最常見形式。本單元將討論幾種建立獨立決策樹的技術,以提高建立有效隨機森林的機率。
標記
Bagging (bootstrap aggregating) 是指在訓練集的隨機子集上訓練每個決策樹。換句話說,隨機森林中的每個決策樹都會針對不同的子集訓練。
標記功能很特別,每個決策樹都會針對原始訓練集的數量訓練相同的範例。舉例來說,如果原始訓練集包含 60 個例子,則每個決策樹都會以 60 個例子進行訓練。不過,袋裝法只會在子集 (通常為 67%) 的範例上訓練每個決策樹。因此,在訓練特定決策樹時,子集內的部分 40 個範例必須重複使用。這種重複使用方式稱為「以取代方式訓練」。
舉例來說,表格 6 顯示袋子法如何將六個例子分散到三個決策樹中。請注意以下事項:
- 每個決策樹會訓練總共六個範例。
- 每個決策樹都會針對不同的範例進行訓練。
- 每個決策樹都會重複使用特定範例。舉例來說,在訓練決策樹 1 時,例子 4 會用到兩次,因此在決策樹 1 中,例子 4 的學習權重實際上會加倍。
表 6. 在三個決策樹中標記六個訓練範例。每個數字代表在特定決策樹 (1-3) 的訓練資料集中,重複指定訓練範例 (#1-6) 的次數。
| 訓練範例 | ||||||
|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | |
| 原始資料集 | 1 | 1 | 1 | 1 | 1 | 1 |
| 決策樹 1 | 1 | 1 | 0 | 2 | 1 | 1 |
| 決策樹 2 | 3 | 0 | 1 | 0 | 2 | 0 |
| 決策樹 3 | 0 | 1 | 3 | 1 | 0 | 1 |
在袋化法中,每個決策樹幾乎都會根據原始訓練集的總例數進行訓練。以較多或較少的示例訓練每個決策樹,通常會降低隨機森林的品質。
雖然原始隨機森林論文並未提及,但有時會「不替換」的方式抽樣示例,也就是在決策樹訓練集內,訓練示例不得出現超過一次。舉例來說,在前述表格中,所有值都會是 0 或 1。
bootstrap_training_dataset=False屬性取樣
屬性取樣是指在每個節點上只測試隨機的子集,而不是在所有可用的功能上尋找最佳條件。決策樹的每個節點都會隨機取樣測試功能組合。
下圖的決策樹說明瞭屬性 / 功能取樣。以下是使用 5 個特徵 (f1-f5) 訓練的決策樹。藍色節點代表已測試的功能,白色節點則代表未測試的功能。條件是根據經過最佳測試的功能 (以紅色虛線表示) 建立。
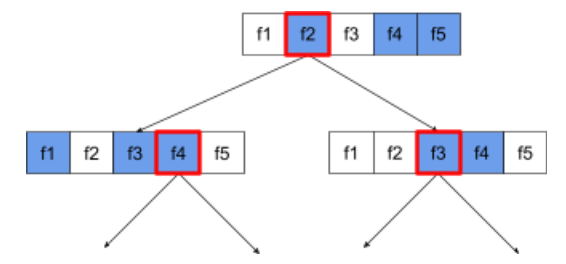
圖 21. 屬性取樣。
屬性取樣比率是重要的正則化超參數。上圖使用了約 ⅗ 的比例。許多隨機森林實作項目會根據預設,針對回歸測試 1/3 的功能,以及針對分類測試 sqrt(功能數量)。
在 TF-DF 中,下列超參數可控制屬性取樣:
num_candidate_attributesnum_candidate_attributes_ratio
舉例來說,如果 num_candidate_attributes_ratio=0.5,則每個節點會測試一半的特徵。
停用決策樹規則化
隨機森林中的個別決策樹會在沒有修剪的情況下進行訓練。(請參閱「過度擬合和去除無關特徵」)。這會產生過於複雜的樹狀結構,導致預測品質不佳。系統會將樹狀圖組合起來,產生更準確的整體預測結果,而非對個別樹狀圖進行規則化。
我們預期隨機森林的訓練和測試準確度會有所不同。隨機森林的訓練準確度通常會高得多 (有時甚至等於 100%)。不過,隨機森林的訓練精確度非常高是「正常」,並非表示隨機森林過度擬合。
兩個隨機來源 (袋裝和屬性取樣) 可確保決策樹之間的相對獨立性。這項獨立性可修正個別決策樹的過度擬合問題。因此,集成模型不會過度擬合。我們會在下一單元說明這種非直覺效果。
Pure 隨機森林訓練程序沒有每個葉節的最大深度或最小觀察次數。在實際操作中,限制每個葉節的最大深度和最小觀察次數會很有幫助。根據預設,許多隨機森林都會使用下列預設值:
- 最大深度約為 16
- 每個葉節的觀察值數量下限約為 5。
您可以調整這些超參數。
雜訊清晰度
為什麼隨機雜訊會改善隨機森林的品質?為了說明隨機雜訊的好處,圖 22 顯示了經過訓練的傳統 (裁剪) 決策樹和隨機森林的預測結果,這些訓練資料是從幾個簡單的橢圓形圖案二維問題示例中取得。
橢圓形圖案很難讓決策樹和決策森林演算法學習軸對齊條件,因此是個很好的範例。請注意,經過裁剪的決策樹無法獲得與隨機森林相同品質的預測結果。
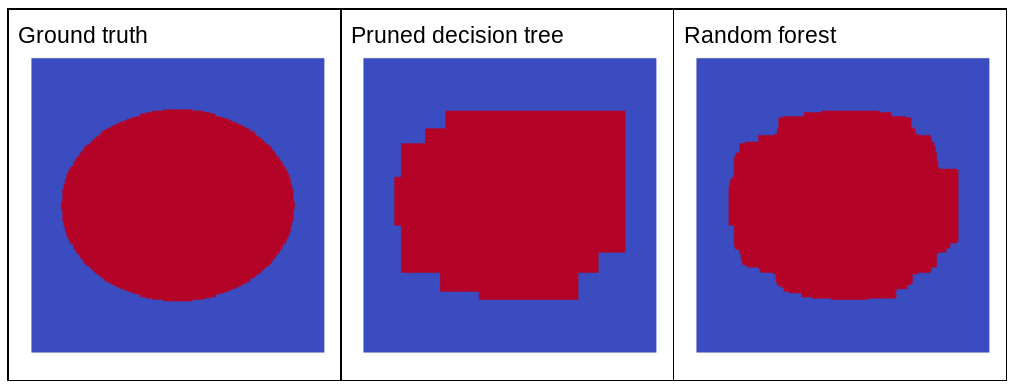
圖 22. 實際資料與單一經過裁剪的決策樹所產生的預測結果,以及隨機森林所產生的預測結果。
下一個圖表顯示隨機森林中前三個未經過修剪的決策樹預測結果,也就是說,決策樹都是使用以下項目的組合進行訓練:
- bagging
- 屬性取樣
- 停用剪枝
請注意,這三個決策樹的個別預測結果,比起上圖中經過修剪的決策樹預測結果,準確度較低。不過,由於個別決策樹的誤差僅有微弱的相關性,因此這三個決策樹會組合成集合,以便做出有效的預測。
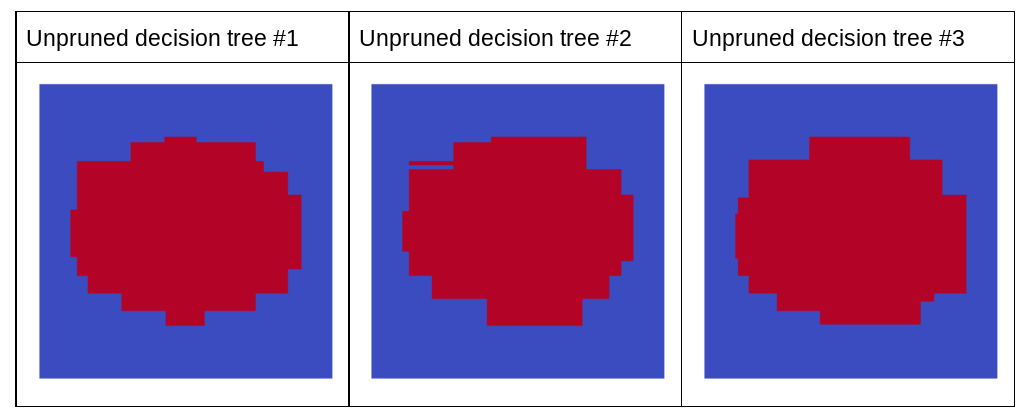
圖 23. 三個未經修剪的決策樹,可建立有效的集成模型。
由於隨機森林的決策樹不會修剪,因此訓練隨機森林不需要驗證資料集。在實際情況中,尤其是在小型資料集的情況下,模型應以所有可用資料進行訓練。
訓練隨機森林時,隨著加入的決策樹增加,錯誤率幾乎總是會降低,也就是說,模型的品質幾乎總是會提升。是的,新增更多決策樹幾乎總是會降低隨機森林的誤差。換句話說,新增更多決策樹不會導致隨機森林過度擬合。在某個時間點,模型就會停止改善。Leo Breiman 曾說過一句名言:「隨機森林不會過度擬合,因為會加入更多樹狀結構」。
舉例來說,下圖顯示隨機森林模型的測試評估結果,以及新增更多決策樹的情況。準確度迅速提升,直到 0.865 左右達到平衡點。不過,加入更多決策樹不會導致準確度降低,也就是說,模型不會過度擬合。這項行為 (大多) 一律為真,且不受超參數影響。
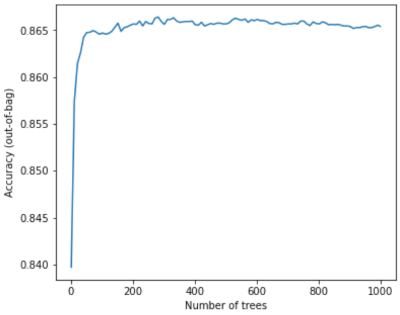
圖 24. 隨著更多決策樹加入隨機森林,準確度會維持不變。