機器學習詞彙表：機器學習基礎知識

本頁面包含機器學習基礎術語。如要查看所有詞彙，請按這裡。

A

精確度

#fundamentals

#指標

正確分類預測次數除以預測總次數。也就是：

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

舉例來說，如果模型做出 40 項正確預測和 10 項錯誤預測，準確率為：

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

二元分類會為正確預測和不正確預測的不同類別提供特定名稱。因此，二元分類的準確度公式如下：

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

其中：

• TP 是真陽性 (正確預測) 的數量。
• TN 是真陰性 (正確預測) 的數量。
• FP 是偽陽性 (不正確預測) 的數量。
• FN 是偽陰性 (不正確預測) 的數量。

比較準確率與精確度和喚回度的異同。

按一下圖示，即可查看準確度和類別不平衡資料集的詳細資料。

雖然準確率在某些情況下是很有價值的指標，但在其他情況下卻可能造成誤導。請注意，準確度通常不適合用來評估處理類別不平衡資料集的分類模型。

舉例來說，假設某個亞熱帶城市每世紀只會下雪 25 天，由於無雪天數 (負類別) 遠多於有雪天數 (正類別)，因此這個城市的降雪資料集屬於不平衡資料集。假設有個二元分類模型每天都會預測是否會下雪，但每天都只預測「不會下雪」。這個模型非常準確，但沒有預測能力。 下表摘要列出百年預測結果：

類別	數字
TP	0
TN	36499
FP	0
FN	25

因此，這個模型的準確度為：

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

雖然 99.93% 的準確率看起來非常驚人，但模型實際上沒有預測能力。

對於在類別不平衡資料集上訓練的模型，精確度和喚回度通常比準確率更有用。

---

詳情請參閱機器學習速成課程中的「分類：準確度、喚回率、精確度和相關指標」。

啟動函式

#fundamentals

這項函式可讓類神經網路學習特徵與標籤之間的非線性 (複雜) 關係。

常見的啟動函式包括：

• ReLU
• Sigmoid

啟動函式的圖形絕不會是單一直線。 舉例來說，ReLU 活化函式的繪圖包含兩條直線：

Sigmoid 啟動函式的繪圖如下所示：

按一下圖示即可查看範例。

在類神經網路中，活化函數會操控神經元所有輸入值的加權總和。如要計算加權總和，神經元會將相關值和權重的乘積加總。舉例來說，假設神經元的相關輸入內容如下：

輸入值	輸入重量
2	-1.3
-1	0.6
3	0.4

因此加權後的總和為：

weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0

假設這個神經網路的設計人員選擇以Sigmoid 函式做為啟動函式。在這種情況下，神經元會計算 -2.0 的 Sigmoid 函數，結果約為 0.12。因此，神經元會將 0.12 (而非 -2.0) 傳遞至類神經網路的下一層。下圖說明程序的相關部分：

---

詳情請參閱機器學習速成課程中的「類神經網路：啟動函式」。

人工智慧

#fundamentals

可解決複雜任務的非人類程式或模型。舉例來說，翻譯文字的程式/模型，或是從放射線圖像識別疾病的程式/模型，都展現了人工智慧。

從正式角度來看，機器學習是人工智慧的子領域。不過，近年來有些機構開始交替使用「人工智慧」和「機器學習」這兩個詞彙。

AUC (ROC 曲線下面積)

#fundamentals

#指標

介於 0.0 和 1.0 之間的數字，代表二元分類模型區分正類和負類的能力。AUC 越接近 1.0，代表模型區分各類別的能力越好。

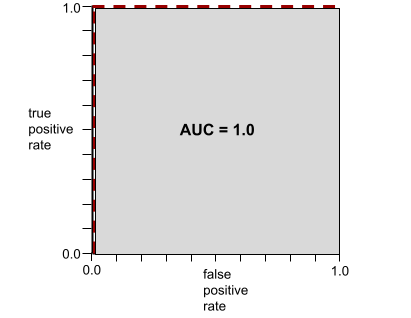
舉例來說，下圖顯示分類模型完美區分正類 (綠色橢圓) 和負類 (紫色矩形)。這個不切實際的完美模型 AUC 值為 1.0：

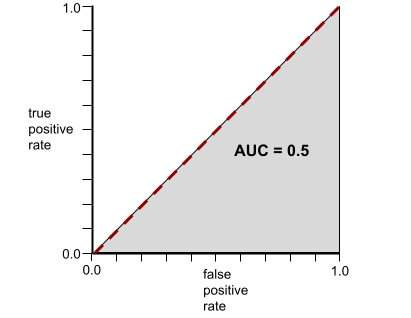
反之，下圖顯示分類模型產生隨機結果時的結果。這個模型的 AUC 為 0.5：

是，前一個模型的 AUC 為 0.5，而非 0.0。

大多數模型都介於這兩個極端之間。舉例來說，下列模型會將正向和負向結果分開，因此 AUC 值介於 0.5 和 1.0 之間：

AUC 會忽略您為分類閾值設定的任何值。AUC 則會考量所有可能的分類門檻。

按一下圖示，瞭解 AUC 和 ROC 曲線之間的關係。

AUC 代表 ROC 曲線下的面積。舉例來說，如果模型能完美區分正類和負類，ROC 曲線會如下所示：

AUC 是上圖中灰色區域的面積。 在這個特殊情況下，面積就是灰色區域的長度 (1.0) 乘以寬度 (1.0)。因此，1.0 和 1.0 的乘積會產生 AUC 值 1.0，這是最高的 AUC 分數。

反之，如果分類模型完全無法區分類別，ROC 曲線如下。這個灰色區域的面積為 0.5。

更典型的 ROC 曲線大致如下所示：

手動計算這條曲線下的面積非常費力，因此通常會由程式計算大多數 AUC 值。

---

按一下圖示，即可查看 AUC 的正式定義。

AUC 是指分類模型認為隨機挑選的正向樣本確實為正向的機率，比隨機挑選的負向樣本為正向的機率還要高。

---

詳情請參閱機器學習速成課程中的「分類：ROC 和 AUC」。

B

反向傳播

#fundamentals

實作梯度下降的演算法，適用於類神經網路。

訓練類神經網路需要多次疊代，才能完成下列雙階段週期：

1. 在正向傳遞期間，系統會處理批次的範例，產生預測結果。系統會比較每個預測值與每個標籤值。預測值與標籤值之間的差異，就是該範例的損失。系統會匯總所有範例的損失，計算目前批次的總損失。
2. 在反向傳播期間，系統會調整所有隱藏層中所有神經元的權重，以減少損失。

類神經網路通常包含許多隱藏層，每個隱藏層都有許多神經元。每個神經元都會以不同方式造成整體損失。 反向傳播會判斷是否要增加或減少套用至特定神經元的權重。

學習率是控制每個反向傳遞增加或減少各權重程度的乘數。如果學習率較高，每個權重的增減幅度會比學習率較低時更大。

以微積分來說，反向傳播會實作微積分的連鎖法則。也就是說，反向傳播會計算相對於每項參數的誤差偏導數。

多年前，機器學習從業人員必須編寫程式碼，才能實作反向傳播。Keras 等現代機器學習 API 現在會為您實作反向傳播。呼！

詳情請參閱機器學習速成課程中的類神經網路。

Batch

#fundamentals

單一訓練疊代中使用的一組範例。批次大小會決定批次中的樣本數量。

如要瞭解批次與紀元的關係，請參閱紀元。

詳情請參閱機器學習速成課程中的「線性迴歸：超參數」。

批次大小

#fundamentals

批次中的樣本數量。 舉例來說，如果批次大小為 100，模型就會在每次疊代時處理 100 個範例。

以下是常見的批次大小策略：

• 隨機梯度下降 (SGD)，批次大小為 1。
• 完整批次：批次大小是整個訓練集中的範例數。舉例來說，如果訓練集包含一百萬個範例，則批次大小為一百萬個範例。完整批次通常是效率不彰的策略。
• 迷你批次，批次大小通常介於 10 到 1000 之間。迷你批次通常是最有效率的策略。

詳情請參閱下列說明文章：

• 機器學習密集課程：可供實際工作環境使用的機器學習系統 - 靜態與動態推論。
• 深度學習調整教戰手冊。

偏誤 (倫理/公平性)

#responsible

#fundamentals

1. 對某些事物、人或群體抱有刻板印象、偏見或偏袒心態。這些偏見可能會影響資料的收集和解讀、系統設計，以及使用者與系統的互動方式。這類偏誤的形式包括：

• 自動化偏誤
• 確認偏誤
• 實驗者偏誤
• 團體歸因偏誤
• 隱性偏誤
• 內團體偏誤
• 外團體同質性偏誤

2. 取樣或通報程序造成的系統性錯誤。這類偏誤的形式包括：

• 涵蓋偏誤
• 無反應偏誤
• 參與偏誤
• 通報偏誤
• 取樣偏誤
• 選擇偏誤

請勿與機器學習模型中的偏誤項或預測偏誤混淆。

詳情請參閱機器學習速成課程的「公平性：偏見類型」。

偏誤 (數學) 或偏誤項

#fundamentals

與原點的截距或偏移量。偏誤是機器學習模型中的參數，以以下任一符號表示：

• b
• w₀

舉例來說，在下列公式中，偏差值是 b：

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

在簡單的二維線中，偏差值只代表「y 截距」。舉例來說，下圖中線條的偏差值為 2。

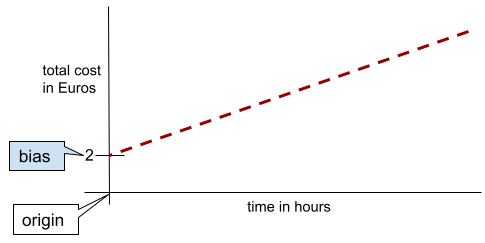
並非所有模型都從原點 (0,0) 開始，因此存在偏差。舉例來說，假設遊樂園的入場費為 2 歐元，顧客每多待一小時就要額外支付 0.5 歐元。因此，對應總成本的模型有 2 歐元的偏差，因為最低成本為 2 歐元。

請勿將偏誤與倫理和公平性方面的偏誤或預測偏誤混淆。

詳情請參閱機器學習速成課程中的「線性迴歸」。

二元分類

#fundamentals

這類分類工作會預測兩個互斥類別之一：

• 正類
• 負類

舉例來說，下列兩個機器學習模型都會執行二元分類：

• 判斷電子郵件是否為垃圾郵件 (正類) 或非垃圾郵件 (負類) 的模型。
• 評估醫療症狀，判斷某人是否罹患特定疾病 (正向類別)，或未罹患該疾病 (負向類別) 的模型。

與多元分類形成對比。

另請參閱邏輯迴歸和分類門檻。

詳情請參閱機器學習密集課程的分類。

資料分組

#fundamentals

將單一特徵轉換為多個二進位特徵，稱為「值區」或「分組」，通常是根據值範圍。切碎的特徵通常是連續特徵。

舉例來說，您可以將溫度範圍切分成離散值，例如：

• 攝氏 10 度以下為「寒冷」類別。
• 攝氏 11 到 24 度則屬於「溫和」類別。
• 攝氏 25 度以上則為「溫暖」類別。

模型會將同一值區中的所有值視為相同。舉例來說，13 和 22 的值都在溫和值區中，因此模型會將這兩個值視為相同。

按一下圖示即可查看其他附註。

如果您將溫度視為連續特徵，模型就會將溫度視為單一特徵。如果將溫度分成三個區間，模型會將每個區間視為個別特徵。也就是說，模型可以學習每個值區與標籤的個別關係。舉例來說，線性迴歸模型可以為每個值區學習不同的權重。

增加 bucket 數量會增加模型必須學習的關係數量，使模型更加複雜。舉例來說，寒冷、溫和和溫暖這三個類別，本質上是模型訓練的三個不同特徵。如果您決定再新增兩個儲存區 (例如冷凍和熱)，模型現在就必須訓練五個不同的特徵。

如何判斷要建立多少個值區，或每個值區的範圍應為何？通常需要進行大量實驗才能找出答案。

---

詳情請參閱機器學習速成課程中的「數值資料：分箱」。

C

類別資料

#fundamentals

特徵具有一組特定可能值。舉例來說，假設有名為 traffic-light-state 的類別特徵，只能有下列三個可能值之一：

• red
• yellow
• green

將 traffic-light-state 視為類別特徵，模型就能瞭解 red、green 和 yellow 對駕駛行為的不同影響。

類別特徵有時也稱為「離散特徵」。

與數值資料形成對比。

詳情請參閱機器學習速成課程的「處理類別資料」。

類別

#fundamentals

標籤所屬的類別。 例如：

• 在偵測垃圾郵件的二元分類模型中，這兩個類別可能是「垃圾郵件」和「非垃圾郵件」。
• 在可辨識犬種的多元分類模型中，類別可能是貴賓犬、米格魯、巴哥犬等。

分類模型會預測類別。相較之下，迴歸模型預測的是數字，而非類別。

詳情請參閱機器學習密集課程的分類。

分類模型

#fundamentals

模型的預測結果為類別。舉例來說，以下都是分類模型：

• 模型會預測輸入句子所用的語言 (法文？西班牙文？ 義大利文？)。
• 預測樹種的模型 (是楓樹嗎？橡木？猴麵包樹？
• 模型會預測特定醫療狀況的正類或負類。

相較之下，迴歸模型預測的是數字，而非類別。

常見的分類模型有兩種：

• 二元分類
• 多元分類

分類門檻

#fundamentals

在二元分類中，介於 0 到 1 之間的數字會將邏輯迴歸模型的原始輸出內容，轉換為正類別或負類別的預測結果。請注意，分類門檻是由人為選擇的值，而非模型訓練選擇的值。

邏輯迴歸模型會輸出介於 0 和 1 之間的原始值。然後：

• 如果這個原始值大於分類門檻，系統就會預測為正類。
• 如果這個原始值小於分類門檻，系統就會預測為負面類別。

舉例來說，假設分類門檻為 0.8。如果原始值為 0.9，模型就會預測正類。如果原始值為 0.7，模型會預測負類。

分類門檻的選擇會大幅影響偽陽性和偽陰性的數量。

按一下圖示即可查看其他附註。

隨著模型或資料集演進，工程師有時也會變更分類閾值。分類閾值變更時，正類預測可能會突然變成負類，反之亦然。

舉例來說，假設您有一個二元分類疾病預測模型。假設系統在第一年執行時：

• 特定病患的原始值為 0.95。
• 分類門檻為 0.94。

因此系統會診斷出正類。(The patient gasps, "Oh no! 我生病了！」)

一年後，這些值可能如下所示：

• 同一位病患的原始值仍為 0.95。
• 分類門檻會變更為 0.97。

因此，系統現在會將該病患重新分類為陰性類別。(「Happy day! 我沒生病。」) 同一位病患。診斷結果不同。

---

詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。

分類器

#fundamentals

分類模型的非正式用語。

不平衡資料集

#fundamentals

如果分類的資料集中，每個類別的標籤總數差異很大，舉例來說，假設有一個二元分類資料集，其中兩個標籤的劃分方式如下：

• 1,000,000 個負值長條標籤
• 10 個正值長條標籤

負面與正面標籤的比例為 100,000 比 1，因此這是類別不平衡的資料集。

相較之下，下列資料集是類別平衡，因為負面標籤與正面標籤的比例相對接近 1：

• 517 個負值標籤
• 483 個正值長條標籤

多類別資料集也可能出現類別不平衡的情況。舉例來說，下列多元分類資料集也屬於類別不平衡，因為其中一個標籤的範例數量遠多於其他兩個：

• 1,000,000 個標籤，類別為「綠色」
• 200 個標籤，類別為「紫色」
• 350 個標籤，類別為「orange」

訓練不平衡資料集可能會遇到特殊挑戰。詳情請參閱機器學習速成課程中的不平衡的資料集。

另請參閱熵、多數類別和少數類別。

剪輯

#fundamentals

處理離群值的技巧，包括執行下列任一或兩項操作：

• 將大於上限門檻的特徵值調降至該上限門檻。
• 將低於最低門檻的特徵值調高至該門檻。

舉例來說，假設特定特徵的值有不到 0.5% 落在 40 到 60 以外的範圍，在這種情況下，您可以採取下列行動：

• 將所有超過 60 (最高門檻) 的值剪輯為 60。
• 將所有低於 40 (最低門檻) 的值剪輯為 40。

離群值可能會損壞模型，有時還會導致訓練期間發生權重溢位。部分離群值也可能大幅影響準確度等指標。剪除是限制損壞的常見技術。

梯度裁剪會在訓練期間，強制將梯度值設在指定範圍內。

詳情請參閱機器學習速成課程中的「數值資料：正規化」。

混淆矩陣

#fundamentals

NxN 表格，彙整分類模型做出的正確和錯誤預測數量。舉例來說，請參考下列二元分類模型的混淆矩陣：

	腫瘤 (預測)	非腫瘤 (預測)
腫瘤 (實際資料)	18 (TP)	1 (FN)
非腫瘤 (基準真相)	6 (FP)	452 (TN)

上述混淆矩陣顯示以下內容：

• 在 19 項基準真相為「腫瘤」的預測中，模型正確分類了 18 項，錯誤分類了 1 項。
• 在 458 項基準真相為「非腫瘤」的預測中，模型正確分類了 452 項，錯誤分類了 6 項。

多類別分類問題的混淆矩陣可協助您找出錯誤模式。舉例來說，假設您有一個 3 類別多類別分類模型，可將三種不同的鳶尾花類型 (Virginica、Versicolor 和 Setosa) 分類，則混淆矩陣如下所示。如果真值是 Virginica，混淆矩陣會顯示模型誤判為 Versicolor 的機率遠高於 Setosa：

	Setosa (預測)	Versicolor (預測)	維吉尼亞州 (預測)
Setosa (真值)	88	12	0
Versicolor (真值)	6	141	7
Virginica (真值)	2	27	109

再舉一例，混淆矩陣可能會顯示，模型在訓練辨識手寫數字時，傾向於誤判 9 而非 4，或誤判 1 而非 7。

混淆矩陣包含充足資訊，可計算各種成效指標，包括精確度和召回率。

連續特徵

#fundamentals

浮點特徵，可能值範圍無限大，例如溫度或重量。

與離散特徵形成對比。

收斂

#fundamentals

當損失值在每次疊代時幾乎沒有變化或完全沒有變化，即達到此狀態。舉例來說，下列損失曲線顯示大約 700 次疊代後會收斂：

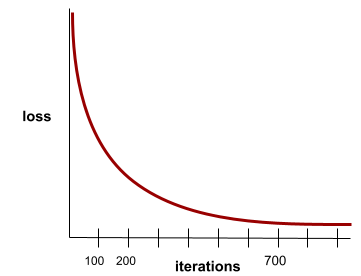
當額外訓練無法改善模型時，模型就會收斂。

在深度學習中，損失值有時會在經過多次疊代後才開始下降，如果長時間出現持續損失值，您可能會暫時產生錯誤的收斂感。

另請參閱「提早停止訓練」。

詳情請參閱機器學習速成課程中的「模型收斂和損失曲線」。

D

DataFrame

#fundamentals

熱門的 pandas 資料型別，用於表示記憶體中的資料集。

DataFrame 類似於表格或試算表，DataFrame 的每個資料欄都有名稱 (標題)，每個資料列則由專屬號碼識別。

DataFrame 中的每個資料欄都採用二維陣列結構，但每個資料欄可指派自己的資料型別。

另請參閱官方的 pandas.DataFrame 參考資料頁面。

資料集

#fundamentals

原始資料集合，通常 (但不一定) 會以下列其中一種格式整理：

• 試算表
• CSV (半形逗號分隔值) 格式的檔案

深度模型

#fundamentals

含有多個隱藏層的類神經網路。

深層模型也稱為深層類神經網路。

與寬模型相比。

稠密特徵

#fundamentals

特徵，其中大部分或所有值都是非零值，通常是浮點值的 Tensor。舉例來說，下列 10 元素張量是密集張量，因為其中 9 個值不為零：

8

3

7

5

2

4

0

4

9

6

與稀疏特徵形成對比。

深度

#fundamentals

類神經網路中的下列項目總和：

• 隱藏層的數量
• 輸出層的數量，通常為 1
• 任意嵌入層的數量

舉例來說，如果類神經網路有五個隱藏層和一個輸出層，深度就是 6。

請注意，輸入層不會影響深度。

離散特徵

#fundamentals

特徵具有一組有限的可能值。舉例來說，如果特徵的值只能是「動物」、「蔬菜」或「礦物」，則該特徵就是離散 (或類別) 特徵。

與連續性特徵形成對比。

動態

#fundamentals

經常或持續進行的動作。 在機器學習中，「動態」和「線上」是同義詞。 以下是機器學習中 dynamic 和 online 的常見用途：

• 動態模型 (或線上模型) 是指經常或持續重新訓練的模型。
• 動態訓練 (或線上訓練) 是指頻繁或持續訓練的過程。
• 動態推論 (或線上推論) 是指依需求產生預測的程序。

動態模型

#fundamentals

經常 (甚至持續) 重新訓練的模型。動態模型是「終身學習者」，會不斷適應不斷變化的資料。動態模型也稱為線上模型。

與靜態模型形成對比。

E

提早停止

#fundamentals

一種正規化方法，包括在訓練損失減少前結束訓練。在提早停止訓練中，當驗證資料集的損失開始增加時，您會刻意停止訓練模型；也就是一般化效能變差時。

按一下圖示即可查看其他附註。

提早停止訓練看似違反直覺，畢竟，如果損失仍在減少，就要求模型停止訓練，可能就像要求廚師在甜點完全烤好前停止烹調。不過，訓練模型的時間過長可能會導致過度配適。也就是說，如果訓練模型的時間過長，模型可能會過度配適訓練資料，導致無法準確預測新樣本。

---

與提早結束形成對比。

嵌入層

#fundamentals

這是一種特殊的隱藏層，會訓練高維度類別特徵，逐步學習低維度嵌入向量。與僅以高維度類別特徵進行訓練相比，嵌入層可讓類神經網路更有效率地訓練。

舉例來說，Google 地球目前支援約 73,000 種樹木。假設樹種是模型中的特徵，則模型的輸入層會包含 73,000 個元素的單熱向量。舉例來說，baobab 可能會以類似下列方式表示：

73,000 個元素的陣列非常長。如果沒有在模型中加入嵌入層，由於要乘上 72,999 個零，訓練過程會非常耗時。假設您選擇的嵌入層包含 12 個維度。因此，嵌入層會逐步學習每種樹木的新嵌入向量。

在某些情況下，雜湊是合理的替代方案，可取代嵌入層。

詳情請參閱機器學習速成課程中的「嵌入」一文。

Epoch 紀元時間

#fundamentals

完整訓練過程會處理整個訓練集，每個範例都會處理一次。

一個訓練週期代表 N/批量 訓練疊代，其中 N 是樣本總數。

舉例來說，假設：

• 資料集包含 1,000 個範例。
• 批次大小為 50 個範例。

因此，單一訓練週期需要 20 次疊代：

1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations

詳情請參閱機器學習速成課程中的「線性迴歸：超參數」。

範例

#fundamentals

特徵的一列值，以及可能的標籤。監督式學習的範例大致可分為兩類：

• 標示範例包含一或多個特徵和標籤。訓練期間會使用標記範例。
• 未標記的範例包含一或多個特徵，但不含標籤。推論期間會使用未加上標籤的樣本。

舉例來說，假設您要訓練模型，判斷天氣狀況對學生測驗成績的影響。以下是三個標示範例：

功能			標籤
溫度	溼度	氣壓	測驗分數
15	47	998	不錯
19	34	1020	極佳
18	92	1012	不佳

以下是三個未標記的範例：

溫度	溼度	氣壓
12	62	1014
21	47	1017
19	41	1021

資料集的資料列通常是範例的原始來源。 也就是說，範例通常包含資料集中的部分資料欄。此外，範例中的特徵也可以包含合成特徵，例如特徵交叉。

詳情請參閱「機器學習簡介」課程中的「監督式學習」。

F

偽陰性 (FN)

#fundamentals

#指標

模型錯誤預測負類的例子。舉例來說，模型預測某封電子郵件不是垃圾郵件 (負面類別)，但該郵件實際上是垃圾郵件。

偽陽性 (FP)

#fundamentals

#指標

舉例來說，模型錯誤預測正類。舉例來說，模型預測特定電子郵件是垃圾郵件 (正類)，但該電子郵件其實不是垃圾郵件。

詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。

偽陽率 (FPR)

#fundamentals

#指標

模型錯誤預測為正類的實際負例比例。下列公式可計算出誤報率：

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

偽陽率是 ROC 曲線的 x 軸。

詳情請參閱機器學習速成課程中的「分類：ROC 和 AUC」。

功能

#fundamentals

機器學習模型的輸入變數。範例包含一或多個特徵。舉例來說，假設您要訓練模型，判斷天氣狀況對學生測驗成績的影響。下表顯示三個範例，每個範例都包含三個特徵和一個標籤：

功能			標籤
溫度	溼度	氣壓	測驗分數
15	47	998	92
19	34	1020	84
18	92	1012	87

與標籤的對比度。

詳情請參閱「機器學習簡介」課程中的「監督式學習」。

特徵交錯

#fundamentals

由「交錯組合」類別或值區化特徵形成的合成特徵。

舉例來說，假設「情緒預測」模型會將溫度歸入下列四個類別之一：

• freezing
• chilly
• temperate
• warm

並以以下三種其中一種方式表示風速：

• still
• light
• windy

如果沒有特徵交叉，線性模型會針對上述七個不同區隔分別進行訓練。因此，模型會根據 freezing 訓練，例如，windy 的訓練與前者無關。

或者，您也可以建立溫度和風速的特徵交叉項。這個合成特徵會有下列 12 個可能值：

• freezing-still
• freezing-light
• freezing-windy
• chilly-still
• chilly-light
• chilly-windy
• temperate-still
• temperate-light
• temperate-windy
• warm-still
• warm-light
• warm-windy

透過特徵交叉，模型可以瞭解freezing-windy天和freezing-still天之間的情緒差異。

如果您從兩個各有很多不同值區的特徵建立合成特徵，產生的特徵交叉會出現大量可能的組合。舉例來說，如果一個特徵有 1,000 個值區，另一個特徵有 2,000 個值區，則產生的特徵交叉有 2,000,000 個值區。

正式來說，交叉是笛卡兒乘積。

特徵交叉通常用於線性模型，很少用於類神經網路。

詳情請參閱機器學習速成課程中的「類別資料：特徵交叉」。

特徵工程

#fundamentals

#TensorFlow

這項程序包含下列步驟：

1. 判斷哪些特徵可能適合用來訓練模型。
2. 將資料集中的原始資料轉換為這些特徵的有效版本。

舉例來說，您可能會判斷 temperature 是實用的功能。接著，您可以嘗試分組，最佳化模型從不同 temperature 範圍學習的內容。

特徵工程有時也稱為「特徵擷取」或「特徵化」。

按一下圖示，即可查看 TensorFlow 的其他附註。

在 TensorFlow 中，特徵工程通常是指將原始記錄檔項目轉換為 tf.Example 通訊協定緩衝區。另請參閱 tf.Transform。

---

詳情請參閱機器學習速成課程中的「數值資料：模型如何使用特徵向量擷取資料」。

功能集

#fundamentals

機器學習模型訓練時所用的特徵群組。舉例來說，預測房價的模型可能只會使用郵遞區號、房產大小和房產狀況等簡單特徵。

特徵向量

#fundamentals

包含特徵值的陣列，組成範例。特徵向量會在訓練和推論期間輸入。 舉例來說，如果模型有兩個不連續的特徵，特徵向量可能如下：

[0.92, 0.56]

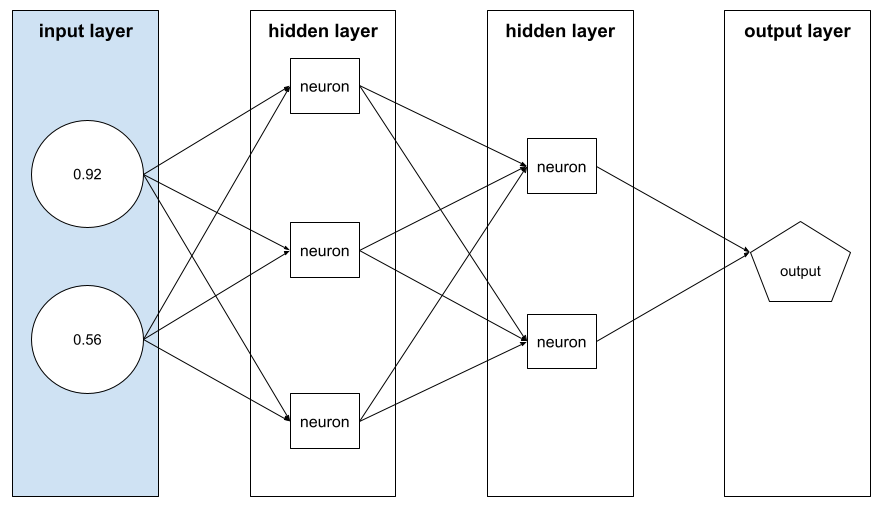
每個範例都會提供特徵向量的不同值，因此下一個範例的特徵向量可能是：

[0.73, 0.49]

特徵工程會決定如何在特徵向量中表示特徵。舉例來說，具有五個可能值的二元類別特徵，可以透過 one-hot 編碼表示。在本例中，特定範例的特徵向量部分會包含四個零，以及第三個位置的單一 1.0，如下所示：

[0.0, 0.0, 1.0, 0.0, 0.0]

再舉一例，假設您的模型包含三項特徵：

• 以 one-hot 編碼表示的二元類別特徵，具有五個可能值，例如：[0.0, 1.0, 0.0, 0.0, 0.0]
• 另一個二元類別特徵，有 三個可能值，以 one-hot 編碼表示，例如：[0.0, 0.0, 1.0]
• 浮點特徵，例如：8.3。

在此情況下，每個範例的特徵向量會以九個值表示。根據上述清單中的範例值，特徵向量會是：

0.0
1.0
0.0
0.0
0.0
0.0
0.0
1.0
8.3

詳情請參閱機器學習速成課程中的「數值資料：模型如何使用特徵向量擷取資料」。

回饋循環

#fundamentals

在機器學習中，模型預測結果會影響同一模型或其他模型的訓練資料。舉例來說，推薦電影的模型會影響使用者看到的電影，進而影響後續的電影推薦模型。

詳情請參閱機器學習速成課程中的「可供實際工作環境使用的機器學習系統：應提出的問題」。

G

一般化

#fundamentals

模型對先前未見過的新資料做出正確預測的能力。能夠泛化的模型與過度配適的模型相反。

按一下圖示即可查看其他附註。

您會根據訓練集中的範例訓練模型。因此，模型會學習訓練集中的資料特徵。泛化基本上是詢問模型是否能對不在訓練集中的樣本做出準確預測。

為鼓勵泛化，正規化有助於模型訓練，減少訓練集資料特徵的影響。

---

詳情請參閱機器學習速成課程中的「一般化」。

一般化曲線

#fundamentals

以疊代次數為函式，繪製訓練損失和驗證損失的圖表。

一般化曲線有助於偵測可能的過度訓練。舉例來說，下列一般化曲線顯示過度訓練，因為驗證損失最終會明顯高於訓練損失。

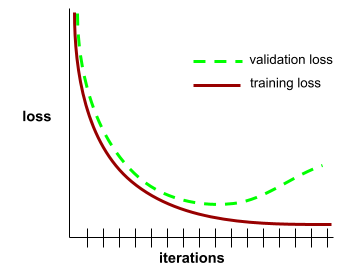
詳情請參閱機器學習速成課程中的「一般化」。

梯度下降

#fundamentals

這項數學技術可盡量減少損失。 梯度下降會反覆調整權重和偏差，逐步找出可將損失降至最低的最佳組合。

梯度下降法比機器學習更古老，而且古老得多。

詳情請參閱機器學習速成課程中的「線性迴歸：梯度下降」。

真值

#fundamentals

實境。

實際發生的情況。

舉例來說，假設有一個二元分類模型，可預測大學一年級學生是否會在六年內畢業。這個模型的實際資料是學生是否在六年內畢業。

按一下圖示即可查看其他附註。

我們會根據基準真相評估模型品質。不過，基準真相不一定完全真實。舉例來說，請參考下列範例，瞭解實際情況可能出現的瑕疵：

• 在畢業範例中，我們確定每位學生的畢業記錄一律正確嗎？大學的記錄是否完美無缺？
• 假設標籤是儀器 (例如氣壓計) 測量的浮點值。如何確保每部儀器都經過相同校正，或每次讀取資料時的環境條件都相同？
• 如果標籤是人類的意見，如何確保每位評估人員都以相同方式評估事件？為提升一致性，有時會由專家人工評估員介入。

---

H

隱藏層

#fundamentals

類神經網路中，介於輸入層 (特徵) 和輸出層 (預測) 之間的層。每個隱藏層都包含一或多個神經元。 舉例來說，下列類神經網路包含兩個隱藏層，第一個隱藏層有三個神經元，第二個隱藏層有兩個神經元：

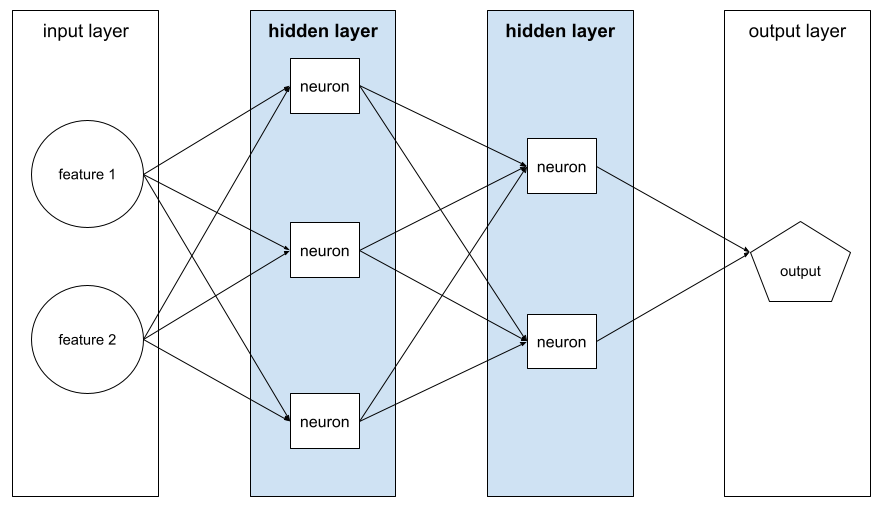
深層類神經網路包含多個隱藏層。舉例來說，上圖是深層類神經網路，因為模型包含兩個隱藏層。

詳情請參閱機器學習速成課程中的「類神經網路：節點和隱藏層」。

超參數

#fundamentals

您或超參數調整服務 (例如 Vizier) 在連續執行模型訓練時調整的變數。舉例來說，學習率就是超參數。您可以在訓練階段開始前，將學習率設為 0.01。如果認為 0.01 太高，或許可以在下一個訓練工作階段將學習率設為 0.003。

相反地，參數是模型在訓練期間學習的各種權重和偏差。

詳情請參閱機器學習速成課程中的「線性迴歸：超參數」。

I

獨立同分布 (i.i.d)

#fundamentals

從不會變更的分配方式中提取資料，且提取的每個值都不會取決於先前提取的值。獨立且相同分布 (i.i.d.) 是機器學習的理想氣體，也就是實用的數學建構，但現實世界中幾乎不會完全符合。舉例來說，網頁訪客的分配情形在短時間內可能呈現 i.i.d.，也就是說，分配情形在短時間內不會改變，而且一個人的造訪行為通常不會影響另一個人的造訪行為。不過，如果擴大時間範圍，網頁訪客人數可能會出現季節性差異。

另請參閱非平穩性。

推論

#fundamentals

#generativeAI

在傳統機器學習中，將訓練好的模型套用至未標記的範例，藉此進行預測的過程。如要瞭解詳情，請參閱「機器學習簡介」課程中的「監督式學習」。

在大型語言模型中，推論是指使用訓練好的模型，針對輸入的提示生成回覆的過程。

在統計學中，「推論」的意義略有不同。詳情請參閱 有關統計推論的維基百科文章。

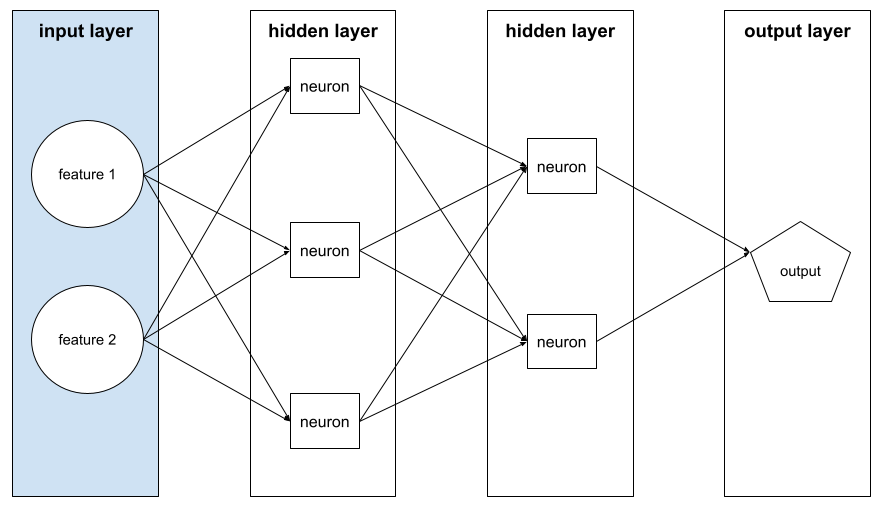
輸入層

#fundamentals

類神經網路的層會儲存特徵向量。也就是說，輸入層會提供範例，用於訓練或推論。舉例來說，下列神經網路的輸入層包含兩項特徵：

可解釋性

#fundamentals

以人類可理解的用語，說明或呈現機器學習模型的推理過程。

舉例來說，大多數線性迴歸模型都具有高度可解讀性。(您只需查看每個特徵的訓練權重)。決策樹林也具有高度可解讀性。不過，部分模型仍需轉繪成複雜的圖表，才具有可解釋性。

您可以使用學習技術可解釋性工具 (LIT) 解讀機器學習模型。

疊代

#fundamentals

在訓練期間，模型參數 (即模型的權重和偏差) 的單一更新。批次大小會決定模型在單次疊代中處理的樣本數量。舉例來說，如果批次大小為 20，模型會先處理 20 個範例，再調整參數。

訓練類神經網路時，單一疊代會涉及下列兩次傳遞：

1. 前向傳遞，用於評估單一批次的損失。
2. 反向傳播 (反向傳播)，根據損失和學習率調整模型參數。

詳情請參閱機器學習密集課程中的梯度下降。

L

L₀ 正則化

#fundamentals

一種正規化類型，會懲罰模型中非零權重的總數。舉例來說，如果模型有 11 個非零權重，受到的懲罰會比有 10 個非零權重的類似模型更重。

L₀ 正則化有時也稱為 L0 範數正則化。

按一下圖示即可查看其他附註。

一般來說，L₀ 正則化不適用於大型模型，因為 L₀ 正則化會將訓練變成凸面最佳化問題。

---

L₁ 損失

#fundamentals

#指標

損失函式，用於計算實際標籤值與模型預測值之間的絕對差異。舉例來說，以下是五個範例的批次 L₁ 損失計算：

範例的實際值	模型預測值	差異的絕對值
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 損失

相較於 L₂ 損失，L₁ 損失對離群值的敏感度較低。

平均絕對誤差是每個樣本的平均 L₁ 損失。

按一下圖示即可查看正式數學式。

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

其中：

• $n$ 是範例數。
• $y$ 是標籤的實際值。
• $\hat{y}$ 是模型預測的 $y$ 值。

---

詳情請參閱機器學習速成課程中的「線性迴歸：損失」。

L₁ 正則化

#fundamentals

一種正規化，會根據權重絕對值的總和，按比例進行加權。L₁ 正則化有助於將不相關或幾乎不相關特徵的權重設為 0。如果特徵的權重為 0，模型就會有效移除該特徵。

與 L₂ 正則化的差異。

L₂ 損失

#fundamentals

#指標

損失函式：計算實際標籤值與模型預測值之間的差異平方。舉例來說，以下是五個範例的批次 L₂ 損失計算：

範例的實際值	模型預測值	Delta 的平方
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = L2 損失

由於平方運算，L₂ 損失會放大離群值的影響。也就是說，相較於 L₁ 損失，L₂ 損失對錯誤預測的反應更強烈。舉例來說，前述批次的 L₁ 損失會是 8 而不是 16。請注意，單一離群值就占了 16 個中的 9 個。

迴歸模型通常會使用 L₂ 損失做為損失函式。

均方誤差是每個樣本的平均 L₂ 損失。平方損失是 L₂ 損失的別名。

按一下圖示即可查看正式數學式。

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

其中：

• $n$ 是範例數。
• $y$ 是標籤的實際值。
• $\hat{y}$ 是模型預測的 $y$ 值。

---

詳情請參閱機器學習速成課程中的「邏輯迴歸：損失和正規化」。

L₂ 正則化

#fundamentals

一種正規化，會根據權重平方的總和，按比例懲罰權重。L₂ 正則化有助於將離群值權重 (高正值或低負值) 調整為接近 0，但不會完全為 0。值非常接近 0 的特徵仍會保留在模型中，但對模型預測的影響不大。

L₂ 正則化一律可改善線性模型的一般化作業。

與 L₁ 正則化的差異。

詳情請參閱機器學習速成課程中的「過度擬合：L2 正規化」。

標籤

#fundamentals

在監督式機器學習中，範例的「答案」或「結果」部分。

每個標示範例都包含一或多個特徵和標籤。舉例來說，在垃圾內容偵測資料集中，標籤可能是「垃圾內容」或「非垃圾內容」。在降雨資料集中，標籤可能是指特定期間的降雨量。

詳情請參閱「機器學習簡介」中的「監督式學習」。

有標籤樣本

#fundamentals

包含一或多個特徵和標籤的範例。舉例來說，下表顯示房屋估價模型中的三個標籤範例，每個範例都包含三項特徵和一個標籤：

臥室數量	浴室數量	房屋屋齡	房屋價格 (標籤)
3	2	15	$345,000
2	1	72	$179,000
4	2	34	$392,000

在監督式機器學習中，模型會根據加上標籤的樣本進行訓練，並對未加上標籤的樣本做出預測。

對比有標籤和無標籤的範例。

詳情請參閱「機器學習簡介」中的「監督式學習」。

lambda

#fundamentals

正規化率的同義詞。

Lambda 是過載的字詞。本文將著重於正規化中的定義。

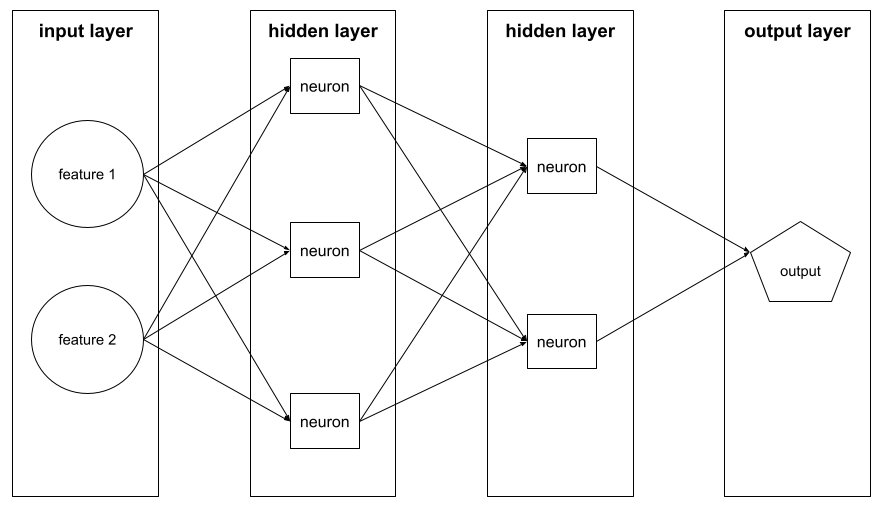
圖層

#fundamentals

類神經網路中的一組神經元。以下是三種常見的圖層類型：

• 輸入層，提供所有特徵的值。
• 一或多個隱藏層，可找出特徵與標籤之間的非線性關係。
• 輸出層：提供預測結果。

舉例來說，下圖顯示的類神經網路包含一個輸入層、兩個隱藏層和一個輸出層：

在 TensorFlow 中，層也是 Python 函式，會將 Tensor 和設定選項做為輸入內容，並產生其他張量做為輸出內容。

學習率

#fundamentals

浮點數，可告知梯度下降演算法，在每次疊代時，權重和偏差值的調整幅度。舉例來說，如果學習率為 0.3，權重和偏差的調整幅度會是學習率 0.1 的三倍。

學習率是重要的超參數。如果學習率設定過低，訓練時間會太長。如果學習率設定過高，梯度下降通常難以達到收斂。

按一下圖示，即可查看更詳細的數學說明。

在每次疊代期間，梯度下降演算法會將學習率乘以梯度。產生的結果稱為「梯度步長」。

---

詳情請參閱機器學習速成課程中的「線性迴歸：超參數」。

線性

#fundamentals

兩個或多個變數之間的關係，只能透過加法和乘法表示。

線性關係的圖表是直線。

與非線性比較。

線性模式

#fundamentals

模型：為每個特徵指派一個權重，以進行預測。(線性模型也會納入偏差。) 相較之下，深層模型中特徵與預測結果的關係通常是非線性。

相較於深層模型，線性模型通常更容易訓練，且可解讀性更高。不過，深層模型可以學習特徵之間的複雜關係。

線性迴歸和邏輯迴歸是兩種線性模型。

按一下圖示即可查看數學式。

線性模型遵循下列公式：

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

其中：

• y' 是原始預測結果。(在某些類型的線性模型中，這項原始預測結果會進一步修改。(例如，請參閱邏輯迴歸)。
• b 是偏誤。
• w 是權重，因此 w₁ 是第一個特徵的權重，w₂ 是第二個特徵的權重，依此類推。
• x 是特徵，因此 x₁ 是第一個特徵的值，x₂ 是第二個特徵的值，依此類推。

舉例來說，假設有三個特徵的線性模型學習到下列偏差和權重：

• b = 7
• w₁ = -2.5
• w₂ = -1.2
• w₃ = 1.4

因此，如果提供三個特徵 (x₁、x₂ 和 x₃)，線性模型會使用下列方程式產生每項預測：

y' = 7 + (-2.5)(x1) + (-1.2)(x2) + (1.4)(x3)

假設特定範例包含下列值：

• x₁ = 4
• x₂ = -10
• x₃ = 5

將這些值代入公式，即可得出這個範例的預測結果：

y' = 7 + (-2.5)(4) + (-1.2)(-10) + (1.4)(5)
y' = 16

線性模型不僅包含僅使用線性方程式進行預測的模型，也包含更廣泛的模型，這些模型使用線性方程式做為預測公式的其中一個元件。舉例來說，邏輯迴歸會後續處理原始預測值 (y')，產生介於 0 和 1 之間的最終預測值 (不含 0 和 1)。

---

線性迴歸

#fundamentals

這類機器學習模型符合下列條件：

• 這個模型是線性模型。
• 預測值為浮點數值。(這是線性迴歸的迴歸部分。)

比較線性迴歸與邏輯迴歸。此外，請比較迴歸與分類。

詳情請參閱機器學習速成課程中的線性迴歸。

邏輯迴歸

#fundamentals

這是一種迴歸模型，可預測機率。邏輯迴歸模型具有下列特性：

• 標籤為類別。邏輯迴歸一詞通常是指二元邏輯迴歸，也就是計算標籤機率的模型，標籤有兩個可能的值。多項式邏輯迴歸是較不常見的變體，可計算標籤的機率，適用於有兩個以上可能值的情況。
• 訓練期間的損失函式為 Log Loss。 (如果標籤有兩個以上的可能值，可以並行放置多個 Log Loss 單位)。
• 模型採用線性架構，而非深層類神經網路。 不過，這項定義的其餘部分也適用於深層模型，這類模型會預測類別標籤的機率。

舉例來說，假設有一個邏輯迴歸模型，會計算輸入電子郵件是垃圾郵件或非垃圾郵件的機率。在推論期間，假設模型預測值為 0.72。因此，模型會估算：

• 這封電子郵件有 72% 的機率是垃圾郵件。
• 這封電子郵件有 28% 的機率不是垃圾郵件。

邏輯迴歸模型採用下列兩步驟架構：

1. 模型會套用輸入特徵的線性函式，產生原始預測結果 (y')。
2. 模型會將原始預測結果做為 S 函數的輸入，將原始預測結果轉換為介於 0 到 1 之間的值 (不含 0 和 1)。

與任何迴歸模型一樣，邏輯迴歸模型會預測數字。 不過，這個數字通常會成為二元分類模型的一部分，如下所示：

• 如果預測值大於分類門檻，二元分類模型就會預測正類。
• 如果預測的數字小於分類門檻，二元分類模型會預測負類。

詳情請參閱機器學習速成課程中的邏輯迴歸。

對數損失

#fundamentals

用於二元邏輯迴歸的損失函式。

按一下圖示即可查看數學式。

下列公式會計算對數損失：

$$\text{Log Loss} = \sum_{(x,y)\in D} -y\log(y') - (1 - y)\log(1 - y')$$

其中：

• \((x,y)\in D\) 是包含許多已加上標籤的範例 (即 \((x,y)\) 配對) 的資料集。
• \(y\) 是有標籤樣本中的標籤。由於這是邏輯迴歸， \(y\) 的每個值都必須是 0 或 1。
• \(y'\) 是預測值 (介於 0 和 1 之間，不含 0 和 1)， \(x\)則是一組特徵。

---

詳情請參閱機器學習速成課程中的邏輯迴歸：損失和正規化。

對數勝算比

#fundamentals

某個事件發生機率的對數。

按一下圖示即可查看數學式。

如果事件是二元機率，則「勝算」是指成功機率 (p) 與失敗機率 (1-p) 的比率。舉例來說，假設某個事件的成功機率為 90%，失敗機率為 10%。在本例中，賠率的計算方式如下：

$$ {\text{odds}} = \frac{\text{p}} {\text{(1-p)}} = \frac{.9} {.1} = {\text{9}} $$

對數勝算比就是勝算比的對數。按照慣例，「對數」是指自然對數，但對數的底數實際上可以是任何大於 1 的數字。按照慣例，我們範例的對數勝算為：

$$ {\text{log-odds}} = ln(9) ~= 2.2 $$

對數勝算函式是S 函數的反函式。

---

損失

#fundamentals

#指標

在訓練監督式模型時，會測量模型預測與標籤之間的差距。

損失函數會計算損失。

詳情請參閱機器學習速成課程中的「線性迴歸：損失」。

損失曲線

#fundamentals

以訓練疊代次數為函數的損失圖。下圖顯示典型的損失曲線：

損失曲線有助於判斷模型何時收斂或過度擬合。

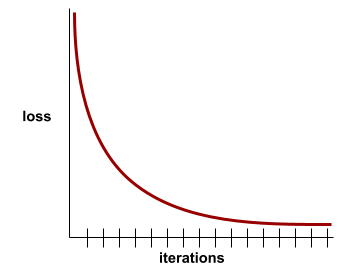
損失曲線可繪製下列所有類型的損失：

• 訓練損失
• 驗證損失
• 測試損失

另請參閱一般化曲線。

詳情請參閱機器學習速成課程中的「過度擬合：解讀損失曲線」。

損失函數

#fundamentals

#指標

在訓練或測試期間，計算批次範例損失的數學函式。如果模型預測結果良好，損失函式會傳回較低的損失值；如果模型預測結果不佳，則會傳回較高的損失值。

訓練的目標通常是盡量減少損失函式傳回的損失。

損失函數的種類繁多，請為您要建構的模型類型選擇適當的損失函數。例如：

• L₂ 損失 (或均方誤差) 是線性迴歸的損失函式。
• 對數損失是邏輯迴歸的損失函數。

M

機器學習

#fundamentals

根據輸入資料訓練模型的程式或系統。訓練好的模型能根據全新或未知資料進行實用預測，這些資料的分布情形與訓練模型時使用的資料相同。

機器學習也指涉與這些程式或系統相關的研究領域。

詳情請參閱「機器學習簡介」課程。

多數類別

#fundamentals

不平衡資料集中較常見的標籤。舉例來說，如果資料集中有 99% 的負向標籤和 1% 的正向標籤，負向標籤就是多數類別。

與少數類別形成對比。

詳情請參閱機器學習速成課程中的「資料集：不平衡的資料集」。

小批

#fundamentals

在一次疊代中處理的批次資料中，隨機選取的一小部分。迷你批次的批次大小通常介於 10 到 1,000 個樣本之間。

舉例來說，假設整個訓練集 (完整批次) 包含 1,000 個範例。假設您將每個迷你批次的批次大小設為 20。因此，每次疊代都會從 1,000 個範例中隨機選取 20 個，判斷損失，然後據此調整權重和偏差。

計算迷你批次的損失，比計算完整批次中所有範例的損失更有效率。

詳情請參閱機器學習速成課程中的「線性迴歸：超參數」。

少數類別

#fundamentals

在類別不平衡的資料集中，較不常見的標籤。舉例來說，假設資料集包含 99% 的負面標籤和 1% 的正面標籤，則正面標籤屬於少數類別。

與多數類別形成對比。

按一下圖示即可查看其他附註。

擁有 100 萬個範例的訓練集聽起來很厲害，不過，如果少數類別的代表性不佳，即使訓練集非常龐大，可能也不足。請減少對資料集中樣本總數的關注，多注意少數類別中的樣本數量。

如果資料集中沒有足夠的少數類別範例，請考慮使用下採樣 (第二個項目符號中的定義) 補充少數類別。

---

詳情請參閱機器學習速成課程中的「資料集：不平衡的資料集」。

模型

#fundamentals

一般來說，任何可處理輸入資料並傳回輸出內容的數學建構體，換句話說，模型是系統進行預測所需的一組參數和結構。在監督式機器學習中，模型會將範例做為輸入內容，並推斷預測結果做為輸出內容。在監督式機器學習中，模型會有些許差異。例如：

• 線性迴歸模型由一組權重和偏差組成。
• 類神經網路模型包含：
  • 一組隱藏層，每個隱藏層都包含一或多個神經元。
  • 與每個神經元相關聯的權重和偏差。
• 決策樹模型包含：
  • 樹狀結構的形狀，也就是條件和葉節點的連結模式。
  • 條件和葉片。

您可以儲存、還原或複製模型。

非監督式機器學習也會產生模型，通常是可將輸入範例對應至最合適叢集的函式。

按一下圖示，比較代數和程式設計函式與機器學習模型。

下列代數函式就是模型：

  f(x, y) = 3x -5xy + y2 + 17

上述函式會將輸入值 (x 和 y) 對應至輸出。

同樣地，下列程式設計函式也是模型：

def half_of_greater(x, y):
  if (x > y):
    return(x / 2)
  else
    return(y / 2)

呼叫端會將引數傳遞至上述 Python 函式，而 Python 函式會產生輸出內容 (透過 return 陳述式)。

雖然深層類神經網路的數學結構與代數或程式設計函式大不相同，但深層類神經網路仍會接收輸入內容 (範例) 並傳回輸出內容 (預測)。

人類程式設計師會手動編寫程式設計函式。相較之下，機器學習模型會在自動訓練期間，逐步學習最佳參數。

---

多元分類

#fundamentals

在監督式學習中，資料集包含兩個以上的標籤類別，因此屬於分類問題。舉例來說，Iris 資料集中的標籤必須是下列三種類別之一：

• Iris setosa
• Iris virginica
• 雜色鳶尾

以 Iris 資料集訓練的模型會預測新樣本的 Iris 類型，並執行多元分類。

相反地，如果分類問題要區分兩個類別，則屬於二元分類模型。舉例來說，如果電子郵件模型預測結果為「垃圾郵件」或「非垃圾郵件」，就是二元分類模型。

在叢集問題中，多元分類是指兩個以上的叢集。

詳情請參閱機器學習速成課程中的「類神經網路：多類別分類」。

否

負類

#fundamentals

#指標

在二元分類中，一個類別稱為「正類」，另一個類別則稱為「負類」。正類是模型測試的項目或事件，負類則是其他可能性。例如：

• 醫療檢測中的負面類別可能是「非腫瘤」。
• 在電子郵件分類模型中，負面類別可能是「非垃圾郵件」。

與正類形成對比。

輸出內容

#fundamentals

包含至少一個隱藏層的模型。深層類神經網路是一種類神經網路，含有多個隱藏層。舉例來說，下圖顯示包含兩個隱藏層的深層類神經網路。

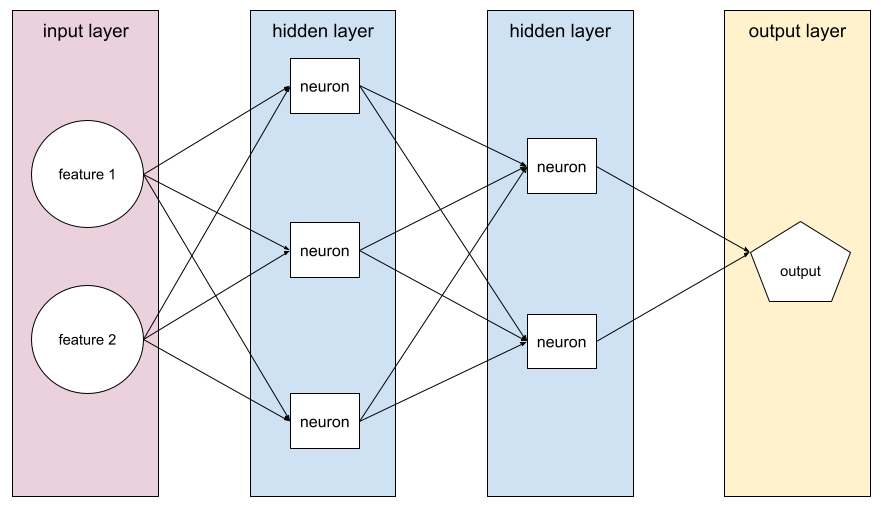
類神經網路中的每個神經元都會連結至下一層的所有節點。舉例來說，在上圖中，請注意第一個隱藏層中的三個神經元，分別連線至第二個隱藏層中的兩個神經元。

在電腦上實作的類神經網路有時稱為「人工類神經網路」，以區別於大腦和其他神經系統中的類神經網路。

部分類神經網路可以模擬不同特徵與標籤之間極為複雜的非線性關係。

另請參閱卷積類神經網路和循環類神經網路。

詳情請參閱機器學習速成課程中的類神經網路。

神經元

#fundamentals

在機器學習中，類神經網路隱藏層內的獨立單元。每個神經元會執行下列兩步驟動作：

1. 計算輸入值乘以對應權重的加權總和。
2. 將加權總和做為輸入內容，傳遞至啟動函式。

第一個隱藏層中的神經元會接受輸入層中的特徵值輸入。第一個隱藏層之後的任何隱藏層神經元，都會接受前一個隱藏層神經元的輸入內容。舉例來說，第二個隱藏層中的神經元會接受第一個隱藏層中神經元的輸入內容。

下圖標示出兩個神經元及其輸入內容。

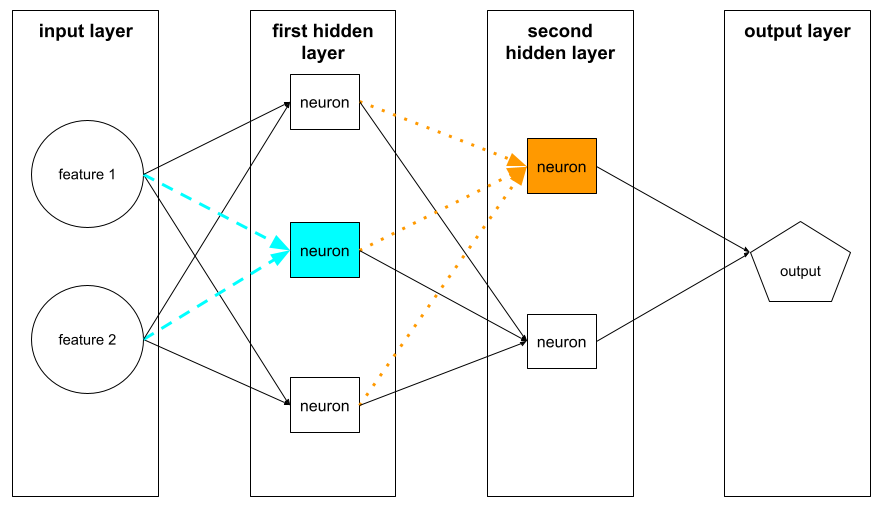
類神經網路中的神經元會模擬大腦和其他神經系統部位的神經元行為。

節點 (類神經網路)

#fundamentals

隱藏層中的神經元。

詳情請參閱機器學習速成課程中的「類神經網路」。

非線性

#fundamentals

兩個或多個變數之間的關係，無法單純透過加法和乘法表示。線性關係可以表示為一條線，非線性關係則無法表示為一條線。舉例來說，假設有兩個模型，分別將單一特徵與單一標籤建立關聯。左側模型為線性，右側模型為非線性：

如要試用各種非線性函式，請參閱機器學習速成課程中的「類神經網路：節點和隱藏層」。

非平穩性

#fundamentals

值會在一或多個維度 (通常是時間) 之間變更的特徵。舉例來說，請參考下列非平穩性範例：

• 特定商店的泳衣銷售量會因季節而異。
• 特定區域在一年中的大部分時間，某種水果的收成量為零，但短時間內收成量很大。
• 由於氣候變遷，年平均溫度正在轉移。

與平穩性形成對比。

正規化

#fundamentals

廣義來說，將變數的實際值範圍轉換為標準值範圍的過程，例如：

• -1 至 +1
• 0 至 1
• Z 分數 (約 -3 至 +3)

舉例來說，假設某個特徵的實際值範圍是 800 到 2,400，在特徵工程中，您可以將實際值正規化為標準範圍，例如 -1 到 +1。

在特徵工程中，正規化是常見的工作。如果特徵向量中的每個數值特徵大致上都屬於相同範圍，模型通常會訓練得更快 (並產生更準確的預測)。

另請參閱 Z 分數正規化。

詳情請參閱機器學習速成課程中的「數值資料：正規化」。

數值資料

#fundamentals

以整數或實數表示的特徵。舉例來說，房屋估價模型可能會將房屋大小 (以平方英尺或平方公尺為單位) 表示為數值資料。將特徵表示為數值資料，表示特徵值與標籤之間存在數學關係。也就是說，房屋的平方公尺數可能與房屋價值存在某種數學關係。

並非所有整數資料都應以數值資料表示。舉例來說，世界某些地區的郵遞區號是整數，但整數郵遞區號不應以模型中的數值資料表示。這是因為郵遞區號 20000 的效力並非 10000 郵遞區號的兩倍 (或一半)。此外，雖然不同郵遞區號確實與不同的房地產價值相關，但我們無法假設郵遞區號 20000 的房地產價值是郵遞區號 10000 的兩倍。郵遞區號應改為以類別資料表示。

數值特徵有時也稱為「連續特徵」。

詳情請參閱機器學習速成課程的「處理數值資料」。

O

離線

#fundamentals

static 的同義詞。

離線推論

#fundamentals

模型產生一批預測結果，然後快取 (儲存) 這些預測結果。應用程式接著可以從快取存取推斷的預測結果，而不必重新執行模型。

舉例來說，假設模型每四小時會產生一次當地天氣預報 (預測)。每次執行模型後，系統都會快取所有當地天氣預報。天氣應用程式會從快取擷取預報。

離線推論也稱為「靜態推論」。

與線上推論形成對比。 詳情請參閱機器學習速成課程中的「正式版機器學習系統：靜態與動態推論」。

one-hot 編碼

#fundamentals

將類別資料表示為向量，其中：

• 其中一個元素設為 1。
• 所有其他元素都會設為 0。

One-hot 編碼通常用於表示可能值有限的字串或 ID。舉例來說，假設名為 Scandinavia 的特定類別特徵有五個可能值：

• 「丹麥」
• 「瑞典」
• 「挪威」
• 「芬蘭」
• 「冰島」

One-hot 編碼可將這五個值分別表示如下：

國家/地區	向量
「丹麥」	1	0	0	0	0
「瑞典」	0	1	0	0	0
「挪威」	0	0	1	0	0
「芬蘭」	0	0	0	1	0
「冰島」	0	0	0	0	1

由於採用 one-hot 編碼，模型可以根據這五個國家/地區的資料，學習不同的連結。

將特徵表示為數值資料，是 one-hot 編碼的替代做法。很抱歉，以數字代表斯堪地那維亞國家/地區並非好選擇。舉例來說，請參考下列數字表示法：

• 「丹麥」為 0
• 「瑞典」為 1
• 「挪威」為 2
• 「芬蘭」是 3
• 「冰島」是 4

如果使用數值編碼，模型會以數學方式解讀原始數字，並嘗試根據這些數字進行訓練。然而，冰島的某項事物並非挪威的兩倍 (或一半)，因此模型會得出奇怪的結論。

詳情請參閱機器學習速成課程中的「類別資料：詞彙和獨熱編碼」。

一對多

#fundamentals

假設分類問題有 N 個類別，解決方案會包含 N 個獨立的二元分類模型，每個可能的結果都對應一個二元分類模型。舉例來說，假設模型會將樣本分類為動物、植物或礦物，一對多解決方案會提供下列三個獨立的二元分類模型：

• 動物與非動物
• 蔬菜與非蔬菜
• 礦物與非礦物

線上

#fundamentals

與 dynamic 語法相同。

線上推論

#fundamentals

依需求生成預測。舉例來說，假設應用程式將輸入內容傳遞至模型，並發出預測要求。使用線上推論的系統會執行模型，然後將預測結果傳回應用程式，以回應要求。

與離線推論形成對比。

詳情請參閱機器學習速成課程中的「正式版機器學習系統：靜態與動態推論」。

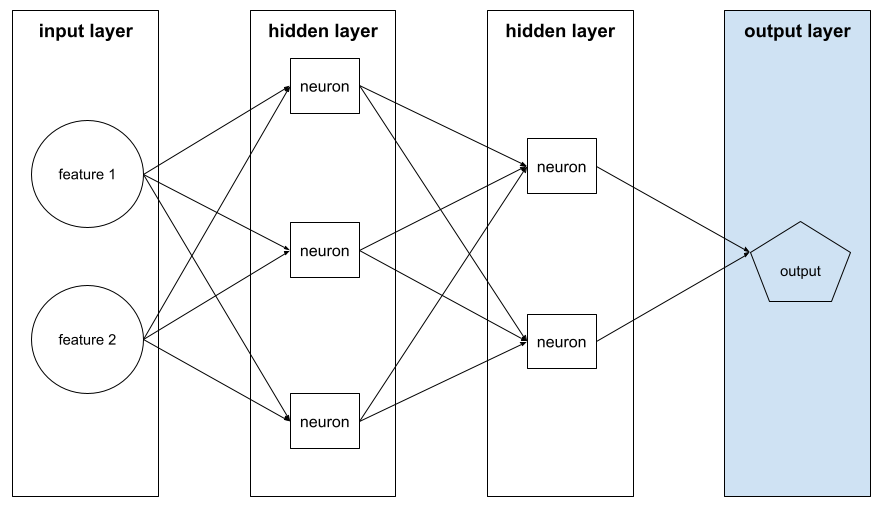
輸出層

#fundamentals

類神經網路的「最終」層。輸出層包含預測結果。

下圖顯示一個小型深層類神經網路，包含輸入層、兩個隱藏層和輸出層：

過度配適

#fundamentals

建立與訓練資料過於相符的模型，導致模型無法對新資料做出正確預測。

正規化可減少過度配適的情況。 使用大型且多元的訓練集進行訓練，也能減少過度配適。

按一下圖示即可查看其他附註。

過度擬合就像只嚴格遵循你最喜歡的老師的建議。您可能在該老師的課堂上表現優異，但可能會「過度配合」該老師的想法，而在其他課堂上表現不佳。聽取不同老師的建議，有助於你更妥善地適應新情況。

---

詳情請參閱機器學習速成課程中的「過度擬合」。

P

pandas

#fundamentals

以 numpy 為基礎建構的欄導向資料分析 API。 許多機器學習架構 (包括 TensorFlow) 都支援將 pandas 資料結構做為輸入內容。詳情請參閱 pandas 說明文件。

參數

#fundamentals

模型在訓練期間學到的權重和偏誤。舉例來說，在線性迴歸模型中，參數包含以下公式中的偏差 (b) 和所有權重 (w₁、w₂ 等等)：

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

相較之下，超參數是您 (或超參數微調服務) 提供給模型的值。舉例來說，學習率就是超參數。

正類

#fundamentals

#指標

您要測試的類別。

舉例來說，癌症模型中的正向類別可能是「腫瘤」。 電子郵件分類模型中的正類可能是「垃圾郵件」。

與負類形成對比。

按一下圖示即可查看其他附註。

「陽性類別」一詞可能會造成混淆，因為許多檢測的「陽性」結果通常是不良結果。舉例來說，許多醫療檢測中的陽性類別對應到腫瘤或疾病。一般來說，您會希望醫生告訴您「恭喜！您的檢測結果為陰性。」 無論如何，正向類別是測試要尋找的事件。

誠然，您同時測試正向和負向類別。

---

後續處理

#responsible

#fundamentals

在模型執行後調整輸出內容。 後續處理可用於強制執行公平性限制，而不需修改模型本身。

舉例來說，您可以設定分類門檻，對二元分類模型套用後續處理，確保某個屬性的機會均等，方法是檢查該屬性所有值的真正陽性率是否相同。

精確性

#fundamentals

#指標

分類模型的指標，可用來回答下列問題：

模型預測正類時，預測正確的百分比是多少？

公式如下：

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

其中：

• 真陽性是指模型正確預測正類。
• 偽陽性是指模型錯誤預測正類。

舉例來說，假設模型做出 200 項正向預測。在這 200 項正向預測中：

• 其中 150 個是真陽性。
• 其中 50 個是誤報。

在這種情況下：

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

與準確率和喚回度形成對比。

詳情請參閱機器學習速成課程中的「分類：準確度、喚回率、精確度和相關指標」。

預測

#fundamentals

模型的輸出內容。例如：

• 二元分類模型的預測結果不是正類就是負類。
• 多元分類模型會預測一個類別。
• 線性迴歸模型的預測結果是數字。

代理標籤

#fundamentals

資料集中沒有可直接使用的資料，因此無法估算標籤。

舉例來說，假設您必須訓練模型來預測員工壓力程度。您的資料集包含許多預測特徵，但沒有名為「壓力程度」的標籤。您不屈不撓，選擇「工作場所事故」做為壓力程度的替代標籤。畢竟，壓力大的員工比冷靜的員工更容易發生意外。還是會？或許工作場所事故的發生率會因為多種原因而起伏。

再舉一例，假設您想將「is it raining?」設為資料集的布林值標籤，但資料集不含降雨資料。如果有相片，您可以將「有人拿傘」的圖片設為「是否下雨？」的替代標籤。這是合適的代理標籤嗎？可能，但某些文化的人可能比較常帶傘來遮陽，而不是擋雨。

Proxy 標籤通常不盡完美。請盡可能選擇實際標籤，而非替代標籤。不過，如果沒有實際標籤，請非常謹慎地挑選替代標籤，選擇最不糟糕的替代標籤候選項目。

詳情請參閱機器學習速成課程中的「資料集：標籤」。

R

RAG

#fundamentals

檢索增強生成的縮寫。

評分者

#fundamentals

為範例提供標籤的人員。 「註解者」是評估者的另一個名稱。

詳情請參閱機器學習速成課程中的類別資料：常見問題。

召回

#fundamentals

#指標

分類模型的指標，可用來回答下列問題：

當基準真相為正類時，模型正確識別為正類的預測百分比是多少？

公式如下：

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

其中：

• 真陽性是指模型正確預測正類。
• 偽陰性表示模型錯誤預測為負類。

舉例來說，假設模型對基準真相為正類的樣本做出 200 項預測。在這 200 項預測中：

• 其中 180 個是真陽性。
• 其中 20 個是偽陰性。

在這種情況下：

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

按一下不平衡資料集相關附註的圖示。

如果分類模型中正類別很少見，則召回率特別有助於判斷模型的預測能力。舉例來說，假設有類別不平衡的資料集，其中某種疾病的正類只出現在一百萬名患者中的 10 位。假設您的模型進行了五百萬次預測，並產生下列結果：

• 30 個真陽性
• 20 個偽陰性
• 4,999,000 個真陰性
• 950 個誤報

因此，這個模型的喚回率為：

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

相較之下，這個模型的準確率為：

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

高準確率看起來很厲害，但其實沒有意義。 對於類別不平衡的資料集，喚回度比準確度更有用。

---

詳情請參閱「分類：準確度、查全率、查準率和相關指標」。

線性整流函數 (ReLU)

#fundamentals

具有下列行為的啟動函式：

• 如果輸入值為負數或零，輸出值則為 0。
• 如果輸入為正數，輸出會等於輸入。

例如：

• 如果輸入內容為 -3，則輸出內容為 0。
• 如果輸入為 +3，則輸出為 3.0。

以下是 ReLU 的繪圖：

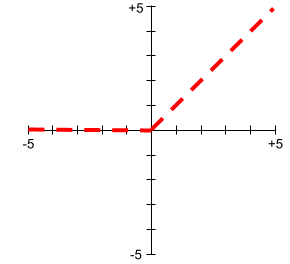
ReLU 是非常熱門的活化函式。雖然 ReLU 的行為很簡單，但仍可讓類神經網路學習非線性的特徵與標籤之間的關係。

迴歸模型

#fundamentals

簡單來說，迴歸模型會產生數值預測結果。(相較之下，分類模型會產生類別預測結果)。舉例來說，下列都是迴歸模型：

• 預測特定房屋價值 (以歐元計) 的模型，例如 423,000。
• 模型會預測特定樹木的壽命 (以年為單位)，例如 23.2 年。
• 預測未來六小時內某個城市降雨量 (以英吋為單位) 的模型，例如 0.18。

迴歸模型有兩種常見類型：

• 線性迴歸：找出最符合特徵標籤值的線。
• 邏輯迴歸：產生介於 0.0 和 1.0 之間的機率，系統通常會將此機率對應至類別預測。

並非所有輸出數值預測結果的模型都是迴歸模型。 在某些情況下，數值預測實際上只是類別名稱為數值的分類模型。舉例來說，預測數字郵遞區號的模型是分類模型，而非迴歸模型。

正則化

#fundamentals

任何可減少過度擬合的機制。 常見的正規化類型包括：

• L₁ 正規化
• L₂ 正規化
• 丟棄正則化
• 提早停止 (這不是正式的正規化方法，但可以有效限制過度擬合)

正規化也可以定義為模型複雜度的懲罰。

按一下圖示即可查看其他附註。

正則化與直覺相反。增加正則化通常會增加訓練損失，這令人困惑，因為目標不是要盡量減少訓練損失嗎？

其實不然，目標並非盡量減少訓練損失，目標是針對實際範例做出準確預測。值得注意的是，即使增加正則化會增加訓練損失，但通常有助於模型對實際範例做出更準確的預測。

---

詳情請參閱機器學習速成課程中的「過度擬合：模型複雜度」。

正規化率

#fundamentals

這個數字會指定訓練期間正規化的相對重要性。提高正規化率可減少過度配適，但可能會降低模型的預測能力。反之，降低或省略正規化率會增加過度擬合。

按一下圖示即可查看數學式。

正規化率通常以希臘字母 lambda 表示。下列簡化版損失方程式顯示 lambda 的影響：

$$\text{minimize(loss function + }\lambda\text{(regularization))}$$

其中「regularization」是任何正規化機制，包括：

• L₁ 正規化
• L₂ 正規化

---

詳情請參閱機器學習速成課程中的「過度擬合：L2 正規化」。

ReLU

#fundamentals

線性整流函數的縮寫。

檢索增強生成 (RAG)

#fundamentals

這項技術可利用模型訓練後檢索到的知識來源建立基準，增進大型語言模型 (LLM) 輸出內容的品質。RAG 可讓經過訓練的 LLM 存取從可信知識庫或文件擷取的資訊，藉此提升 LLM 回覆的準確度。

使用檢索增強生成技術的常見動機包括：

• 提高模型生成回覆的事實準確度。
• 讓模型存取未經訓練的知識。
• 變更模型使用的知識。
• 讓模型引用來源。

舉例來說，假設化學應用程式使用 PaLM API 產生與使用者查詢相關的摘要。應用程式後端收到查詢時，後端會執行下列操作：

1. 搜尋 (「擷取」) 與使用者查詢相關的資料。
2. 在使用者查詢中附加 (「擴增」) 相關化學資料。
3. 指示 LLM 根據附加資料建立摘要。

ROC 曲線

#fundamentals

#指標

二元分類中，不同分類閾值的真陽率與偽陽率圖表。

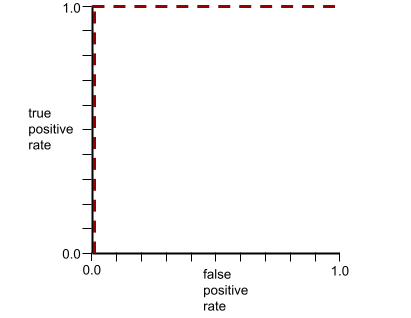
ROC 曲線的形狀代表二元分類模型區分正類和負類的能力。舉例來說，假設二元分類模型完美區分了所有負類和正類：

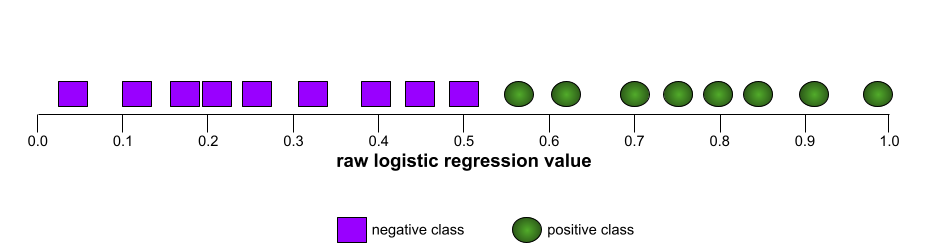
上述模型的 ROC 曲線如下所示：

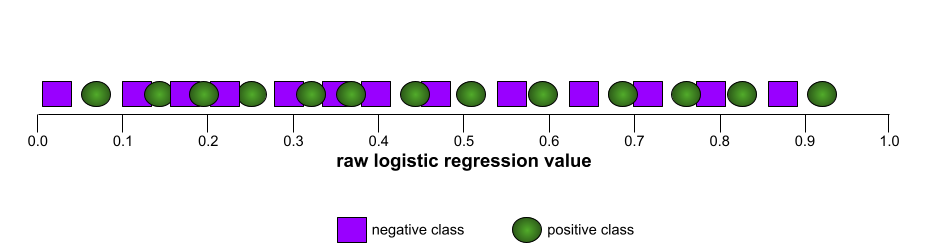
相較之下，下圖繪製了原始邏輯迴歸值，代表模型效能不佳，完全無法區分負面類別和正面類別：

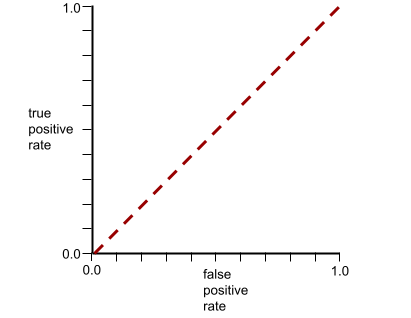
這個模型的 ROC 曲線如下所示：

同時，在現實世界中，大多數二元分類模型都會在某種程度上區分正類和負類，但通常不會完美區分。因此，典型的 ROC 曲線會落在兩個極端之間：

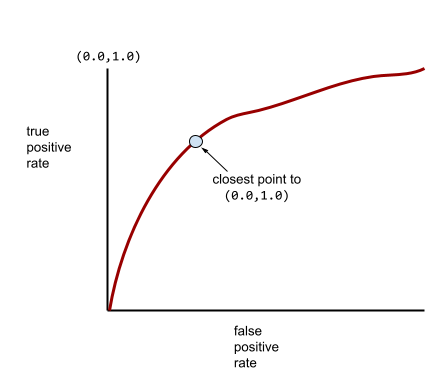
ROC 曲線最接近 (0.0,1.0) 的點，理論上會找出理想的分類門檻。不過，其他幾個現實世界的問題會影響理想分類門檻的選取。舉例來說，偽陰性造成的困擾可能遠大於偽陽性。

AUC 是用來彙整 ROC 曲線的數值指標，會以單一浮點數值表示。

均方根誤差 (RMSE)

#fundamentals

#指標

均方誤差的平方根。

日

S 函數

#fundamentals

這個數學函式會將輸入值「擠壓」到受限範圍內，通常是 0 到 1 或 -1 到 +1。也就是說，您可以將任何數字 (2、100 萬、負 10 億等) 傳遞至 Sigmoid 函數，輸出結果仍會落在受限範圍內。Sigmoid 啟動函式的繪圖如下所示：

機器學習中有多種用途，包括：

• 將邏輯迴歸或多項式迴歸模型的原始輸出內容轉換為機率。
• 在某些類神經網路中，做為啟動函式。

按一下圖示即可查看數學式。

輸入數字 x 的 Sigmoid 函式公式如下：

$$ sigmoid(x) = \frac{1}{1 + e^{-\text{x}}} $$

在機器學習中，x 通常是加權總和。

---

softmax

#fundamentals

這個函式會判斷多元分類模型中每個可能類別的機率。機率總和必須為 1.0。舉例來說，下表顯示 Softmax 如何分配各種機率：

圖片為...	機率
狗	.85
cat	.13
馬	.02

Softmax 也稱為「完整 softmax」。

與候選抽樣形成對比。

按一下圖示即可查看數學式。

Softmax 方程式如下：

$$\sigma_i = \frac{e^{\text{z}_i}} {\sum_{j=1}^{j=K} {e^{\text{z}_j}}} $$

其中：

• $\sigma_i$ 是輸出向量。輸出向量的每個元素都會指定這個元素的機率。輸出向量中所有元素的總和為 1.0。輸出向量包含的元素數量與輸入向量 $z$ 相同。
• $z$ 是輸入向量。輸入向量的每個元素都包含浮點值。
• $K$ 是輸入向量 (和輸出向量) 中的元素數量。

舉例來說，假設輸入向量為：

[1.2, 2.5, 1.8]

因此，softmax 會以下列方式計算分母：

$$\text{denominator} = e^{1.2} + e^{2.5} + e^{1.8} = 21.552$$

因此，每個元素的 Softmax 機率為：

$$\sigma_1 = \frac{e^{1.2}}{21.552} = 0.154 $$ $$\sigma_2 = \frac{e^{2.5}}{21.552} = 0.565 $$ $$\sigma_1 = \frac{e^{1.8}}{21.552} = 0.281 $$

因此，輸出向量為：

$$\sigma = [0.154, 0.565, 0.281]$$

$\sigma$ 中三個元素的總和為 1.0。呼！

---

詳情請參閱機器學習速成課程中的「類神經網路：多類別分類」。

稀疏特徵

#fundamentals

值大多為零或空白的特徵。舉例來說，如果特徵包含單一 1 值和一百萬個 0 值，就是稀疏特徵。相反地，密集特徵的值大多不是零或空白。

在機器學習中，有許多特徵都是稀疏特徵。類別特徵通常是稀疏特徵。 舉例來說，如果森林中有 300 種可能的樹木，單一範例可能只會識別出楓樹。或者，在影片庫中數百萬部可能的影片中，單一範例可能只會識別出「北非諜影」。

在模型中，您通常會使用 one-hot 編碼表示稀疏特徵。如果 one-hot 編碼很大，您可能會在 one-hot 編碼的頂端放置嵌入層，以提高效率。

稀疏表示法

#fundamentals

只儲存稀疏特徵中非零元素的位置。

舉例來說，假設名為 species 的類別特徵可識別特定森林中的 36 種樹木。進一步假設每個範例只會識別單一物種。

您可以使用單熱向量表示每個範例中的樹種。獨熱向量會包含單一 1 (代表該範例中的特定樹種) 和 35 個 0 (代表該範例中不屬於該樹種的 35 個樹種)。因此，maple 的 one-hot 表示法可能如下所示：

或者，稀疏表示法只會識別特定物種的位置。如果 maple 位於位置 24，則 maple 的稀疏表示法會是：

24

請注意，稀疏表示法比 one-hot 表示法精簡許多。

注意： 請勿將稀疏表示法做為模型的直接特徵輸入內容傳遞。建議先將稀疏表示法轉換為 one-hot 表示法，再進行訓練。

按一下圖示，查看稍微複雜的範例。

假設模型中的每個範例都必須代表英文句子中的字詞，但不能代表這些字詞的順序。英文約有 17 萬個字，因此英文是類別特徵，約有 17 萬個元素。大多數英文句子只會用到這 17 萬個字詞中極少的部分，因此單一範例中的字詞集幾乎肯定會是稀疏資料。

請參考以下句子：

My dog is a great dog

您可以使用單熱向量的變體來表示這個句子中的字詞。在這個變體中，向量中的多個儲存格可以包含非零值。此外，在這個變體中，儲存格可以包含非一的整數。雖然「my」、「is」、「a」和「great」這些字詞在句子中只出現一次，但「dog」這個字詞出現了兩次。使用這個單熱向量變體來表示這個句子中的字詞，會產生下列 170,000 個元素的向量：

同一句的稀疏表示法如下：

0: 1
26100: 2
45770: 1
58906: 1
91520: 1

---

如有任何疑問，請按一下該圖示。

「稀疏表示法」一詞會讓許多人感到困惑，因為稀疏表示法本身並非稀疏向量。稀疏表示法實際上是稀疏向量的密集表示法。同義字索引表示法比「稀疏表示法」清楚一點。

---

詳情請參閱機器學習速成課程中的「使用類別型資料」。

稀疏向量

#fundamentals

向量的值大多為零。另請參閱「稀疏特徵」和「稀疏性」。

平方損失

#fundamentals

#指標

L₂ 損失 的同義詞。

靜態

#fundamentals

一次性作業，而非持續性作業。 「靜態」和「離線」是同義詞。 以下是機器學習中 static 和 offline 的常見用途：

• 靜態模型 (或離線模型) 是指訓練一次後，可使用一段時間的模型。
• 靜態訓練 (或離線訓練) 是指訓練靜態模型的過程。
• 靜態推論 (或離線推論) 是指模型一次生成一批預測結果的程序。

與動態對比。

靜態推論

#fundamentals

離線推論的同義詞。

平穩性

#fundamentals

值不會在一或多個維度 (通常是時間) 之間變更的特徵。舉例來說，如果特徵在 2021 年和 2023 年的值大致相同，就表示該特徵具有平穩性。

在現實世界中，很少有特徵呈現平穩性。即使是與穩定性同義的特徵 (例如海平面)，也會隨時間變化。

與非平穩性形成對比。

隨機梯度下降 (SGD)

#fundamentals

梯度下降演算法，其中批次大小為 1。換句話說，SGD 會從訓練集中隨機選擇一個範例進行訓練。

詳情請參閱機器學習速成課程中的「線性迴歸：超參數」。

監督式機器學習

#fundamentals

從特徵和對應的標籤訓練模型。監督式機器學習類似於學習某個科目時，研究一組問題及其對應的答案。掌握問題與答案之間的對應關係後，學生就能回答同一主題的新問題 (從未見過的問題)。

與非監督式機器學習比較。

詳情請參閱「機器學習簡介」課程中的「監督式學習」。

合成特徵

#fundamentals

特徵並未出現在輸入特徵中，但由一或多個輸入特徵組合而成。建立合成特徵的方法包括：

• 分組：將連續特徵分組到範圍值區。
• 建立特徵交集。
• 將一個特徵值乘以 (或除以) 其他特徵值或本身。舉例來說，如果 a 和 b 是輸入特徵，則下列為合成特徵的範例：
  • ab
  • a²
• 將超越函數套用至特徵值。舉例來說，如果 c 是輸入特徵，則下列為合成特徵的範例：
  • sin(c)
  • ln(c)

單獨透過正規化或縮放建立的特徵不算是合成特徵。

T

測試損失

#fundamentals

#指標

代表模型對測試集的損失的指標。建構模型時，您通常會盡量減少測試損失。這是因為相較於低訓練損失或低驗證損失，低測試損失是更強大的品質信號。

如果測試損失與訓練損失或驗證損失之間存在巨大差距，有時表示您需要提高正規化率。

訓練

#fundamentals

決定構成模型的理想參數 (權重和偏差) 的過程。在訓練期間，系統會讀取範例，並逐步調整參數。訓練會使用每個範例幾次到數十億次。

詳情請參閱「機器學習簡介」課程中的「監督式學習」。

訓練損失

#fundamentals

#指標

代表模型在特定訓練疊代期間的損失指標。舉例來說，假設損失函式為平均平方誤差。舉例來說，第 10 次疊代的訓練損失 (均方誤差) 為 2.2，第 100 次疊代的訓練損失為 1.9。

損失曲線會繪製訓練損失與疊代次數的關係圖。損失曲線可提供下列訓練提示：

• 如果斜率向下，表示模型正在進步。
• 如果斜率向上，表示模型品質正在變差。
• 平緩的斜率表示模型已達到收斂。

舉例來說，以下是經過某種程度理想化的損失曲線，顯示：

• 在初期反覆執行階段，斜率大幅下降，表示模型快速進步。
• 斜率逐漸趨緩 (但仍向下)，直到訓練接近尾聲為止，這表示模型持續進步，但速度比初期反覆運算時稍慢。
• 訓練結束時的斜率平緩，表示模型已收斂。

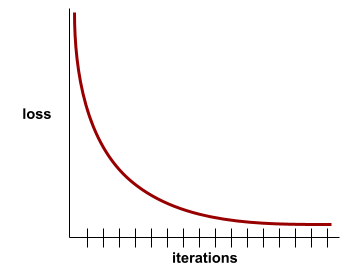
雖然訓練損失很重要，但請參閱泛化。

訓練/應用偏差

#fundamentals

模型在訓練期間的效能，與該模型在服務期間的效能差異。

訓練集

#fundamentals

用於訓練模型的資料集子集。

傳統上，資料集中的樣本會分成下列三個不同的子集：

• 訓練集
• 驗證集
• 測試集

理想情況下，資料集中的每個樣本都應只屬於上述其中一個子集。舉例來說，單一範例不應同時屬於訓練集和驗證集。

詳情請參閱機器學習速成課程中的「資料集：分割原始資料集」。

真陰性 (TN)

#fundamentals

#指標

舉例來說，模型正確預測負類。舉例來說，模型推斷某封電子郵件不是垃圾郵件，而該電子郵件確實不是垃圾郵件。

真陽性 (TP)

#fundamentals

#指標

舉例來說，模型正確預測正類。舉例來說，模型推斷特定電子郵件是垃圾郵件，而該電子郵件確實是垃圾郵件。

真陽率 (TPR)

#fundamentals

#指標

recall 的同義詞。也就是：

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

真陽率是 ROC 曲線的 y 軸。

U

配適不足

#fundamentals

模型未能充分掌握訓練資料的複雜度，導致模型的預測能力不佳。許多問題都可能導致欠擬合，包括：

• 以錯誤的特徵集進行訓練。
• 訓練的週期太少，或學習率太低。
• 訓練時正規化率過高。
• 在深層類神經網路中提供的隱藏層太少。

詳情請參閱機器學習速成課程中的「過度擬合」。

無標籤樣本

#fundamentals

包含特徵，但不含標籤的範例。 舉例來說，下表顯示房屋估價模型中的三個未標記範例，每個範例都有三項特徵，但沒有房屋價值：

臥室數量	浴室數量	房屋屋齡
3	2	15
2	1	72
4	2	34

在監督式機器學習中，模型會根據加上標籤的樣本進行訓練，並對未加上標籤的樣本做出預測。

在半監督式和非監督式學習中，訓練期間會使用未標記的範例。

對比無標籤樣本與有標籤樣本。

非監督式機器學習

#clustering

#fundamentals

訓練模型，找出資料集中的模式，通常是未標記的資料集。

非監督式機器學習最常見的用途是將資料分群，分成類似範例的群組。舉例來說，非監督式機器學習演算法可以根據音樂的各種屬性，將歌曲分群。產生的叢集可做為其他機器學習演算法的輸入內容 (例如音樂推薦服務)。如果實用標籤很少或沒有，分群功能就很有幫助。 舉例來說，在反濫用和詐欺等領域，叢集可協助人類進一步瞭解資料。

與監督式機器學習形成對比。

按一下圖示即可查看其他附註。

非監督式機器學習的另一個例子是主成分分析 (PCA)。舉例來說，對含有數百萬個購物車內容的資料集套用 PCA，可能會發現含有檸檬的購物車通常也含有制酸劑。

---

詳情請參閱「機器學習簡介」課程中的「什麼是機器學習？」一節。

V

驗證

#fundamentals

模型的初步品質評估。驗證會根據驗證集檢查模型預測的品質。

由於驗證集與訓練集不同，因此驗證有助於防範過度配適。

您可以將針對驗證集評估模型視為第一輪測試，而針對測試集評估模型則視為第二輪測試。

驗證損失

#fundamentals

#指標

代表模型在特定訓練疊代期間，於驗證集上的損失指標。

另請參閱一般化曲線。

驗證集

#fundamentals

資料集的子集，用於針對已訓練的模型執行初步評估。通常您會先針對驗證集多次評估訓練好的模型，再針對測試集評估模型。

傳統上，您會將資料集中的範例分成下列三個不同的子集：

• 訓練集
• 驗證集
• 測試集

理想情況下，資料集中的每個樣本都應只屬於上述其中一個子集。舉例來說，單一範例不應同時屬於訓練集和驗證集。

詳情請參閱機器學習速成課程中的「資料集：分割原始資料集」。

W

重量

#fundamentals

模型要與另一個值相乘的值。訓練是決定模型理想權重的程序；推論則是使用這些學到的權重進行預測的程序。

按一下圖示，查看線性模型中的權重範例。

假設有兩個特徵的線性模型。假設訓練作業決定了下列權重 (和偏差)：

• 偏誤 b 的值為 2.2
• 與一項特徵相關聯的權重 w₁ 為 1.5。
• 與其他特徵相關聯的權重 w₂ 為 0.4。

現在假設有範例，其特徵值如下：

• 其中一個特徵的值 x₁ 為 6。
• 另一個特徵 x₂ 的值為 10。

這個線性模型會使用下列公式產生預測值 y'：

$$y' = b + w_1x_1 + w_2x_2$$

因此預測結果為：

$$y' = 2.2 + (1.5)(6) + (0.4)(10) = 15.2$$

如果權重為 0，對應的特徵就不會對模型做出貢獻。舉例來說，如果 w₁ 為 0，則 x₁ 的值無關緊要。

---

詳情請參閱機器學習速成課程中的線性迴歸。

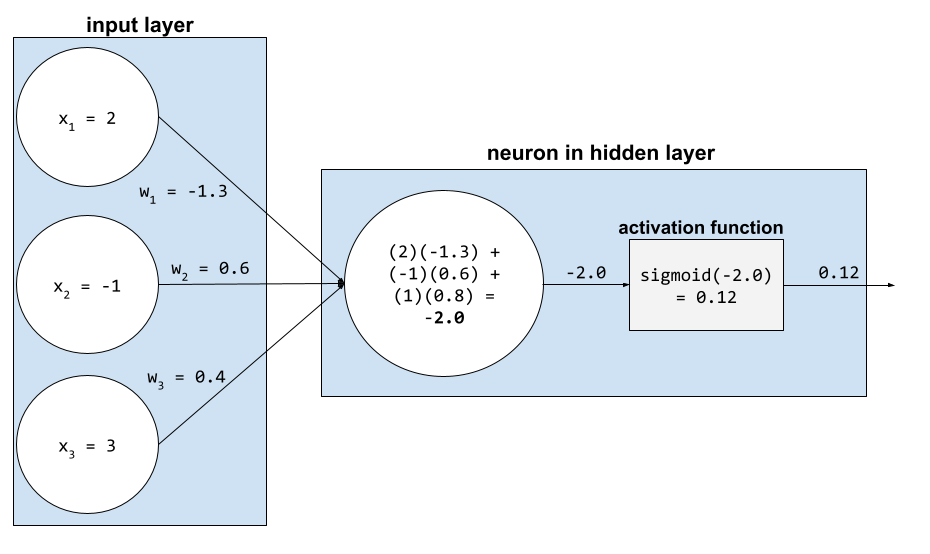
加權總和

#fundamentals

所有相關輸入值乘以對應權重的總和。舉例來說，假設相關輸入內容如下：

輸入值	輸入重量
2	-1.3
-1	0.6
3	0.4

因此加權後的總和為：

weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0

加權總和是啟動函式的輸入引數。

Z

標準分數正規化

#fundamentals

一種縮放技術，可將原始特徵值替換為浮點值，代表該特徵與平均值的標準差數。舉例來說，假設某項特徵的平均值為 800，標準差為 100。下表顯示 Z 分數常態化如何將原始值對應至 Z 分數：

原始值	標準分數
800	0
950	+1.5
575	-2.25

接著，機器學習模型會根據該特徵的 Z 分數進行訓練，而不是原始值。

詳情請參閱機器學習速成課程中的「數值資料：正規化」。