本節將探討下列三個問題:
- 類別平衡資料集和類別不平衡資料集有何不同?
- 為什麼訓練不平衡資料集很困難?
- 如何克服訓練不平衡資料集的問題?
類別平衡資料集與類別不平衡資料集
假設資料集包含類別標籤,其值為正向類別或負向類別。在類別平衡資料集中,正向類別和負向類別的數量大致相等。舉例來說,如果資料集包含 235 個正向類別和 247 個負向類別,就是平衡的資料集。
在不平衡資料集中,某個標籤的出現頻率遠高於其他標籤。在現實世界中,不平衡資料集遠比平衡資料集常見。舉例來說,在信用卡交易資料集中,詐欺購物可能只占不到 0.1% 的樣本。同樣地,在醫療診斷資料集中,感染罕見病毒的病患人數可能不到總樣本的 0.01%。在不平衡資料集中:
訓練嚴重類別不平衡資料集的困難
訓練的目的是建立模型,成功區分正類和負類。如要這麼做,批次需要足夠數量的正向和負向類別。如果訓練資料集中的類別不平衡程度較輕微,這就不成問題,因為即使是小批次,通常也會包含足夠的正向和負向類別範例。不過,如果資料集嚴重類別不平衡,可能就沒有足夠的少數類別範例可供適當訓練。
舉例來說,請看圖 6 所示的不平衡資料集,其中:
- 200 個標籤屬於多數類別。
- 2 個標籤屬於少數類別。
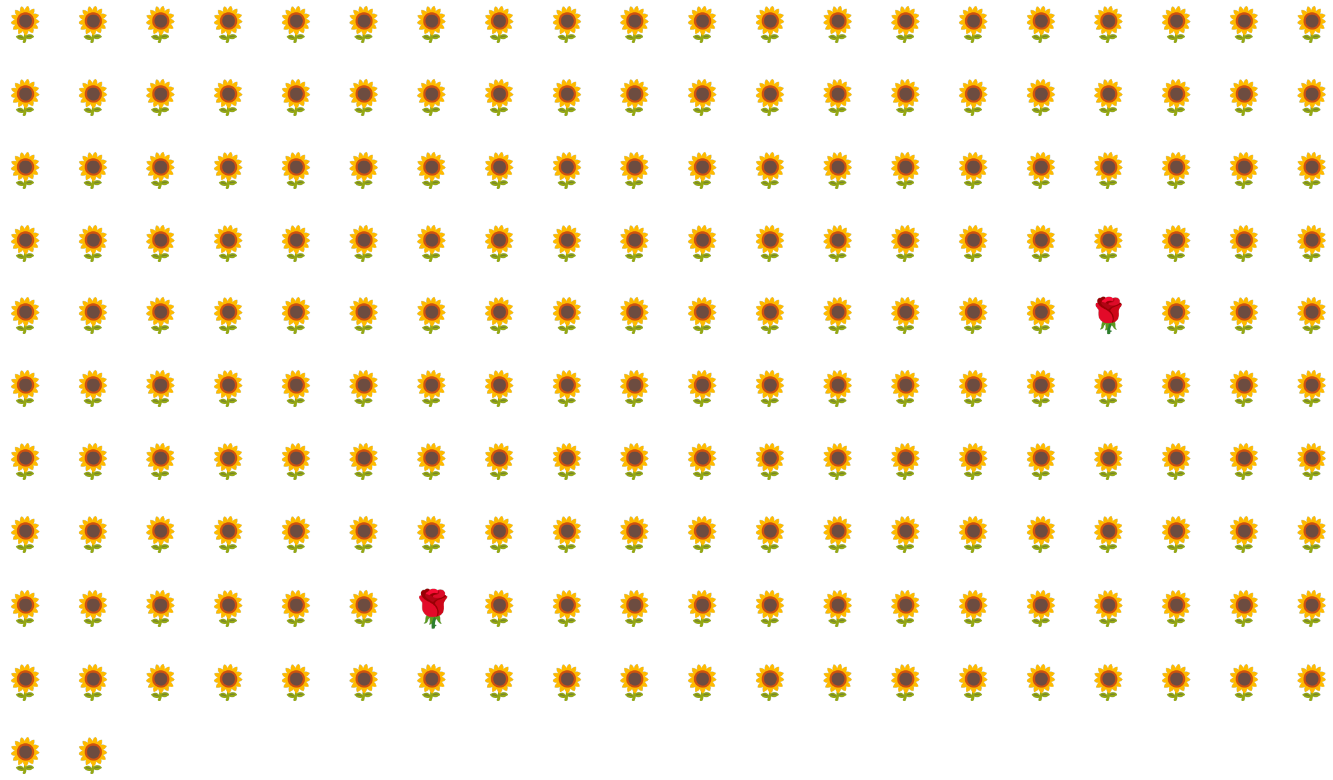
如果批次大小為 20,大多數批次都不會包含任何少數類別的樣本。如果批次大小為 100,則每個批次平均只會包含一個少數類別範例,這不足以進行適當的訓練。即使批次大小大得多,仍會產生如此不平衡的比例,模型可能無法正常訓練。
訓練不平衡資料集
在訓練期間,模型應學習兩件事:
- 每個類別的樣貌,也就是哪些特徵值對應至哪些類別?
- 每個類別的常見程度,也就是類別的相對分布情況。
標準訓練會混淆這兩項目標。相較之下,下列兩步驟技術 (稱為多數類別的下採樣和加權) 會區分這兩項目標,讓模型同時達成這兩項目標。
步驟 1:對多數類別進行下採樣
欠採樣是指以比例極低的少數類別樣本進行訓練。也就是說,您會從訓練資料中省略許多多數類別的範例,人為地強制讓不平衡的資料集變得較為平衡。降採樣可大幅提高每個批次包含足夠少數類別範例的機率,進而適當且有效率地訓練模型。
舉例來說,圖 6 所示的類別不平衡資料集包含 99% 的多數類別和 1% 的少數類別範例。將多數類別的樣本數減少 25 倍,人為建立更平衡的訓練集 (多數類別占 80%,少數類別占 20%),如圖 7 所示:

步驟 2:提高下採樣類別的權重
下取樣會向模型展示類別比現實世界更平衡的人工世界,進而造成預測偏差。如要修正這項偏差,您必須將多數類別「加權」,加權因數為您進行向下取樣的因數。加權表示對多數類別範例的損失,比對少數類別範例的損失更嚴厲。
舉例來說,我們將多數類別的樣本數減少 25 倍,因此必須將多數類別的權重增加 25 倍。也就是說,如果模型錯誤預測多數類別,請將損失視為 25 個錯誤 (將一般損失乘以 25)。

您應該減少取樣多少資料,並增加多少權重,才能重新平衡資料集?如要找出答案,您應嘗試不同的下取樣和加權因子,就像嘗試其他超參數一樣。
這項技術的優點
對多數類別進行向下取樣並提高權重,可帶來下列優點:
- 更優質的模型:產生的模型「知道」以下兩件事:
- 特徵與標籤之間的關聯
- 類別的實際分布情形
- 加快收斂速度:在訓練期間,模型會更常看到少數類別,有助於加快收斂速度。
