超參數是可控制訓練各個層面的變數。三種常見的超參數如下:
相反地,參數是模型本身的變數,例如權重和偏差。換句話說,超參數是您控制的值,而參數是模型在訓練期間計算的值。
學習率
學習率是您設定的浮點數,會影響模型收斂的速度。如果學習率過低,模型可能需要很長時間才能收斂。不過,如果學習率過高,模型就永遠不會收斂,而是會在可將損失降至最低的權重和偏差值之間跳動。目標是選擇適中的學習率,讓模型快速收斂。
學習率會決定梯度下降過程的每個步驟中,權重和偏差的變化幅度。模型會將梯度乘以學習率,藉此決定下一次疊代的模型參數 (權重和偏差值)。在梯度下降的第三個步驟中,朝負斜率方向移動的「少量」是指學習率。
舊模型參數和新模型參數之間的差異與損失函式的斜率成正比。舉例來說,如果斜率較大,模型就會採取較大的步距。如果很小,則會小幅移動。舉例來說,如果梯度大小為 2.5,學習率為 0.01,模型就會將參數變更 0.025。
理想的學習率可協助模型在合理次數的疊代中收斂。如圖 20 所示,損失曲線顯示模型在前 20 次疊代期間大幅改善,之後開始收斂:
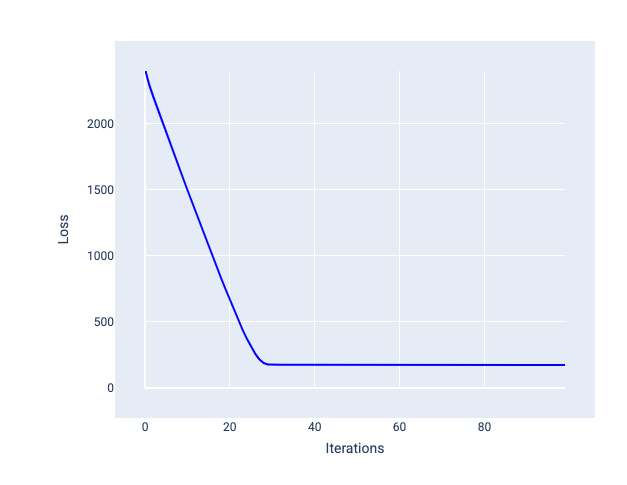
圖 20. 損失圖表:顯示以快速收斂的學習率訓練的模型。
相反地,如果學習率過低,可能需要多次疊代才能收斂。如圖 21 所示,損失曲線顯示模型在每次疊代後只會進行小幅改良:
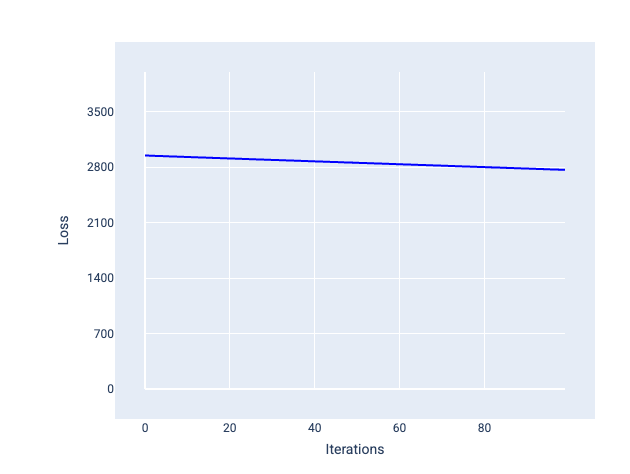
圖 21. 損失圖表:以低學習率訓練的模型。
學習率過高時,每次疊代都會導致損失值不斷跳動或持續增加,因此永遠不會收斂。在圖 22 中,損失曲線顯示模型在每次疊代後損失減少,然後增加損失,而在圖 23 中,損失在後續疊代中增加:
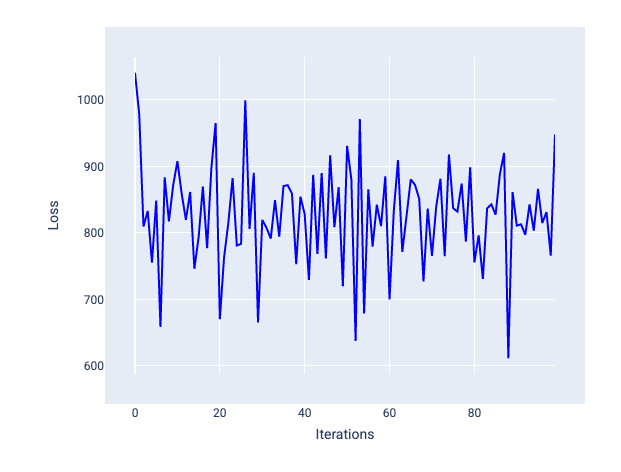
圖 22. 損失圖表:顯示以過大學習率訓練的模型,損失曲線會隨著疊代次數增加而大幅波動。
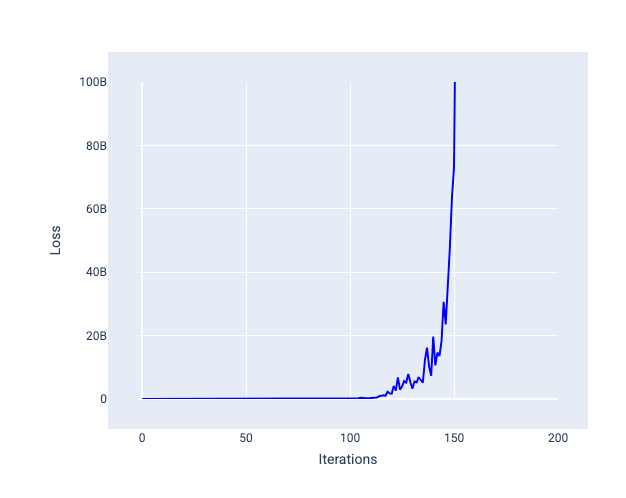
圖 23. 損失圖表:模型訓練時的學習率過高,導致損失曲線在後續疊代中大幅增加。
練習:確認您的理解程度
批量
批次大小是超參數,指的是模型在更新權重和偏差前處理的範例數量。您可能會認為模型應先計算資料集中每個樣本的損失,再更新權重和偏差。不過,如果資料集包含數十萬甚至數百萬個樣本,使用完整批次並不實際。
如要取得平均梯度,而不必在更新權重和偏差前查看資料集中的每個範例,有兩種常見的技術:隨機梯度下降和迷你批次隨機梯度下降:
隨機梯度下降 (SGD):隨機梯度下降在每次疊代時只會使用單一範例 (批次大小為 1)。只要有足夠的疊代次數,SGD 就能運作,但會產生大量雜訊。「雜訊」是指訓練期間的變異,導致疊代期間的損失增加而非減少。「隨機」一詞表示每個批次中的一個範例是隨機選擇。
請注意下圖,模型使用 SGD 更新權重和偏差時,損失會稍微波動,這可能會導致損失圖表出現雜訊:
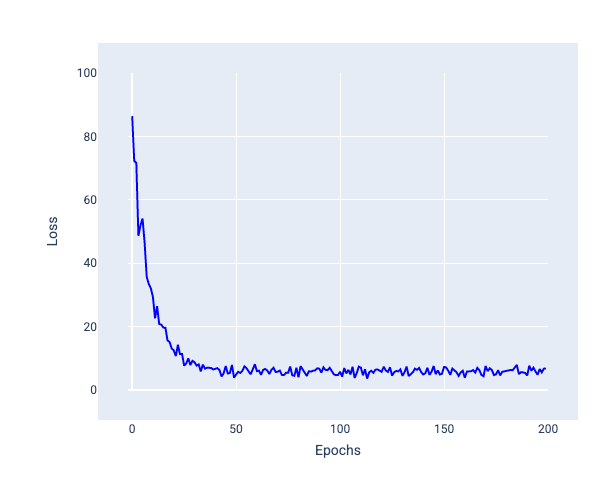
圖 24. 以隨機梯度下降 (SGD) 訓練的模型,損失曲線中出現雜訊。
請注意,使用隨機梯度下降法可能會在整個損失曲線中產生雜訊,而不僅是在收斂附近。
小批隨機梯度下降法 (小批 SGD):小批隨機梯度下降法是全批和 SGD 之間的折衷方案。如果資料點數量為 $ N $,批次大小可以是任何大於 1 且小於 $ N $ 的數字。模型會隨機選擇每個批次中包含的樣本,計算這些樣本的梯度平均值,然後在每次疊代時更新權重和偏差。
每個批次的範例數量取決於資料集和可用的運算資源。一般來說,小批量大小的行為類似於 SGD,而大批量大小的行為類似於全批量梯度下降。
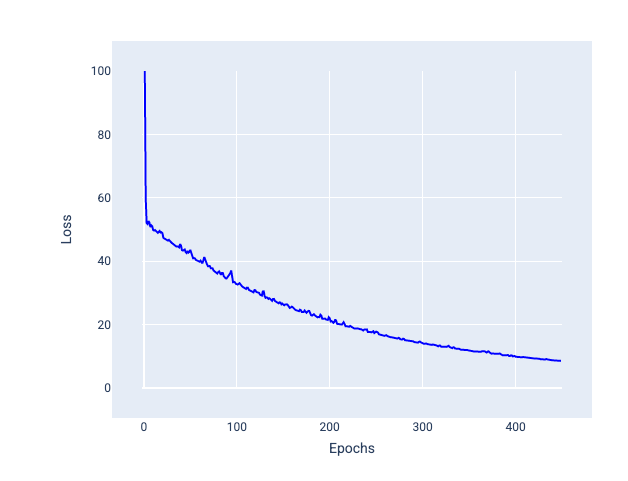
圖 25. 使用小批隨機梯度下降法訓練的模型。
訓練模型時,您可能會認為雜訊是不良特徵,應該要消除。不過,適量的干擾可能是有益的。在後續單元中,您將瞭解雜訊如何協助模型更妥善地泛化,並在神經網路中找出最佳權重和偏差。
訓練週期數量
在訓練期間,一個訓練週期表示模型已一次處理訓練集中的每個範例。舉例來說,如果訓練集有 1,000 個樣本,而迷你批次大小為 100 個樣本,模型需要 10 次疊代才能完成一個訓練週期。
訓練通常需要許多訓練週期。也就是說,系統需要多次處理訓練集中的每個範例。
訓練週期數是您在模型開始訓練前設定的超參數。在許多情況下,您需要實驗模型收斂所需的訓練週期數。一般來說,訓練週期越多,模型越好,但訓練時間也越長。
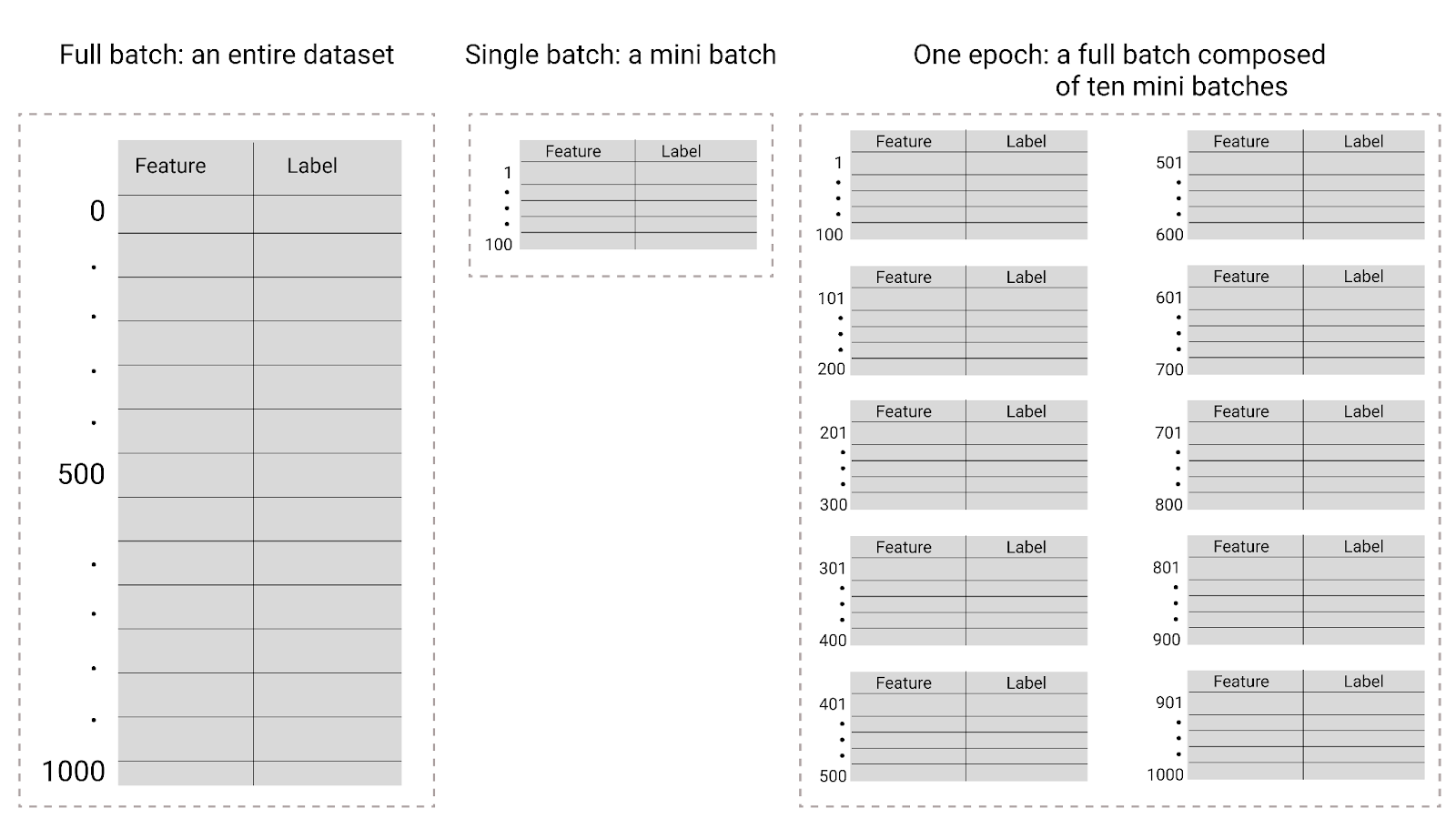
圖 26. 完整批次與迷你批次。
下表說明批次大小和訓練週期與模型更新參數次數的關係。
| 批次類型 | 權重和偏誤更新時 |
|---|---|
| 完整批次 | 模型查看資料集中的所有範例後,舉例來說,如果資料集包含 1,000 個範例,且模型訓練 20 個訓練週期,模型就會更新權重和偏差 20 次,每個訓練週期更新一次。 |
| 隨機梯度下降 | 模型查看資料集中的單一範例後。舉例來說,如果資料集包含 1,000 個範例,且訓練 20 個週期,模型就會更新權重和偏差 20,000 次。 |
| 小批隨機梯度下降法 | 模型會先查看每個批次中的範例,舉例來說,如果資料集包含 1,000 個樣本,批次大小為 100,且模型訓練 20 個週期,模型就會更新權重和偏差 200 次。 |
