Ten glosariusz zawiera definicje terminów związanych z uczeniem maszynowym.
A
ablacja
Technika oceny ważności cechy lub komponentu przez tymczasowe usunięcie go z modelu. Następnie ponownie trenujesz model bez tej funkcji lub komponentu. Jeśli po ponownym wytrenowaniu model działa znacznie gorzej, usunięta funkcja lub komponent prawdopodobnie były ważne.
Załóżmy na przykład, że trenujesz model klasyfikacji na podstawie 10 cech i uzyskujesz 88% precyzji w zbiorze testowym. Aby sprawdzić znaczenie pierwszej cechy, możesz ponownie wytrenować model, używając tylko 9 pozostałych cech. Jeśli ponownie wytrenowany model działa znacznie gorzej (np. ma precyzję poniżej 55%), usunięta cecha była prawdopodobnie ważna. Z kolei jeśli po ponownym wytrenowaniu model działa równie dobrze, to prawdopodobnie ta cecha nie była aż tak ważna.
Ablacja może też pomóc określić znaczenie:
- większe komponenty, np. cały podsystem większego systemu uczenia maszynowego;
- procesy lub techniki, takie jak krok wstępnego przetwarzania danych;
W obu przypadkach możesz obserwować, jak zmienia się (lub nie zmienia) skuteczność systemu po usunięciu komponentu.
Testy A/B
Statystyczna metoda porównywania co najmniej 2 technik – A i B. Zazwyczaj A to dotychczasowa technika, a B to nowa technika. Testy A/B nie tylko pozwalają określić, która technika jest skuteczniejsza, ale też czy różnica jest istotna statystycznie.
Test A/B zwykle porównuje 1 rodzaj danych w przypadku 2 technik. Na przykład jak wypada dokładność modelu w przypadku 2 technik? Testy A/B mogą jednak porównywać dowolną skończoną liczbę danych.
element akceleratora
Kategoria specjalistycznych komponentów sprzętowych zaprojektowanych do wykonywania kluczowych obliczeń potrzebnych algorytmom uczenia głębokiego.
Układy akceleratorów (lub w skrócie akceleratory) mogą znacznie zwiększyć szybkość i wydajność zadań związanych z trenowaniem i wnioskowaniem w porównaniu z procesorem ogólnego przeznaczenia. Idealnie nadają się do trenowania sieci neuronowych i podobnych zadań wymagających dużej mocy obliczeniowej.
Przykłady układów akceleratorów:
- Jednostki Tensor Processing Unit (TPU) Google z dedykowanym sprzętem do deep learningu.
- Procesory graficzne NVIDIA, które choć początkowo zostały zaprojektowane do przetwarzania grafiki, umożliwiają przetwarzanie równoległe, co może znacznie zwiększyć szybkość przetwarzania.
dokładność
Liczba prawidłowych prognoz klasyfikacji podzielona przez łączną liczbę prognoz. Czyli:
Na przykład model, który dokonał 40 prawidłowych i 10 nieprawidłowych prognoz, ma dokładność:
Klasyfikacja binarna podaje konkretne nazwy różnych kategorii prawidłowych prognoz i nieprawidłowych prognoz. Wzór na dokładność w przypadku klasyfikacji binarnej jest więc taki:
gdzie:
- TP to liczba wyników prawdziwie pozytywnych (poprawnych prognoz).
- TN to liczba wyników prawdziwie negatywnych (prawidłowych prognoz).
- FP to liczba wyników fałszywie pozytywnych (nieprawidłowych prognoz).
- FN to liczba wyników fałszywie negatywnych (nieprawidłowych prognoz).
Porównaj dokładność z precyzją i czułością.
Więcej informacji znajdziesz w sekcji Klasyfikacja: dokładność, czułość, precyzja i powiązane dane w kursie Machine Learning Crash Course.
działanie
W uczeniu przez wzmacnianie mechanizm, za pomocą którego agent przechodzi między stanami środowiska. Agent wybiera działanie na podstawie zasad.
funkcja aktywacji,
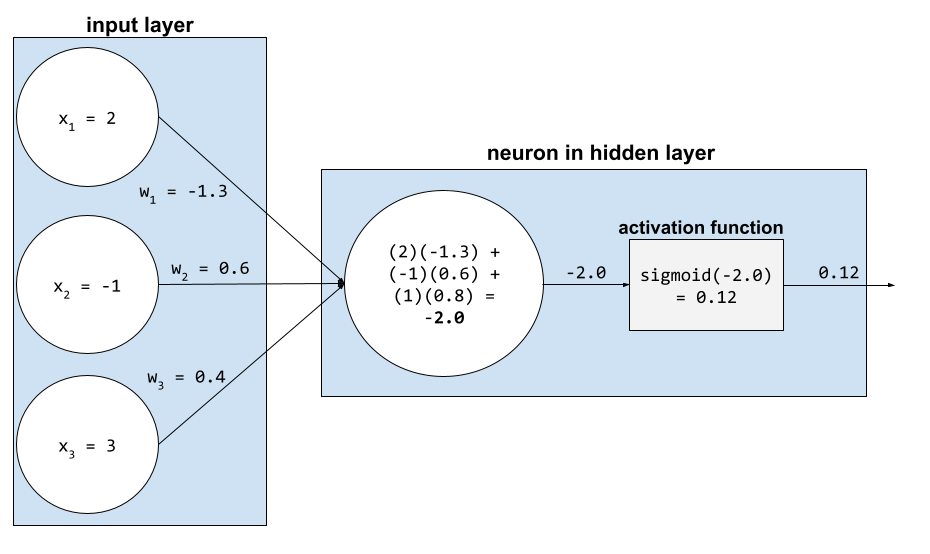
Funkcja, która umożliwia sieciom neuronowym uczenie się nieliniowych (złożonych) zależności między cechami a etykietą.
Popularne funkcje aktywacji to:
Wykresy funkcji aktywacji nigdy nie są pojedynczymi liniami prostymi. Na przykład wykres funkcji aktywacji ReLU składa się z 2 linii prostych:

Wykres funkcji aktywacji sigmoid wygląda tak:

Więcej informacji znajdziesz w sekcji Sieci neuronowe: funkcje aktywacji w kursie Machine Learning Crash Course.
aktywne uczenie się,
Trenowanie, w którym algorytm wybiera część danych, na których się uczy. Aktywne uczenie się jest szczególnie przydatne, gdy oznakowane przykłady są rzadkie lub drogie w uzyskaniu. Zamiast ślepo szukać różnorodnych przykładów z etykietami, algorytm aktywnego uczenia się selektywnie wyszukuje konkretny zakres przykładów, których potrzebuje do uczenia się.
AdaGrad
Zaawansowany algorytm spadku gradientowego, który zmienia skalę gradientów każdego parametru, dzięki czemu każdy parametr ma niezależny współczynnik uczenia. Pełne wyjaśnienie znajdziesz w artykule Adaptive Subgradient Methods for Online Learning and Stochastic Optimization.
adaptacja
Synonim dostrajania lub precyzyjnego dostrajania.
agent
Oprogramowanie, które potrafi analizować multimodalne dane wejściowe użytkownika, aby planować i wykonywać działania w jego imieniu.
W uczeniu przez wzmacnianie agent to podmiot, który korzysta z zasad, aby zmaksymalizować oczekiwany zysk uzyskany w wyniku przejścia między stanami środowiska.
grupowanie aglomeracyjne,
Zobacz klastrowanie hierarchiczne.
wykrywanie anomalii,
Proces identyfikowania wartości odstających. Jeśli na przykład średnia dla danej cechy wynosi 100, a odchylenie standardowe 10, wykrywanie anomalii powinno oznaczyć wartość 200 jako podejrzaną.
AR
Skrót od rzeczywistości rozszerzonej.
obszar pod krzywą precyzji i czułości,
Zobacz PR AUC (obszar pod krzywą PR).
obszar pod krzywą charakterystyki operacyjnej odbiornika
Zobacz AUC (obszar pod krzywą ROC).
ogólna sztuczna inteligencja,
Mechanizm niebędący człowiekiem, który wykazuje szeroki zakres umiejętności rozwiązywania problemów, kreatywności i zdolności adaptacyjnych. Na przykład program wykazujący sztuczną inteligencję ogólną mógłby tłumaczyć tekst, komponować symfonie i osiągać doskonałe wyniki w grach, które nie zostały jeszcze wynalezione.
sztuczna inteligencja
Program lub model niebędący człowiekiem, który potrafi wykonywać złożone zadania. Na przykład program lub model, który tłumaczy tekst, albo program lub model, który identyfikuje choroby na podstawie zdjęć radiologicznych, wykazują cechy sztucznej inteligencji.
Uczenie maszynowe to poddziedzina sztucznej inteligencji. Jednak w ostatnich latach niektóre organizacje zaczęły używać terminów sztuczna inteligencja i uczenie maszynowe zamiennie.
uwaga
Mechanizm używany w sieci neuronowej, który wskazuje znaczenie konkretnego słowa lub jego części. Mechanizm uwagi kompresuje ilość informacji, których model potrzebuje do przewidzenia kolejnego tokena lub słowa. Typowy mechanizm uwagi może składać się z sumy ważonej zbioru danych wejściowych, gdzie waga każdego z nich jest obliczana przez inną część sieci neuronowej.
Zobacz też mechanizm uwagi i mechanizm uwagi z wieloma głowicami, które są podstawowymi elementami transformatorów.
Więcej informacji o mechanizmie samouważności znajdziesz w artykule LLM: What's a large language model? (Duże modele językowe: co to jest duży model językowy?) w kursie Machine Learning Crash Course.
atrybut
Synonim funkcji.
W kontekście sprawiedliwości w uczeniu maszynowym atrybuty często odnoszą się do cech charakterystycznych osób.
próbkowanie atrybutów,
Taktyka trenowania lasu decyzyjnego, w której każde drzewo decyzyjne podczas uczenia się warunku bierze pod uwagę tylko losowy podzbiór możliwych cech. Zwykle w przypadku każdego węzła próbkowany jest inny podzbiór cech. Z kolei podczas trenowania drzewa decyzyjnego bez próbkowania atrybutów w przypadku każdego węzła brane są pod uwagę wszystkie możliwe cechy.
AUC (obszar pod krzywą ROC)
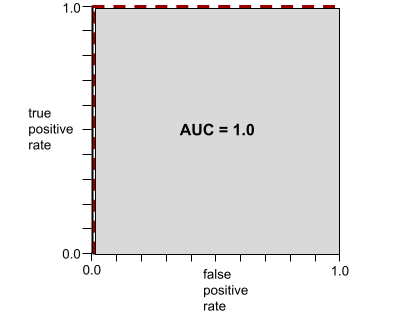
Liczba z zakresu od 0,0 do 1,0 reprezentująca zdolność modelu klasyfikacji binarnej do rozdzielania klas pozytywnych od klas negatywnych. Im bliżej wartości 1,0 jest AUC, tym lepiej model rozróżnia klasy.
Na przykład poniższa ilustracja przedstawia model klasyfikacji, który doskonale rozdziela klasy pozytywne (zielone owale) od klas negatywnych (fioletowe prostokąty). Ten nierealistycznie doskonały model ma wartość AUC równą 1,0:

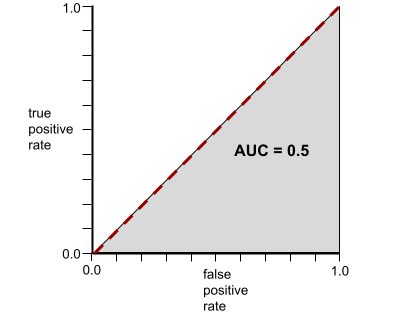
Z kolei poniższa ilustracja przedstawia wyniki modelu klasyfikacji, który generował losowe wyniki. Ten model ma wartość AUC 0,5:

Tak, poprzedni model ma wartość AUC 0,5, a nie 0,0.
Większość modeli znajduje się gdzieś pomiędzy tymi dwoma skrajnościami. Na przykład poniższy model w pewnym stopniu rozdziela wartości pozytywne od negatywnych, dlatego ma wartość AUC między 0,5 a 1,0:

AUC ignoruje każdą wartość ustawioną dla progu klasyfikacji. Zamiast tego AUC uwzględnia wszystkie możliwe progi kwalifikacji.
Więcej informacji znajdziesz w sekcji Klasyfikacja: ROC i AUC w szybkim szkoleniu z uczenia maszynowego.
rzeczywistość rozszerzona
Technologia, która nakłada obraz wygenerowany komputerowo na widok użytkownika w rzeczywistym świecie, tworząc w ten sposób widok złożony.
autoenkoder
System, który uczy się wyodrębniać najważniejsze informacje z danych wejściowych. Autokodery to połączenie enkodera i dekodera. Autoenkodery działają w 2-etapowym procesie:
- Koder mapuje dane wejściowe na (zwykle) stratny format o mniejszej liczbie wymiarów (pośredni).
- Dekoder tworzy stratną wersję oryginalnych danych wejściowych, mapując format o mniejszej liczbie wymiarów na oryginalny format wejściowy o większej liczbie wymiarów.
Autokodery są trenowane kompleksowo, a dekoder próbuje jak najdokładniej odtworzyć oryginalne dane wejściowe z formatu pośredniego kodera. Format pośredni jest mniejszy (ma mniejszą liczbę wymiarów) niż format oryginalny, więc autokoder musi nauczyć się, które informacje wejściowe są niezbędne, a dane wyjściowe nie będą idealnie identyczne z danymi wejściowymi.
Na przykład:
- Jeśli dane wejściowe to grafika, nieprecyzyjna kopia będzie podobna do oryginalnej grafiki, ale nieco zmodyfikowana. Być może niedokładna kopia usuwa szum z oryginalnej grafiki lub wypełnia brakujące piksele.
- Jeśli dane wejściowe to tekst, autokoder wygeneruje nowy tekst, który naśladuje (ale nie jest identyczny z) oryginalny tekst.
Zobacz też wariacyjne autokodery.
automatyczna ocena,
Używanie oprogramowania do oceny jakości danych wyjściowych modelu.
Gdy dane wyjściowe modelu są stosunkowo proste, skrypt lub program może porównać je z wzorcową odpowiedzią. Ten typ automatycznej oceny jest czasami nazywany oceną programową. Do oceny automatycznej często przydają się dane takie jak ROUGE czy BLEU.
Gdy dane wyjściowe modelu są złożone lub nie mają jednej prawidłowej odpowiedzi, automatyczną ocenę przeprowadza czasami osobny program ML zwany automatycznym oceniającym.
Porównaj z oceną przez człowieka.
błąd automatyzacji
Gdy osoba podejmująca decyzję faworyzuje rekomendacje systemu automatycznego podejmowania decyzji w stosunku do informacji uzyskanych bez automatyzacji, nawet jeśli system automatycznego podejmowania decyzji popełnia błędy.
Więcej informacji znajdziesz w module Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
AutoML
Każdy zautomatyzowany proces tworzenia modeli uczenia maszynowego. AutoML może automatycznie wykonywać takie zadania jak:
- Wyszukaj najbardziej odpowiedni model.
- Dostrajanie hiperparametrów.
- przygotowywać dane (w tym przeprowadzać ekstrakcję wyróżników);
- wdrożyć uzyskany model,
AutoML jest przydatny dla badaczy danych, ponieważ pozwala im zaoszczędzić czas i wysiłek podczas tworzenia potoków uczenia maszynowego oraz zwiększyć dokładność prognoz. Jest też przydatne dla osób, które nie są ekspertami, ponieważ ułatwia im wykonywanie skomplikowanych zadań związanych z uczeniem maszynowym.
Więcej informacji znajdziesz w artykule Automated Machine Learning (AutoML) w szybkim szkoleniu z uczenia maszynowego.
ocena automatyczna,
Hybrydowy mechanizm oceny jakości danych wyjściowych modelu generatywnej AI, który łączy ocenę przez człowieka z oceną automatyczną. Automatyczny oceniający to model ML wytrenowany na danych utworzonych na podstawie oceny przez człowieka. W idealnym przypadku narzędzie automatyczne uczy się naśladować weryfikatora.Dostępne są gotowe automatyczne oceny, ale najlepsze z nich są dostosowane do konkretnego zadania, które oceniasz.
model autoregresyjny,
Model, który wyciąga wnioski na podstawie własnych wcześniejszych prognoz. Na przykład autoregresyjne modele językowe przewidują następny token na podstawie wcześniej przewidzianych tokenów. Wszystkie duże modele językowe oparte na architekturze Transformer są autoregresyjne.
Z kolei modele obrazów oparte na GAN zwykle nie są autoregresywne, ponieważ generują obraz w jednym przejściu do przodu, a nie iteracyjnie w krokach. Niektóre modele generowania obrazów są jednak autoregresywne, ponieważ generują obraz etapami.
strata pomocnicza,
Funkcja utraty – używana w połączeniu z główną funkcją utraty modelu sieci neuronowej, która pomaga przyspieszyć trenowanie na wczesnych etapach, gdy wagi są inicjowane losowo.
Pomocnicze funkcje straty przekazują efektywne gradienty do wcześniejszych warstw. Ułatwia to zbieżność podczas trenowania, ponieważ zapobiega problemowi z zanikającym gradientem.
średnia precyzja przy k
Miara podsumowująca skuteczność modelu w przypadku pojedynczego prompta, który generuje wyniki w postaci listy, np. listy rekomendacji książek. Średnia precyzja przy k to średnia wartości precyzji przy k dla każdego trafnego wyniku. Wzór na średnią precyzję przy k to:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
gdzie:
- \(n\) to liczba odpowiednich elementów na liście.
Porównaj z przypominaniem w momencie k.
warunek wyrównany do osi
W drzewie decyzyjnym warunek
obejmujący tylko 1 obiekt. Jeśli na przykład area jest cechą, to warunek wyrównany do osi wygląda tak:
area > 200
Kontrast z warunkiem ukośnym.
B
propagacja wsteczna
Algorytm, który implementuje metodę spadku gradientu w sieciach neuronowych.
Trenowanie sieci neuronowej obejmuje wiele iteracji tego dwuetapowego cyklu:
- Podczas przejścia w przód system przetwarza partię przykładów, aby uzyskać prognozy. System porównuje każdą prognozę z wartością każdej etykiety. Różnica między prognozą a wartością etykiety to funkcja straty dla tego przykładu. System sumuje straty dla wszystkich przykładów, aby obliczyć całkowitą stratę dla bieżącej partii.
- Podczas przejścia wstecznego (propagacji wstecznej) system zmniejsza straty, dostosowując wagi wszystkich neuronów we wszystkich warstwach ukrytych.
Sieci neuronowe często zawierają wiele neuronów w wielu warstwach ukrytych. Każdy z tych neuronów przyczynia się do ogólnej utraty w inny sposób. Algorytm propagacji wstecznej określa, czy zwiększyć, czy zmniejszyć wagi przypisane do poszczególnych neuronów.
Tempo uczenia się to mnożnik, który określa stopień, w jakim każda iteracja wsteczna zwiększa lub zmniejsza każdą wagę. Duże tempo uczenia się zwiększy lub zmniejszy każdą wagę bardziej niż małe tempo uczenia się.
W terminologii rachunku różniczkowego propagacja wsteczna wykorzystuje regułę łańcuchową. Oznacza to, że propagacja wsteczna oblicza pochodną cząstkową błędu względem każdego parametru.
Jeszcze kilka lat temu specjaliści ds. uczenia maszynowego musieli pisać kod, aby wdrożyć propagację wsteczną. Nowoczesne interfejsy API ML, takie jak Keras, implementują propagację wsteczną. Uff...
Więcej informacji znajdziesz w sekcji Sieci neuronowe w Szybkim szkoleniu z uczenia maszynowego.
bagging
Metoda trenowania zespołu, w którym każdy model składowy jest trenowany na losowym podzbiorze przykładów treningowych próbkowanych z powtórzeniami. Na przykład las losowy to zbiór drzew decyzyjnych wytrenowanych za pomocą metody baggingu.
Termin bagging to skrót od bootstrap aggregating.
Więcej informacji znajdziesz w sekcji Las losowy w kursie Decision Forests.
worek słów,
reprezentacja słów w wyrażeniu lub fragmencie tekstu, niezależnie od kolejności; Na przykład model bag-of-words reprezentuje te 3 wyrażenia w identyczny sposób:
- pies skacze,
- przeskakuje psa,
- pies przeskakuje
Każde słowo jest mapowane na indeks w wektorze rzadkim, który zawiera indeks dla każdego słowa w słowniku. Na przykład fraza pies skacze jest mapowana na wektor cech z wartościami niezerowymi na 3 indeksach odpowiadających słowom pies, skacze i the. Wartość różna od zera może być dowolną z tych wartości:
- 1 – oznacza obecność słowa.
- Liczba wystąpień słowa w zbiorze. Jeśli na przykład fraza to the maroon dog is a dog with maroon fur, słowa maroon i dog będą miały wartość 2, a pozostałe słowa – 1.
- Inna wartość, np. logarytm liczby wystąpień słowa w zbiorze.
bazowa
Model używany jako punkt odniesienia do porównywania skuteczności innego modelu (zwykle bardziej złożonego). Na przykład model regresji logistycznej może być dobrym modelem bazowym dla modelu głębokiego.
W przypadku konkretnego problemu wartość bazowa pomaga deweloperom modeli określić minimalną oczekiwaną skuteczność, jaką musi osiągnąć nowy model, aby był przydatny.
model podstawowy,
Wytrenowany model, który może służyć jako punkt wyjścia do dostrajania pod kątem konkretnych zadań lub zastosowań.
Zobacz też wstępnie wytrenowany model i model podstawowy.
wsad
Zestaw przykładów używanych w jednej iteracji trenowania. Rozmiar wsadu określa liczbę przykładów w wsadzie.
Wyjaśnienie, jak partia jest powiązana z epoką, znajdziesz w tym artykule.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
wnioskowanie zbiorcze
Proces wyciągania wniosków na podstawie wielu nieoznaczonych przykładów podzielonych na mniejsze podzbiory („partie”).
Wnioskowanie wsadowe może korzystać z funkcji równoległego przetwarzania chipów akceleratora. Oznacza to, że wiele akceleratorów może jednocześnie generować prognozy na podstawie różnych partii nieoznaczonych przykładów, co znacznie zwiększa liczbę prognoz na sekundę.
Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: statyczne i dynamiczne wnioskowanie w kursie Machine Learning Crash Course.
normalizacja wsadowa,
Normalizowanie danych wejściowych lub wyjściowych funkcji aktywacji w warstwie ukrytej. Normalizacja wsadowa może przynieść te korzyści:
- Zwiększanie stabilności sieci neuronowych przez ochronę przed wartościami odstającymi wag.
- Włącz wyższe współczynniki uczenia się, co może przyspieszyć trenowanie.
- Zmniejsz nadmierne dopasowanie.
wielkość wsadu
Liczba przykładów w partii. Jeśli na przykład rozmiar partii wynosi 100, model przetwarza 100 przykładów na iterację.
Oto popularne strategie dotyczące wielkości wsadu:
- Stochastyczny spadek wzdłuż gradientu (SGD), w którym rozmiar partii wynosi 1.
- Pełny wsad, w którym rozmiar wsadu jest równy liczbie przykładów w całym zbiorze treningowym. Jeśli np. zbiór treningowy zawiera milion przykładów, rozmiar partii będzie wynosić milion przykładów. Pełna partia jest zwykle nieefektywną strategią.
- mini-batch, w którym rozmiar partii wynosi zwykle od 10 do 1000. Mini-batch to zwykle najbardziej efektywna strategia.
Więcej informacji znajdziesz poniżej:
- Produkcyjne systemy uczenia maszynowego: wnioskowanie statyczne a dynamiczne w szybkim szkoleniu z uczenia maszynowego.
- Poradnik dotyczący dostrajania uczenia głębokiego
Bayesowska sieć neuronowa
Jest to probabilistyczna sieć neuronowa, która uwzględnia niepewność wag i wyników. Standardowy model regresji sieci neuronowej zwykle przewiduje wartość skalarną, np. standardowy model przewiduje cenę domu w wysokości 853 000 zł. Z kolei bayesowska sieć neuronowa przewiduje rozkład wartości. Na przykład model bayesowski przewiduje cenę domu na poziomie 853 tys. zł z odchyleniem standardowym wynoszącym 67,2 tys. zł.
Bayesowska sieć neuronowa opiera się na twierdzeniu Bayesa do obliczania niepewności wag i prognoz. Bayesowska sieć neuronowa może być przydatna, gdy ważne jest określenie niepewności, np. w modelach związanych z farmaceutykami. Bayesowskie sieci neuronowe mogą też zapobiegać przetrenowaniu.
Optymalizacja bayesowska
Probabilistyczny model regresji to technika optymalizacji kosztownych obliczeniowo funkcji celu, która zamiast tego optymalizuje funkcję zastępczą, która określa ilościowo niepewność za pomocą techniki uczenia bayesowskiego. Optymalizacja bayesowska jest bardzo kosztowna, dlatego zwykle stosuje się ją do optymalizacji zadań, których ocena jest kosztowna i które mają niewielką liczbę parametrów, np. do wybierania hiperparametrów.
Równanie Bellmana
W uczeniu ze wzmocnieniem optymalna funkcja Q spełnia następującą tożsamość:
\[Q(s, a) = r(s, a) + \gamma \mathbb{E}_{s'|s,a} \max_{a'} Q(s', a')\]
Algorytmy uczenia się przez wzmacnianie stosują tę tożsamość do tworzenia uczenia się Q za pomocą tej reguły aktualizacji:
\[Q(s,a) \gets Q(s,a) + \alpha \left[r(s,a) + \gamma \displaystyle\max_{\substack{a_1}} Q(s',a') - Q(s,a) \right] \]
Równanie Bellmana ma zastosowanie nie tylko w uczeniu ze wzmocnieniem, ale też w programowaniu dynamicznym. Zobacz artykuł o równaniu Bellmana w Wikipedii.
BERT (Bidirectional Encoder Representations from Transformers)
Architektura modelu do reprezentacji tekstu. Wytrenowany model BERT może być częścią większego modelu do klasyfikacji tekstu lub innych zadań uczenia maszynowego.
BERT ma te cechy:
- Korzysta z architektury Transformer, a więc opiera się na samouwadze.
- Wykorzystuje enkoder modelu Transformer. Zadaniem kodera jest tworzenie dobrych reprezentacji tekstu, a nie wykonywanie konkretnego zadania, takiego jak klasyfikacja.
- Jest dwukierunkowy.
- Wykorzystuje maskowanie w przypadku trenowania bez nadzoru.
Odmiany BERT obejmują:
Więcej informacji o BERT znajdziesz w artykule Open Sourcing BERT: State-of-the-Art Pre-training for Natural Language Processing.
uprzedzenia (etyka/uczciwość),
1. Tworzenie stereotypów lub faworyzowanie określonych rzeczy, ludzi lub grup względem innych. Te odchylenia mogą wpływać na zbieranie i interpretowanie danych, projektowanie systemu oraz sposób, w jaki użytkownicy z nim wchodzą w interakcje. Formy tego typu błędu obejmują:
- błąd automatyzacji
- efekt potwierdzenia
- błąd eksperymentatora
- błąd uogólnienia
- nieświadome uprzedzenia
- stronniczość wewnątrzgrupowa,
- błąd jednorodności grupy obcej,
2. Błąd systematyczny wprowadzony przez procedurę próbkowania lub raportowania. Formy tego typu błędu obejmują:
- błąd pokrycia
- błąd braku odpowiedzi,
- błąd związany z udziałem
- błąd raportowania
- błąd próbkowania
- błąd doboru
Nie należy go mylić z terminem „uprzedzenie” w modelach uczenia maszynowego ani z uprzedzeniem w prognozach.
Więcej informacji znajdziesz w sekcji Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
wyraz wolny (matematyka) lub wyraz wolny
Punkt przecięcia lub przesunięcie względem punktu początkowego. Uprzedzenie to parametr w modelach uczenia maszynowego, który jest oznaczany jednym z tych symboli:
- b
- w0
Na przykład w tej formule wyraz b oznacza odchylenie:
W przypadku prostej dwuwymiarowej odchylenie oznacza po prostu „punkt przecięcia z osią Y”. Na przykład odchylenie prostej na poniższej ilustracji wynosi 2.
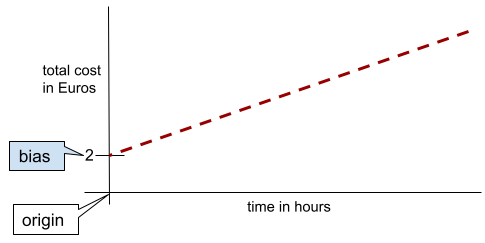
Występuje odchylenie, ponieważ nie wszystkie modele zaczynają się od punktu początkowego (0,0). Załóżmy na przykład, że wejście do parku rozrywki kosztuje 2 PLN, a każda dodatkowa godzina pobytu klienta to 0,5 PLN. Dlatego model mapujący koszt całkowity ma odchylenie równe 2, ponieważ najniższy koszt to 2 euro.
Uprzedzeń nie należy mylić z uprzedzeniami w kontekście etyki i obiektywności ani z uprzedzeniami w prognozach.
Więcej informacji znajdziesz w sekcji Regresja liniowa w szybkim szkoleniu z uczenia maszynowego.
dwukierunkowe,
Termin używany do opisywania systemu, który ocenia tekst poprzedzający i następujący po docelowej sekcji tekstu. Z kolei system jednokierunkowy ocenia tylko tekst, który poprzedza docelowy fragment tekstu.
Weźmy na przykład zamaskowany model językowy, który musi określić prawdopodobieństwa słowa lub słów reprezentujących podkreślenie w tym pytaniu:
Co się z tobą dzieje?
Jednokierunkowy model językowy musiałby opierać swoje prawdopodobieństwa tylko na kontekście zapewnianym przez słowa „What”, „is” i „the”. Z kolei dwukierunkowy model językowy może też uzyskać kontekst z wyrazów „z” i „Tobą”, co może mu pomóc w generowaniu lepszych prognoz.
dwukierunkowy model językowy
Model językowy, który określa prawdopodobieństwo wystąpienia danego tokena w określonym miejscu w fragmencie tekstu na podstawie poprzedzającego i następującego tekstu.
bigram
N-gram, w którym N=2.
klasyfikacja binarna,
Typ zadania klasyfikacji, które przewiduje jedną z 2 wykluczających się wzajemnie klas:
Na przykład te 2 modele uczenia maszynowego wykonują klasyfikację binarną:
- Model, który określa, czy wiadomości e-mail to spam (klasa pozytywna) czy nie spam (klasa negatywna).
- Model, który ocenia objawy medyczne, aby określić, czy dana osoba ma konkretną chorobę (klasa pozytywna), czy nie (klasa negatywna).
W przeciwieństwie do klasyfikacji wieloklasowej.
Zobacz też regresję logistyczną i próg klasyfikacji.
Więcej informacji znajdziesz w sekcji Klasyfikacja w Szybkim szkoleniu z uczenia maszynowego.
warunek binarny
W drzewie decyzyjnym warunek, który ma tylko 2 możliwe wyniki, zwykle tak lub nie. Na przykład warunek binarny to:
temperature >= 100
Porównaj z warunkiem niebinarnym.
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
grupowanie
Synonim słowa grupowanie.
model czarnej skrzynki
Model, którego „rozumowanie” jest niemożliwe lub trudne do zrozumienia dla ludzi. Oznacza to, że chociaż ludzie mogą zobaczyć, jak prompty wpływają na odpowiedzi, nie mogą dokładnie określić, w jaki sposób model typu black box określa odpowiedź. Innymi słowy, model typu „czarna skrzynka” nie ma interpretowalności.
Większość modeli głębokich i dużych modeli językowych to czarne skrzynki.
BLEU (Bilingual Evaluation Understudy)
Wskaźnik z zakresu od 0,0 do 1,0 służący do oceny tłumaczeń maszynowych, np. z języka hiszpańskiego na japoński.
Aby obliczyć wynik, BLEU porównuje tłumaczenie modelu ML (wygenerowany tekst) z tłumaczeniem eksperta (tekst referencyjny). Stopień dopasowania n-gramów w wygenerowanym tekście i tekście referencyjnym określa wynik BLEU.
Oryginalny artykuł na temat tego wskaźnika to BLEU: a Method for Automatic Evaluation of Machine Translation.
Zobacz też BLEURT.
BLEURT (Bilingual Evaluation Understudy from Transformers)
Wskaźnik służący do oceny tłumaczeń maszynowych z jednego języka na inny, zwłaszcza z języka angielskiego i na język angielski.
W przypadku tłumaczeń na język angielski i z języka angielskiego BLEURT jest bardziej zgodny z ocenami ludzi niż BLEU. W przeciwieństwie do BLEU wskaźnik BLEURT kładzie nacisk na podobieństwa semantyczne (znaczeniowe) i może uwzględniać parafrazy.
BLEURT korzysta z wstępnie wytrenowanego dużego modelu językowego (dokładnie BERT), który jest następnie dostrajany na podstawie tekstów przetłumaczonych przez ludzi.
Oryginalny artykuł na temat tego wskaźnika to BLEURT: Learning Robust Metrics for Text Generation (BLEURT: uczenie się niezawodnych wskaźników generowania tekstu).
podbijanie
Technika uczenia maszynowego, która iteracyjnie łączy zestaw prostych i niezbyt dokładnych modeli klasyfikacji (nazywanych „słabymi klasyfikatorami”) w model klasyfikacji o wysokiej dokładności („silny klasyfikator”) przez zwiększanie wagi przykładów, które model obecnie błędnie klasyfikuje.
Więcej informacji znajdziesz w sekcji Gradient Boosted Decision Trees w kursie Decision Forests.
ramka ograniczająca
Współrzędne (x, y) prostokąta otaczającego obszar zainteresowania na obrazie, np. psa na obrazie poniżej.

nadawanie,
Rozszerzanie kształtu operandu w operacji matematycznej na macierzach do wymiarów zgodnych z tą operacją. Na przykład w algebrze liniowej oba operandy w operacji dodawania macierzy muszą mieć te same wymiary. W związku z tym nie możesz dodać macierzy o kształcie (m, n) do wektora o długości n. Rozgłaszanie umożliwia tę operację poprzez wirtualne rozszerzenie wektora o długości n do macierzy o kształcie (m, n) przez powielanie tych samych wartości w każdej kolumnie.
Więcej informacji znajdziesz w tym opisie rozgłaszania w NumPy.
skategoryzowanie w przedziałach
Przekształcanie pojedynczej cechy w wiele cech binarnych, zwanych zasobnikami lub przedziałami, zwykle na podstawie zakresu wartości. Przycięta cecha jest zwykle cechą ciągłą.
Na przykład zamiast przedstawiać temperaturę jako pojedynczą ciągłą cechę zmiennoprzecinkową, możesz podzielić zakresy temperatur na odrębne przedziały, takie jak:
- „Zimno” to temperatura ≤ 10°C.
- Przedział „umiarkowany” to 11–24 stopnie Celsjusza.
- „Ciepło” to temperatura ≥ 25°C.
Model będzie traktować każdą wartość w tym samym przedziale identycznie. Na przykład wartości 13 i 22 należą do tego samego przedziału klimatu umiarkowanego, więc model traktuje je identycznie.
Więcej informacji znajdziesz w sekcji Dane liczbowe: dzielenie na przedziały w szybkim szkoleniu z uczenia maszynowego.
K
warstwa kalibracji
Korekta po prognozie, zwykle uwzględniająca odchylenie prognozy. Skorygowane prognozy i prawdopodobieństwa powinny być zgodne z rozkładem zaobserwowanego zbioru etykiet.
generowanie kandydatów,
Początkowy zestaw rekomendacji wybrany przez system rekomendacji. Weźmy na przykład księgarnię, która oferuje 100 tys. tytułów. W fazie generowania kandydatów tworzona jest znacznie mniejsza lista odpowiednich książek dla danego użytkownika, np. 500. Ale nawet 500 książek to za dużo, aby polecić je użytkownikowi. Kolejne, bardziej kosztowne etapy systemu rekomendacji (takie jak ocenianie i ponowne rankingowanie) zmniejszają liczbę tych 500 rekomendacji do znacznie mniejszego, bardziej przydatnego zestawu.
Więcej informacji znajdziesz w omówieniu generowania kandydatów w kursie Systemy rekomendacji.
próbkowanie kandydatów,
Optymalizacja w czasie trenowania, która oblicza prawdopodobieństwo dla wszystkich etykiet pozytywnych, np. za pomocą funkcji softmax, ale tylko w przypadku losowej próbki etykiet negatywnych. Na przykład w przypadku przykładu z etykietami beagle i dog próbkowanie kandydatów oblicza przewidywane prawdopodobieństwa i odpowiednie składniki funkcji straty dla tych etykiet:
- beagle
- pies
- losowy podzbiór pozostałych klas wyników negatywnych (np. kot, lizak, płot);
Chodzi o to, że klasy negatywne mogą się uczyć na podstawie rzadszego negatywnego wzmocnienia, o ile klasy pozytywne zawsze otrzymują odpowiednie pozytywne wzmocnienie. Zostało to potwierdzone empirycznie.
Próbkowanie kandydatów jest bardziej wydajne obliczeniowo niż algorytmy trenujące, które obliczają prognozy dla wszystkich klas negatywnych, zwłaszcza gdy liczba klas negatywnych jest bardzo duża.
dane kategorialne,
Cechy mające określony zestaw możliwych wartości. Rozważmy na przykład cechę kategorialną o nazwie traffic-light-state, która może przyjmować tylko jedną z tych 3 wartości:
redyellowgreen
Przedstawiając traffic-light-state jako cechę kategoryczną, model może się nauczyć różnych wpływów red, green i yellow na zachowanie kierowcy.
Funkcje kategorialne są czasami nazywane funkcjami dyskretnymi.
Kontrast z danymi liczbowymi.
Więcej informacji znajdziesz w sekcji Praca z danymi kategorialnymi w kursie Machine Learning Crash Course.
przyczynowy model językowy,
Synonim jednokierunkowego modelu językowego.
Więcej informacji o różnych podejściach do modelowania języka znajdziesz w artykule o dwukierunkowym modelu językowym.
centroid
Środek klastra określony przez algorytm k-średnich lub k-median. Jeśli na przykład k = 3, algorytm k-średnich lub k-median znajdzie 3 środki skupień.
Więcej informacji znajdziesz w sekcji Algorytmy klastrowania w kursie Klastrowanie.
grupowanie oparte na centroidach,
Kategoria algorytmów grupowania, które porządkują dane w niehierarchiczne klastry. Najczęściej używanym algorytmem grupującym opartym na centroidach jest k-średnich.
W przeciwieństwie do algorytmów grupowania hierarchicznego.
Więcej informacji znajdziesz w sekcji Algorytmy klastrowania w kursie Klastrowanie.
wykorzystanie w prompcie łańcucha myśli
Technika inżynierii promptów, która zachęca duży model językowy (LLM) do wyjaśniania swojego rozumowania krok po kroku. Rozważmy na przykład ten prompt, zwracając szczególną uwagę na drugie zdanie:
Jakie przeciążenie odczuje kierowca samochodu, który przyspiesza od 0 do 96 km/h w 7 sekund? W odpowiedzi podaj wszystkie istotne obliczenia.
Odpowiedź modelu LLM prawdopodobnie:
- Wyświetl sekwencję wzorów fizycznych, wstawiając wartości 0, 60 i 7 w odpowiednich miejscach.
- Wyjaśnij, dlaczego wybrał te formuły i co oznaczają poszczególne zmienne.
Promptowanie z użyciem ciągu myśli zmusza LLM do wykonania wszystkich obliczeń, co może prowadzić do uzyskania bardziej poprawnej odpowiedzi. Dodatkowo podpowiedzi typu „chain-of-thought” umożliwiają użytkownikowi sprawdzenie kroków LLM, aby określić, czy odpowiedź jest sensowna.
czat
Treść dialogu z systemem ML, zwykle z dużym modelem językowym. Poprzednia interakcja na czacie (to, co zostało wpisane, i jak zareagował duży model językowy) staje się kontekstem dla kolejnych części czatu.
Czatbot to aplikacja oparta na dużym modelu językowym.
punkt kontroli
Dane, które rejestrują stan parametrów modelu podczas trenowania lub po jego zakończeniu. Na przykład podczas treningu możesz:
- zatrzymać trenowanie, być może celowo lub w wyniku pewnych błędów.
- Zarejestruj punkt kontrolny.
- Później możesz ponownie wczytać punkt kontrolny, być może na innym sprzęcie.
- Rozpocznij ponowne trenowanie.
klasa
Kategoria, do której może należeć etykieta. Na przykład:
- W modelu klasyfikacji binarnej, który wykrywa spam, 2 klasy mogą być oznaczone jako spam i nie spam.
- W modelu klasyfikacji wieloklasowej, który identyfikuje rasy psów, klasy mogą być pudel, beagle, mops itp.
Model klasyfikacji prognozuje klasę. Z kolei model regresji prognozuje liczbę, a nie klasę.
Więcej informacji znajdziesz w sekcji Klasyfikacja w Szybkim szkoleniu z uczenia maszynowego.
zbiór danych z równomiernym rozkładem klas,
Zbiór danych zawierający etykiety kategorialne, w którym liczba instancji każdej kategorii jest w przybliżeniu równa. Rozważmy na przykład zbiór danych botanicznych, którego etykieta binarna może mieć wartość roślina rodzima lub roślina nierodzima:
- Zbiór danych zawierający 515 roślin rodzimych i 485 roślin nierodzimych jest zbiorem danych o zrównoważonych klasach.
- Zbiór danych zawierający 875 roślin rodzimych i 125 roślin nierodzimych to zbiór danych z nierównowagą klas.
Nie ma formalnej granicy między zbiorami danych o zrównoważonych klasach a zbiorami danych o niezrównoważonych klasach. Różnica ta ma znaczenie tylko wtedy, gdy model wytrenowany na zbiorze danych o dużej nierównowadze klas nie może zbiegać się do określonej wartości. Szczegółowe informacje znajdziesz w sekcji Zbiory danych: niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
model klasyfikacji,
Model, którego prognozą jest klasa. Na przykład modelami klasyfikacji są:
- Model, który przewiduje język zdania wejściowego (francuski? hiszpański? włoski?).
- Model, który przewiduje gatunek drzewa (klon? Dąb? Baobab?).
- Model, który prognozuje klasę pozytywną lub negatywną dla określonego stanu zdrowia.
Modele regresji przewidują liczby, a nie klasy.
Dwa popularne rodzaje modeli klasyfikacji to:
próg klasyfikacji
W klasyfikacji binarnej liczba z zakresu od 0 do 1, która przekształca surowe dane wyjściowe modelu regresji logistycznej w prognozę klasy pozytywnej lub klasy negatywnej. Pamiętaj, że próg klasyfikacji to wartość wybierana przez człowieka, a nie wartość wybierana podczas trenowania modelu.
Model regresji logistycznej zwraca wartość surową z zakresu od 0 do 1. Następnie:
- Jeśli ta wartość surowa jest większa od progu klasyfikacji, prognozowana jest klasa pozytywna.
- Jeśli ta wartość surowa jest mniejsza od progu klasyfikacji, przewidywana jest klasa negatywna.
Załóżmy na przykład, że próg klasyfikacji wynosi 0,8. Jeśli wartość surowa wynosi 0,9, model prognozuje klasę pozytywną. Jeśli wartość surowa wynosi 0,7, model prognozuje klasę negatywną.
Wybór progu klasyfikacji ma duży wpływ na liczbę wyników fałszywie pozytywnych i wyników fałszywie negatywnych.
Więcej informacji znajdziesz w sekcji Progi i macierz pomyłek w szybkim szkoleniu z uczenia maszynowego.
klasyfikator
Potoczne określenie modelu klasyfikacji.
zbiór danych z nierównomiernym rozkładem klas,
Zbiór danych do klasyfikacji, w którym łączna liczba etykiet każdej klasy znacznie się różni. Rozważmy na przykład zbiór danych klasyfikacji binarnej, którego 2 etykiety są podzielone w ten sposób:
- 1 000 000 etykiet wartości ujemnych
- 10 etykiet wartości dodatnich
Stosunek etykiet negatywnych do pozytywnych wynosi 100 tys. do 1, więc jest to zbiór danych z nierównowagą klas.
Natomiast ten zbiór danych jest zrównoważony pod względem klas, ponieważ stosunek etykiet negatywnych do pozytywnych jest stosunkowo bliski 1:
- 517 etykiet wartości ujemnych
- 483 etykiety wartości dodatnich
Zbiory danych z wieloma klasami mogą też być niezrównoważone pod względem klas. Na przykład ten wieloklasowy zbiór danych do klasyfikacji jest również niezrównoważony, ponieważ jedna etykieta ma znacznie więcej przykładów niż pozostałe dwie:
- 1 000 000 etykiet z klasą „zielony”
- 200 etykiet z klasą „fioletowy”
- 350 etykiet z klasą „pomarańczowy”
Trenowanie zbiorów danych z nierównomiernym rozkładem klas może być szczególnie trudne. Więcej informacji znajdziesz w sekcji Niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
Zobacz też entropię, klasę większościową i klasę mniejszościową.
obcinanie,
Technika radzenia sobie z wartościami odstającymi, która polega na wykonaniu jednej lub obu tych czynności:
- Zmniejszanie wartości cechy, które są większe niż maksymalny próg, do tego progu.
- Zwiększanie wartości cech, które są mniejsze niż próg minimalny, do tego progu.
Załóżmy na przykład, że <0,5% wartości dla danej cechy wypada poza zakresem 40–60. W takim przypadku możesz wykonać te czynności:
- Wszystkie wartości powyżej 60 (maksymalnego progu) zostaną przycięte do 60.
- Wszystkie wartości poniżej 40 (minimalnego progu) zostaną zaokrąglone do 40.
Wartości odstające mogą uszkodzić modele, czasami powodując przepełnienie wag podczas trenowania. Niektóre wartości odstające mogą też znacznie zaniżać wskaźniki takie jak dokładność. Ograniczanie jest powszechną metodą ograniczania szkód.
Obcinanie gradientu wymusza podczas trenowania wartości gradientu w wyznaczonym zakresie.
Więcej informacji znajdziesz w sekcji Dane liczbowe: normalizacja w kursie Machine Learning Crash Course.
Cloud TPU
Specjalistyczny akcelerator sprzętowy zaprojektowany z myślą o przyspieszaniu zadań systemów uczących się w Google Cloud.
grupowanie,
Grupowanie powiązanych przykładów, zwłaszcza podczas uczenia bez nadzoru. Po zgrupowaniu wszystkich przykładów osoba może opcjonalnie przypisać znaczenie do każdego klastra.
Istnieje wiele algorytmów grupowania. Na przykład algorytm k-średnich grupuje przykłady na podstawie ich odległości od centroidu, jak pokazano na tym diagramie:

Badacz może następnie przejrzeć klastry i na przykład oznaczyć klaster 1 jako „karłowate drzewa”, a klaster 2 jako „drzewa pełnowymiarowe”.
Inny przykład: algorytm klastrowania oparty na odległości przykładu od punktu środkowego, przedstawiony w ten sposób:

Więcej informacji znajdziesz w kursie o klastrowaniu.
koadaptacja,
Niepożądane zachowanie, w którym neurony przewidują wzorce w danych treningowych, opierając się niemal wyłącznie na wynikach określonych innych neuronów, zamiast na zachowaniu całej sieci. Jeśli w danych weryfikacyjnych nie ma wzorców, które powodują współadaptację, współadaptacja powoduje nadmierne dopasowanie. Regularyzacja przez wyłączanie zmniejsza współadaptację, ponieważ wyłączanie sprawia, że neurony nie mogą polegać wyłącznie na innych neuronach.
filtrowanie oparte na współpracy,
Tworzenie prognoz dotyczących zainteresowań jednego użytkownika na podstawie zainteresowań wielu innych użytkowników. Filtrowanie oparte na współpracy jest często stosowane w systemach rekomendacji.
Więcej informacji znajdziesz w sekcji Filtrowanie współużytkowników w kursie Systemy rekomendacji.
model kompaktowy,
Każdy mały model przeznaczony do uruchamiania na małych urządzeniach o ograniczonych zasobach obliczeniowych. Na przykład modele kompaktowe mogą działać na telefonach komórkowych, tabletach lub systemach wbudowanych.
compute
(Rzeczownik) Zasoby obliczeniowe używane przez model lub system, takie jak moc obliczeniowa, pamięć i miejsce na dane.
Zobacz układy akceleratora.
dryf koncepcji,
zmiana relacji między cechami a etykietą; Z czasem zmiana koncepcji obniża jakość modelu.
Podczas trenowania model uczy się relacji między cechami a ich etykietami w zbiorze treningowym. Jeśli etykiety w zbiorze treningowym są dobrym przybliżeniem rzeczywistości, model powinien generować dobre prognozy dotyczące świata rzeczywistego. Jednak z powodu zmiany koncepcji prognozy modelu z czasem ulegają pogorszeniu.
Rozważmy na przykład binarny model klasyfikacji, który prognozuje, czy dany model samochodu jest „oszczędny”. Oznacza to, że funkcje mogą być:
- waga samochodu
- kompresja silnika,
- transmission type
gdy etykieta jest:
- oszczędny
- nieoszczędny,
Koncepcja „samochodu o niskim zużyciu paliwa” stale się jednak zmienia. Model samochodu oznaczony w 1994 r. jako oszczędny w 2024 r. prawie na pewno zostałby oznaczony jako nieoszczędny. Model, w którym występuje zmiana koncepcji, z czasem tworzy coraz mniej przydatne prognozy.
Porównaj z niestacjonarnością.
warunek
W drzewie decyzyjnym każdy węzeł, który przeprowadza test. Na przykład to drzewo decyzyjne zawiera 2 warunki:

Warunek jest też nazywany podziałem lub testem.
Warunek kontrastu z leaf.
Zobacz także:
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
konfabulacja
Synonim słowa halucynacja.
Termin „konfabulacja” jest prawdopodobnie bardziej precyzyjny niż „halucynacja”. Najpierw jednak popularność zyskały halucynacje.
konfiguracja
Proces przypisywania początkowych wartości właściwości używanych do trenowania modelu, w tym:
- warstwy, z których składa się model,
- lokalizację danych,
- hiperparametry, takie jak:
W projektach uczenia maszynowego konfigurację można przeprowadzić za pomocą specjalnego pliku konfiguracji lub bibliotek konfiguracji, takich jak:
efekt potwierdzenia,
to tendencja do wyszukiwania, interpretowania, faworyzowania i zapamiętywania informacji w sposób, który potwierdza wcześniejsze przekonania lub hipotezy. Deweloperzy systemów uczących się mogą nieumyślnie zbierać lub oznaczać dane w sposób, który wpływa na wynik potwierdzający ich dotychczasowe przekonania. Efekt potwierdzenia to forma nieświadomych uprzedzeń.
Błąd eksperymentatora to forma efektu potwierdzenia, w której eksperymentator kontynuuje trenowanie modeli, dopóki nie potwierdzi wcześniejszej hipotezy.
tablica pomyłek,
Tabela N×N, która podsumowuje liczbę prawidłowych i nieprawidłowych prognoz dokonanych przez model klasyfikacji. Rozważmy na przykład tę tablicę pomyłek dla modelu klasyfikacji binarnej:
| Guz (prognozowany) | Non-Tumor (predicted) | |
|---|---|---|
| Guz (dane podstawowe) | 18 (TP) | 1 (FN) |
| Brak nowotworu (dane podstawowe) | 6 (FP) | 452 (TN) |
Z powyższej tablicy pomyłek wynika, że:
- Spośród 19 prognoz, w których dane podstawowe wskazywały na nowotwór, model prawidłowo sklasyfikował 18 przypadków, a nieprawidłowo – 1.
- Spośród 458 prognoz, w których dane podstawowe (ground truth) wskazywały na brak guza, model prawidłowo sklasyfikował 452 prognozy, a nieprawidłowo – 6.
Tablica pomyłek w przypadku problemu z klasyfikacją wieloklasową może pomóc w identyfikowaniu wzorców błędów. Rozważmy na przykład tę macierz pomyłek dla modelu klasyfikacji wieloklasowej z 3 klasami, który kategoryzuje 3 różne rodzaje irysów (Virginica, Versicolor i Setosa). Gdy danymi podstawowymi była odmiana Virginica, tablica pomyłek pokazuje, że model znacznie częściej błędnie przewidywał odmianę Versicolor niż Setosa:
| Setosa (przewidywany) | Versicolor (prognozowane) | Virginica (przewidywane) | |
|---|---|---|---|
| Setosa (dane podstawowe) | 88 | 12 | 0 |
| Versicolor (dane podstawowe) | 6 | 141 | 7 |
| Virginica (dane podstawowe) | 2 | 27 | 109 |
Na przykład macierz pomyłek może ujawnić, że model wytrenowany do rozpoznawania odręcznych cyfr ma tendencję do błędnego przewidywania cyfry 9 zamiast 4 lub cyfry 1 zamiast 7.
Macierze pomyłek zawierają wystarczająco dużo informacji, aby obliczyć różne wskaźniki skuteczności, w tym precyzję i czułość.
analiza składniowa
dzielenie zdania na mniejsze struktury gramatyczne („składniki”); Późniejsza część systemu uczenia maszynowego, np. model rozumienia języka naturalnego, może łatwiej analizować składniki niż oryginalne zdanie. Na przykład rozważmy to zdanie:
Moja przyjaciółka adoptowała dwa koty.
Parser składniowy może podzielić to zdanie na 2 składniki:
- Mój przyjaciel to grupa nominalna.
- adopted two cats to fraza czasownikowa.
Te elementy można podzielić na mniejsze. Na przykład wyrażenie czasownikowe
zaadoptowała dwa koty,
można podzielić na:
- adopted to czasownik.
- dwa koty to kolejny rzeczownik.
kontekstowy wektor dystrybucyjny języka
Osadzenie, które jest bliskie „rozumieniu” słów i wyrażeń w sposób, w jaki robią to osoby biegle posługujące się danym językiem. Osadzenia języka w kontekście potrafią zrozumieć złożoną składnię, semantykę i kontekst.
Rozważmy na przykład wektory dystrybucyjne angielskiego słowa cow. Starsze wektory dystrybucyjne, takie jak word2vec, mogą reprezentować słowa w języku angielskim w taki sposób, że odległość w przestrzeni wektorów dystrybucyjnych od cow do bull jest podobna do odległości od ewe (owca) do ram (baran) lub od female do male. Osadzenia językowe uwzględniające kontekst mogą pójść o krok dalej i rozpoznać, że osoby anglojęzyczne czasami używają słowa cow w znaczeniu „krowa” lub „byk”.
okno kontekstu
Liczba tokenów, które model może przetworzyć w ramach danego promptu. Im większe okno kontekstu, tym więcej informacji może wykorzystać model, aby udzielać spójnych i konsekwentnych odpowiedzi na prompt.
cecha ciągła,
Cechy zmiennoprzecinkowe z nieskończonym zakresem możliwych wartości, np. temperatura lub waga.
Kontrast z funkcją dyskretną.
dobór wygodny
Używanie zbioru danych, który nie został zebrany w sposób naukowy, do przeprowadzania szybkich eksperymentów. Później konieczne jest przejście na zbiór danych zebranych w sposób naukowy.
zbieżność
Stan osiągany, gdy wartości funkcji straty zmieniają się bardzo nieznacznie lub wcale z każdą iteracją. Na przykład ta krzywa strat sugeruje zbieżność po około 700 iteracjach:
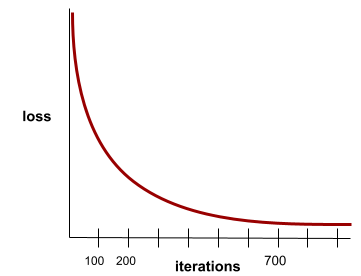
Model zbiega się, gdy dodatkowe trenowanie nie poprawia jego działania.
W uczeniu głębokim wartości funkcji straty czasami pozostają stałe lub prawie stałe przez wiele iteracji, zanim w końcu zaczną maleć. Podczas długiego okresu stałych wartości funkcji straty możesz tymczasowo odnieść fałszywe wrażenie zbieżności.
Zobacz też wczesne zatrzymanie.
Więcej informacji znajdziesz w sekcji Zbieżność modelu i krzywe utraty w kursie Machine Learning Crash Course.
kodowanie konwersacyjne,
Interaktywny dialog między Tobą a modelem generatywnej AI w celu tworzenia oprogramowania. Wydajesz prompt opisujący oprogramowanie. Następnie model używa tego opisu do wygenerowania kodu. Następnie wydajesz nowy prompt, aby wyeliminować wady poprzedniego promptu lub wygenerowanego kodu, a model generuje zaktualizowany kod. Będziecie się wymieniać informacjami, aż wygenerowane oprogramowanie będzie wystarczająco dobre.
Kodowanie konwersacji to w zasadzie pierwotne znaczenie kodowania nastroju.
Porównaj z kodowaniem specyfikacyjnym.
funkcja wypukła,
Funkcja, w której obszar nad wykresem funkcji jest zbiorem wypukłym. Typowa funkcja wypukła ma kształt litery U. Na przykład te funkcje są wypukłe:
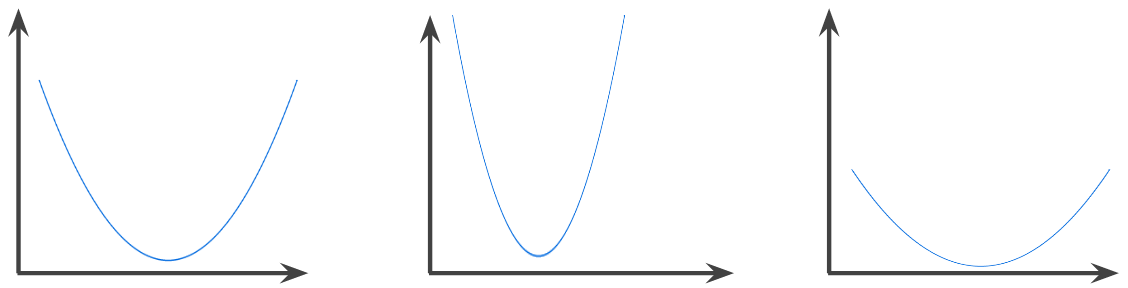
Natomiast ta funkcja nie jest wypukła. Zwróć uwagę, że obszar nad wykresem nie jest zbiorem wypukłym:

Funkcja ściśle wypukła ma dokładnie 1 lokalny punkt minimum, który jest też globalnym punktem minimum. Klasyczne funkcje w kształcie litery U są funkcjami ściśle wypukłymi. Niektóre funkcje wypukłe (np. linie proste) nie mają jednak kształtu litery U.
Więcej informacji znajdziesz w sekcji Zbieżność i funkcje wypukłe w kursie Machine Learning Crash Course.
optymalizacja wypukła,
Proces wykorzystywania technik matematycznych, takich jak metoda gradientu prostego, do znajdowania minimum funkcji wypukłej. Wiele badań nad uczeniem maszynowym koncentruje się na formułowaniu różnych problemów jako problemów optymalizacji wypukłej i na ich wydajniejszym rozwiązywaniu.
Szczegółowe informacje znajdziesz w książce Boyda i Vandenberghe Convex Optimization.
zbiór wypukły,
Podzbiór przestrzeni euklidesowej, w którym linia narysowana między dowolnymi dwoma punktami podzbioru pozostaje w całości w tym podzbiorze. Na przykład te 2 kształty są zbiorami wypukłymi:

Natomiast te 2 kształty nie są zbiorami wypukłymi:

splot
W matematyce, mówiąc potocznie, mieszanina dwóch funkcji. W uczeniu maszynowym operacja splotu łączy filtr splotowy i macierz wejściową, aby trenować wagi.
W uczeniu maszynowym termin „konwolucja” jest często skrótowym określeniem operacji konwolucyjnej lub warstwy konwolucyjnej.
Bez konwolucji algorytm uczenia maszynowego musiałby nauczyć się oddzielnej wagi dla każdej komórki w dużym tensorze. Na przykład algorytm uczenia maszynowego trenowany na obrazach o rozmiarze 2K x 2K musiałby znaleźć 4 mln oddzielnych wag. Dzięki konwolucjom algorytm uczenia maszynowego musi znaleźć wagi tylko dla każdej komórki filtra konwolucyjnego, co znacznie zmniejsza ilość pamięci potrzebnej do wytrenowania modelu. Gdy filtr konwolucyjny jest stosowany, jest on po prostu replikowany w komórkach, tak aby każda z nich była mnożona przez filtr.
Więcej informacji znajdziesz w wprowadzeniu do konwolucyjnych sieci neuronowych w kursie dotyczącym klasyfikacji obrazów.
filtr konwolucyjny,
Jeden z 2 elementów w operacji splotu. (Drugi aktor to wycinek macierzy wejściowej). Filtr konwolucyjny to macierz o takim samym rzędzie jak macierz wejściowa, ale o mniejszym kształcie. Na przykład w przypadku macierzy wejściowej 28 x 28 filtr może być dowolną macierzą 2D mniejszą niż 28 x 28.
W manipulacji fotograficznej wszystkie komórki filtra konwolucyjnego są zwykle ustawione na stały wzór jedynek i zer. W uczeniu maszynowym filtry konwolucyjne są zwykle inicjowane losowymi liczbami, a następnie sieć uczy się idealnych wartości.
Więcej informacji znajdziesz w sekcji Convolution w kursie Image Classification (Klasyfikacja obrazów).
warstwa konwolucyjna,
Warstwa głębokiej sieci neuronowej, w której filtr splotowy przekazuje macierz wejściową. Weźmy na przykład ten filtr konwolucyjny 3x3:
![Macierz 3x3 o wartościach: [[0,1,0], [1,0,1], [0,1,0]]](https://developers.google.cn/static/machine-learning/glossary/images/ConvolutionalFilter33.svg?authuser=00&hl=pl)
Poniższa animacja przedstawia warstwę konwolucyjną składającą się z 9 operacji konwolucyjnych obejmujących macierz wejściową 5x5. Zwróć uwagę, że każda operacja splotu działa na innym wycinku macierzy wejściowej o rozmiarach 3x3. Wynikowa macierz 3x3 (po prawej) składa się z wyników 9 operacji splotu:
![Animacja przedstawiająca 2 macierze. Pierwsza macierz to macierz 5x5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]].
Druga macierz to macierz 3x3:
[[181,303,618], [115,338,605], [169,351,560]].
Druga macierz jest obliczana przez zastosowanie filtra konwolucyjnego [[0, 1, 0], [1, 0, 1], [0, 1, 0]] do różnych podzbiorów 3x3 macierzy 5x5.](https://developers.google.cn/static/machine-learning/glossary/images/AnimatedConvolution.gif?authuser=00&hl=pl)
Więcej informacji znajdziesz w sekcji W pełni połączone warstwy w kursie Klasyfikacja obrazów.
konwolucyjna sieć neuronowa
Sieć neuronowa, w której co najmniej 1 warstwa jest warstwą konwolucyjną. Typowa konwolucyjna sieć neuronowa składa się z kombinacji tych warstw:
Splotowe sieci neuronowe osiągnęły duży sukces w przypadku niektórych rodzajów problemów, takich jak rozpoznawanie obrazów.
operacja splotu
Następujące dwuetapowe działanie matematyczne:
- Mnożenie elementów filtra konwolucyjnego i wycinka macierzy wejściowej. (Wycięty fragment macierzy wejściowej ma ten sam rząd i rozmiar co filtr konwolucyjny).
- Suma wszystkich wartości w wynikowej macierzy produktów.
Weźmy na przykład tę macierz wejściową 5x5:
![Macierz 5x5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]].](https://developers.google.cn/static/machine-learning/glossary/images/ConvolutionalLayerInputMatrix.svg?authuser=00&hl=pl)
Wyobraź sobie teraz ten filtr konwolucyjny 2x2:
![Macierz 2x2: [[1, 0], [0, 1]]](https://developers.google.cn/static/machine-learning/glossary/images/ConvolutionalLayerFilter.svg?authuser=00&hl=pl)
Każda operacja splotu obejmuje pojedynczy wycinek 2x2 macierzy wejściowej. Załóżmy na przykład, że używamy wycinka 2x2 w lewym górnym rogu macierzy wejściowej. Operacja splotu na tym wycinku wygląda tak:
![Zastosowanie filtra konwolucyjnego [[1, 0], [0, 1]] do lewego górnego fragmentu macierzy wejściowej o wymiarach 2x2, czyli [[128,97], [35,22]].
Filtr konwolucyjny pozostawia wartości 128 i 22 bez zmian, ale wyzerowuje wartości 97 i 35. W efekcie operacja splotu daje wartość 150 (128+22).](https://developers.google.cn/static/machine-learning/glossary/images/ConvolutionalLayerOperation.svg?authuser=00&hl=pl)
Warstwa konwolucyjna składa się z serii operacji konwolucyjnych, z których każda działa na innym wycinku macierzy wejściowej.
koszt
Synonim słowa strata.
wspólne szkolenie,
Podejście uczenia półnadzorowanego, które jest szczególnie przydatne, gdy spełnione są wszystkie te warunki:
- W zbiorze danych jest wysoki odsetek nieoznaczonych przykładów w porównaniu z oznaczonymi przykładami.
- Jest to problem klasyfikacji (binarnej lub wieloklasowej).
- Zbiór danych zawiera 2 różne zestawy cech predykcyjnych, które są od siebie niezależne i się uzupełniają.
Wspólne trenowanie wzmacnia niezależne sygnały, tworząc silniejszy sygnał. Rozważmy na przykład model klasyfikacji, który dzieli poszczególne używane samochody na dobre i złe. Jeden zestaw funkcji predykcyjnych może koncentrować się na ogólnych cechach, takich jak rok produkcji, marka i model samochodu, a inny zestaw może koncentrować się na historii jazdy poprzedniego właściciela i historii serwisowania samochodu.
Przełomowy artykuł na temat współtrenowania to Combining Labeled and Unlabeled Data with Co-Training autorstwa Bluma i Mitchella.
obiektywność kontrfaktyczna,
Miara sprawiedliwości, która sprawdza, czy model klasyfikacji daje ten sam wynik w przypadku 2 osób, z których jedna jest identyczna z drugą, z wyjątkiem co najmniej jednego atrybutu chronionego. Ocena modelu klasyfikacji pod kątem obiektywności kontrfaktycznej to jedna z metod wykrywania potencjalnych źródeł uprzedzeń w modelu.
Więcej informacji znajdziesz w tych artykułach:
- Sprawiedliwość: sprawiedliwość kontrfaktyczna w szybkim szkoleniu z uczenia maszynowego.
- When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness
błąd pokrycia,
Zobacz błąd doboru.
crash blossom
Zdanie lub wyrażenie o niejednoznacznym znaczeniu. Crash blossoms stanowią poważny problem w rozumieniu języka naturalnego. Na przykład nagłówek Red Tape Holds Up Skyscraper (Biurokracja wstrzymuje budowę wieżowca) jest przykładem crash blossom, ponieważ model NLU może zinterpretować go dosłownie lub w przenośni.
krytyk,
Synonim sieci Deep Q.
entropia krzyżowa
Uogólnienie funkcji straty logarytmicznej na problemy z klasyfikacją wieloklasową. Entropia krzyżowa określa różnicę między dwoma rozkładami prawdopodobieństwa. Zobacz też perplexity.
walidacja krzyżowa,
Mechanizm szacowania, jak dobrze model uogólni się na nowe dane, poprzez testowanie go na co najmniej 1 niepokrywającym się podzbiorze danych wyłączonym ze zbioru treningowego.
dystrybuanta
Funkcja, która określa częstotliwość próbek mniejszą lub równą wartości docelowej. Rozważmy na przykład rozkład normalny wartości ciągłych. Dystrybuanta informuje, że około 50% próbek powinno być mniejszych lub równych średniej, a około 84% próbek powinno być mniejszych lub równych odchyleniu standardowemu powyżej średniej.
D
analiza danych,
Zrozumienie danych przez analizowanie próbek, pomiarów i wizualizacji. Analiza danych może być szczególnie przydatna po pierwszym otrzymaniu zbioru danych, zanim utworzysz pierwszy model. Jest to również kluczowe w przypadku eksperymentów i rozwiązywania problemów z systemem.
augmentacja danych,
Sztuczne zwiększanie zakresu i liczby przykładów treningowych przez przekształcanie dotychczasowych przykładów w celu tworzenia dodatkowych przykładów. Załóżmy na przykład, że obrazy są jedną z Twoich funkcji, ale zbiór danych nie zawiera wystarczającej liczby przykładów obrazów, aby model mógł nauczyć się przydatnych powiązań. Najlepiej dodać do zbioru danych wystarczającą liczbę oznaczonych etykietami obrazów, aby umożliwić prawidłowe trenowanie modelu. Jeśli nie jest to możliwe, rozszerzanie danych może obracać, rozciągać i odzwierciedlać każdy obraz, aby uzyskać wiele wariantów oryginalnego zdjęcia, co może zapewnić wystarczającą ilość oznaczonych danych do przeprowadzenia skutecznego trenowania.
[struktura] DataFrame
Popularny typ danych pandas do reprezentowania zbiorów danych w pamięci.
DataFrame jest podobny do tabeli lub arkusza kalkulacyjnego. Każda kolumna obiektu DataFrame ma nazwę (nagłówek), a każdy wiersz jest identyfikowany przez unikalny numer.
Każda kolumna w obiekcie DataFrame jest uporządkowana jak tablica dwuwymiarowa, z tym wyjątkiem, że każdej kolumnie można przypisać własny typ danych.
Zapoznaj się też z oficjalną stroną referencyjną pandas.DataFrame.
równoległość danych,
Sposób skalowania trenowania lub wnioskowania, który polega na replikowaniu całego modelu na wielu urządzeniach, a następnie przekazywaniu do każdego z nich podzbioru danych wejściowych. Równoległość danych może umożliwić trenowanie i wnioskowanie przy bardzo dużych rozmiarach partii. Wymaga jednak, aby model był wystarczająco mały, aby zmieścił się na wszystkich urządzeniach.
Równoległość danych zwykle przyspiesza trenowanie i wnioskowanie.
Zobacz też równoległość modelu.
Dataset API (tf.data)
Interfejs API TensorFlow wysokiego poziomu do odczytywania danych i przekształcania ich w formę wymaganą przez algorytm uczenia maszynowego.
Obiekt tf.data.Dataset reprezentuje sekwencję elementów, w której każdy element zawiera co najmniej 1 tensor. Obiekt tf.data.Iterator
umożliwia dostęp do elementów Dataset.
zbiór danych
Zbiór surowych danych, zwykle (ale nie tylko) zorganizowanych w jednym z tych formatów:
- arkusz kalkulacyjny,
- plik w formacie CSV (wartości rozdzielane przecinkami);
granica decyzyjna,
Separator między klasami wyuczonymi przez model w problemach z klasyfikacją binarną lub wieloklasową. Na przykład na poniższym obrazie przedstawiającym problem klasyfikacji binarnej granica decyzyjna to linia między klasą pomarańczową a klasą niebieską:

las decyzyjny,
Model utworzony z wielu drzew decyzyjnych. Las decyzyjny tworzy prognozę, agregując prognozy drzew decyzyjnych. Popularne rodzaje lasów decyzyjnych to lasy losowe i drzewa wzmocnione gradientowo.
Więcej informacji znajdziesz w sekcji Lasy decyzyjne w kursie Lasy decyzyjne.
próg decyzji
Synonim terminu próg klasyfikacji.
drzewo decyzyjne,
Nadzorowany model systemów uczących się składający się z zestawu warunków i węzłów końcowych uporządkowanych hierarchicznie. Oto przykład drzewa decyzyjnego:
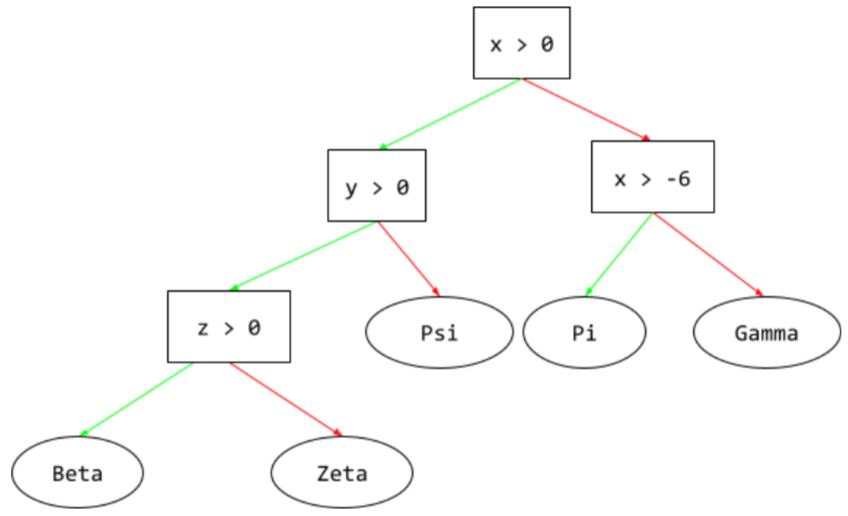
dekoder,
Ogólnie rzecz biorąc, każdy system ML, który przekształca przetworzoną, gęstą lub wewnętrzną reprezentację w bardziej surową, rzadką lub zewnętrzną reprezentację.
Dekodery są często elementem większego modelu, w którym są zwykle połączone z enkoderem.
W zadaniach typu sekwencja na sekwencję dekoder zaczyna od stanu wewnętrznego wygenerowanego przez enkoder, aby przewidzieć następną sekwencję.
Definicję dekodera w architekturze transformatora znajdziesz w sekcji Transformer.
Więcej informacji znajdziesz w sekcji Duże modele językowe w szybkim szkoleniu z uczenia maszynowego.
model głęboki,
Sieć neuronowa zawierająca więcej niż jedną warstwę ukrytą.
Model głęboki jest też nazywany głęboką siecią neuronową.
Kontrast z modelem szerokim.
głęboka sieć neuronowa
Synonim terminu model głęboki.
Sieć Deep Q (DQN)
W Q-learningu głęboka sieć neuronowa, która prognozuje funkcje Q.
Krytyk to synonim sieci Deep Q-Network.
parytet demograficzny
Metryka sprawiedliwości, która jest spełniona, jeśli wyniki klasyfikacji modelu nie zależą od danego atrybutu wrażliwego.
Jeśli na przykład zarówno Liliputanie, jak i Brobdingnagianie ubiegają się o przyjęcie na Uniwersytet Glubbdubdrib, równość demograficzna jest osiągana, gdy odsetek przyjętych Liliputanów jest taki sam jak odsetek przyjętych Brobdingnagian, niezależnie od tego, czy jedna grupa jest średnio bardziej wykwalifikowana od drugiej.
Kontrastuje to z wyrównanymi szansami i równością szans, które dopuszczają, aby wyniki klasyfikacji w agregacji zależały od atrybutów wrażliwych, ale nie dopuszczają, aby wyniki klasyfikacji dla określonych etykiet prawdziwych danych zależały od atrybutów wrażliwych. Więcej informacji znajdziesz w artykule „Walka z dyskryminacją za pomocą inteligentniejszych systemów uczących się”, w którym znajdziesz wizualizację przedstawiającą kompromisy przy optymalizacji pod kątem równości demograficznej.
Więcej informacji znajdziesz w sekcji Sprawiedliwość: równość demograficzna w szybkim szkoleniu z uczenia maszynowego.
odszumianie,
Powszechne podejście do samodzielnego uczenia się, w którym:
Usuwanie szumu umożliwia uczenie się na nieoznaczonych przykładach. Oryginalny zbiór danych służy jako cel lub etykieta, a zaszumione dane jako dane wejściowe.
Niektóre zamaskowane modele językowe wykorzystują odszumianie w ten sposób:
- Do nieoznaczonego zdania sztucznie dodawany jest szum przez zamaskowanie niektórych tokenów.
- Model próbuje przewidzieć oryginalne tokeny.
gęsta cecha,
Cechą, w której większość lub wszystkie wartości są niezerowe, jest zwykle tensor wartości zmiennoprzecinkowych. Na przykład ten 10-elementowy tensor jest gęsty, ponieważ 9 jego wartości jest niezerowych:
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
Kontrast z rzadką cechą.
warstwa gęsta,
Synonim w pełni połączonej warstwy.
głębokość
Suma tych elementów w sieci neuronowej:
- liczba warstw ukrytych,
- liczba warstw wyjściowych, która zwykle wynosi 1,
- liczba warstw wektorów dystrybucyjnych;
Na przykład sieć neuronowa z 5 warstwami ukrytymi i 1 warstwą wyjściową ma głębokość 6.
Zwróć uwagę, że warstwa wejściowa nie wpływa na głębokość.
głęboka sieć neuronowa z splotem separowalnym (sepCNN),
Architektura konwolucyjnej sieci neuronowej oparta na architekturze Inception, w której moduły Inception zostały zastąpione konwolucjami separowalnymi głębokościowo. Inna nazwa to Xception.
Konwolucja separowalna głębokościowo (zwana też konwolucją separowalną) rozkłada standardową konwolucję 3D na 2 oddzielne operacje konwolucji, które są bardziej wydajne obliczeniowo: najpierw konwolucję głębokościową o głębokości 1 (n × n × 1), a potem konwolucję punktową o długości i szerokości 1 (1 × 1 × n).
Więcej informacji znajdziesz w artykule Xception: Deep Learning with Depthwise Separable Convolutions.
etykieta pochodna
Synonim etykiety proxy.
urządzenie
Przeciążony termin o 2 możliwych definicjach:
- Kategoria sprzętu, na którym można uruchomić sesję TensorFlow, w tym procesory CPU, GPU i TPU.
- Podczas trenowania modelu uczenia maszynowego na akceleratorach (procesorach GPU lub TPU) część systemu, która faktycznie przetwarza tensory i wektory. Urządzenie działa na chipach akceleratora. Natomiast host zwykle działa na procesorze.
prywatność różnicowa,
W uczeniu maszynowym jest to metoda anonimizacji, która chroni wszelkie dane wrażliwe (np. dane osobowe) zawarte w zbiorze treningowym modelu przed ujawnieniem. Dzięki temu model nie uczy się ani nie zapamiętuje zbyt wielu informacji o konkretnej osobie. Osiąga się to przez próbkowanie i dodawanie szumu podczas trenowania modelu, aby zacierać poszczególne punkty danych, co zmniejsza ryzyko ujawnienia wrażliwych danych treningowych.
Prywatność różnicowa jest też używana poza uczeniem maszynowym. Na przykład analitycy danych czasami używają prywatności różnicowej, aby chronić prywatność poszczególnych osób podczas obliczania statystyk korzystania z usługi w przypadku różnych grup demograficznych.
redukcja wymiarów,
Zmniejszenie liczby wymiarów używanych do reprezentowania konkretnej cechy w wektorze cech, zwykle przez przekształcenie go w wektor dystrybucyjny.
wymiary
Przeciążony termin o jednej z tych definicji:
Liczba poziomów współrzędnych w Tensor. Przykład:
- Skalar ma 0 wymiarów, np.
["Hello"]. - Wektor ma jeden wymiar, np.
[3, 5, 7, 11]. - Macierz ma 2 wymiary, np.
[[2, 4, 18], [5, 7, 14]]. Aby jednoznacznie określić konkretną komórkę w wektorze jednowymiarowym, potrzebujesz 1 współrzędnej. Aby jednoznacznie określić konkretną komórkę w macierzy dwuwymiarowej, potrzebujesz 2 współrzędnych.
- Skalar ma 0 wymiarów, np.
Liczba wpisów w wektorze cech.
Liczba elementów w warstwie osadzania.
bezpośrednie prompty
Synonim promptów „zero-shot”.
cecha dyskretna,
Cechę z skończonym zbiorem możliwych wartości. Na przykład cecha, której wartości mogą być tylko zwierzę, roślina lub minerał, jest cechą dyskretną (lub kategorialną).
Kontrast z cechą ciągłą.
model dyskryminacyjny
Model, który prognozuje etykiety na podstawie zestawu co najmniej 1 cechy. Bardziej formalnie, modele dyskryminacyjne definiują rozkład warunkowy wartości wyjściowej na podstawie cech i wag, czyli:
p(output | features, weights)
Na przykład model, który na podstawie cech i wag przewiduje, czy e-mail jest spamem, jest modelem dyskryminatywnym.
Zdecydowana większość modeli uczenia nadzorowanego, w tym modele klasyfikacji i regresji, to modele dyskryminatywne.
W przeciwieństwie do modelu generatywnego.
dyskryminator,
System, który określa, czy przykłady są prawdziwe czy fałszywe.
Alternatywnie jest to podsystem w generatywnej sieci przeciwstawnej, który określa, czy przykłady utworzone przez generator są prawdziwe czy fałszywe.
Więcej informacji znajdziesz w sekcji dotyczącej dyskryminatora w kursie na temat sieci GAN.
nieproporcjonalny wpływ,
podejmowanie decyzji dotyczących osób, które w nieproporcjonalny sposób wpływają na różne podgrupy populacji; Zwykle odnosi się to do sytuacji, w których proces podejmowania decyzji przez algorytm przynosi szkodę lub korzyść niektórym podgrupom bardziej niż innym.
Załóżmy na przykład, że algorytm określający, czy mieszkaniec Lilipucji kwalifikuje się do otrzymania kredytu na miniaturowy dom, częściej klasyfikuje go jako „niekwalifikującego się”, jeśli jego adres pocztowy zawiera określony kod pocztowy. Jeśli mieszkańcy Lilipucji, którzy otwierają jajka od większego końca, częściej mają adresy pocztowe z tym kodem pocztowym niż mieszkańcy Lilipucji, którzy otwierają jajka od mniejszego końca, ten algorytm może mieć nieproporcjonalny wpływ.
Kontrastuje to z nierównym traktowaniem, które koncentruje się na różnicach wynikających z tego, że charakterystyki podgrup są jawnymi danymi wejściowymi w procesie podejmowania decyzji przez algorytm.
nierówne traktowanie,
Uwzględnianie atrybutów wrażliwych osób, których dotyczą dane, w procesie podejmowania decyzji przez algorytm w taki sposób, że różne podgrupy osób są traktowane odmiennie.
Rozważmy na przykład algorytm, który określa, czy Liliputanie kwalifikują się do otrzymania pożyczki na miniaturowy dom na podstawie danych podanych we wniosku o pożyczkę. Jeśli algorytm wykorzystuje przynależność do Lilliputian jako Big-Endian lub Little-Endian jako dane wejściowe, stosuje nierówne traktowanie w tym wymiarze.
Kontrastuje to z nieproporcjonalnym wpływem, który koncentruje się na różnicach w społecznym wpływie decyzji algorytmicznych na podgrupy, niezależnie od tego, czy te podgrupy są danymi wejściowymi modelu.
destylacja,
Proces zmniejszania rozmiaru jednego modelu (zwanego modelem nauczycielskim) do mniejszego modelu (zwanego modelem uczniowskim), który jak najwierniej naśladuje prognozy modelu oryginalnego. Destylacja jest przydatna, ponieważ mniejszy model ma 2 główne zalety w porównaniu z większym modelem (nauczycielem):
- Szybszy czas wnioskowania
- mniejsze zużycie pamięci i energii,
Prognozy ucznia zwykle nie są jednak tak dobre jak prognozy nauczyciela.
Destylacja trenuje model ucznia, aby zminimalizować funkcję straty na podstawie różnicy między wynikami prognoz modeli ucznia i nauczyciela.
Porównaj destylację z tymi pojęciami:
Więcej informacji znajdziesz w szybkim szkoleniu z uczenia maszynowego w sekcji LLM: dostrajanie, destylacja i inżynieria promptów.
distribution
Częstotliwość i zakres różnych wartości dla danego atrybutu lub etykiety. Rozkład określa prawdopodobieństwo wystąpienia danej wartości.
Obraz poniżej przedstawia histogramy 2 różnych rozkładów:
- Po lewej stronie rozkład potęgowy bogactwa w zależności od liczby osób posiadających to bogactwo.
- Po prawej stronie znajduje się rozkład normalny wzrostu w porównaniu z liczbą osób o danym wzroście.
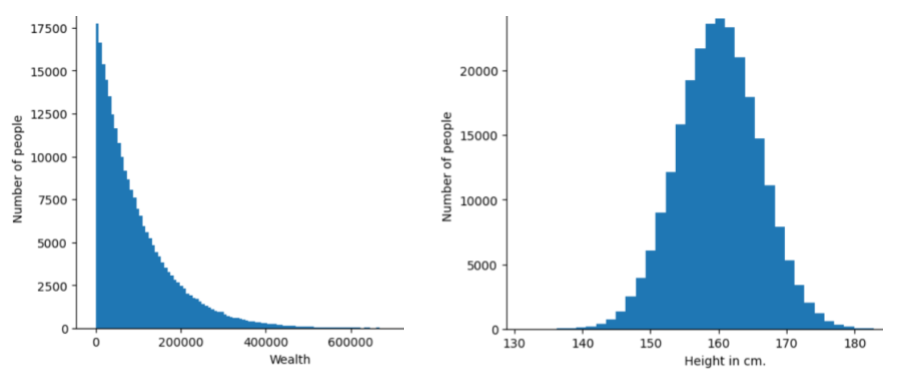
Poznanie rozkładu każdej cechy i etykiety może pomóc w określeniu, jak normalizować wartości i wykrywać wartości odstające.
Określenie poza rozkładem odnosi się do wartości, która nie występuje w zbiorze danych lub jest bardzo rzadka. Na przykład obraz planety Saturn będzie uznawany za wykraczający poza zakres zbioru danych składającego się z obrazów kotów.
grupowanie rozdzielne,
Zobacz klastrowanie hierarchiczne.
zmniejszanie liczby próbek
Termin o wielu znaczeniach, który może oznaczać:
- Zmniejszanie ilości informacji w cechach, aby trenować model wydajniej. Na przykład przed wytrenowaniem modelu rozpoznawania obrazów zmniejsz rozdzielczość obrazów o wysokiej rozdzielczości do formatu o niższej rozdzielczości.
- Trenowanie na nieproporcjonalnie niskim odsetku nadreprezentowanych przykładów klasy w celu poprawy trenowania modelu na niedoreprezentowanych klasach. Na przykład w przypadku zbioru danych z nierównowagą klas modele zwykle uczą się dużo o klasie większościowej, a za mało o klasie mniejszościowej. Downsampling pomaga zrównoważyć ilość trenowania w przypadku klas większościowych i mniejszościowych.
Więcej informacji znajdziesz w sekcji Zbiory danych: niezrównoważone zbiory danych w szybkim szkoleniu z uczenia maszynowego.
DQN
Skrót od Deep Q-Network.
regularyzacja przez wyłączanie
Forma regularyzacji przydatna w trenowaniu sieci neuronowych. Regularyzacja przez wyłączanie usuwa losowo wybraną stałą liczbę jednostek w warstwie sieci w przypadku pojedynczego kroku gradientu. Im więcej jednostek zostanie wyłączonych, tym silniejsza będzie regularyzacja. Jest to analogiczne do trenowania sieci w celu emulowania wykładniczo dużej ensemblu mniejszych sieci. Więcej informacji znajdziesz w artykule Dropout: A Simple Way to Prevent Neural Networks from Overfitting.
dynamiczny
Czynność wykonywana często lub w sposób ciągły. W kontekście uczenia maszynowego terminy dynamiczny i online są synonimami. Oto typowe zastosowania terminów dynamiczny i online w uczeniu maszynowym:
- Model dynamiczny (lub model online) to model, który jest często lub stale ponownie trenowany.
- Szkolenie dynamiczne (lub szkolenie online) to proces szkolenia przeprowadzany często lub w sposób ciągły.
- Wnioskowanie dynamiczne (lub wnioskowanie online) to proces generowania prognoz na żądanie.
model dynamiczny,
Model, który jest często (a nawet ciągle) ponownie trenowany. Model dynamiczny to „uczeń przez całe życie”, który stale dostosowuje się do zmieniających się danych. Model dynamiczny jest też nazywany modelem online.
Kontrast z modelem statycznym.
E
wykonanie natychmiastowe,
Środowisko programowania TensorFlow, w którym operacje są wykonywane natychmiast. Z kolei operacje wywoływane w ramach wykonywania grafu nie są uruchamiane, dopóki nie zostaną jawnie obliczone. Wykonanie natychmiastowe to interfejs imperatywny, podobny do kodu w większości języków programowania. Programy z wykonywaniem natychmiastowym są zwykle znacznie łatwiejsze do debugowania niż programy z wykonywaniem grafu.
wczesne zatrzymanie,
Metoda regularyzacji polegająca na zakończeniu trenowania zanim strata trenowania przestanie maleć. W przypadku wczesnego zatrzymania celowo przerywasz trenowanie modelu, gdy strata w zbiorze danych weryfikacyjnych zaczyna rosnąć, czyli gdy pogarsza się skuteczność uogólniania.
Kontrastuje z wcześniejszym wyjściem.
odległość przeniesienia ziemi (EMD),
Miara względnego podobieństwa dwóch rozkładów. Im mniejsza odległość między rozkładami, tym są one bardziej podobne.
odległość edycji,
Miara podobieństwa dwóch ciągów tekstowych. W uczeniu maszynowym odległość edycji jest przydatna z tych powodów:
- Odległość edycji jest łatwa do obliczenia.
- Odległość edycji może porównywać dwa ciągi, o których wiadomo, że są do siebie podobne.
- Odległość edycji może określać stopień podobieństwa różnych ciągów znaków do danego ciągu.
Istnieje kilka definicji odległości edycji, z których każda wykorzystuje inne operacje na ciągach znaków. Przykład znajdziesz w artykule Odległość Levenshteina.
Notacja Einsum
Skuteczna notacja opisująca sposób łączenia 2 tensorów. Tensory są łączone przez pomnożenie elementów jednego tensora przez elementy drugiego tensora, a następnie zsumowanie iloczynów. Notacja Einsum używa symboli do identyfikowania osi każdego tensora, a te same symbole są przestawiane w celu określenia kształtu nowego tensora wynikowego.
NumPy udostępnia typową implementację funkcji Einsum.
warstwa wektora dystrybucyjnego
Specjalna warstwa ukryta, która trenuje na podstawie wielowymiarowej cechy kategorycznej, aby stopniowo uczyć się wektora dystrybucyjnego o mniejszej liczbie wymiarów. Warstwa wektorów dystrybucyjnych umożliwia sieci neuronowej znacznie wydajniejsze trenowanie niż w przypadku trenowania tylko na podstawie wielowymiarowej cechy kategorialnej.
Na przykład Earth obsługuje obecnie około 73 tys. gatunków drzew. Załóżmy, że gatunek drzewa jest cechą w Twoim modelu,więc warstwa wejściowa modelu zawiera wektor kodowania 1-z-N o długości 73 000 elementów.
Na przykład znak baobab może być reprezentowany w ten sposób:

Tablica zawierająca 73 tys. elementów jest bardzo długa. Jeśli nie dodasz do modelu warstwy osadzania, trenowanie będzie bardzo czasochłonne ze względu na mnożenie 72 999 zer. Załóżmy, że wybierzesz warstwę wektorów dystrybucyjnych składającą się z 12 wymiarów. W rezultacie warstwa osadzania będzie stopniowo uczyć się nowego wektora osadzania dla każdego gatunku drzewa.
W niektórych sytuacjach haszowanie jest rozsądną alternatywą dla warstwy osadzania.
Więcej informacji znajdziesz w sekcji Osadzanie w Szybkim szkoleniu z uczenia maszynowego.
przestrzeń wektorów dystrybucyjnych,
d-wymiarowa przestrzeń wektorowa, do której są mapowane cechy z przestrzeni wektorowej o większej liczbie wymiarów. Przestrzeń wektorów dystrybucyjnych jest trenowana w taki sposób, aby wychwytywać strukturę, która jest istotna dla docelowej aplikacji.
Iloczyn skalarny 2 wektorów dystrybucyjnych jest miarą ich podobieństwa.
wektor dystrybucyjny
Ogólnie rzecz biorąc, jest to tablica liczb zmiennoprzecinkowych pochodzących z dowolnej warstwy ukrytej, która opisuje dane wejściowe tej warstwy. Wektor dystrybucyjny to często tablica liczb zmiennoprzecinkowych wytrenowana w warstwie wektorów dystrybucyjnych. Załóżmy na przykład, że warstwa wektorów dystrybucyjnych musi nauczyć się wektora dystrybucyjnego dla każdego z 73 tys. gatunków drzew na Ziemi. Załóżmy, że poniższa tablica jest wektorem reprezentacji właściwościowych baobabu:

Wektor dystrybucyjny to nie zbiór losowych liczb. Warstwa osadzania określa te wartości podczas trenowania, podobnie jak sieć neuronowa uczy się innych wag podczas trenowania. Każdy element tablicy to ocena dotycząca pewnej cechy gatunku drzewa. Który element reprezentuje cechy którego gatunku drzewa? Jest to bardzo trudne do określenia dla ludzi.
Matematycznie istotną cechą wektora dystrybucyjnego jest to, że podobne elementy mają podobne zestawy liczb zmiennoprzecinkowych. Na przykład podobne gatunki drzew mają bardziej zbliżony zestaw liczb zmiennoprzecinkowych niż gatunki drzew, które nie są do siebie podobne. Sekwoje i mamutowce to spokrewnione gatunki drzew, więc będą miały bardziej podobny zestaw liczb zmiennoprzecinkowych niż sekwoje i palmy kokosowe. Liczby w wektorze osadzania będą się zmieniać za każdym razem, gdy ponownie wytrenujesz model, nawet jeśli użyjesz identycznych danych wejściowych.
empiryczna dystrybuanta (eCDF lub EDF)
Dystrybuanta na podstawie pomiarów empirycznych z rzeczywistego zbioru danych. Wartość funkcji w dowolnym punkcie osi X to ułamek obserwacji w zbiorze danych, które są mniejsze lub równe określonej wartości.
minimalizacja ryzyka empirycznego (ERM),
wybór funkcji, która minimalizuje stratę w zbiorze treningowym; Porównaj z minimalizacją ryzyka strukturalnego.
koder
Ogólnie rzecz biorąc, każdy system ML, który przekształca surowe, rzadkie lub zewnętrzne dane wejściowe w bardziej przetworzone, gęstsze lub wewnętrzne dane wyjściowe.
Enkodery są często elementem większego modelu, w którym są zwykle połączone z dekoderem. Niektóre transformatory łączą kodery z dekoderami, ale inne transformatory używają tylko kodera lub tylko dekodera.
Niektóre systemy używają danych wyjściowych enkodera jako danych wejściowych do sieci klasyfikacyjnej lub regresyjnej.
W zadaniach typu sekwencja na sekwencję enkoder przyjmuje sekwencję wejściową i zwraca stan wewnętrzny (wektor). Następnie dekoder używa tego stanu wewnętrznego do przewidywania następnej sekwencji.
Definicję enkodera w architekturze transformatora znajdziesz w sekcji Transformator.
Więcej informacji znajdziesz w module LLM: co to jest duży model językowy w szybkim szkoleniu z systemów uczących się.
punkty końcowe
Lokalizacja dostępna w sieci (zwykle adres URL), w której można uzyskać dostęp do usługi.
ensemble
Zbiór modeli wytrenowanych niezależnie, których prognozy są uśredniane lub agregowane. W wielu przypadkach zespół modeli daje lepsze prognozy niż pojedynczy model. Na przykład las losowy to zespół zbudowany z wielu drzew decyzyjnych. Pamiętaj, że nie wszystkie lasy decyzyjne są zespołami.
Więcej informacji znajdziesz w sekcji Las losowy w szybkim szkoleniu z uczenia maszynowego.
entropia
W teorii informacji jest to opis tego, jak nieprzewidywalny jest rozkład prawdopodobieństwa. Entropia jest też definiowana jako ilość informacji zawartych w każdym przykładzie. Rozkład ma najwyższą możliwą entropię, gdy wszystkie wartości zmiennej losowej są jednakowo prawdopodobne.
Entropia zbioru z 2 możliwymi wartościami „0” i „1” (np. etykietami w problemie klasyfikacji binarnej) ma następujący wzór:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
gdzie:
- H to entropia.
- p to ułamek przykładów „1”.
- q to ułamek przykładów „0”. Pamiętaj, że q = (1 – p).
- log to zwykle log2. W tym przypadku jednostką entropii jest bit.
Załóżmy na przykład, że:
- 100 przykładów zawiera wartość „1”
- 300 przykładów zawiera wartość „0”
Wartość entropii wynosi więc:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) - (0,75)log2(0,75) = 0,81 bita na przykład
Zbiór, który jest doskonale zrównoważony (np.200 zer i 200 jedynek), ma entropię 1,0 bita na przykład. W miarę jak zbiór staje się bardziej niezrównoważony, jego entropia zbliża się do 0,0.
W drzewach decyzyjnych entropia pomaga formułować przyrost informacji, aby rozdzielacz mógł wybierać warunki podczas tworzenia drzewa decyzyjnego klasyfikacji.
Porównaj entropię z:
- zanieczyszczenie Giniego
- funkcja straty entropii krzyżowej,
Entropia jest często nazywana entropią Shannona.
Więcej informacji znajdziesz w sekcji Exact splitter for binary classification with numerical features (Dokładny rozdzielacz do klasyfikacji binarnej z cechami numerycznymi) w kursie Decision Forests.
środowisko
W uczeniu ze wzmocnieniem świat, w którym znajduje się agent i który umożliwia mu obserwowanie stanu tego świata. Może to być np. świat gry, takiej jak szachy, lub świat fizyczny, np. labirynt. Gdy agent zastosuje działanie w środowisku, środowisko przechodzi między stanami.
odcinek
W uczeniu ze wzmocnieniem każda z powtarzanych prób agenta nauczenia się środowiska.
początek epoki : epoka
Pełne przejście treningowe przez cały zbiór treningowy, w którym każdy przykład został przetworzony raz.
Epoka to N/rozmiar wsadu iteracji trenowania, gdzie N to całkowita liczba przykładów.
Załóżmy na przykład, że:
- Zbiór danych składa się z 1000 przykładów.
- Rozmiar wsadu to 50 przykładów.
Dlatego jedna epoka wymaga 20 iteracji:
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
zasada zachłanna epsilon
W uczeniu ze wzmocnieniem zasada, która z prawdopodobieństwem epsilon stosuje zasadę losową, a w pozostałych przypadkach zasadę zachłanną. Jeśli np.wartość epsilona wynosi 0,9, zasady są losowe w 90% przypadków, a w 10% przypadków są zachłanne.
W kolejnych epizodach algorytm zmniejsza wartość epsilona, aby przejść od stosowania losowej strategii do stosowania strategii zachłannej. Dzięki zmianie strategii agent najpierw losowo eksploruje środowisko, a potem zachłannie wykorzystuje wyniki losowej eksploracji.
równość szans,
Wskaźnik sprawiedliwości, który pozwala ocenić, czy model prognozuje pożądany wynik równie dobrze dla wszystkich wartości wrażliwego atrybutu. Inaczej mówiąc, jeśli pożądanym wynikiem modelu jest klasa pozytywna, celem jest uzyskanie takiej samej liczby prawdziwie pozytywnych wyników dla wszystkich grup.
Równość szans jest związana z wyrównaniem szans, co wymaga, aby zarówno współczynniki wyników prawdziwie pozytywnych, jak i współczynniki wyników fałszywie pozytywnych były takie same dla wszystkich grup.
Załóżmy, że Uniwersytet Glubbdubdrib przyjmuje do wymagającego programu matematycznego zarówno Liliputów, jak i Brobdingnagów. Szkoły średnie w Lillipucie oferują rozbudowany program nauczania matematyki, a większość uczniów kwalifikuje się do programu uniwersyteckiego. W szkołach średnich Brobdingnagian nie ma zajęć z matematyki, w związku z czym znacznie mniej uczniów ma odpowiednie kwalifikacje. Równość szans jest zachowana w przypadku preferowanej etykiety „przyjęty” w odniesieniu do narodowości (Liliput lub Brobdingnag), jeśli kwalifikujący się uczniowie mają takie samo prawdopodobieństwo przyjęcia niezależnie od tego, czy są Liliputami, czy Brobdingnagami.
Załóżmy na przykład, że na Uniwersytet Glubbdubdrib zgłasza się 100 Liliputów i 100 Brobdingnagów, a decyzje o przyjęciu są podejmowane w ten sposób:
Tabela 1. Kandydaci z Lilliput (90% z nich spełnia wymagania)
| Zakwalifikowany | Niezakwalifikowany | |
|---|---|---|
| Przyjęto | 45 | 3 |
| Odrzucono | 45 | 7 |
| Łącznie | 90 | 10 |
|
Odsetek przyjętych uczniów spełniających kryteria: 45/90 = 50% Odsetek odrzuconych uczniów niespełniających kryteriów: 7/10 = 70% Łączny odsetek przyjętych uczniów z Lilliputu: (45+3)/100 = 48% |
||
Tabela 2. Kandydaci z Brobdingnagu (10% – kwalifikujący się):
| Zakwalifikowany | Niezakwalifikowany | |
|---|---|---|
| Przyjęto | 5 | 9 |
| Odrzucono | 5 | 81 |
| Łącznie | 10 | 90 |
|
Odsetek przyjętych uczniów spełniających kryteria: 5/10 = 50% Odsetek odrzuconych uczniów niespełniających kryteriów: 81/90 = 90% Łączny odsetek przyjętych uczniów z Brobdingnagu: (5+9)/100 = 14% |
||
Powyższe przykłady spełniają warunek równości szans w przypadku przyjęcia wykwalifikowanych uczniów, ponieważ wykwalifikowani Liliputanie i Brobdingnagianie mają 50% szans na przyjęcie.
Chociaż równość szans jest spełniona, te 2 kryteria obiektywności nie są spełnione:
- parytet demograficzny: Liliputanie i Brobdingnagianie są przyjmowani na uniwersytet w różnym tempie; 48% uczniów z Liliputu jest przyjmowanych, ale tylko 14% uczniów z Brobdingnagu.
- Równe szanse: chociaż kwalifikujący się uczniowie z Lilliputu i Brobdingnagu mają takie same szanse na przyjęcie, dodatkowe ograniczenie, że niekwalifikujący się uczniowie z Lilliputu i Brobdingnagu mają takie same szanse na odrzucenie, nie jest spełnione. W przypadku osób niekwalifikujących się do kategorii Liliputów odsetek odrzuceń wynosi 70%, a w przypadku osób niekwalifikujących się do kategorii Brobdingnagów – 90%.
Więcej informacji znajdziesz w sekcji Sprawiedliwość: równość szans w Szybkim szkoleniu z uczenia maszynowego.
wyrównane szanse
Wskaźnik sprawiedliwości, który pozwala ocenić, czy model prognozuje wyniki równie dobrze dla wszystkich wartości wrażliwego atrybutu w odniesieniu do klasy pozytywnej i klasy negatywnej, a nie tylko jednej z nich. Innymi słowy, zarówno współczynnik wyników prawdziwie dodatnich, jak i współczynnik wyników fałszywie ujemnych powinny być takie same w przypadku wszystkich grup.
Wyrównane szanse są powiązane z równością szans, która koncentruje się tylko na odsetku błędów w przypadku jednej klasy (pozytywnej lub negatywnej).
Załóżmy na przykład, że Uniwersytet Glubbdubdrib przyjmuje do wymagającego programu matematycznego zarówno Liliputów, jak i Brobdingnagów. Szkoły średnie w Lilliput oferują bogaty program nauczania matematyki, a większość uczniów kwalifikuje się do programu uniwersyteckiego. W szkołach średnich w Brobdingnagu nie ma zajęć z matematyki, więc znacznie mniej uczniów ma odpowiednie kwalifikacje. Warunek wyrównanych szans jest spełniony, jeśli niezależnie od tego, czy kandydat jest Liliputem, czy Brobdingnagiem, jeśli ma odpowiednie kwalifikacje, ma takie samo prawdopodobieństwo przyjęcia do programu, a jeśli nie ma odpowiednich kwalifikacji, ma takie samo prawdopodobieństwo odrzucenia.
Załóżmy, że na Uniwersytet Glubbdubdrib zgłasza się 100 Liliputów i 100 Brobdingnagów, a decyzje o przyjęciu są podejmowane w ten sposób:
Tabela 3. Kandydaci z Lilliput (90% z nich spełnia wymagania)
| Zakwalifikowany | Niezakwalifikowany | |
|---|---|---|
| Przyjęto | 45 | 2 |
| Odrzucono | 45 | 8 |
| Łącznie | 90 | 10 |
|
Odsetek przyjętych uczniów spełniających kryteria: 45/90 = 50% Odsetek odrzuconych uczniów niespełniających kryteriów: 8/10 = 80% Łączny odsetek przyjętych uczniów z Lilliputu: (45+2)/100 = 47% |
||
Tabela 4. Kandydaci z Brobdingnagu (10% – kwalifikujący się):
| Zakwalifikowany | Niezakwalifikowany | |
|---|---|---|
| Przyjęto | 5 | 18 |
| Odrzucono | 5 | 72 |
| Łącznie | 10 | 90 |
|
Odsetek przyjętych uczniów spełniających kryteria: 5/10 = 50% Odsetek odrzuconych uczniów niespełniających kryteriów: 72/90 = 80% Łączny odsetek przyjętych uczniów z Brobdingnagu: (5+18)/100 = 23% |
||
Warunek wyrównanych szans jest spełniony, ponieważ kwalifikujący się studenci z Lilliputu i Brobdingnagu mają 50% szans na przyjęcie, a niekwalifikujący się studenci z Lilliputu i Brobdingnagu mają 80% szans na odrzucenie.
Wyrównane szanse są formalnie zdefiniowane w artykule „Equality of Opportunity in Supervised Learning” w ten sposób: „predyktor Ŷ spełnia warunek wyrównanych szans w odniesieniu do atrybutu chronionego A i wyniku Y, jeśli Ŷ i A są niezależne pod warunkiem Y”.
Estymator
Wycofany interfejs TensorFlow API. Zamiast Estimatorów używaj tf.keras.
oceny,
Używany głównie jako skrót od ocen modeli LLM. Ogólnie rzecz biorąc, oceny to skrót od dowolnej formy oceny.
ocena
Proces pomiaru jakości modelu lub porównywania różnych modeli ze sobą.
Aby ocenić nadzorowany model uczenia maszynowego, zwykle porównujesz go ze zbiorem walidacyjnym i zbiorem testowym. Ocena dużego modelu językowego zwykle obejmuje szersze oceny jakości i bezpieczeństwa.
przykład
Wartości jednego wiersza cech i ewentualnie etykiety. Przykłady w uczeniu nadzorowanym dzielą się na 2 ogólne kategorie:
- Przykład z etykietą składa się z co najmniej 1 cechy i etykiety. Podczas trenowania używane są przykłady z etykietami.
- Nieoznakowany przykład składa się z co najmniej 1 cechy, ale nie ma etykiety. Przykłady bez etykiet są używane podczas wnioskowania.
Załóżmy na przykład, że trenujesz model, który ma określać wpływ warunków pogodowych na wyniki testów uczniów. Oto 3 przykłady z etykietami:
| Funkcje | Etykieta | ||
|---|---|---|---|
| Temperatura | wilgotność, | Ciśnienie | Wynik testu |
| 15 | 47 | 998 | Dobry |
| 19 | 34 | 1020 | Świetna |
| 18 | 92 | 1012 | Niska |
Oto 3 przykłady bez etykiet:
| Temperatura | wilgotność, | Ciśnienie | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
Wiersz zbioru danych jest zwykle surowym źródłem przykładu. Oznacza to, że przykład zwykle składa się z podzbioru kolumn w zbiorze danych. Ponadto cechy w przykładzie mogą też obejmować cechy syntetyczne, takie jak kombinacje cech.
Więcej informacji znajdziesz w sekcji Uczenie nadzorowane w kursie Wprowadzenie do uczenia maszynowego.
experience replay
W uczeniu się przez wzmocnienie technika DQN używana do zmniejszania korelacji czasowych w danych treningowych. Agent przechowuje przejścia stanu w buforze powtórki, a następnie próbkuje przejścia z bufora powtórki, aby utworzyć dane treningowe.
błąd eksperymentatora
Zobacz efekt potwierdzenia.
problem eksplodującego gradientu,
Tendencja gradientów w głębokich sieciach neuronowych (zwłaszcza rekurencyjnych sieciach neuronowych) do stania się zaskakująco stromymi (wysokimi). Strome gradienty często powodują bardzo duże aktualizacje wag każdego węzła w głębokiej sieci neuronowej.
Modele, w których występuje problem z eksplodującym gradientem, stają się trudne lub niemożliwe do wytrenowania. Obcinanie gradientu może rozwiązać ten problem.
Porównaj z problemem znikającego gradientu.
P
F1
Wskaźnik klasyfikacji binarnej, który opiera się na precyzji i czułości. Oto wzór:
zgodność z prawdą,
W świecie uczenia maszynowego jest to właściwość opisująca model, którego dane wyjściowe są oparte na rzeczywistości. Faktyczność to pojęcie, a nie rodzaj danych. Załóżmy na przykład, że wysyłasz do dużego modelu językowego ten prompt:
Jaki jest wzór chemiczny soli kuchennej?
Model optymalizujący pod kątem faktów odpowiedziałby:
NaCl
Można założyć, że wszystkie modele powinny opierać się na faktach. Niektóre prompty, np. te poniżej, powinny jednak skłaniać model generatywnej AI do optymalizacji kreatywności, a nie rzetelności.
Ułóż limeryk o astronautce i gąsienicy.
Jest mało prawdopodobne, że powstały limeryk będzie oparty na rzeczywistości.
Kontrast z uzasadnieniem.
ograniczenie obiektywności
Stosowanie ograniczenia w algorytmie, aby zapewnić spełnienie co najmniej jednej definicji obiektywności. Przykłady ograniczeń związanych z uczciwością:- Przetwarzanie końcowe danych wyjściowych modelu.
- Zmiana funkcji straty w celu uwzględnienia kary za naruszenie rodzaju danych dotyczących sprawiedliwości.
- bezpośrednie dodawanie ograniczenia matematycznego do problemu optymalizacyjnego;
wskaźnik obiektywności,
Matematyczna definicja „obiektywności”, którą można zmierzyć. Do najczęściej używanych wskaźników sprawiedliwości należą:
Wiele wskaźników obiektywności wzajemnie się wyklucza. Więcej informacji znajdziesz w sekcji Brak spójnych wskaźników obiektywności.
wynik fałszywie negatywny (FN),
Przykład, w którym model błędnie przewiduje klasę negatywną. Na przykład model przewiduje, że dana wiadomość e-mail nie jest spamem (klasa negatywna), ale w rzeczywistości jest spamem.
współczynnik wyników fałszywie negatywnych,
Odsetek rzeczywistych przykładów pozytywnych, dla których model błędnie przewidział klasę negatywną. Współczynnik fałszywie negatywnych wyników oblicza się według tego wzoru:
Więcej informacji znajdziesz w sekcji Progi i macierz pomyłek w szybkim szkoleniu z uczenia maszynowego.
wynik fałszywie pozytywny (FP),
Przykład, w którym model błędnie przewiduje klasę pozytywną. Na przykład model przewiduje, że dana wiadomość e-mail to spam (klasa pozytywna), ale w rzeczywistości nie jest to spam.
Więcej informacji znajdziesz w sekcji Progi i macierz pomyłek w szybkim szkoleniu z uczenia maszynowego.
współczynnik wyników fałszywie pozytywnych (FPR),
Odsetek rzeczywistych przykładów negatywnych, dla których model błędnie przewidział klasę pozytywną. Współczynnik fałszywie dodatnich wyników oblicza się według tego wzoru:
Współczynnik wyników fałszywie pozytywnych to oś X na krzywej ROC.
Więcej informacji znajdziesz w sekcji Klasyfikacja: ROC i AUC w szybkim szkoleniu z uczenia maszynowego.
szybki spadek
Technika trenowania, która zwiększa wydajność dużych modeli językowych. Szybkie zmniejszanie polega na szybkim zmniejszaniu szybkości uczenia podczas trenowania. Ta strategia pomaga zapobiegać nadmiernemu dopasowaniu modelu do danych treningowych i zwiększa uogólnianie.
cecha [in context of machine learning]
Zmienna wejściowa modelu uczenia maszynowego. Przykład składa się z co najmniej 1 cechy. Załóżmy na przykład, że trenujesz model, aby określić wpływ warunków pogodowych na wyniki testów uczniów. W tabeli poniżej znajdziesz 3 przykłady, z których każdy zawiera 3 cechy i 1 etykietę:
| Funkcje | Etykieta | ||
|---|---|---|---|
| Temperatura | wilgotność, | Ciśnienie | Wynik testu |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
Kontrast z etykietą.
Więcej informacji znajdziesz w sekcji Uczenie z nadzorem w kursie Wprowadzenie do uczenia maszynowego.
kombinacja cech,
Cechy syntetyczne utworzone przez „skrzyżowanie” cech kategorycznych lub podzielonych na przedziały.
Rozważmy na przykład model „prognozowania nastroju”, który przedstawia temperaturę w jednym z tych 4 przedziałów:
freezingchillytemperatewarm
i przedstawia prędkość wiatru w jednym z tych 3 zakresów:
stilllightwindy
Bez kombinacji cech model liniowy trenuje się niezależnie na podstawie każdego z 7 wcześniejszych różnych przedziałów. Model trenuje więc np.freezing niezależnie od trenowania np.windy.
Możesz też utworzyć kombinację cech temperatury i prędkości wiatru. Ta syntetyczna cecha miałaby 12 możliwych wartości:
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
Dzięki kombinacjom cech model może się nauczyć różnic w nastroju między freezing-windy a freezing-still.
Jeśli utworzysz syntetyczną funkcję z 2 funkcji, z których każda ma wiele różnych przedziałów, wynikowa kombinacja funkcji będzie miała ogromną liczbę możliwych kombinacji. Jeśli na przykład jedna funkcja ma 1000 grup, a druga 2000 grup, to wynikowa kombinacja funkcji ma 2 000 000 grup.
Formalnie krzyżowanie to iloczyn kartezjański.
Kombinacje cech są najczęściej używane w modelach liniowych, a rzadko w sieciach neuronowych.
Więcej informacji znajdziesz w artykule Dane kategorialne: kombinacje cech w Szybkim szkoleniu z uczenia maszynowego.
ekstrakcja wyróżników
Proces obejmujący te kroki:
- określanie, które funkcje mogą być przydatne podczas trenowania modelu;
- przekształcanie nieprzetworzonych danych ze zbioru danych w skuteczne wersje tych funkcji;
Możesz na przykład uznać, że temperature to przydatna funkcja. Następnie możesz poeksperymentować z podziałem na przedziały, aby zoptymalizować to, czego model może się nauczyć z różnych temperature zakresów.
Inżynieria cech jest czasami nazywana ekstrakcją cech lub featurizacją.
Więcej informacji znajdziesz w sekcji Dane liczbowe: jak model przetwarza dane za pomocą wektorów cech w kursie Machine Learning Crash Course.
wyodrębnianie cech,
Przeciążony termin, który ma jedną z tych definicji:
- Pobieranie pośrednich reprezentacji cech obliczonych przez model bez nadzoru lub wstępnie wytrenowany (np. wartości warstwy ukrytej w sieci neuronowej) w celu użycia ich jako danych wejściowych w innym modelu.
- Synonim terminu ekstrakcja wyróżników.
znaczenie cech,
Synonim terminu znaczenie zmiennych.
zestaw funkcji,
Grupa cech, na podstawie których trenowany jest Twój model systemu uczącego się. Na przykład prosty zestaw cech modelu, który prognozuje ceny mieszkań, może składać się z kodu pocztowego, wielkości nieruchomości i jej stanu.
specyfikacja funkcji
Opisuje informacje wymagane do wyodrębnienia danych cech z bufora protokołu tf.Example. Ponieważ bufor protokołu tf.Example jest tylko kontenerem na dane, musisz określić te elementy:
- Dane do wyodrębnienia (czyli klucze funkcji)
- Typ danych (np. float lub int)
- długość (stała lub zmienna);
wektor cech,
Tablica wartości cechy składająca się z przykładu. Wektor cech jest używany jako dane wejściowe podczas trenowania i wnioskowania. Na przykład wektor cech modelu z 2 oddzielnymi cechami może wyglądać tak:
[0.92, 0.56]
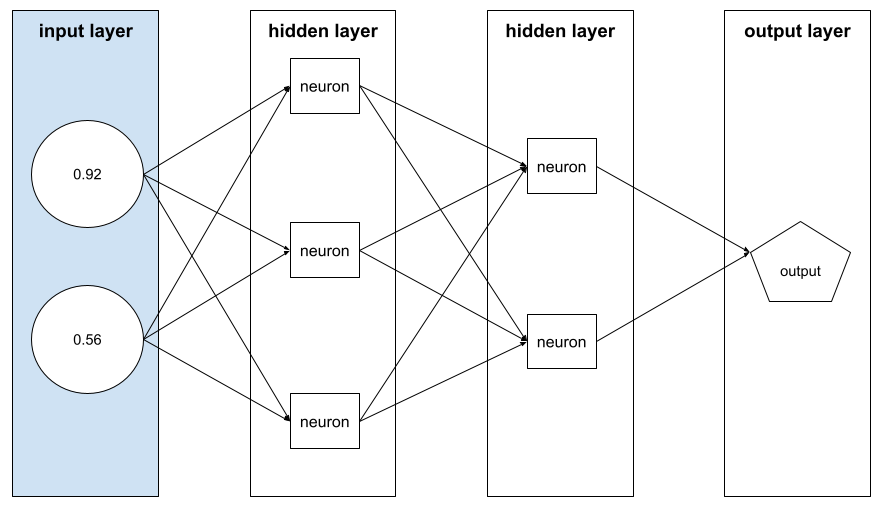
Każdy przykład zawiera inne wartości wektora cech, więc wektor cech dla następnego przykładu może wyglądać tak:
[0.73, 0.49]
Inżynieria cech określa, jak reprezentować cechy w wektorze cech. Na przykład binarna cecha kategorialna z 5 możliwymi wartościami może być reprezentowana za pomocą kodowania 1-z-N. W tym przypadku część wektora cech dla konkretnego przykładu będzie składać się z czterech zer i jednej wartości 1,0 na trzeciej pozycji:
[0.0, 0.0, 1.0, 0.0, 0.0]
Załóżmy na przykład, że model składa się z 3 cech:
- binarna cecha kategorialna z 5 możliwymi wartościami reprezentowanymi za pomocą kodowania 1-z-N, np.
[0.0, 1.0, 0.0, 0.0, 0.0]; - kolejną binarną cechę kategorialną z 3 możliwymi wartościami reprezentowanymi za pomocą kodowania 1 z n, np.
[0.0, 0.0, 1.0]. - cecha zmiennoprzecinkowa, np.
8.3.
W tym przypadku wektor cech każdego przykładu będzie reprezentowany przez 9 wartości. Biorąc pod uwagę przykładowe wartości z poprzedniej listy, wektor cech będzie wyglądać tak:
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
Więcej informacji znajdziesz w sekcji Dane liczbowe: jak model przetwarza dane za pomocą wektorów cech w kursie Machine Learning Crash Course.
featurization
Proces wyodrębniania cech ze źródła wejściowego, takiego jak dokument lub film, i mapowania tych cech na wektor cech.
Niektórzy eksperci w dziedzinie uczenia maszynowego używają terminu „featurization” jako synonimu inżynierii cech lub ekstrakcji cech.
sfederowane uczenie się
Rozproszone podejście do uczenia maszynowego, w którym trenowane są modele uczenia maszynowego za pomocą zdecentralizowanych przykładów znajdujących się na urządzeniach, takich jak smartfony. W sfederowanym uczeniu się podzbiór urządzeń pobiera bieżący model z centralnego serwera koordynującego. Urządzenia wykorzystują przykłady przechowywane na urządzeniach do ulepszania modelu. Urządzenia przesyłają następnie ulepszenia modelu (ale nie przykłady szkoleniowe) na serwer koordynujący, gdzie są one agregowane z innymi aktualizacjami, aby uzyskać ulepszony model globalny. Po agregacji aktualizacje modelu obliczone przez urządzenia nie są już potrzebne i można je odrzucić.
Przykłady treningowe nigdy nie są przesyłane, więc uczenie sfederowane jest zgodne z zasadami ochrony prywatności, które dotyczą ukierunkowanego zbierania danych i minimalizacji danych.
Więcej informacji znajdziesz w komiksie o sfederowanym uczeniu się (tak, to komiks).
pętla informacji zwrotnych
W uczeniu maszynowym sytuacja, w której prognozy modelu wpływają na dane treningowe tego samego lub innego modelu. Na przykład model, który poleca filmy, będzie wpływać na to, jakie filmy zobaczą użytkownicy, co z kolei wpłynie na kolejne modele rekomendacji filmów.
Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: pytania, które warto zadać w kursie Machine Learning Crash Course.
sieć neuronowa z propagacją w przód (FFN),
Sieć neuronowa bez połączeń cyklicznych ani rekurencyjnych. Na przykład tradycyjne głębokie sieci neuronowe to sieci neuronowe typu feedforward. W przeciwieństwie do rekurencyjnych sieci neuronowych, które mają charakter cykliczny.
uczenie z małą liczbą przykładów
Metoda uczenia maszynowego, często stosowana do klasyfikacji obiektów, zaprojektowana do trenowania skutecznych modeli klasyfikacji na podstawie niewielkiej liczby przykładów treningowych.
Zobacz też uczenie „one-shot” i uczenie „zero-shot”.
prompty „few-shot”
Prompt zawierający więcej niż 1 przykład (kilka przykładów) pokazujący, jak powinien odpowiadać duży model językowy. Na przykład ten długi prompt zawiera 2 przykłady pokazujące modelowi językowemu, jak odpowiadać na zapytanie.
| Elementy jednego promptu | Uwagi |
|---|---|
| Jaka jest oficjalna waluta w wybranym kraju? | Pytanie, na które ma odpowiedzieć LLM. |
| Francja: EUR | Przykład. |
| Wielka Brytania: GBP | Inny przykład. |
| Indie: | Faktyczne zapytanie. |
Prompty typu „few-shot” zwykle dają lepsze wyniki niż prompty typu „zero-shot” i prompty typu „one-shot”. Prompty „few-shot” wymagają jednak dłuższego prompta.
Prompty „few-shot” to forma uczenia się „few-shot” stosowana w uczeniu się na podstawie promptów.
Więcej informacji znajdziesz w szybkim szkoleniu z uczenia maszynowego w sekcji Projektowanie promptów.
Skrzypce
Biblioteka konfiguracji oparta na Pythonie, która konfiguruje wartości funkcji i klas bez inwazyjnego kodu ani infrastruktury. W przypadku Pax i innych baz kodu ML te funkcje i klasy reprezentują modele oraz trenowanie hiperparametrów.
Fiddle zakłada, że bazy kodu uczenia maszynowego są zwykle podzielone na:
- Kod biblioteki, który definiuje warstwy i optymalizatory.
- Kod „łączący” zbiór danych, który wywołuje biblioteki i łączy wszystko ze sobą.
Fiddle rejestruje strukturę wywołań kodu łączącego w nieocenionej i zmiennej formie.
dostrajanie,
Drugi etap trenowania modelu wstępnie wytrenowanego, który jest dostosowany do konkretnego zadania i ma na celu dopracowanie parametrów modelu pod kątem konkretnego zastosowania. Na przykład pełna sekwencja trenowania niektórych dużych modeli językowych wygląda tak:
- Wstępne trenowanie: trenowanie dużego modelu językowego na obszernym ogólnym zbiorze danych, np. na wszystkich stronach Wikipedii w języku angielskim.
- Dostrajanie: trenowanie wstępnie wytrenowanego modelu w celu wykonywania konkretnego zadania, np. odpowiadania na pytania medyczne. Dostrajanie zwykle obejmuje setki lub tysiące przykładów związanych z konkretnym zadaniem.
Inny przykład: pełna sekwencja trenowania dużego modelu obrazów wygląda tak:
- Wstępne trenowanie: wytrenuj duży model obrazów na olbrzymim zbiorze ogólnych obrazów, np. na wszystkich obrazach w Wikimedia Commons.
- Dostrojenie: trenowanie wstępnie wytrenowanego modelu w celu wykonania określonego zadania, np. generowania obrazów orek.
Dostrajanie może obejmować dowolną kombinację tych strategii:
- Zmiana wszystkich dotychczasowych parametrów wstępnie wytrenowanego modelu. Czasami nazywa się to pełnym dostrajaniem.
- Zmiana tylko niektórych parametrów wstępnie wytrenowanego modelu (zwykle warstw najbliższych warstwie wyjściowej), przy jednoczesnym zachowaniu innych parametrów (zwykle warstw najbliższych warstwie wejściowej). Zobacz dostrajanie konkretnych parametrów.
- Dodawanie kolejnych warstw, zwykle na istniejących warstwach najbliższych warstwie wyjściowej.
Dostrajanie to forma uczenia transferowego. Dlatego dostrajanie może wykorzystywać inną funkcję straty lub inny typ modelu niż te, które zostały użyte do wytrenowania wstępnie wytrenowanego modelu. Możesz na przykład dostroić wstępnie wytrenowany duży model obrazów, aby uzyskać model regresji, który zwraca liczbę ptaków na obrazie wejściowym.
Porównaj dostrajanie z tymi terminami:
Więcej informacji znajdziesz w sekcji Dostrajanie w szybkim szkoleniu z uczenia maszynowego.
Model lampy błyskowej
Rodzina stosunkowo małych modeli Gemini zoptymalizowanych pod kątem szybkości i niskich opóźnień. Modele Flash są przeznaczone do szerokiego zakresu zastosowań, w których kluczowe są szybkie odpowiedzi i wysoka przepustowość.
Len
Wysokowydajna biblioteka open source do uczenia głębokiego oparta na JAX. Flax udostępnia funkcje do trenowania sieci neuronowych, a także metody oceny ich wydajności.
Flaxformer
Biblioteka open source Transformer oparta na Flax, przeznaczona głównie do przetwarzania języka naturalnego i badań multimodalnych.
zapomnij o bramie
Część komórki pamięci długiej i krótkotrwałej, która reguluje przepływ informacji przez komórkę. Bramki zapominania zachowują kontekst, decydując, które informacje odrzucić ze stanu komórki.
model podstawowy
Bardzo duży wytrenowany model, który został wytrenowany na ogromnym i zróżnicowanym zbiorze treningowym. Model podstawowy może wykonywać obie te czynności:
- dobrze reagować na szeroki zakres żądań,
- Służyć jako model podstawowy do dodatkowego dostrajania lub innego dostosowywania.
Innymi słowy, model podstawowy ma już duże możliwości w ogólnym sensie, ale można go dodatkowo dostosować, aby był jeszcze bardziej przydatny w konkretnym zadaniu.
odsetek sukcesów
Wskaźnik oceny wygenerowanego tekstu modelu ML. Ułamek sukcesów to liczba „udanych” wygenerowanych wyników tekstowych podzielona przez łączną liczbę wygenerowanych wyników tekstowych. Jeśli na przykład duży model językowy wygenerował 10 bloków kodu, z których 5 zostało wykonanych prawidłowo, odsetek sukcesów wyniesie 50%.
Chociaż odsetek sukcesów jest ogólnie przydatny w statystyce, w uczeniu maszynowym ten wskaźnik jest przydatny głównie do pomiaru zadań weryfikowalnych, takich jak generowanie kodu lub rozwiązywanie problemów matematycznych.
pełna funkcja softmax,
Synonim słowa softmax.
Porównaj z próbkowaniem kandydatów.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: klasyfikacja wieloklasowa w kursie Machine Learning Crash Course.
w pełni połączona warstwa,
Warstwa ukryta, w której każdy węzeł jest połączony z każdym węzłem w kolejnej warstwie ukrytej.
Warstwa w pełni połączona jest też nazywana warstwą gęstą.
przekształcenie funkcji,
Funkcja, która przyjmuje funkcję jako dane wejściowe i zwraca przekształconą funkcję jako dane wyjściowe. JAX używa przekształceń funkcji.
G
GAN
Skrót od generatywnej sieci przeciwniczej.
Gemini
Ekosystem obejmujący najbardziej zaawansowaną AI od Google. Elementy tego ekosystemu to:
- Różne modele Gemini.
- Interaktywny interfejs konwersacyjny do modelu Gemini. Użytkownicy wpisują prompty, a Gemini na nie odpowiada.
- Różne interfejsy Gemini API.
- Różne usługi biznesowe oparte na modelach Gemini, np. Gemini w Google Cloud.
Modele Gemini
najnowocześniejsze modele multimodalne oparte na Transformerze od Google. Modele Gemini zostały zaprojektowane specjalnie z myślą o integracji z agentami.
Użytkownicy mogą wchodzić w interakcje z modelami Gemini na różne sposoby, m.in. za pomocą interaktywnego interfejsu dialogowego i zestawów SDK.
Gemma
Rodzina lekkich modeli otwartych, które powstały na podstawie tych samych badań i technologii, które zostały wykorzystane do stworzenia modeli Gemini. Dostępnych jest kilka różnych modeli Gemma, z których każdy oferuje inne funkcje, takie jak widzenie, kodowanie i wykonywanie instrukcji. Więcej informacji znajdziesz w sekcji Gemma.
Generatywna AI lub genAI
Skrót od generatywnej AI.
uogólnienie
Zdolność modelu do tworzenia prawidłowych prognoz na podstawie nowych, wcześniej niewidzianych danych. Model, który potrafi uogólniać, jest przeciwieństwem modelu, który jest przetrenowany.
Więcej informacji znajdziesz w sekcji Uogólnianie w szybkim szkoleniu z uczenia maszynowego.
krzywa generalizacji,
Wykres straty trenowania i straty walidacji w funkcji liczby iteracji.
Krzywa uogólnienia może pomóc w wykryciu możliwego przetrenowania. Na przykład poniższa krzywa uogólnienia sugeruje przetrenowanie, ponieważ ostatecznie strata w przypadku zbioru weryfikacyjnego staje się znacznie większa niż strata w przypadku zbioru treningowego.
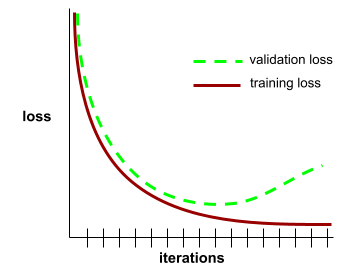
Więcej informacji znajdziesz w sekcji Uogólnianie w szybkim szkoleniu z uczenia maszynowego.
uogólniony model liniowy,
Uogólnienie modeli regresji metodą najmniejszych kwadratów, które są oparte na szumie Gaussa, na inne typy modeli opartych na innych rodzajach szumu, takich jak szum Poissona lub szum kategorialny. Przykłady uogólnionych modeli liniowych:
- regresja logistyczna,
- regresja wieloklasowa,
- regresja metodą najmniejszych kwadratów,
Parametry uogólnionego modelu liniowego można znaleźć za pomocą optymalizacji wypukłej.
Uogólnione modele liniowe mają te właściwości:
- Średnia prognoza optymalnego modelu regresji metodą najmniejszych kwadratów jest równa średniej etykiecie w danych treningowych.
- Średnie prawdopodobieństwo prognozowane przez optymalny model regresji logistycznej jest równe średniej etykiecie w danych treningowych.
Możliwości uogólnionego modelu liniowego są ograniczone przez jego cechy. W przeciwieństwie do modelu głębokiego uogólniony model liniowy nie może „uczyć się nowych cech”.
wygenerowany tekst,
Ogólnie rzecz biorąc, tekst wygenerowany przez model ML. Podczas oceny dużych modeli językowych niektóre wskaźniki porównują wygenerowany tekst z tekstem referencyjnym. Załóżmy na przykład, że chcesz sprawdzić, jak skutecznie model ML tłumaczy z francuskiego na holenderski. W tym przypadku:
- Wygenerowany tekst to tłumaczenie na język niderlandzki, które wygenerował model ML.
- Tekst referencyjny to tłumaczenie na język niderlandzki utworzone przez tłumacza (lub oprogramowanie).
Pamiętaj, że niektóre strategie oceny nie obejmują tekstu referencyjnego.
generatywna sieć współzawodnicząca (GAN),
System do tworzenia nowych danych, w którym generator tworzy dane, a dyskryminator określa, czy utworzone dane są prawidłowe.
Więcej informacji znajdziesz w kursie o generatywnych sieciach przeciwstawnych.
generatywna AI,
To nowa, przełomowa dziedzina, która nie ma formalnej definicji. Większość ekspertów zgadza się jednak, że modele generatywnej AI mogą tworzyć („generować”) treści, które są:
- złożone,
- spójny,
- oryginał
Przykłady generatywnej AI:
- Duże modele językowe, które mogą generować zaawansowane oryginalne teksty i odpowiadać na pytania.
- Model generowania obrazów, który może tworzyć unikalne obrazy.
- modele generowania dźwięku i muzyki, które mogą komponować oryginalną muzykę lub generować realistyczną mowę;
- modele do generowania filmów, które mogą tworzyć oryginalne filmy;
Niektóre starsze technologie, w tym LSTM i RNN, również mogą generować oryginalne i spójne treści. Niektórzy eksperci uważają te wcześniejsze technologie za generatywną AI, podczas gdy inni uważają, że prawdziwa generatywna AI wymaga bardziej złożonych wyników niż te wcześniejsze technologie.
Porównaj z prognozującym uczeniem maszynowym.
model generatywny
W praktyce model, który:
- Tworzy (generuje) nowe przykłady na podstawie zbioru danych treningowych. Na przykład model generatywny może tworzyć poezję po wytrenowaniu na zbiorze wierszy. Do tej kategorii należy generator w ramach generatywnej sieci przeciwstawnej.
- Określa prawdopodobieństwo, że nowy przykład pochodzi ze zbioru treningowego lub został utworzony za pomocą tego samego mechanizmu, który utworzył zbiór treningowy. Na przykład po wytrenowaniu na zbiorze danych składającym się z zdań w języku angielskim model generatywny może określić prawdopodobieństwo, że nowe dane wejściowe są prawidłowym zdaniem w języku angielskim.
Model generatywny może teoretycznie rozpoznać rozkład przykładów lub określonych cech w zbiorze danych. Czyli:
p(examples)
Modele uczenia nienadzorowanego mają charakter generatywny.
Porównaj z modelami dyskryminacyjnymi.
generator
Podsystem w generatywnej sieci przeciwstawnej, który tworzy nowe przykłady.
Porównaj z modelem dyskryminacyjnym.
zanieczyszczenie Giniego,
Dane podobne do entropii. Rozdzielacze używają wartości pochodzących z nieczystości Giniego lub entropii do tworzenia warunków klasyfikacji drzew decyzyjnych. Przyrost informacji jest obliczany na podstawie entropii. Nie ma powszechnie akceptowanego odpowiednika terminu dla danych pochodnych z nieczystości Giniego, ale te nienazwane dane są równie ważne jak przyrost informacji.
Zanieczyszczenie Giniego jest też nazywane wskaźnikiem Giniego lub po prostu gini.
złoty zbiór danych,
Zestaw ręcznie wyselekcjonowanych danych, które odzwierciedlają dane podstawowe. Zespoły mogą używać co najmniej 1 złotego zbioru danych do oceny jakości modelu.
Niektóre zbiory danych referencyjnych obejmują różne poddomeny prawdy podstawowej. Na przykład złoty zbiór danych do klasyfikacji obrazów może uwzględniać warunki oświetlenia i rozdzielczość obrazu.
złota odpowiedź
Odpowiedź, która jest uznawana za dobrą. Na przykład w przypadku tego prompta:
2 + 2
Idealna odpowiedź to:
4
Google AI Studio
Narzędzie Google z przyjaznym interfejsem, które umożliwia eksperymentowanie z dużymi modelami językowymi Google i tworzenie przy ich użyciu aplikacji. Szczegółowe informacje znajdziesz na stronie głównej Google AI Studio.
GPT (Generative Pre-trained Transformer)
Rodzina dużych modeli językowych opartych na architekturze Transformer opracowanych przez OpenAI.
Warianty GPT mogą być stosowane w przypadku wielu modalności, w tym:
- generowanie obrazów (np. ImageGPT),
- generowanie obrazów z tekstu (np. DALL-E);
gradient
Wektor pochodnych cząstkowych względem wszystkich zmiennych niezależnych. W uczeniu maszynowym gradient to wektor pochodnych cząstkowych funkcji modelu. Gradient wskazuje kierunek największego wzrostu.
gromadzenie gradientów,
Technika propagacji wstecznej, która aktualizuje parametry tylko raz na epokę, a nie raz na iterację. Po przetworzeniu każdej mini-partii akumulacja gradientów po prostu aktualizuje bieżącą sumę gradientów. Następnie po przetworzeniu ostatniej mini-partii w epoce system aktualizuje parametry na podstawie sumy wszystkich zmian gradientu.
Akumulacja gradientu jest przydatna, gdy rozmiar wsadu jest bardzo duży w porównaniu z ilością pamięci dostępnej na potrzeby trenowania. Gdy problemem jest pamięć, naturalną tendencją jest zmniejszenie rozmiaru partii. Zmniejszenie rozmiaru partii w przypadku normalnej propagacji wstecznej zwiększa liczbę aktualizacji parametrów. Akumulacja gradientu pozwala uniknąć problemów z pamięcią, a jednocześnie skutecznie trenować model.
wzmocnione gradientowo drzewa decyzyjne (GBT),
Rodzaj lasu decyzyjnego, w którym:
- Trenowanie opiera się na wzmocnieniu gradientowym.
- Słabym modelem jest drzewo decyzyjne.
Więcej informacji znajdziesz w lekcji o drzewach decyzyjnych z wzmocnieniem gradientowym w kursie Decision Forests.
wzmocnienie gradientowe,
Algorytm trenowania, w którym słabe modele są trenowane w celu iteracyjnego poprawiania jakości (zmniejszania straty) silnego modelu. Przykładem słabego modelu może być model liniowy lub mały model drzewa decyzyjnego. Silny model staje się sumą wszystkich wcześniej wytrenowanych słabych modeli.
W najprostszej formie wzmacniania gradientowego w każdej iteracji trenowany jest słaby model, który ma przewidywać gradient funkcji straty silnego modelu. Następnie dane wyjściowe modelu o wysokiej skuteczności są aktualizowane przez odjęcie przewidywanego gradientu, podobnie jak w przypadku metody gradientu prostego.
gdzie:
- $F_{0}$ to model początkowy.
- $F_{i+1}$ to kolejny silny model.
- $F_{i}$ to bieżący model o wysokiej skuteczności.
- $\xi$ to wartość z zakresu od 0,0 do 1,0, zwana kurczeniem, która jest analogiczna do szybkości uczenia w metodzie spadku gradientowego.
- $f_{i}$ to słaby model wytrenowany do przewidywania gradientu funkcji straty $F_{i}$.
Nowoczesne odmiany wzmacniania gradientowego uwzględniają też w obliczeniach drugą pochodną (hesjan) funkcji straty.
Drzewa decyzyjne są często używane jako słabe modele w metodzie gradient boosting. Zobacz drzewa decyzyjne z wzmocnieniem gradientowym.
ograniczanie gradientu,
Powszechnie stosowany mechanizm ograniczania problemu eksplodującego gradientu przez sztuczne ograniczanie (obcinanie) maksymalnej wartości gradientów podczas korzystania z metody gradientu prostego do trenowania modelu.
metoda spadku wzdłuż gradientu,
Technika matematyczna służąca do minimalizowania straty. Metoda gradientu prostego iteracyjnie dostosowuje wagi i odchylenia, stopniowo znajdując najlepszą kombinację, która minimalizuje straty.
Metoda gradientu prostego jest starsza od uczenia maszynowego – i to znacznie.
Więcej informacji znajdziesz w sekcji Regresja liniowa: metoda gradientowa w kursie Machine Learning Crash Course.
wykres
W TensorFlow jest to specyfikacja obliczeń. Węzły na wykresie reprezentują operacje. Krawędzie są skierowane i reprezentują przekazywanie wyniku operacji (Tensor) jako operandu do innej operacji. Użyj TensorBoard, aby zwizualizować wykres.
wykonanie grafu
Środowisko programistyczne TensorFlow, w którym program najpierw tworzy graf, a następnie wykonuje cały graf lub jego część. W TensorFlow 1.x domyślnym trybem wykonywania jest wykonywanie wykresu.
Kontrastuje z wykonywaniem natychmiastowym.
zachłanna strategia
W uczeniu ze wzmocnieniem strategia, która zawsze wybiera działanie o najwyższym oczekiwanym zwrocie.
uzasadnienie
Właściwość modelu, którego dane wyjściowe są oparte na konkretnych materiałach źródłowych. Załóżmy na przykład, że jako dane wejściowe („kontekst”) do dużego modelu językowego podajesz cały podręcznik fizyki. Następnie zadajesz dużemu modelowi językowemu pytanie z zakresu fizyki. Jeśli odpowiedź modelu odzwierciedla informacje zawarte w tym podręczniku, to model jest oparty na tym podręczniku.Pamiętaj, że model oparty na danych nie zawsze jest modelem rzetelnym. Na przykład podręcznik fizyki może zawierać błędy.
dane podstawowe
Rzeczywistość.
co faktycznie się wydarzyło.
Rozważmy na przykład model klasyfikacji binarnej, który przewiduje, czy student pierwszego roku ukończy studia w ciągu 6 lat. Dane podstawowe dla tego modelu to informacja, czy uczeń ukończył studia w ciągu 6 lat.
błąd uogólnienia,
Zakładanie, że to, co dotyczy jednej osoby, dotyczy też wszystkich członków danej grupy. Skutki błędu atrybucji grupowej mogą się nasilić, jeśli do zbierania danych zostanie użyte próbkowanie wygodne. W przypadku próby niereprezentatywnej atrybucje mogą nie odzwierciedlać rzeczywistości.
Zobacz też błąd jednorodności grupy obcej i stronniczość wewnątrzgrupową. Więcej informacji znajdziesz też w artykule Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
H
halucynacje
Generowanie przez model generatywnej AI, który ma na celu przedstawienie twierdzenia dotyczącego rzeczywistego świata, wyników, które wydają się wiarygodne, ale są niezgodne z faktami. Na przykład model generatywnej AI, który twierdzi, że Barack Obama zmarł w 1865 roku, halucynuje.
wyliczanie skrótu
W uczeniu maszynowym mechanizm dzielenia na przedziały danych kategorycznych, zwłaszcza gdy liczba kategorii jest duża, ale liczba kategorii faktycznie występujących w zbiorze danych jest stosunkowo mała.
Na przykład na Ziemi występuje około 73 tys. gatunków drzew. Możesz przedstawić każdy z 73 tys. gatunków drzew w 73 tys. oddzielnych kategoriach. Jeśli jednak w zbiorze danych występuje tylko 200 gatunków drzew, możesz użyć funkcji skrótu, aby podzielić je na około 500 grup.
Jeden kosz może zawierać wiele gatunków drzew. Na przykład haszowanie może umieścić w tym samym koszyku baobab i klon czerwony, czyli 2 gatunki o różnym materiale genetycznym. Niezależnie od tego haszowanie jest nadal dobrym sposobem mapowania dużych zbiorów kategorii na wybraną liczbę koszyków. Mieszanie przekształca cechę kategorialną o dużej liczbie możliwych wartości w znacznie mniejszą liczbę wartości przez grupowanie wartości w deterministyczny sposób.
Więcej informacji znajdziesz w sekcji Dane kategorialne: słownictwo i kodowanie 1-z-N w kursie Machine Learning Crash Course.
heurystyczny,
Proste i szybkie rozwiązanie problemu. Na przykład: „Dzięki heurystyce udało nam się osiągnąć dokładność na poziomie 86%. Gdy przeszliśmy na głęboką sieć neuronową, dokładność wzrosła do 98%."
warstwa ukryta
Warstwa w sieci neuronowej między warstwą wejściową (cechy) a warstwą wyjściową (prognoza). Każda warstwa ukryta składa się z co najmniej 1 neuronu. Na przykład ta sieć neuronowa zawiera 2 warstwy ukryte: pierwszą z 3 neuronami i drugą z 2 neuronami:
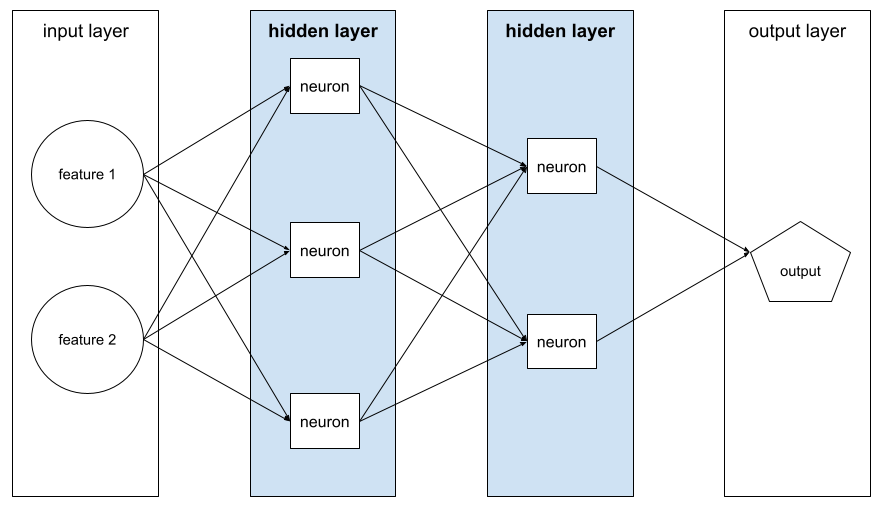
Głęboka sieć neuronowa zawiera więcej niż jedną warstwę ukrytą. Na przykład ilustracja powyżej przedstawia głęboką sieć neuronową, ponieważ model zawiera 2 warstwy ukryte.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: węzły i warstwy ukryte w kursie Machine Learning Crash Course.
grupowanie hierarchiczne,
Kategoria algorytmów klastrowania, które tworzą drzewo klastrów. Klastrowanie hierarchiczne sprawdza się w przypadku danych hierarchicznych, takich jak taksonomia botaniczna. Istnieją 2 rodzaje algorytmów klastrowania hierarchicznego:
- Metoda aglomeracyjna najpierw przypisuje każdy przykład do własnego klastra, a następnie iteracyjnie łączy najbliższe klastry, aby utworzyć drzewo hierarchiczne.
- Dzielące grupowanie najpierw grupuje wszystkie przykłady w 1 klaster, a następnie iteracyjnie dzieli go na drzewo hierarchiczne.
Kontrast z klastrowaniem opartym na centroidach.
Więcej informacji znajdziesz w sekcji Algorytmy klastrowania w kursie Klastrowanie.
wspinaczka po wzgórzach,
Algorytm iteracyjnego ulepszania („wspinania się pod górę”) modelu uczenia maszynowego, dopóki model nie przestanie się poprawiać („nie osiągnie szczytu góry”). Ogólna postać algorytmu jest następująca:
- Utwórz model początkowy.
- Twórz nowe modele kandydujące, wprowadzając niewielkie zmiany w sposobie trenowania lub dostrajania. Może to wymagać pracy z nieco innym zbiorem treningowym lub innymi hiperparametrami.
- Oceń nowe modele kandydatów i wykonaj jedną z tych czynności:
- Jeśli model kandydujący osiąga lepsze wyniki niż model początkowy, staje się nowym modelem początkowym. W takim przypadku powtórz kroki 1, 2 i 3.
- Jeśli żaden model nie jest lepszy od modelu początkowego, oznacza to, że osiągnięto szczyt i należy przerwać iterację.
Wskazówki dotyczące dostrajania hiperparametrów znajdziesz w przewodniku po dostrajaniu uczenia głębokiego. Więcej informacji o inżynierii cech znajdziesz w modułach danych w szybkim szkoleniu z uczenia maszynowego.
funkcja straty zawiasu,
Rodzina funkcji strat do klasyfikacji, która ma na celu znalezienie granicy decyzyjnej jak najdalej od każdego przykładu treningowego, co maksymalizuje margines między przykładami a granicą. KSVM używają funkcji straty zawiasowej (lub powiązanej funkcji, np. kwadratowej funkcji straty zawiasowej). W przypadku klasyfikacji binarnej funkcja straty zawiasowej jest zdefiniowana w ten sposób:
gdzie y to prawdziwa etykieta, czyli -1 lub +1, a y' to surowe dane wyjściowe modelu klasyfikacji:
W związku z tym wykres funkcji straty zawiasowej w zależności od (y * y') wygląda tak:

obciążenie historyczne,
Rodzaj obciążenia, które już istnieje w świecie i zostało uwzględnione w zbiorze danych. Te uprzedzenia odzwierciedlają istniejące stereotypy kulturowe, nierówności demograficzne i uprzedzenia wobec określonych grup społecznych.
Rozważmy na przykład model klasyfikacji, który przewiduje, czy wnioskodawca nie spłaci pożyczki. Model ten został wytrenowany na podstawie danych historycznych dotyczących niespłaconych pożyczek z lat 80. XX wieku, pochodzących z lokalnych banków w 2 różnych społecznościach. Jeśli w przeszłości wnioskodawcy ze społeczności A byli 6 razy bardziej narażeni na niewywiązanie się ze spłaty pożyczki niż wnioskodawcy ze społeczności B, model może nauczyć się historycznego obciążenia, co spowoduje, że będzie mniej skłonny do zatwierdzania pożyczek w społeczności A, nawet jeśli historyczne warunki, które spowodowały wyższe wskaźniki niewywiązania się ze spłaty w tej społeczności, nie będą już miały znaczenia.
Więcej informacji znajdziesz w module Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
dane wstrzymane,
Przykłady celowo nieużywane („wyłączone”) podczas trenowania. Zbiór danych do weryfikacji i zbiór danych testowych to przykłady danych wyłączonych. Dane wstrzymane pomagają ocenić zdolność modelu do uogólniania na dane inne niż te, na których został wytrenowany. Utrata w zbiorze wstrzymanym zapewnia lepsze oszacowanie utraty w niewidzianym zbiorze danych niż utrata w zbiorze treningowym.
host
Podczas trenowania modelu uczenia maszynowego na chipach akceleratora (GPU lub TPU) część systemu, która kontroluje oba te elementy:
- ogólny przepływ kodu;
- wyodrębnianie i przekształcanie potoku wejściowego,
Host działa zwykle na procesorze, a nie na układzie akceleratora. Urządzenie przetwarza tensory na układach akceleratora.
ocena przez człowieka,
Proces, w którym osoby oceniają jakość danych wyjściowych modelu ML, np. dwujęzyczni użytkownicy oceniają jakość tłumaczenia maszynowego. Weryfikacja manualna jest szczególnie przydatna w przypadku modeli, które nie mają jednej prawidłowej odpowiedzi.
Porównaj z oceną automatyczną i oceną przez automatyczny program oceny.
proces z udziałem człowieka
Luźno zdefiniowany idiom, który może oznaczać jedno z tych stwierdzeń:
- Zasady krytycznego lub sceptycznego podejścia do danych wyjściowych generatywnej AI.
- Strategia lub system zapewniający, że użytkownicy pomagają kształtować, oceniać i ulepszać zachowanie modelu. Utrzymanie człowieka w procesie umożliwia AI korzystanie zarówno z inteligencji maszynowej, jak i ludzkiej. Na przykład system, w którym AI generuje kod, a inżynierowie oprogramowania go sprawdzają, jest systemem z udziałem człowieka.
hiperparametr
Zmienne, które Ty lub usługa dostrajania hiperparametrówdostosowuje podczas kolejnych uruchomień trenowania modelu. Na przykład szybkość uczenia jest hiperparametrem. Przed jedną sesją trenowania możesz ustawić współczynnik uczenia na 0,01. Jeśli uznasz, że 0,01 to zbyt wysoka wartość, możesz ustawić współczynnik uczenia na 0,003 w przypadku następnej sesji trenowania.
Z kolei parametry to różne wagi i odchylenia, których model uczy się podczas trenowania.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
hiperpłaszczyzna
Granica, która dzieli przestrzeń na dwie podprzestrzenie. Na przykład linia to hiperpłaszczyzna w 2 wymiarach, a płaszczyzna to hiperpłaszczyzna w 3 wymiarach. W uczeniu maszynowym hiperpłaszczyzna jest zwykle granicą oddzielającą przestrzeń wielowymiarową. Metoda SVM z funkcją jądra wykorzystuje hiperpłaszczyzny do oddzielania klas pozytywnych od klas negatywnych, często w przestrzeni o bardzo dużej liczbie wymiarów.
I
i.i.d.
Skrót od niezależnych i identycznie rozłożonych.
rozpoznawanie obrazów
Proces klasyfikowania obiektów, wzorów lub pojęć na obrazie. Rozpoznawanie obrazów jest też znane jako klasyfikacja obrazów.
Więcej informacji znajdziesz w artykule ML Practicum: Image Classification (w języku angielskim).
Więcej informacji znajdziesz w kursie ML Practicum: Image Classification.
niezrównoważony zbiór danych
Synonim terminu zbiór danych z niezrównoważonymi klasami.
nieświadome uprzedzenia
Automatyczne tworzenie powiązań lub założeń na podstawie modeli mentalnych i wspomnień. Uprzedzenia ukryte mogą wpływać na:
- Jak dane są zbierane i klasyfikowane.
- Jak projektowane i opracowywane są systemy uczące się.
Na przykład podczas tworzenia modelu klasyfikacji do rozpoznawania zdjęć ślubnych inżynier może użyć obecności białej sukni na zdjęciu jako cechy. Białe suknie były jednak zwyczajowe tylko w określonych epokach i w określonych kulturach.
Zobacz też błąd potwierdzenia.
imputacja
Skrócona forma przypisywania wartości.
brak spójnych wskaźników obiektywności,
Koncepcja, że niektóre pojęcia obiektywności są wzajemnie niekompatybilne i nie można ich spełnić jednocześnie. Dlatego nie ma jednego uniwersalnego wskaźnika, który można by zastosować do wszystkich problemów związanych z uczeniem maszynowym.
Może to zniechęcać, ale brak spójnych wskaźników obiektywności nie oznacza, że działania na rzecz obiektywności są bezcelowe. Zamiast tego sugeruje, że obiektywność musi być definiowana w kontekście danego problemu ML, aby zapobiegać szkodom związanym z jego przypadkami użycia.
Więcej informacji o braku spójnych wskaźników obiektywności znajdziesz w artykule „(Nie)możliwość obiektywności”.
uczenie w kontekście,
Synonim promptów „few-shot”.
niezależne i identycznie rozłożone (i.i.d.)
Dane pochodzące z rozkładu, który się nie zmienia, a każda wylosowana wartość nie zależy od wartości wylosowanych wcześniej. Rozkład i.i.d. jest gazem idealnym uczenia maszynowego – przydatną konstrukcją matematyczną, która jednak niemal nigdy nie występuje w rzeczywistości. Na przykład rozkład odwiedzających stronę internetową może być niezależny i identyczny w krótkim przedziale czasu, tzn. rozkład nie zmienia się w tym krótkim przedziale czasu, a wizyta jednej osoby jest na ogół niezależna od wizyty innej osoby. Jeśli jednak rozszerzysz ten przedział czasu, mogą się pojawić różnice sezonowe w liczbie odwiedzających stronę.
Zobacz też niestacjonarność.
sprawiedliwość indywidualna,
Miara sprawiedliwości, która sprawdza, czy podobne osoby są klasyfikowane w podobny sposób. Na przykład Akademia Brobdingnagian może chcieć spełnić kryterium sprawiedliwości indywidualnej, zapewniając, że dwóch uczniów z identycznymi ocenami i wynikami testów standaryzowanych ma takie samo prawdopodobieństwo przyjęcia.
Pamiętaj, że sprawiedliwość indywidualna zależy całkowicie od tego, jak zdefiniujesz „podobieństwo” (w tym przypadku oceny i wyniki testów). Jeśli wskaźnik podobieństwa nie uwzględnia ważnych informacji (np. poziomu trudności programu nauczania), możesz wprowadzić nowe problemy związane ze sprawiedliwością.
Więcej informacji o sprawiedliwości indywidualnej znajdziesz w artykule „Fairness Through Awareness”.
wnioskowanie
W tradycyjnym uczeniu maszynowym proces prognozowania polegający na zastosowaniu wytrenowanego modelu do nieoznaczonych przykładów. Więcej informacji znajdziesz w module Uczenie z nadzorem w kursie Wprowadzenie do uczenia maszynowego.
W dużych modelach językowych wnioskowanie to proces polegający na używaniu wytrenowanego modelu do generowania odpowiedzi na prompt.
W statystyce wnioskowanie ma nieco inne znaczenie. Szczegółowe informacje znajdziesz w artykule w Wikipedii na temat wnioskowania statystycznego.
ścieżka wnioskowania
W drzewie decyzyjnym podczas wnioskowania przykład przechodzi od korzenia do innych warunków, kończąc na liściu. Na przykład na poniższym schemacie decyzyjnym grubsze strzałki pokazują ścieżkę wnioskowania dla przykładu o tych wartościach cech:
- x = 7
- y = 12
- z = -3
Ścieżka wnioskowania na poniższej ilustracji przechodzi przez 3 warunki, zanim dotrze do węzła końcowego (Zeta).

Trzy grube strzałki pokazują ścieżkę wnioskowania.
Więcej informacji znajdziesz w sekcji Drzewa decyzyjne w kursie Lasy decyzyjne.
przyrost informacji
W lasach decyzyjnych różnica między entropią węzła a ważoną (według liczby przykładów) sumą entropii jego węzłów podrzędnych. Entropia węzła to entropia przykładów w tym węźle.
Rozważmy na przykład te wartości entropii:
- entropia węzła nadrzędnego = 0,6
- entropia jednego węzła podrzędnego z 16 odpowiednimi przykładami = 0,2.
- entropia innego węzła podrzędnego z 24 odpowiednimi przykładami = 0,1
40% przykładów znajduje się w jednym węźle podrzędnym, a 60% – w drugim. Dlatego:
- ważona suma entropii węzłów podrzędnych = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Zatem przyrost informacji wynosi:
- przyrost informacji = entropia węzła nadrzędnego – ważona suma entropii węzłów podrzędnych
- przyrost informacji = 0,6 – 0,14 = 0,46
Większość rozdzielaczy dąży do tworzenia warunków, które maksymalizują przyrost informacji.
stronniczość wewnątrzgrupowa,
Faworyzowanie własnej grupy lub własnych cech. Jeśli testerami lub oceniającymi są znajomi, rodzina lub współpracownicy dewelopera uczenia maszynowego, może to spowodować błąd związany z przynależnością do grupy, który unieważni testowanie produktu lub zbiór danych.
Stronniczość wewnątrzgrupowa jest formą błędu uogólnienia. Zobacz też błąd jednorodności grupy obcej.
Więcej informacji znajdziesz w sekcji Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
generator danych wejściowych,
Mechanizm, za pomocą którego dane są ładowane do sieci neuronowej.
Generator danych wejściowych można traktować jako komponent odpowiedzialny za przetwarzanie surowych danych na tensory, które są iterowane w celu generowania partii na potrzeby trenowania, oceny i wnioskowania.
warstwa wejściowa
Warstwa sieci neuronowej, która zawiera wektor cech. Oznacza to, że warstwa wejściowa dostarcza przykłady do trenowania lub wnioskowania. Na przykład warstwa wejściowa w tym przykładzie sieci neuronowej składa się z 2 cech:
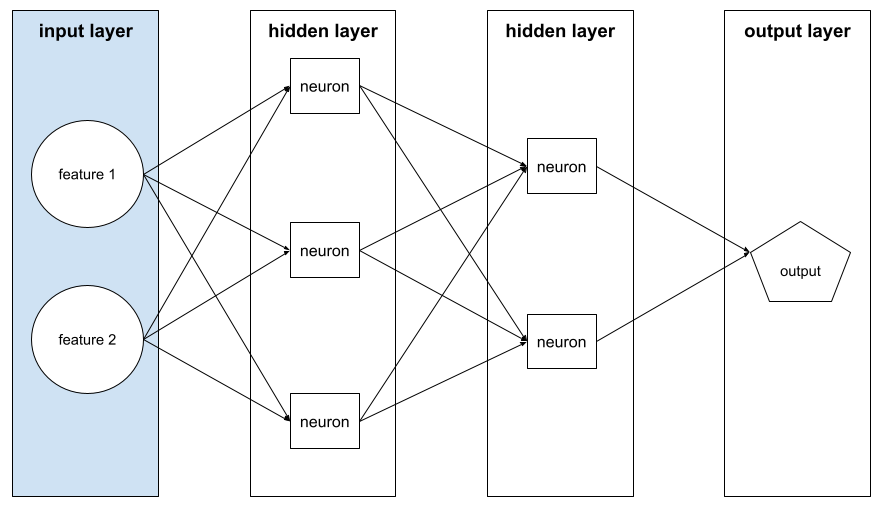
warunek w zbiorze
W drzewie decyzyjnym warunek, który sprawdza, czy w zbiorze elementów znajduje się jeden element. Na przykład ten warunek należy do zbioru:
house-style in [tudor, colonial, cape]
Podczas wnioskowania, jeśli wartość stylu domu feature wynosi tudor, colonial lub cape, warunek ten jest spełniony. Jeśli wartość funkcji stylu domu jest inna (np. ranch), warunek przyjmuje wartość „Nie”.
Warunki zbioru zwykle prowadzą do bardziej wydajnych drzew decyzyjnych niż warunki, które testują cechy zakodowane metodą 1-z-N.
instancja
Synonim słowa przykład.
dostrajanie przy użyciu instrukcji,
Rodzaj dostrajania, który zwiększa zdolność modelu generatywnej AI do wykonywania instrukcji. Dostrajanie przy użyciu instrukcji polega na trenowaniu modelu na podstawie serii promptów z instrukcjami, które zwykle obejmują szeroki zakres zadań. Model dostrojony do instrukcji zwykle generuje przydatne odpowiedzi na pytania bez przykładów w przypadku różnych zadań.
Porównaj z:
interpretowalność,
Możliwość wyjaśnienia lub przedstawienia rozumowania modelu uczenia maszynowego w sposób zrozumiały dla człowieka.
Na przykład większość modeli regresji liniowej jest bardzo łatwa do interpretacji. (Wystarczy spojrzeć na wytrenowane wagi dla każdej cechy). Las decyzji jest też bardzo łatwy do interpretacji. Interpretowalność niektórych modeli wymaga jednak rozbudowanej wizualizacji.
Do interpretowania modeli ML możesz używać narzędzia do analizowania interpretowalności (LIT).
zgodność ocen
Miara częstotliwości, z jaką weryfikatorzy zgadzają się ze sobą podczas wykonywania zadania. Jeśli oceniający nie zgadzają się ze sobą, może być konieczne ulepszenie instrukcji zadania. Czasami nazywana też zgodnością między oceniającymi lub wiarygodnością między oceniającymi. Zobacz też współczynnik kappa Cohena, który jest jednym z najpopularniejszych wskaźników zgodności ocen.
Więcej informacji znajdziesz w sekcji Dane kategorialne: typowe problemy w kursie Machine Learning Crash Course.
współczynnik podobieństwa (IoU)
Przecięcie dwóch zbiorów podzielone przez ich sumę. W uczeniu maszynowym w przypadku zadań wykrywania obrazów współczynnik podobieństwa służy do pomiaru dokładności prognozowanej ramki ograniczającej modelu w odniesieniu do ramki ograniczającej opartej na bezpośredniej obserwacji. W tym przypadku współczynnik podobieństwa dla tych 2 ramek to stosunek obszaru nakładania się do obszaru całkowitego, a jego wartość mieści się w zakresie od 0 (brak nakładania się prognozowanej ramki ograniczającej i ramki ograniczającej danych podstawowych) do 1 (prognozowana ramka ograniczająca i ramka ograniczająca danych podstawowych mają dokładnie te same współrzędne).
Na przykład na obrazie poniżej:
- Prognozowana ramka ograniczająca (współrzędne wyznaczające miejsce, w którym model przewiduje, że znajduje się stolik nocny na obrazie) jest zaznaczona na fioletowo.
- Rzeczywiste pole ograniczające (współrzędne wyznaczające miejsce, w którym w obrazie znajduje się stolik nocny) jest zaznaczone na zielono.
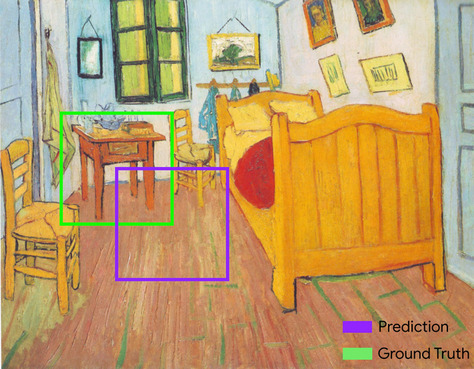
W tym przypadku część wspólna ramek ograniczających dla prognozy i danych podstawowych (po lewej poniżej) wynosi 1, a suma ramek ograniczających dla prognozy i danych podstawowych (po prawej poniżej) wynosi 7, więc współczynnik podobieństwa to \(\frac{1}{7}\).
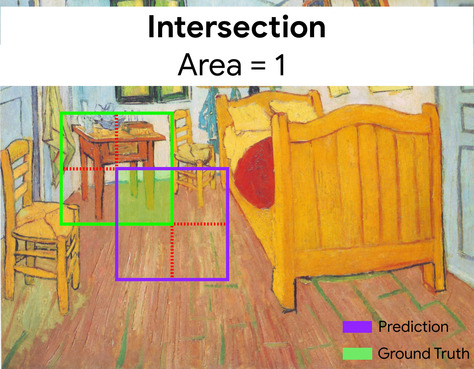
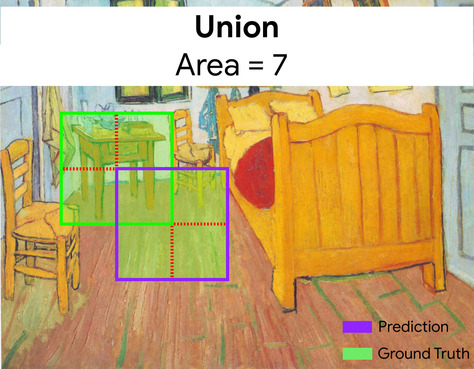
IoU
Skrót od intersection over union (współczynnik podobieństwa).
macierz produktów
W systemach rekomendacji macierz wektorów osadzania generowana przez faktoryzację macierzy, która zawiera ukryte sygnały dotyczące każdego produktu. Każdy wiersz macierzy produktów zawiera wartość pojedynczej cechy ukrytej dla wszystkich produktów. Rozważmy na przykład system rekomendacji filmów. Każda kolumna w macierzy elementów reprezentuje jeden film. Sygnały ukryte mogą reprezentować gatunki lub być trudniejszymi do zinterpretowania sygnałami, które obejmują złożone interakcje między gatunkiem, gwiazdami, wiekiem filmu lub innymi czynnikami.
Macierz elementów ma tyle samo kolumn co macierz docelowa, która jest faktoryzowana. Na przykład w systemie rekomendacji filmów, który ocenia 10 tys. tytułów, macierz elementów będzie miała 10 tys. kolumn.
items
W systemie rekomendacji są to obiekty, które system rekomenduje. Na przykład filmy to produkty, które poleca wypożyczalnia filmów, a książki to produkty, które poleca księgarnia.
iteracja
Pojedyncza aktualizacja parametrów modelu, czyli wag i odchyleń modelu, podczas trenowania. Rozmiar wsadu określa, ile przykładów model przetwarza w jednej iteracji. Jeśli na przykład rozmiar partii wynosi 20, model przetwarza 20 przykładów przed dostosowaniem parametrów.
Podczas trenowania sieci neuronowej pojedyncza iteracja obejmuje 2 przejścia:
- Przejście w przód w celu oceny utraty w przypadku pojedynczej partii.
- Przejście wsteczne (propagacja wsteczna) w celu dostosowania parametrów modelu na podstawie wartości funkcji straty i tempa uczenia się.
Więcej informacji znajdziesz w sekcji Spadek gradientu w szybkim szkoleniu z uczenia maszynowego.
J
JAX
Biblioteka obliczeń tablicowych, która łączy XLA (Accelerated Linear Algebra) i automatyczne różniczkowanie na potrzeby obliczeń numerycznych o wysokiej wydajności. JAX udostępnia prosty i wydajny interfejs API do pisania przyspieszonego kodu numerycznego z możliwością łączenia transformacji. JAX oferuje takie funkcje jak:
grad(automatyczne różnicowanie)jit(kompilacja w odpowiednim czasie)vmap(automatyczna wektoryzacja lub przetwarzanie wsadowe)pmap(równoległość)
JAX to język do wyrażania i komponowania przekształceń kodu numerycznego, analogiczny do biblioteki NumPy w Pythonie, ale o znacznie szerszym zakresie. (Biblioteka .numpy w JAX jest w zasadzie odpowiednikiem biblioteki NumPy w Pythonie, ale została całkowicie przepisana).
JAX szczególnie dobrze sprawdza się w przyspieszaniu wielu zadań uczenia maszynowego dzięki przekształcaniu modeli i danych w formę odpowiednią do równoległego przetwarzania na procesorach graficznych i TPU akceleratorach.
Flax, Optax, Pax i wiele innych bibliotek są oparte na infrastrukturze JAX.
K
Keras
Popularny interfejs Python API do uczenia maszynowego. Keras działa w kilku platformach do głębokiego uczenia, w tym w TensorFlow, gdzie jest dostępny jako tf.keras.
Maszyny wektorów nośnych z jądrem (KSVM)
Algorytm klasyfikacji, który dąży do zmaksymalizowania marginesu między klasami pozytywnymi i negatywnymi przez mapowanie wektorów danych wejściowych na przestrzeń o większej liczbie wymiarów. Rozważmy na przykład problem klasyfikacji, w którym wejściowy zbiór danych ma 100 cech. Aby zmaksymalizować margines między klasami pozytywnymi i negatywnymi, model KSVM może wewnętrznie mapować te cechy na przestrzeń o milionie wymiarów. KSVM używa funkcji straty o nazwie strata zawiasowa.
punkty kluczowe
współrzędne konkretnych elementów na obrazie. Na przykład w przypadku modelu rozpoznawania obrazów, który rozróżnia gatunki kwiatów, punktami kluczowymi mogą być środek każdego płatka, łodyga, pręcik itp.
weryfikacja krzyżowa k-krotna,
Algorytm prognozujący zdolność modelu do uogólniania na nowe dane. Liczba k w k-krotnej walidacji krzyżowej odnosi się do liczby równych grup, na które dzielisz przykłady w zbiorze danych. Oznacza to, że trenujesz i testujesz model k razy. W każdej rundzie trenowania i testowania inna grupa jest zbiorem testowym, a wszystkie pozostałe grupy stają się zbiorem treningowym. Po k rundach trenowania i testowania obliczasz średnią i odchylenie standardowe wybranych danych testowych.
Załóżmy na przykład, że zbiór danych zawiera 120 przykładów. Załóżmy, że ustawiasz k = 4. Dlatego po przetasowaniu przykładów dzielisz zbiór danych na 4 równe grupy po 30 przykładów i przeprowadzasz 4 rundy trenowania i testowania:
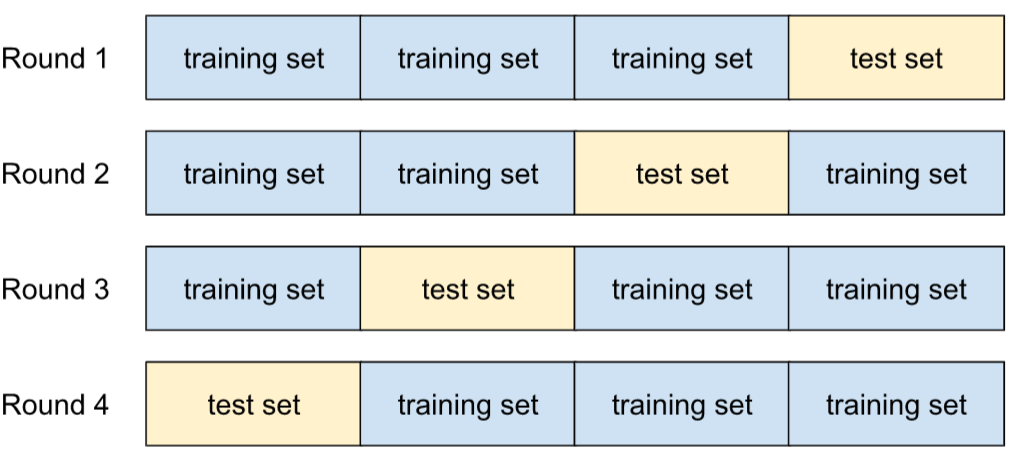
Na przykład błąd średniokwadratowy (MSE) może być najbardziej miarodajnym wskaźnikiem w przypadku modelu regresji liniowej. Dlatego obliczysz średnią i odchylenie standardowe MSE we wszystkich 4 rundach.
k-średnich
Popularny algorytm klasteryzacji, który grupuje przykłady w uczeniu nienadzorowanym. Algorytm k-średnich wykonuje te czynności:
- Iteracyjnie określa najlepsze k punktów środkowych (zwanych centroidami).
- Przypisuje każdy przykład do najbliższego centroidu. Przykłady znajdujące się najbliżej tego samego środka należą do tej samej grupy.
Algorytm k-średnich wybiera lokalizacje centroidów, aby zminimalizować skumulowany kwadrat odległości od każdego przykładu do najbliższego centroidu.
Rozważmy na przykład ten wykres zależności wysokości psa od jego szerokości:

Jeśli k=3, algorytm k-średnich wyznaczy 3 środki. Każdy przykład jest przypisywany do najbliższego centroidu, co daje 3 grupy:

Załóżmy, że producent chce określić idealne rozmiary małych, średnich i dużych swetrów dla psów. Trzy centroidy określają średnią wysokość i średnią szerokość każdego psa w danym klastrze. Dlatego producent powinien prawdopodobnie określać rozmiary swetrów na podstawie tych 3 środków. Pamiętaj, że centroid klastra zwykle nie jest przykładem w tym klastrze.
Powyższe ilustracje przedstawiają algorytm k-średnich na przykładach z tylko 2 cechami (wysokością i szerokością). Pamiętaj, że algorytm k-średnich może grupować przykłady na podstawie wielu cech.
Więcej informacji znajdziesz w sekcji Co to jest klastrowanie metodą k-średnich? w kursie Klastrowanie.
k-mediana
Algorytm grupowania blisko powiązany z algorytmem k-średnich. Praktyczna różnica między tymi 2 rodzajami jest następująca:
- W algorytmie k-średnich centroidy są wyznaczane przez zminimalizowanie sumy kwadratów odległości między kandydatem na centroid a każdym z jego przykładów.
- W przypadku algorytmu k-medoidów centroidy są wyznaczane przez minimalizowanie sumy odległości między kandydatem na centroid a każdym z jego przykładów.
Zwróć uwagę, że definicje odległości są też inne:
- Algorytm k-średnich opiera się na odległości euklidesowej od środka klastra do przykładu. (W przypadku 2 wymiarów odległość euklidesowa oznacza użycie twierdzenia Pitagorasa do obliczenia przeciwprostokątnej). Na przykład odległość k-średnich między punktami (2,2) a (5,-2) wynosi:
- Algorytm k-medoids opiera się na odległości Manhattan od środka do przykładu. Ta odległość to suma bezwzględnych różnic w każdym wymiarze. Na przykład odległość k-median między punktami (2,2) i (5,-2) wynosi:
L
Regularyzacja L0
Rodzaj regularyzacji, która nakłada karę na łączną liczbę niezerowych wag w modelu. Na przykład model z 11 wagami o wartości różnej od zera zostanie bardziej obciążony karą niż podobny model z 10 wagami o wartości różnej od zera.
Regularyzacja L0 jest czasami nazywana regularyzacją normy L0.
Utrata sygnału L1
Funkcja straty, która oblicza wartość bezwzględną różnicy między rzeczywistymi wartościami etykiet a wartościami przewidywanymi przez model. Na przykład poniżej przedstawiamy obliczenia utraty L1 dla partii 5 przykładów:
| Rzeczywista wartość przykładu | Wartość prognozowana przez model | Wartość bezwzględna różnicy |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = utrata L1 | ||
Funkcja straty L1 jest mniej wrażliwa na wartości odstające niż funkcja straty L2.
Średni błąd bezwzględny to średnia strata L1 na przykład.
Więcej informacji znajdziesz w sekcji Regresja liniowa: funkcja straty w kursie Machine Learning Crash Course.
regularyzacja L1,
Rodzaj regularyzacji, która powoduje nakładanie kar na wagi proporcjonalnie do sumy wartości bezwzględnych wag. Regularyzacja L1 pomaga sprowadzić wagi nieistotnych lub mało istotnych cech do dokładnie 0. Cechę o wadze 0 można uznać za usuniętą z modelu.
Kontrast z regularyzacją L2.
Funkcja straty L2
Funkcja straty, która oblicza kwadrat różnicy między rzeczywistymi wartościami etykiet a wartościami przewidywanymi przez model. Oto przykład obliczania straty L2 dla partii pięciu przykładów:
| Rzeczywista wartość przykładu | Wartość prognozowana przez model | Kwadrat delty |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 przegrana | ||
Ze względu na podnoszenie do kwadratu funkcja straty L2 wzmacnia wpływ wartości odstających. Oznacza to, że funkcja straty L2 reaguje silniej na nieprawidłowe prognozy niż funkcja straty L1. Na przykład funkcja straty L1 dla poprzedniej partii wyniesie 8, a nie 16. Zwróć uwagę, że 1 wartość odstająca odpowiada 9 z 16 wartości.
Modele regresji zwykle używają funkcji utraty L2.
Błąd średniokwadratowy to średnia strata L2 na przykład. Strata kwadratowa to inna nazwa straty L2.
Więcej informacji znajdziesz w sekcji Regresja logistyczna: funkcja straty i regularyzacja w kursie Machine Learning Crash Course.
regularyzacja L2,
Rodzaj regularyzacji, która powoduje nakładanie kar na wagi proporcjonalnie do sumy kwadratów wag. Regularyzacja L2 pomaga zbliżyć wagi wartości odstających (o wysokich wartościach dodatnich lub niskich wartościach ujemnych) do 0, ale nie do 0. Cechy o wartościach bardzo bliskich 0 pozostają w modelu, ale nie mają dużego wpływu na jego prognozę.
Regularyzacja L2 zawsze poprawia generalizację w modelach liniowych.
Kontrast z regularyzacją L1.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: regularyzacja L2 w szybkim szkoleniu z uczenia maszynowego.
etykieta
W uczeniu maszynowym nadzorowanym „odpowiedź” lub „wynik” w przykładzie.
Każdy przykład z etykietą składa się z co najmniej 1 cechy i etykiety. Na przykład w zbiorze danych do wykrywania spamu etykieta będzie prawdopodobnie miała wartość „spam” lub „nie spam”. W zbiorze danych o opadach deszczu etykietą może być ilość deszczu, która spadła w określonym czasie.
Więcej informacji znajdziesz w sekcji Uczenie nadzorowane w artykule Wprowadzenie do uczenia maszynowego.
przykład oznaczony etykietą,
Przykład zawierający co najmniej 1 cechę i etykietę. Na przykład w tabeli poniżej znajdują się 3 przykłady z etykietami z modelu wyceny domu. Każdy z nich ma 3 cechy i 1 etykietę:
| Liczba sypialni | Liczba łazienek | Wiek domu | Cena domu (etykieta) |
|---|---|---|---|
| 3 | 2 | 15 | 345 tys. zł |
| 2 | 1 | 72 | 179 000 USD |
| 4 | 2 | 34 | 392 000 USD |
W nadzorowanym uczeniu maszynowym modele są trenowane na oznaczonych przykładach i dokonują prognoz na podstawie nieoznaczonych przykładów.
Porównaj przykłady z etykietami z przykładami bez etykiet.
Więcej informacji znajdziesz w sekcji Uczenie nadzorowane w artykule Wprowadzenie do uczenia maszynowego.
wyciek etykiet,
Wada projektu modelu, w której cecha jest zmienną zastępczą etykiety. Rozważmy na przykład model klasyfikacji binarnej, który przewiduje, czy potencjalny klient kupi dany produkt.
Załóżmy, że jedną z cech modelu jest wartość logiczna o nazwie
SpokeToCustomerAgent. Załóżmy ponadto, że pracownik obsługi klienta jest przypisywany dopiero po zakupie produktu przez potencjalnego klienta. Podczas trenowania model szybko nauczy się powiązania między SpokeToCustomerAgent a etykietą.
Więcej informacji znajdziesz w sekcji Monitorowanie potoków w szybkim szkoleniu z uczenia maszynowego.
lambda
Synonim terminu współczynnik regulacji.
Lambda to termin wieloznaczny. Skupiamy się tu na definicji tego terminu w kontekście regularyzacji.
LaMDA (Language Model for Dialogue Applications)
Duży model językowy oparty na architekturze Transformer opracowany przez Google i wytrenowany na dużym zbiorze danych dialogowych, który może generować realistyczne odpowiedzi.
LaMDA: nasza przełomowa technologia konwersacyjna zawiera omówienie.
punkty orientacyjne,
Synonim słowa keypoints.
model językowy
Model, który szacuje prawdopodobieństwo wystąpienia tokena lub sekwencji tokenów w dłuższej sekwencji tokenów.
Więcej informacji znajdziesz w artykule Co to jest model językowy? w Szybkim szkoleniu z uczenia maszynowego.
duży model językowy
Co najmniej model językowy z bardzo dużą liczbą parametrów. Bardziej nieformalnie: dowolny model językowy oparty na architekturze Transformer, np. Gemini lub GPT.
Więcej informacji znajdziesz w sekcji Duże modele językowe (LLM) w szybkim szkoleniu z uczenia maszynowego.
opóźnienie
Czas potrzebny modelowi na przetworzenie danych wejściowych i wygenerowanie odpowiedzi. Odpowiedź o dużym czasie oczekiwania jest generowana dłużej niż odpowiedź o małym czasie oczekiwania.
Na opóźnienie dużych modeli językowych wpływają m.in. te czynniki:
- Długości danych wejściowych i wyjściowych [token]
- Złożoność modelu
- Infrastruktura, na której działa model
Optymalizacja pod kątem opóźnień jest kluczowa w przypadku tworzenia aplikacji, które szybko reagują na działania użytkowników i są dla nich przyjazne.
przestrzeń ukryta,
Synonim przestrzeni wektorów dystrybucyjnych.
warstwa
Zbiór neuronów w sieci neuronowej. Oto 3 najpopularniejsze rodzaje warstw:
- Warstwa wejściowa, która zawiera wartości wszystkich cech.
- Co najmniej 1 ukryta warstwa, która wykrywa nieliniowe zależności między cechami a etykietą.
- Warstwa wyjściowa, która zawiera prognozę.
Na przykład poniższa ilustracja przedstawia sieć neuronową z 1 warstwą wejściową, 2 warstwami ukrytymi i 1 warstwą wyjściową:
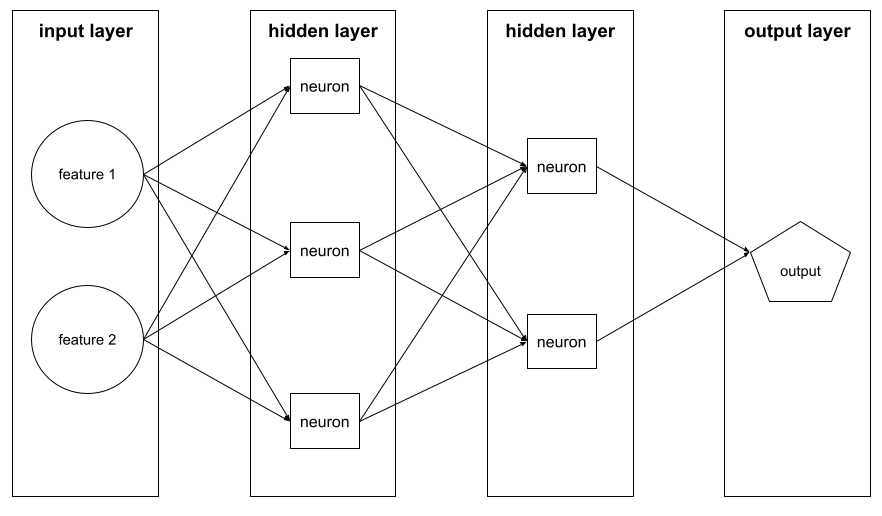
W TensorFlow warstwy to również funkcje Pythona, które przyjmują jako dane wejściowe tensory i opcje konfiguracji, a jako dane wyjściowe generują inne tensory.
Layers API (tf.layers)
Interfejs TensorFlow API do tworzenia głębokiej sieci neuronowej jako kompozycji warstw. Interfejs Layers API umożliwia tworzenie różnych typów warstw, takich jak:
tf.layers.Densedla w pełni połączonej warstwy.tf.layers.Conv2Ddla warstwy konwolucyjnej.
Interfejs Layers API jest zgodny z konwencjami interfejsu Keras Layers API. Oznacza to, że oprócz innego prefiksu wszystkie funkcje w interfejsie Layers API mają takie same nazwy i sygnatury jak ich odpowiedniki w interfejsie Keras Layers API.
liść
Dowolny punkt końcowy w drzewie decyzyjnym. W przeciwieństwie do warunku węzeł końcowy nie przeprowadza testu. Liść jest raczej możliwą prognozą. Liść jest też węzłem końcowym ścieżki wnioskowania.
Na przykład to drzewo decyzyjne zawiera 3 liście:
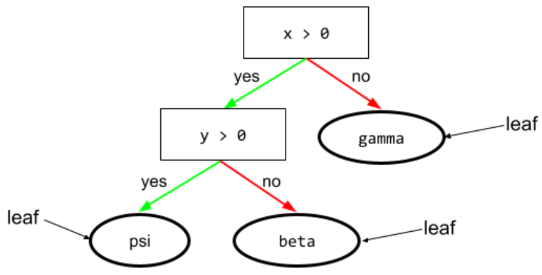
Więcej informacji znajdziesz w sekcji Drzewa decyzyjne w kursie Lasy decyzyjne.
Narzędzie do analizowania interpretowalności (LIT)
Wizualne, interaktywne narzędzie do analizowania modeli i wizualizacji danych.
Możesz użyć narzędzia open source LIT, aby interpretować modele lub wizualizować tekst, obrazy i dane w formie tabel.
tempo uczenia się
Liczba zmiennoprzecinkowa, która informuje algorytm spadku gradientu, jak silnie dostosowywać wagi i odchylenia w każdej iteracji. Na przykład współczynnik uczenia 0,3 dostosowuje wagi i odchylenia 3 razy silniej niż współczynnik uczenia 0,1.
Tempo uczenia się to kluczowy hiperparametr. Jeśli ustawisz zbyt niską szybkość uczenia się, trenowanie potrwa zbyt długo. Jeśli ustawisz zbyt wysokie tempo uczenia się, metoda gradientu prostego często ma problemy z osiągnięciem konwergencji.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
regresja metodą najmniejszych kwadratów,
Model regresji liniowej trenowany przez minimalizowanie straty L2.
Odległość Levenshteina
Miara odległości edycji, która oblicza najmniejszą liczbę operacji usuwania, wstawiania i zamiany wymaganych do zmiany jednego słowa na inne. Na przykład odległość Levenshteina między słowami „heart” i „darts” wynosi 3, ponieważ do przekształcenia jednego słowa w drugie potrzeba co najmniej 3 zmian:
- heart → deart (zamień „h” na „d”)
- deart → dart (usuń „e”)
- dart → darts (dodaj „s”)
Pamiętaj, że powyższa sekwencja nie jest jedyną ścieżką 3 edycji.
jednostajne
Zależność między co najmniej 2 zmiennymi, którą można przedstawić wyłącznie za pomocą dodawania i mnożenia.
Wykres zależności liniowej to linia.
Kontrast z nieliniowymi.
model liniowy,
Model, który przypisuje jedną wagę do każdej cechy, aby tworzyć prognozy. (Modele liniowe również uwzględniają tendencyjność). Z kolei w modelach głębokich relacja między cechami a prognozami jest zwykle nieliniowa.
Modele liniowe są zwykle łatwiejsze do wytrenowania i bardziej zrozumiałe niż modele głębokie. Modele głębokie mogą jednak nauczyć się złożonych relacji między cechami.
Regresja liniowa i regresja logistyczna to 2 rodzaje modeli liniowych.
regresja liniowa,
Rodzaj modelu uczenia maszynowego, w którym spełnione są oba te warunki:
- Model jest modelem liniowym.
- Prognoza to liczba zmiennoprzecinkowa. (Jest to część regresji regresji liniowej).
Porównaj regresję liniową z regresją logistyczną. Porównaj też regresję z klasyfikacją.
Więcej informacji znajdziesz w sekcji Regresja liniowa w szybkim szkoleniu z uczenia maszynowego.
LIT
Skrót od Narzędzia do analizowania interpretowalności (LIT), które było wcześniej znane jako narzędzie do analizowania interpretowalności języka.
LLM
Skrót od dużego modelu językowego.
Oceny LLM
Zestaw danych i punktów odniesienia do oceny wydajności dużych modeli językowych (LLM). Ogólnie rzecz biorąc, oceny LLM:
- pomagać badaczom w określaniu obszarów, w których modele LLM wymagają ulepszeń;
- Przydają się do porównywania różnych LLM i określania, który z nich najlepiej nadaje się do konkretnego zadania.
- pomagać w zapewnieniu bezpieczeństwa i etycznego charakteru modeli LLM;
Więcej informacji znajdziesz w szybkim szkoleniu z uczenia maszynowego w sekcji Duże modele językowe (LLM).
regresja logistyczna
Rodzaj modelu regresji, który prognozuje prawdopodobieństwo. Modele regresji logistycznej mają te cechy:
- Etykieta jest kategoryczna. Termin regresja logistyczna zwykle odnosi się do binarnej regresji logistycznej, czyli modelu, który oblicza prawdopodobieństwa etykiet o 2 możliwych wartościach. Mniej popularny wariant, wielomianowa regresja logistyczna, oblicza prawdopodobieństwa etykiet z więcej niż 2 możliwymi wartościami.
- Funkcja straty podczas trenowania to Log Loss. (W przypadku etykiet z więcej niż 2 możliwymi wartościami można umieścić równolegle kilka jednostek Log Loss).
- Model ma architekturę liniową, a nie głęboką sieć neuronową. Pozostała część tej definicji dotyczy jednak również modeli głębokich, które prognozują prawdopodobieństwa etykiet kategorialnych.
Rozważmy na przykład model regresji logistycznej, który oblicza prawdopodobieństwo, że e-mail wejściowy jest spamem lub nie jest spamem. Załóżmy, że podczas wnioskowania model prognozuje wartość 0,72. Dlatego model szacuje:
- 72% – prawdopodobieństwo, że e-mail jest spamem.
- 28% – prawdopodobieństwo, że e-mail nie jest spamem.
Model regresji logistycznej wykorzystuje tę dwuetapową architekturę:
- Model generuje prognozę pierwotną (y') przez zastosowanie funkcji liniowej cech wejściowych.
- Model używa tej surowej prognozy jako danych wejściowych funkcji sigmoidalnej, która przekształca surową prognozę w wartość z przedziału (0, 1).
Podobnie jak każdy model regresji, model regresji logistycznej prognozuje liczbę. Zwykle jednak liczba ta staje się częścią modelu klasyfikacji binarnej w ten sposób:
- Jeśli przewidywana liczba jest większa niż próg klasyfikacji, model klasyfikacji binarnej prognozuje klasę pozytywną.
- Jeśli przewidywana liczba jest mniejsza niż próg klasyfikacji, model klasyfikacji binarnej przewiduje klasę negatywną.
Więcej informacji znajdziesz w sekcji Regresja logistyczna w szybkim szkoleniu z uczenia maszynowego.
logity,
Wektor surowych (nieznormalizowanych) prognoz generowanych przez model klasyfikacji, który jest zwykle przekazywany do funkcji normalizacji. Jeśli model rozwiązuje problem klasyfikacji wieloklasowej, logity zwykle stają się danymi wejściowymi funkcji softmax. Funkcja softmax generuje następnie wektor (znormalizowanych) prawdopodobieństw z jedną wartością dla każdej możliwej klasy.
Logarytmiczna funkcja straty
Funkcja straty używana w przypadku binarnej regresji logistycznej.
Więcej informacji znajdziesz w sekcji Regresja logistyczna: funkcja straty i regularyzacja w kursie Machine Learning Crash Course.
log-odds
Logarytm szans wystąpienia danego zdarzenia.
Długa pamięć krótkotrwała (LSTM)
Rodzaj komórki w rekurencyjnej sieci neuronowej używanej do przetwarzania sekwencji danych w aplikacjach takich jak rozpoznawanie pisma odręcznego, tłumaczenie maszynowe i generowanie podpisów do obrazów. Sieci LSTM rozwiązują problem z zanikającym gradientem, który występuje podczas trenowania sieci RNN z użyciem długich sekwencji danych. Utrzymują historię w wewnętrznym stanie pamięci na podstawie nowych danych wejściowych i kontekstu z poprzednich komórek w sieci RNN.
LoRA
Skrót od Low-Rank Adaptability (adaptacja niskiego rzędu).
przegrana
Podczas trenowania modelu nadzorowanego mierzy się, jak bardzo prognoza modelu odbiega od jego etykiety.
Funkcja straty oblicza stratę.
Więcej informacji znajdziesz w sekcji Regresja liniowa: funkcja straty w kursie Machine Learning Crash Course.
agregator strat
Rodzaj algorytmu uczenia maszynowego, który zwiększa skuteczność modelu przez połączenie prognoz wielu modeli i wykorzystanie tych prognoz do utworzenia jednej prognozy. W rezultacie agregator funkcji straty może zmniejszyć wariancję prognoz i zwiększyć ich dokładność.
krzywa strat,
Wykres straty jako funkcji liczby iteracji trenowania. Poniższy wykres przedstawia typową krzywą utraty:
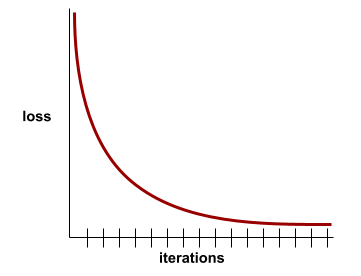
Krzywe funkcji straty mogą pomóc Ci określić, kiedy model zbiega się lub nadmiernie dopasowuje się.
Krzywe strat mogą przedstawiać wszystkie te rodzaje strat:
Zobacz też krzywą generalizacji.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: interpretowanie krzywych funkcji straty w kursie Machine Learning Crash Course.
funkcja straty,
Podczas trenowania lub testowania funkcja matematyczna, która oblicza stratę na partii przykładów. Funkcja straty zwraca mniejszą stratę w przypadku modeli, które generują dobre prognozy, niż w przypadku modeli, które generują złe prognozy.
Celem trenowania jest zwykle minimalizowanie straty zwracanej przez funkcję straty.
Istnieje wiele różnych rodzajów funkcji straty. Wybierz odpowiednią funkcję straty dla rodzaju tworzonego modelu. Na przykład:
- Funkcja straty L2 (lub średnia kwadratowa błędów) to funkcja straty dla regresji liniowej.
- Log Loss to funkcja straty dla regresji logistycznej.
powierzchnia funkcji straty,
Wykres wagi w porównaniu z utratą wagi. Metoda gradientu prostego ma na celu znalezienie wagi(wag), dla których powierzchnia funkcji straty osiąga lokalne minimum.
Adaptacja niskiego rzędu (LoRA)
Wydajna pod względem liczby parametrów technika dostrajania, która „zamraża” wstępnie wytrenowane wagi modelu (tak, aby nie można było ich już modyfikować), a następnie wstawia do modelu niewielki zestaw wag, które można trenować. Ten zestaw wag, które można wytrenować (zwany też „macierzami aktualizacji”), jest znacznie mniejszy niż model podstawowy, a dzięki temu jego trenowanie jest znacznie szybsze.
LoRA zapewnia te korzyści:
- Poprawia jakość prognoz modelu w domenie, w której zastosowano dostrajanie.
- Dostosowuje się szybciej niż techniki, które wymagają dostosowania wszystkich parametrów modelu.
- Zmniejsza koszt obliczeniowy wnioskowania, umożliwiając jednoczesne udostępnianie wielu wyspecjalizowanych modeli, które korzystają z tego samego modelu bazowego.
LSTM
Skrót od Long Short-Term Memory.
M
systemy uczące się
To programy lub systemy, które trenują model na podstawie danych wejściowych. Wytrenowany model może tworzyć przydatne prognozy na podstawie nowych (wcześniej niewykorzystanych) danych pobranych z tego samego rozkładu co dane użyte do trenowania modelu.
Uczenie maszynowe to także dziedzina nauki zajmująca się tymi programami lub systemami.
Więcej informacji znajdziesz w kursie Wprowadzenie do uczenia maszynowego.
tłumaczenie maszynowe,
Używanie oprogramowania (zwykle modelu systemu uczącego się) do przekształcania tekstu z jednego języka na inny, np. z angielskiego na japoński.
klasa większościowa,
Etykieta, która występuje częściej w zbiorze danych z niezrównoważonymi klasami. Na przykład w zbiorze danych zawierającym 99% etykiet negatywnych i 1% etykiet pozytywnych etykiety negatywne stanowią klasę większościową.
Kontrast z klasą mniejszościową.
Więcej informacji znajdziesz w sekcji Zbiory danych: niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
Proces decyzyjny Markowa (MDP)
Graf reprezentujący model podejmowania decyzji, w którym decyzje (lub działania) są podejmowane w celu poruszania się po sekwencji stanów przy założeniu, że obowiązuje własność Markowa. W uczeniu ze wzmocnieniem te przejścia między stanami zwracają liczbową nagrodę.
Własność Markowa
Właściwość niektórych środowisk, w których przejścia między stanami są całkowicie determinowane przez informacje zawarte w bieżącym stanie i działaniu agenta.
zamaskowany model językowy,
Model językowy, który przewiduje prawdopodobieństwo wystąpienia tokenów kandydatów w miejscach oznaczonych jako puste w sekwencji. Na przykład zamaskowany model językowy może obliczyć prawdopodobieństwa dla proponowanych słów, które mają zastąpić podkreślenie w tym zdaniu:
____ w kapeluszu wrócił.
W literaturze zamiast podkreślenia zwykle używa się ciągu znaków „MASK”. Na przykład:
„MASK” na kapeluszu wrócił.
Większość nowoczesnych zamaskowanych modeli językowych jest dwukierunkowa.
matplotlib
Biblioteka open source Pythona do tworzenia wykresów 2D. matplotlib pomaga wizualizować różne aspekty uczenia maszynowego.
rozkład macierzy,
W matematyce mechanizm znajdowania macierzy, których iloczyn skalarny jest przybliżeniem macierzy docelowej.
W systemach rekomendacji macierz docelowa często zawiera oceny produktów przez użytkowników. Na przykład macierz docelowa systemu rekomendacji filmów może wyglądać tak, jak poniżej. Liczby całkowite dodatnie to oceny użytkowników, a 0 oznacza, że użytkownik nie ocenił filmu:
| Casablanca | Filadelfijska opowieść | Czarna Pantera | Wonder Woman | Pulp Fiction | |
|---|---|---|---|---|---|
| Użytkownik 1 | 5,0 | 3,0 | 0,0 | 2,0 | 0,0 |
| Użytkownik 2 | 4.0 | 0,0 | 0,0 | 1,0 | 5,0 |
| Użytkownik 3 | 3,0 | 1,0 | 4.0 | 5,0 | 0,0 |
System rekomendacji filmów ma na celu przewidywanie ocen użytkowników dla filmów, które nie zostały jeszcze ocenione. Na przykład czy użytkownik 1 polubi film Czarna Pantera?
Jednym z podejść do systemów rekomendacji jest użycie faktoryzacji macierzy do wygenerowania tych 2 macierzy:
- Macierz użytkowników o wymiarach liczba użytkowników × liczba wymiarów osadzania.
- Macierz elementów o wymiarach liczba wymiarów osadzania × liczba elementów.
Na przykład zastosowanie faktoryzacji macierzy w przypadku 3 użytkowników i 5 produktów może dać te macierze użytkowników i produktów:
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
Iloczyn skalarny macierzy użytkowników i macierzy elementów daje macierz rekomendacji, która zawiera nie tylko pierwotne oceny użytkowników, ale także prognozy dotyczące filmów, których każdy użytkownik nie widział. Na przykład ocena filmu Casablanca przez użytkownika 1 wynosiła 5,0. Produkt odpowiadający tej komórce w macierzy rekomendacji powinien mieć wartość około 5, 0.
(1.1 * 0.9) + (2.3 * 1.7) = 4.9Co ważniejsze, czy użytkownik 1 polubi film Czarna Pantera? Obliczenie iloczynu skalarnego odpowiadającego pierwszemu wierszowi i trzeciej kolumnie daje prognozowaną ocenę 4,3:
(1.1 * 1.4) + (2.3 * 1.2) = 4.3Rozkład macierzy zwykle daje macierz użytkowników i macierz produktów, które razem są znacznie bardziej kompaktowe niż macierz docelowa.
Średni błąd bezwzględny (MAE)
Średnia utrata na przykład, gdy używana jest utrata 1. Średni błąd bezwzględny obliczany jest w ten sposób:
- Obliczanie straty L1 dla partii.
- Podziel wartość funkcji straty L1 przez liczbę przykładów w partii.
Rozważmy na przykład obliczenie funkcji straty L1 na podstawie poniższej partii 5 przykładów:
| Rzeczywista wartość przykładu | Wartość prognozowana przez model | Strata (różnica między wartością rzeczywistą a przewidywaną) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = utrata L1 | ||
W tym przypadku wartość funkcji straty L1 wynosi 8, a liczba przykładów to 5. Średni błąd bezwzględny wynosi więc:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
Porównaj średni błąd bezwzględny z błędem średniokwadratowym i średnią kwadratową błędów.
średnia precyzja przy k (mAP@k),
Średnia statystyczna wszystkich wyników średniej precyzji przy k w zbiorze danych do weryfikacji. Średnia precyzja przy k jest używana do oceny jakości rekomendacji generowanych przez system rekomendacji.
Chociaż wyrażenie „średnia arytmetyczna” brzmi redundantnie, nazwa wskaźnika jest odpowiednia. W końcu ten wskaźnik oblicza średnią z wielu wartości średniej precyzji przy k.
Błąd średniokwadratowy (MSE)
Średnia utrata na przykład, gdy używana jest utrata 2. Oblicz błąd średniokwadratowy w ten sposób:
- Oblicz stratę L2 dla partii.
- Podziel utratę L2 przez liczbę przykładów w partii.
Rozważmy na przykład utratę w przypadku tej partii 5 przykładów:
| Rzeczywista wartość | Prognoza modelu | Strata | Strata kwadratowa |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L2 przegrana | |||
Dlatego błąd średniokwadratowy wynosi:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
Błąd średniokwadratowy to popularny optymalizator trenowania, szczególnie w przypadku regresji liniowej.
Porównaj błąd średniokwadratowy ze średnim błędem bezwzględnym i średnią kwadratową błędów.
TensorFlow Playground używa średniego błędu kwadratowego do obliczania wartości funkcji straty.
sieć typu mesh
W programowaniu równoległym ML termin związany z przypisywaniem danych i modelu do układów TPU oraz określaniem, jak te wartości będą dzielone lub replikowane.
Mesh to termin o wielu znaczeniach, który może oznaczać:
- Fizyczny układ układów TPU.
- Abstrakcyjna konstrukcja logiczna do mapowania danych i modelu na układy TPU.
W obu przypadkach siatka jest określana jako kształt.
meta-learning
Podzbiór uczenia maszynowego, który odkrywa lub ulepsza algorytm uczenia się. System meta-uczenia może też trenować model, aby szybko nauczył się nowego zadania na podstawie niewielkiej ilości danych lub doświadczenia zdobytego podczas poprzednich zadań. Algorytmy meta-uczenia zwykle próbują osiągnąć te cele:
- Ulepszanie lub poznawanie ręcznie zaprojektowanych funkcji (takich jak inicjator lub optymalizator).
- być bardziej wydajne pod względem danych i obliczeń,
- poprawić uogólnianie,
Meta-learning jest powiązany z uczeniem z małą liczbą przykładów.
wskaźnik
statystyka, na której Ci zależy;
Cel to wskaźnik, który system uczący się próbuje zoptymalizować.
Interfejs Metrics API (tf.metrics)
Interfejs TensorFlow API do oceny modeli. Na przykład tf.metrics.accuracy określa, jak często prognozy modelu są zgodne z etykietami.
mini-batch
Mały, losowo wybrany podzbiór partii przetwarzanej w ramach jednej iteracji. Rozmiar pakietu mini-pakietu wynosi zwykle od 10 do 1000 przykładów.
Załóżmy na przykład, że cały zbiór treningowy (pełna partia) składa się z 1000 przykładów. Załóżmy, że ustawisz rozmiar pakietu każdego mini-pakietu na 20. Dlatego w każdej iteracji określa utratę na podstawie losowych 20 przykładów z 1000, a następnie odpowiednio dostosowuje wagi i odchylenia.
Obliczanie funkcji straty na podstawie mini-wsadu jest znacznie wydajniejsze niż obliczanie jej na podstawie wszystkich przykładów w pełnym wsadzie.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
stochastyczny spadek wzdłuż gradientu w mini-partiach,
Algorytm gradientu prostego, który używa mini-batchów. Innymi słowy, mini-batch stochastic gradient descent szacuje gradient na podstawie małego podzbioru danych treningowych. Zwykłe stochastyczne zejście gradientowe używa mini-batcha o rozmiarze 1.
funkcja straty minimax
Funkcja straty dla generatywnych sieci przeciwstawnych na podstawie entropii krzyżowej między rozkładem wygenerowanych danych a rzeczywistych danych.
W pierwszym artykule opisującym generatywne sieci przeciwstawne użyto funkcji straty minimax.
Więcej informacji znajdziesz w sekcji Funkcje straty w kursie Generative Adversarial Networks.
klasa mniejszościowa,
Mniej popularna etykieta w zbiorze danych z nierównomiernym rozkładem klas. Na przykład w zbiorze danych zawierającym 99% etykiet negatywnych i 1% etykiet pozytywnych etykiety pozytywne stanowią klasę mniejszościową.
Kontrast z klasą większościową.
Więcej informacji znajdziesz w sekcji Zbiory danych: niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
model mieszanin ekspertów,
Schemat zwiększania wydajności sieci neuronowej przez używanie tylko podzbioru jej parametrów (nazywanego ekspertem) do przetwarzania danego wejściowego tokena lub przykładu. Sieć bramkująca kieruje każdy token wejściowy lub przykład do odpowiednich ekspertów.
Szczegółowe informacje znajdziesz w tych artykułach:
- Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer
- Mixture-of-Experts with Expert Choice Routing
ML
Skrót od uczenia maszynowego.
MMIT
Skrót od multimodal instruction-tuned.
MNIST
Zbiór danych w domenie publicznej opracowany przez LeCuna, Cortesa i Burgesa, który zawiera 60 tys. obrazów. Każdy z nich przedstawia sposób, w jaki człowiek ręcznie napisał konkretną cyfrę z zakresu 0–9. Każdy obraz jest przechowywany jako tablica 28x28 liczb całkowitych, gdzie każda liczba całkowita jest wartością w skali szarości z zakresu od 0 do 255 włącznie.
MNIST to kanoniczny zbiór danych do uczenia maszynowego, często używany do testowania nowych metod uczenia maszynowego. Więcej informacji znajdziesz w artykule The MNIST Database of Handwritten Digits.
modalność,
Kategoria danych najwyższego poziomu. Na przykład liczby, tekst, obrazy, filmy i dźwięk to 5 różnych rodzajów danych.
model
Ogólnie rzecz biorąc, jest to dowolna konstrukcja matematyczna, która przetwarza dane wejściowe i zwraca dane wyjściowe. Inaczej mówiąc, model to zestaw parametrów i struktury potrzebnych systemowi do tworzenia prognoz. W nadzorowanym uczeniu maszynowym model przyjmuje przykład jako dane wejściowe i wyciąga prognozę jako dane wyjściowe. W przypadku uczenia maszynowego z nadzorem modele nieco się różnią. Na przykład:
- Model regresji liniowej składa się z zestawu wag i wartości progowej.
- Model sieci neuronowej składa się z:
- Zestaw warstw ukrytych, z których każda zawiera co najmniej 1 neuron.
- wagi i odchylenia powiązane z każdym neuronem;
- Model drzewa decyzyjnego składa się z:
- Kształt drzewa, czyli wzorzec, w którym połączone są warunki i liście.
- Warunki i urlopy.
Możesz zapisywać, przywracać i kopiować modele.
Uczenie maszynowe bez nadzoru również generuje modele, zwykle funkcję, która może mapować przykładowe dane wejściowe na najbardziej odpowiednią grupę.
pojemność modelu,
Złożoność problemów, których model może się nauczyć. Im bardziej złożone problemy model może rozwiązywać, tym większa jest jego pojemność. Pojemność modelu zwykle rośnie wraz z liczbą jego parametrów. Formalną definicję pojemności modelu klasyfikacji znajdziesz w sekcji Wymiar VC.
kaskadowe modele
System, który wybiera idealny model dla konkretnego zapytania o wnioskowanie.
Wyobraź sobie grupę modeli, od bardzo dużych (z wieloma parametrami) po znacznie mniejsze (z dużo mniejszą liczbą parametrów). Bardzo duże modele zużywają więcej zasobów obliczeniowych w czasie wnioskowania niż mniejsze modele. Jednak bardzo duże modele mogą zwykle obsługiwać bardziej złożone żądania niż mniejsze modele. Kaskadowe modele określają złożoność zapytania o wnioskowanie, a następnie wybierają odpowiedni model do przeprowadzenia wnioskowania. Główną motywacją do stosowania kaskadowego modelu jest zmniejszenie kosztów wnioskowania przez wybieranie mniejszych modeli i używanie większych modeli tylko w przypadku bardziej złożonych zapytań.
Wyobraź sobie, że mały model działa na telefonie, a większa wersja tego modelu działa na serwerze zdalnym. Dobre kaskadowe modele obniżają koszty i opóźnienia, ponieważ mniejszy model może obsługiwać proste żądania, a model zdalny jest wywoływany tylko w przypadku złożonych żądań.
Zobacz też router modelu.
równoległość modelu,
Sposób skalowania trenowania lub wnioskowania, który polega na umieszczaniu różnych części jednego modelu na różnych urządzeniach. Równoległość modelu umożliwia korzystanie z modeli, które są zbyt duże, aby zmieścić się na jednym urządzeniu.
Aby wdrożyć równoległość modelu, system zwykle wykonuje te czynności:
- Dzieli model na mniejsze części.
- rozdziela trenowanie tych mniejszych części na wiele procesorów. Każdy procesor trenuje własną część modelu.
- łączy wyniki, aby utworzyć jeden model;
Równoległość modelu spowalnia trenowanie.
Zobacz też równoległość danych.
router modelu
Algorytm, który określa idealny model do wnioskowania w kaskadowym łączeniu modeli. Router modeli jest zwykle modelem uczenia maszynowego, który stopniowo uczy się wybierać najlepszy model dla danego wejścia. Router modeli może jednak czasami być prostszym algorytmem niezwiązanym z uczeniem maszynowym.
trenowanie modelu,
Proces określania najlepszego modelu.
MOE
Skrót od mixture of experts (mieszanka ekspertów).
Wykorzystanie chwili
Zaawansowany algorytm spadku gradientowego, w którym krok uczenia zależy nie tylko od pochodnej w bieżącym kroku, ale także od pochodnych kroków, które bezpośrednio go poprzedzały. Metoda momentum polega na obliczaniu wykładniczo ważonej średniej ruchomej gradientów w czasie, co jest analogiczne do pędu w fizyce. Momentum czasami zapobiega utknięciu uczenia w lokalnych minimach.
MT
Skrót od tłumaczenia maszynowego.
klasyfikacja wieloklasowa,
W uczeniu nadzorowanym problem klasyfikacji, w którym zbiór danych zawiera więcej niż 2 klasy etykiet. Na przykład etykiety w zbiorze danych Iris muszą należeć do jednej z tych 3 klas:
- Iris setosa
- Iris virginica
- Iris versicolor
Model wytrenowany na zbiorze danych Iris, który prognozuje typ irysa na podstawie nowych przykładów, wykonuje klasyfikację wieloklasową.
Z kolei problemy klasyfikacji, które rozróżniają dokładnie 2 klasy, są binarnymi modelami klasyfikacji. Na przykład model e-maila, który przewiduje, czy e-mail jest spamem, czy nie jest spamem, to model klasyfikacji binarnej.
W przypadku problemów z klastrowaniem klasyfikacja wieloklasowa odnosi się do więcej niż 2 klastrów.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: klasyfikacja wieloklasowa w kursie Machine Learning Crash Course.
wieloklasowa regresja logistyczna,
Używanie regresji logistycznej w problemach z klasyfikacją wieloklasową.
mechanizm wielogłowicowej uwagi
Rozszerzenie samouwagi, które stosuje mechanizm samouwagi wielokrotnie dla każdej pozycji w sekwencji wejściowej.
Transformery wprowadziły wielogłowicową uwagę własną.
dostosowany do instrukcji multimodalnych,
Model dostosowany do instrukcji, który może przetwarzać dane wejściowe inne niż tekst, takie jak obrazy, filmy i dźwięk.
model multimodalny,
Model, którego dane wejściowe, wyjściowe lub oba rodzaje danych obejmują więcej niż 1 rodzaj danych. Weźmy na przykład model, który jako cechy przyjmuje obraz i tekstowy podpis (2 rodzaje danych), a jako wynik podaje ocenę wskazującą, na ile tekstowy podpis pasuje do obrazu. Dane wejściowe tego modelu są multimodalne, a dane wyjściowe – unimodalne.
klasyfikacja wielomianowa,
Synonim klasyfikacji wieloklasowej.
regresja wielomianowa,
Synonim wieloklasowej regresji logistycznej.
wielozadaniowość
Technika uczenia maszynowego, w której jeden model jest trenowany do wykonywania wielu zadań.
Modele wielozadaniowe są tworzone przez trenowanie na danych odpowiednich dla każdego z różnych zadań. Dzięki temu model może nauczyć się udostępniać informacje między zadaniami, co pomaga mu skuteczniej się uczyć.
Model wytrenowany do wykonywania wielu zadań często ma lepsze możliwości generalizacji i może być bardziej odporny na różne typy danych.
N
Nano
Stosunkowo mały model Gemini przeznaczony do użytku na urządzeniu. Więcej informacji znajdziesz w sekcji Gemini Nano.
Pułapka NaN
Gdy podczas trenowania jedna z liczb w modelu stanie się wartością NaN, co spowoduje, że wiele lub wszystkie pozostałe liczby w modelu również staną się wartościami NaN.
NaN to skrót od Not a Number (nie liczba).
przetwarzanie języka naturalnego
Dziedzina nauczania komputerów przetwarzania tego, co użytkownik powiedział lub napisał, z użyciem reguł językowych. Prawie wszystkie nowoczesne systemy przetwarzania języka naturalnego opierają się na uczeniu maszynowym.rozumienie języka naturalnego
Podzbiór przetwarzania języka naturalnego, który określa intencje wypowiedzi lub tekstu. Rozumienie języka naturalnego może wykraczać poza przetwarzanie języka naturalnego i uwzględniać złożone aspekty języka, takie jak kontekst, sarkazm i nastawienie.
klasa wyników negatywnych,
W klasyfikacji binarnej jedna klasa jest określana jako pozytywna, a druga jako negatywna. Klasa pozytywna to rzecz lub zdarzenie, które model testuje, a klasa negatywna to inna możliwość. Na przykład:
- Klasa negatywna w teście medycznym może oznaczać „brak guza”.
- Klasa negatywna w modelu klasyfikacji e-maili może być oznaczona jako „nie spam”.
W przeciwieństwie do klasy wyników pozytywnych.
wykluczające próbkowanie
Synonim terminu próbkowanie kandydatów.
Neural Architecture Search (NAS)
Technika automatycznego projektowania architektury sieci neuronowej. Algorytmy NAS mogą skrócić czas i zmniejszyć zasoby potrzebne do trenowania sieci neuronowej.
NAS zwykle używa:
- Przestrzeń wyszukiwania, czyli zbiór możliwych architektur.
- funkcja oceny, która jest miarą tego, jak dobrze dana architektura radzi sobie z określonym zadaniem;
Algorytmy NAS często zaczynają od małego zbioru możliwych architektur i stopniowo rozszerzają przestrzeń wyszukiwania, gdy algorytm dowiaduje się więcej o tym, które architektury są skuteczne. Funkcja oceny jest zwykle oparta na skuteczności architektury w zbiorze treningowym, a algorytm jest zwykle trenowany przy użyciu techniki uczenia ze wzmocnieniem.
Algorytmy NAS okazały się skuteczne w znajdowaniu wydajnych architektur do różnych zadań, w tym klasyfikacji obrazów, klasyfikacji tekstu i tłumaczenia maszynowego.
sieć neuronowa
Model zawierający co najmniej 1 warstwę ukrytą. Głęboka sieć neuronowa to rodzaj sieci neuronowej zawierającej więcej niż jedną warstwę ukrytą. Na przykład poniższy diagram przedstawia głęboką sieć neuronową zawierającą 2 ukryte warstwy.
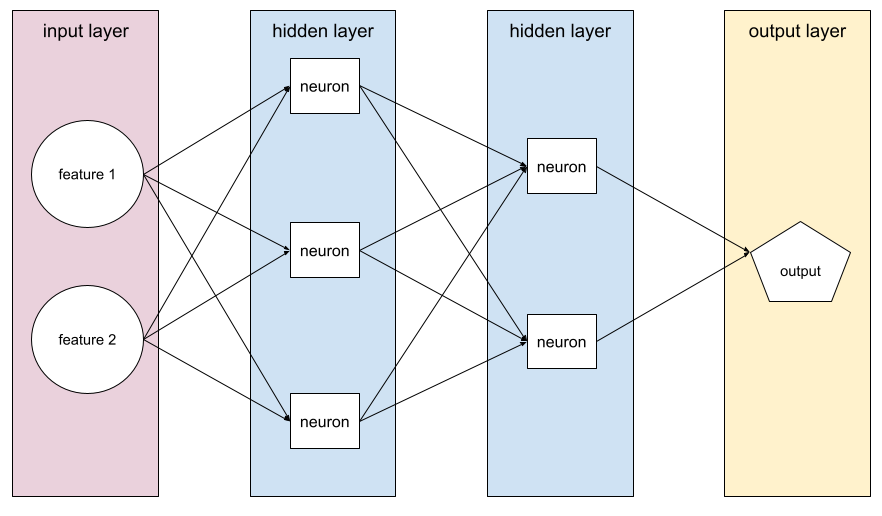
Każdy neuron w sieci neuronowej łączy się ze wszystkimi węzłami w następnej warstwie. Na przykład na powyższym diagramie widać, że każdy z 3 neuronów w pierwszej warstwie ukrytej jest połączony oddzielnie z każdym z 2 neuronów w drugiej warstwie ukrytej.
Sieci neuronowe zaimplementowane na komputerach są czasami nazywane sztucznymi sieciami neuronowymi, aby odróżnić je od sieci neuronowych występujących w mózgu i innych układach nerwowych.
Niektóre sieci neuronowe mogą naśladować bardzo złożone nieliniowe zależności między różnymi cechami a etykietą.
Zobacz też splotową sieć neuronową i rekurencyjną sieć neuronową.
Więcej informacji znajdziesz w sekcji Sieci neuronowe w Szybkim szkoleniu z uczenia maszynowego.
neuron,
W uczeniu maszynowym jest to odrębna jednostka w warstwie ukrytej sieci neuronowej. Każdy neuron wykonuje te 2 czynności:
- Oblicza sumę ważoną wartości wejściowych pomnożonych przez odpowiednie wagi.
- Przekazuje sumę ważoną jako dane wejściowe do funkcji aktywacji.
Neuron w pierwszej warstwie ukrytej przyjmuje dane wejściowe z wartości cech w warstwie wejściowej. Neuron w dowolnej warstwie ukrytej za pierwszą przyjmuje dane wejściowe z neuronów w poprzedniej warstwie ukrytej. Na przykład neuron w 2. warstwie ukrytej przyjmuje dane wejściowe z neuronów w 1. warstwie ukrytej.
Ilustracja poniżej przedstawia 2 neurony i ich dane wejściowe.
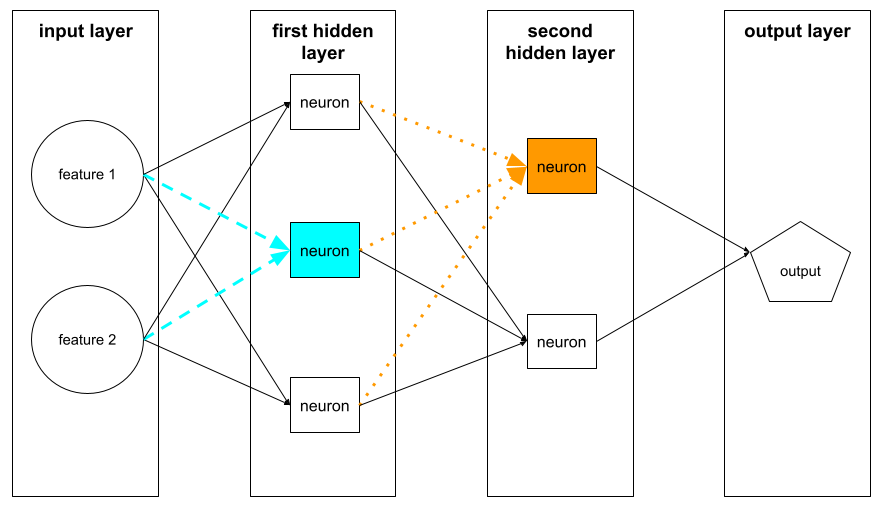
Neuron w sieci neuronowej naśladuje zachowanie neuronów w mózgu i innych częściach układu nerwowego.
N-gram
Uporządkowana sekwencja N słów. Na przykład truly madly to 2-gram. Ponieważ kolejność ma znaczenie, madly truly to inny 2-gram niż truly madly.
| N | Nazwy tego rodzaju n-gramu | Przykłady |
|---|---|---|
| 2 | bigram lub 2-gram | iść, jeść obiad, jeść kolację |
| 3 | trigram lub 3-gram | zjadł za dużo, żyli długo i szczęśliwie, bije dzwon |
| 4 | 4-gramowy | spacer w parku, pył na wietrze, chłopiec zjadł soczewicę |
Wiele modeli rozumienia języka naturalnego opiera się na n-gramach, aby przewidywać kolejne słowo, które użytkownik wpisze lub wypowie. Załóżmy na przykład, że użytkownik wpisał i żyli długo i szczęśliwie. Model NLU oparty na trigramach prawdopodobnie przewidzi, że użytkownik wpisze słowo po.
Porównaj n-gramy z workiem słów, czyli nieuporządkowanymi zbiorami słów.
Więcej informacji znajdziesz w sekcji Duże modele językowe w szybkim szkoleniu z uczenia maszynowego.
NLP
Skrót od przetwarzania języka naturalnego.
NLU
Skrót od rozumienia języka naturalnego.
węzeł (drzewo decyzyjne)
W drzewie decyzyjnym dowolny warunek lub węzeł.
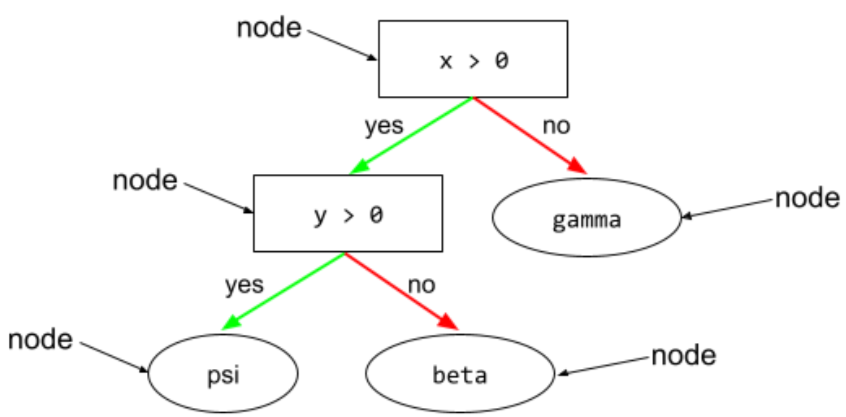
Więcej informacji znajdziesz w schematach decyzyjnych w kursie Decision Forests.
węzeł (sieć neuronowa)
Więcej informacji znajdziesz w sekcji Sieci neuronowe w Szybkim szkoleniu z uczenia maszynowego.
węzeł (graf TensorFlow)
Operacja w grafie TensorFlow.
szum
Ogólnie rzecz biorąc, wszystko, co zaciemnia sygnał w zbiorze danych. Szum może być wprowadzany do danych na różne sposoby. Na przykład:
- Osoby oceniające popełniają błędy podczas oznaczania etykietami.
- Ludzie i urządzenia mogą błędnie rejestrować lub pomijać wartości cech.
warunek niebinarny
Warunek zawierający więcej niż 2 możliwe wyniki. Na przykład poniższy warunek niebinarny ma 3 możliwe wyniki:
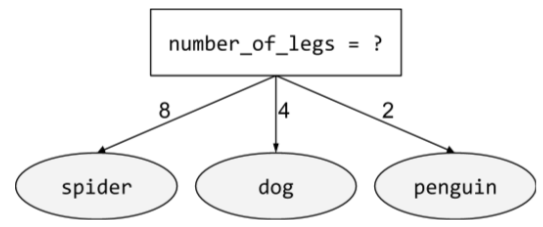
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
nieliniowy,
Zależność między dwiema lub większą liczbą zmiennych, której nie można przedstawić wyłącznie za pomocą dodawania i mnożenia. Relację liniową można przedstawić jako linię, a relacji nieliniowej nie można. Rozważmy na przykład 2 modele, z których każdy wiąże jedną cechę z jedną etykietą. Model po lewej stronie jest liniowy, a model po prawej stronie jest nieliniowy:

W sekcji Sieci neuronowe: węzły i warstwy ukryte w kursie Machine Learning Crash Course możesz eksperymentować z różnymi rodzajami funkcji nieliniowych.
błąd braku odpowiedzi,
Zobacz błąd doboru.
niestacjonarność
Cecha, której wartości zmieniają się w co najmniej 1 wymiarze, zwykle w czasie. Oto przykłady niestacjonarności:
- Liczba sprzedanych kostiumów kąpielowych w danym sklepie różni się w zależności od sezonu.
- Ilość określonego owocu zebranego w danym regionie jest przez większą część roku zerowa, ale przez krótki okres bardzo duża.
- Ze względu na zmiany klimatu średnie roczne temperatury ulegają zmianie.
Kontrast z stacjonarnością.
brak jednej prawidłowej odpowiedzi (NORA)
Prompt z wieloma prawidłowymi odpowiedziami. Na przykład ten prompt nie ma jednej prawidłowej odpowiedzi:
Opowiedz mi zabawny dowcip o słoniach.
Ocena odpowiedzi na prompty, które nie mają jednej prawidłowej odpowiedzi, jest zwykle znacznie bardziej subiektywna niż ocena promptów, które mają jedną prawidłową odpowiedź. Na przykład ocena żartu o słoniu wymaga systematycznego sposobu określania, jak śmieszny jest dany żart.
NORA
Skrót od no one right answer (nie ma jednej prawidłowej odpowiedzi).
normalizacja,
Ogólnie rzecz biorąc, proces przekształcania rzeczywistego zakresu wartości zmiennej w standardowy zakres wartości, np.:
- -1 do +1
- Od 0 do 1
- Wyniki z (w przybliżeniu od -3 do +3)
Załóżmy na przykład, że rzeczywisty zakres wartości pewnej cechy to 800–2400. W ramach inżynierii cech możesz znormalizować rzeczywiste wartości do standardowego zakresu, np. od -1 do +1.
Normalizacja to powszechne zadanie w inżynierii cech. Modele zwykle trenują szybciej (i generują lepsze prognozy), gdy każda cecha numeryczna w wektorze cech ma mniej więcej ten sam zakres.
Zobacz też normalizację wyniku z.
Więcej informacji znajdziesz w sekcji Dane liczbowe: normalizacja w kursie Machine Learning Crash Course.
Notebook LM
Narzędzie oparte na Gemini, które umożliwia użytkownikom przesyłanie dokumentów, a następnie zadawanie pytań, podsumowywanie i organizowanie tych dokumentów za pomocą promptów. Na przykład autor może przesłać kilka opowiadań i poprosić NotebookLM o znalezienie wspólnych motywów lub określenie, które z nich najlepiej nadaje się na film.
wykrywanie nowości,
Proces określania, czy nowy (nieznany) przykład pochodzi z tego samego rozkładu co zbiór treningowy. Innymi słowy, po wytrenowaniu na zbiorze treningowym wykrywanie nowości określa, czy nowy przykład (podczas wnioskowania lub dodatkowego trenowania) jest wartością odstającą.
Porównaj z wykrywaniem wyników odstających.
dane liczbowe,
Cechy reprezentowane jako liczby całkowite lub rzeczywiste. Na przykład model wyceny domu prawdopodobnie będzie reprezentować wielkość domu (w stopach lub metrach kwadratowych) jako dane liczbowe. Przedstawienie cechy jako danych liczbowych oznacza, że wartości cechy mają matematyczny związek z etykietą. Oznacza to, że liczba metrów kwadratowych w domu prawdopodobnie ma pewien związek matematyczny z jego wartością.
Nie wszystkie dane całkowite powinny być reprezentowane jako dane liczbowe. Na przykład kody pocztowe w niektórych częściach świata są liczbami całkowitymi, ale nie powinny być reprezentowane w modelach jako dane liczbowe. Dzieje się tak, ponieważ kod pocztowy 20000 nie jest 2 razy (ani o połowę) skuteczniejszy niż kod pocztowy 10000. Ponadto, chociaż różne kody pocztowe są powiązane z różnymi wartościami nieruchomości, nie możemy zakładać, że wartości nieruchomości w przypadku kodu pocztowego 20000 są 2 razy większe niż w przypadku kodu pocztowego 10000.
Kody pocztowe powinny być reprezentowane jako dane jakościowe.
Cechy liczbowe są czasami nazywane cechami ciągłymi.
Więcej informacji znajdziesz w sekcji Praca z danymi liczbowymi w kursie Machine Learning Crash Course.
NumPy
Biblioteka matematyczna typu open source zapewniająca wydajne operacje na tablicach w Pythonie.pandas jest oparta na NumPy.
O
cel
Wskaźnik, który algorytm próbuje zoptymalizować.
funkcja celu
Formuła matematyczna lub dane, które model ma optymalizować. Na przykład funkcja celu w przypadku regresji liniowej to zwykle średnia kwadratowa strata. Dlatego podczas trenowania modelu regresji liniowej celem jest zminimalizowanie straty średniokwadratowej.
W niektórych przypadkach celem jest maksymalizacja funkcji celu. Jeśli np. funkcja celu to dokładność, celem jest jej maksymalizacja.
Zobacz też utratę.
warunek ukośny
W drzewie decyzyjnym warunek, który obejmuje więcej niż 1 cechę. Jeśli np. wysokość i szerokość są cechami, warunek ukośny może wyglądać tak:
height > width
Porównaj z warunkiem wyrównanym do osi.
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
offline
Synonim słowa static.
wnioskowanie offline,
Proces generowania przez model partii prognoz i następnie zapisywania ich w pamięci podręcznej. Aplikacje mogą wtedy uzyskać dostęp do wywnioskowanej prognozy z pamięci podręcznej, zamiast ponownie uruchamiać model.
Rozważmy na przykład model, który generuje lokalne prognozy pogody (prognozy) co 4 godziny. Po każdym uruchomieniu modelu system zapisuje w pamięci podręcznej wszystkie lokalne prognozy pogody. Aplikacje pogodowe pobierają prognozy z pamięci podręcznej.
Wnioskowanie offline jest też nazywane wnioskowaniem statycznym.
Kontrast z wnioskowaniem online. Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: wnioskowanie statyczne a dynamiczne w kursie Machine Learning Crash Course.
kodowanie 1 z n,
Przedstawianie danych kategorialnych jako wektora, w którym:
- Jeden element jest ustawiony na 1.
- Wszystkie pozostałe elementy są ustawione na 0.
Kodowanie 1-z-N jest często używane do reprezentowania ciągów znaków lub identyfikatorów, które mają skończony zbiór możliwych wartości.
Załóżmy na przykład, że pewna cecha kategorialna o nazwie Scandinavia ma 5 możliwych wartości:
- „Dania”
- „Szwecja”
- „Norwegia”
- „Finlandia”
- „Islandia”
Kodowanie 1-z-N może przedstawiać każdą z 5 wartości w ten sposób:
| Kraj | Wektor | ||||
|---|---|---|---|---|---|
| „Dania” | 1 | 0 | 0 | 0 | 0 |
| „Szwecja” | 0 | 1 | 0 | 0 | 0 |
| „Norwegia” | 0 | 0 | 1 | 0 | 0 |
| „Finlandia” | 0 | 0 | 0 | 1 | 0 |
| „Islandia” | 0 | 0 | 0 | 0 | 1 |
Dzięki kodowaniu 1-z-N model może nauczyć się różnych połączeń na podstawie każdego z 5 krajów.
Przedstawienie cechy jako danych liczbowych jest alternatywą dla kodowania 1 z n. Niestety przedstawianie krajów skandynawskich w formie liczbowej nie jest dobrym pomysłem. Na przykład:
- „Dania” to 0
- „Szwecja” to 1
- „Norwegia” to 2
- „Finland” to 3
- „Islandia” to 4
W przypadku kodowania numerycznego model interpretuje surowe liczby matematycznie i próbuje trenować na ich podstawie. Jednak Islandia nie jest w rzeczywistości 2 razy większa (ani 2 razy mniejsza) od Norwegii, więc model wyciągnąłby dziwne wnioski.
Więcej informacji znajdziesz w sekcji Dane kategorialne: słownictwo i kodowanie 1-z-N w kursie Machine Learning Crash Course.
jedna prawidłowa odpowiedź (ORA),
Prompt z jedną prawidłową odpowiedzią. Rozważmy na przykład ten prompt:
Prawda czy fałsz: Saturn jest większy od Marsa.
Jedyną prawidłową odpowiedzią jest prawda.
W przeciwieństwie do nie ma jednej prawidłowej odpowiedzi.
uczenie jednokrotne,
Podejście oparte na uczeniu maszynowym, często stosowane do klasyfikacji obiektów, zaprojektowane tak, aby na podstawie jednego przykładu szkoleniowego nauczyć się skutecznego modelu klasyfikacji.
Zobacz też uczenie „few-shot” i uczenie „zero-shot”.
prompty „one-shot”
Prompt zawierający jeden przykład pokazujący, jak powinien odpowiadać duży model językowy. Na przykład poniższy prompt zawiera 1 przykład pokazujący dużemu modelowi językowemu, jak powinien odpowiadać na zapytanie.
| Elementy jednego promptu | Uwagi |
|---|---|
| Jaka jest oficjalna waluta w wybranym kraju? | Pytanie, na które ma odpowiedzieć LLM. |
| Francja: EUR | Przykład. |
| Indie: | Faktyczne zapytanie. |
Porównaj promptowanie z jednym przykładem z tymi terminami:
jeden kontra reszta
W przypadku problemu klasyfikacji z N klasami rozwiązanie składające się z N osobnych modeli klasyfikacji binarnej – po jednym modelu klasyfikacji binarnej dla każdego możliwego wyniku. Na przykład w przypadku modelu, który klasyfikuje przykłady jako zwierzę, roślinę lub minerał, rozwiązanie typu „jeden kontra reszta” zapewni te 3 osobne binarne modele klasyfikacji:
- zwierzę lub nie zwierzę,
- warzywo a nie warzywo,
- mineralne lub nie
online
Synonim słowa dynamiczny.
wnioskowanie online,
Generowanie prognoz na żądanie. Załóżmy na przykład, że aplikacja przekazuje dane wejściowe do modelu i wysyła żądanie prognozy. System korzystający z wnioskowania online odpowiada na żądanie, uruchamiając model (i zwracając prognozę do aplikacji).
W przeciwieństwie do wnioskowania offline.
Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: wnioskowanie statyczne a dynamiczne w kursie Machine Learning Crash Course.
operacja (op)
W TensorFlow każda procedura, która tworzy, modyfikuje lub usuwa Tensor. Na przykład mnożenie macierzy to operacja, która przyjmuje 2 tensory jako dane wejściowe i generuje 1 tensor jako dane wyjściowe.
Optax
Biblioteka do przetwarzania i optymalizacji gradientów dla JAX. Optax ułatwia badania, udostępniając elementy składowe, które można łączyć w niestandardowy sposób w celu optymalizacji modeli parametrycznych, takich jak głębokie sieci neuronowe. Inne cele to:
- zapewnianie czytelnych, dobrze przetestowanych i wydajnych implementacji podstawowych komponentów;
- zwiększa produktywność, umożliwiając łączenie składników niskiego poziomu w niestandardowe optymalizatory (lub inne komponenty przetwarzania gradientowego);
- Przyspieszanie wdrażania nowych pomysłów poprzez ułatwianie wszystkim osobom wnoszenia wkładu.
optymalizator,
Konkretna implementacja algorytmu spadku wzdłuż gradientu. Popularne optymalizatory to:
- AdaGrad, czyli ADAptive GRADient descent (adaptacyjna metoda gradientu prostego).
- Adam, czyli ADAptive with Momentum.
ORA
Skrót oznaczający jedną poprawną odpowiedź.
błąd jednorodności grupy obcej,
Tendencja do postrzegania członków grupy obcej jako bardziej podobnych do siebie niż członków grupy własnej podczas porównywania postaw, wartości, cech osobowości i innych charakterystyk. Grupa własna to osoby, z którymi regularnie się kontaktujesz; grupa obca to osoby, z którymi nie kontaktujesz się regularnie. Jeśli poprosisz osoby o podanie atrybutów dotyczących grup zewnętrznych, mogą one być mniej zniuansowane i bardziej stereotypowe niż atrybuty, które uczestnicy wymieniają w przypadku osób z ich grupy wewnętrznej.
Na przykład Lilipuci mogą szczegółowo opisywać domy innych Liliputów, podając niewielkie różnice w stylach architektonicznych, oknach, drzwiach i rozmiarach. Jednak ci sami Lilipuci mogą po prostu stwierdzić, że wszyscy Brobdingnagowie mieszkają w identycznych domach.
Błąd jednorodności grupy obcej to forma błędu uogólnienia.
Zobacz też stronniczość wewnątrzgrupową.
wykrywanie wyników odstających,
Proces identyfikowania elementów odstających w zbiorze treningowym.
Porównaj z wykrywaniem nowości.
nietypowych danych
Wartości znacznie odbiegające od większości pozostałych wartości. W uczeniu maszynowym do wartości odstających zaliczamy:
- Dane wejściowe, których wartości różnią się od średniej o więcej niż około 3 odchylenia standardowe.
- Wagi o wysokich wartościach bezwzględnych.
- Wartości prognozowane są stosunkowo odległe od rzeczywistych.
Załóżmy na przykład, że widget-price jest cechą określonego modelu.
Załóżmy, że średnia widget-price wynosi 7 euro, a odchylenie standardowe to 1 euro. Przykłady zawierające widget-price w wysokości 12 PLN lub 2 PLN byłyby zatem uznawane za wartości odstające, ponieważ każda z tych cen jest oddalona od średniej o 5 odchyleń standardowych.
Wartości odstające są często spowodowane literówkami lub innymi błędami wprowadzania. W innych przypadkach wartości odstające nie są błędami. W końcu wartości oddalone o 5 odchyleń standardowych od średniej są rzadkie, ale nie niemożliwe.
Wartości odstające często powodują problemy podczas trenowania modelu. Obcinanie to jeden ze sposobów zarządzania wartościami odstającymi.
Więcej informacji znajdziesz w sekcji Praca z danymi liczbowymi w kursie Machine Learning Crash Course.
ocena poza próbą (OOB)
Mechanizm oceny jakości lasu decyzyjnego przez testowanie każdego drzewa decyzyjnego na przykładach, które nie były używane podczas trenowania tego drzewa decyzyjnego. Na przykład na poniższym diagramie widać, że system trenuje każde drzewo decyzyjne na około 2/3 przykładów, a następnie ocenia je na pozostałej 1/3 przykładów.
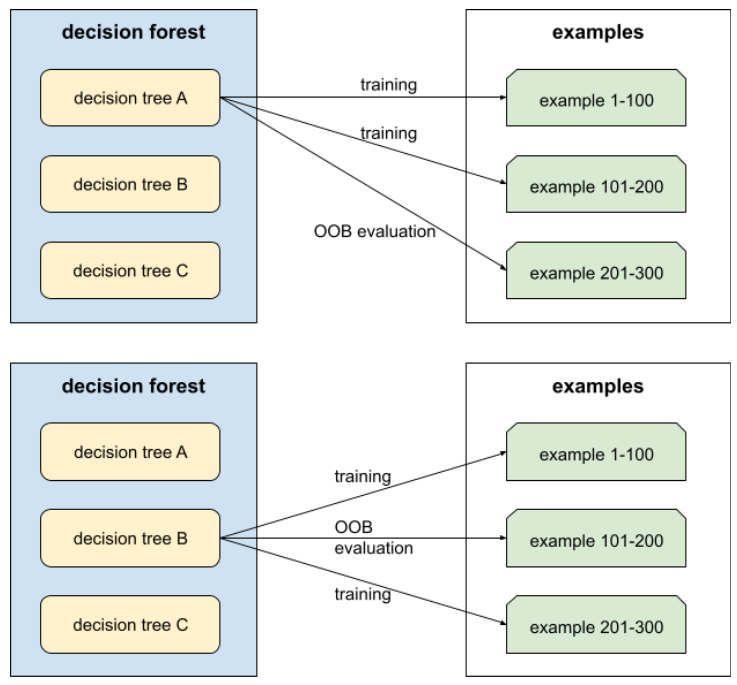
Ocena poza próbą jest wydajnym obliczeniowo i konserwatywnym przybliżeniem mechanizmu walidacji krzyżowej. W przypadku weryfikacji krzyżowej trenowany jest jeden model w każdej rundzie weryfikacji krzyżowej (np. w 10-krotnej weryfikacji krzyżowej trenowanych jest 10 modeli). W przypadku oceny OOB trenowany jest jeden model. Ponieważ bagging podczas trenowania każdego drzewa pomija część danych, ocena OOB może wykorzystać te dane do przybliżonego przeprowadzenia walidacji krzyżowej.
Więcej informacji znajdziesz w sekcji Ocena poza próbą w kursie Decision Forests.
warstwa wyjściowa,
„Ostatnia” warstwa sieci neuronowej. Warstwa wyjściowa zawiera prognozę.
Ilustracja poniżej przedstawia małą głęboką sieć neuronową z warstwą wejściową, 2 warstwami ukrytymi i warstwą wyjściową:
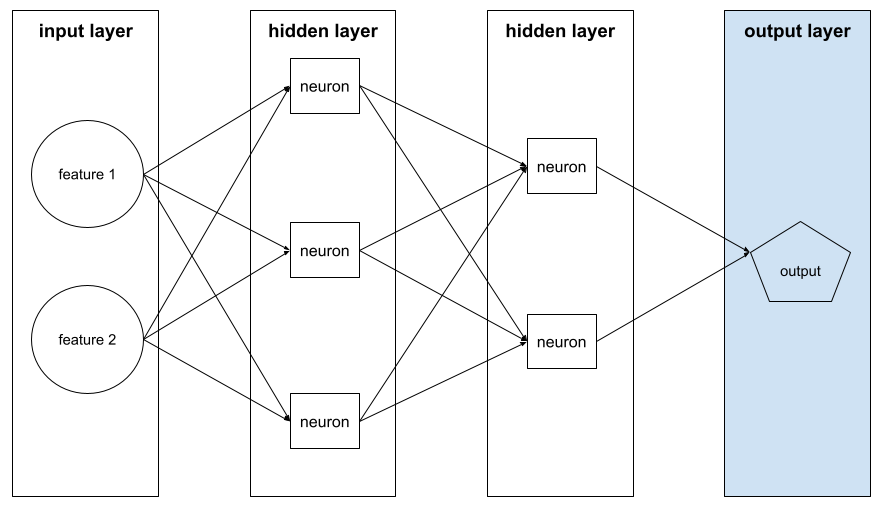
nadmierne dopasowanie
Tworzenie modelu, który jest tak ściśle dopasowany do danych treningowych, że nie jest w stanie dokonywać prawidłowych prognoz na podstawie nowych danych.
Regularyzacja może zmniejszyć przeuczenie. Trenowanie na dużym i zróżnicowanym zbiorze treningowym może również zmniejszyć przeuczenie.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie w szybkim szkoleniu z uczenia maszynowego.
nadpróbkowanie
Ponowne wykorzystanie przykładów klasy mniejszościowej w zbiorze danych z niezrównoważonymi klasami w celu utworzenia bardziej zrównoważonego zbioru treningowego.
Rozważmy na przykład problem klasyfikacji binarnej, w którym stosunek klasy większościowej do klasy mniejszościowej wynosi 5000:1. Jeśli zbiór danych zawiera milion przykładów, to w przypadku klasy mniejszościowej jest to tylko około 200 przykładów, co może być zbyt małą liczbą do skutecznego trenowania. Aby przezwyciężyć ten niedobór, możesz wielokrotnie nadpróbkować (ponownie wykorzystać) te 200 przykładów, co może dać wystarczającą liczbę przykładów do skutecznego trenowania.
Podczas nadpróbkowania musisz uważać na nadmierne dopasowanie.
Kontrastuje to z niedosamplowaniem.
P
spakowane dane,
Metoda wydajniejszego przechowywania danych.
Spakowane dane są przechowywane w formacie skompresowanym lub w inny sposób, który umożliwia bardziej efektywny dostęp do nich. Spakowane dane minimalizują ilość pamięci i obliczeń wymaganych do uzyskania do nich dostępu, co przyspiesza trenowanie i zwiększa wydajność wnioskowania modelu.
Spakowane dane są często używane z innymi technikami, takimi jak rozszerzanie danych i regularyzacja, co dodatkowo zwiększa wydajność modeli.
PaLM
Skrót od Pathways Language Model.
pandy
Interfejs API do analizy danych zorientowany na kolumny, oparty na bibliotece numpy. Wiele platform uczenia maszynowego, w tym TensorFlow, obsługuje struktury danych pandas jako dane wejściowe. Szczegóły znajdziesz w dokumentacji biblioteki pandas.
parametr
Wagi i odchylenia, których model uczy się podczas trenowania. Na przykład w modelu regresji liniowej parametry to wyraz wolny (b) i wszystkie wagi (w1, w2 itd.) w tej formule:
Natomiast hiperparametry to wartości, które Ty (lub usługa dostrajania hiperparametrów) przekazujesz do modelu. Na przykład szybkość uczenia się jest hiperparametrem.
dostrajanie konkretnych parametrów,
Zbiór technik dostrajania dużego wstępnie wytrenowanego modelu językowego (PLM) w sposób bardziej efektywny niż pełne dostrajanie. Dostrajanie konkretnych parametrów zwykle dostraja znacznie mniej parametrów niż pełne dostrajanie, ale zwykle tworzy duży model językowy, który działa tak samo (lub prawie tak samo) jak duży model językowy utworzony na podstawie pełnego dostrajania.
Porównaj dostrajanie konkretnych parametrów z:
Dostrajanie konkretnych parametrów jest też nazywane dostrajaniem konkretnych parametrów.
Serwer parametrów (PS)
Zadanie, które śledzi parametry modelu w środowisku rozproszonym.
aktualizacja parametru,
Operacja dostosowywania parametrów modelu podczas trenowania, zwykle w ramach jednej iteracji metody gradientu prostego.
pochodna cząstkowa
Pochodna, w której wszystkie zmienne z wyjątkiem jednej są traktowane jako stałe. Na przykład pochodna cząstkowa funkcji f(x, y) względem x to pochodna funkcji f traktowanej jako funkcja tylko zmiennej x (czyli przy założeniu, że y jest stałe). Pochodna cząstkowa funkcji f względem x uwzględnia tylko zmianę x i ignoruje wszystkie inne zmienne w równaniu.
błąd związany z udziałem w badaniu
Synonim błędu braku odpowiedzi. Zobacz błąd doboru.
strategia partycjonowania,
Algorytm, według którego zmienne są dzielone między serwery parametrów.
pass at k (pass@k)
Metryka określająca jakość kodu (np. w języku Python) generowanego przez duży model językowy. W szczególności wartość k informuje o prawdopodobieństwie, że co najmniej 1 z k wygenerowanych bloków kodu przejdzie wszystkie testy jednostkowe.
Duże modele językowe często mają trudności z generowaniem dobrego kodu w przypadku złożonych problemów programistycznych. Inżynierowie oprogramowania radzą sobie z tym problemem, prosząc duży model językowy o wygenerowanie wielu (k) rozwiązań tego samego problemu. Następnie inżynierowie oprogramowania testują każde rozwiązanie za pomocą testów jednostkowych. Obliczenie wyniku testu na poziomie k zależy od wyników testów jednostkowych:
- Jeśli co najmniej jedno z tych rozwiązań przejdzie test jednostkowy, LLM przejdzie to wyzwanie związane z generowaniem kodu.
- Jeśli żadne z rozwiązań nie przejdzie testu jednostkowego, LLM nie zaliczy tego zadania związanego z generowaniem kodu.
Formuła dla przepustki na poziomie k wygląda tak:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
Ogólnie wyższe wartości k dają wyższe wyniki testu Pass@k, ale wymagają większych zasobów dużego modelu językowego i testów jednostkowych.
Model językowy PaLM
Starszy model i poprzednik modeli Gemini.
Pax
Platforma programistyczna przeznaczona do trenowania dużych modeli sieci neuronowych , które są tak duże, że obejmują wiele układów TPU, akceleratorów lub podów.
Pax jest oparty na Flax, który z kolei jest oparty na JAX.
perceptron
System (sprzętowy lub programowy), który przyjmuje co najmniej jedną wartość wejściową, wykonuje funkcję na ważonej sumie danych wejściowych i oblicza pojedynczą wartość wyjściową. W uczeniu maszynowym funkcja jest zwykle nieliniowa, np. ReLU, sigmoid lub tanh. Na przykład ten perceptron wykorzystuje funkcję sigmoid do przetwarzania 3 wartości wejściowych:
Na ilustracji poniżej perceptron przyjmuje 3 dane wejściowe, z których każde jest modyfikowane przez wagę przed wejściem do perceptronu:

Perceptrony to neurony w sieciach neuronowych.
występ
Termin o wielu znaczeniach:
- Standardowe znaczenie w inżynierii oprogramowania. Chodzi o to, jak szybko (lub wydajnie) działa to oprogramowanie.
- Znaczenie w uczeniu maszynowym. Skuteczność odpowiada na pytanie: jak dokładny jest ten model? Czyli jak dobre są prognozy modelu?
permutacyjna ważność zmiennych
Rodzaj znaczenia zmiennej, który ocenia wzrost błędu prognozy modelu po przestawieniu wartości cechy. Permutacyjna ważność zmiennych to niezależny od modelu wskaźnik.
perplexity
Miara tego, jak dobrze model wykonuje swoje zadanie. Załóżmy na przykład, że Twoim zadaniem jest odczytanie kilku pierwszych liter słowa, które użytkownik wpisuje na klawiaturze telefonu, i zaproponowanie listy możliwych słów do dokończenia. Złożoność P w tym przypadku to w przybliżeniu liczba propozycji, które musisz podać, aby na liście znalazło się słowo, które użytkownik próbuje wpisać.
Złożoność jest powiązana z entropią krzyżową w ten sposób:
potok
Infrastruktura związana z algorytmem uczenia maszynowego. Proces obejmuje zbieranie danych, umieszczanie ich w plikach danych treningowych, trenowanie co najmniej jednego modelu i eksportowanie modeli do środowiska produkcyjnego.
Więcej informacji znajdziesz w module Potoki ML w kursie Zarządzanie projektami ML.
potokowanie
Rodzaj równoległości modelu, w której przetwarzanie modelu jest dzielone na kolejne etapy, a każdy etap jest wykonywany na innym urządzeniu. Gdy etap przetwarza jedną partię, poprzedni etap może pracować nad następną partią.
Zobacz też szkolenie etapowe.
pjit
Funkcja JAX, która dzieli kod, aby można go było uruchamiać na wielu chipach akceleratora. Użytkownik przekazuje funkcję do pjit, która zwraca funkcję o równoważnej semantyce, ale skompilowaną do obliczeń XLA, które są wykonywane na wielu urządzeniach (takich jak procesory graficzne lub rdzenie TPU).
pjit umożliwia użytkownikom dzielenie obliczeń bez ich przepisywania za pomocą partycjonera SPMD.
Od marca 2023 r. usługa pjit została połączona z usługą jit. Więcej informacji znajdziesz w artykule Rozproszone tablice i automatyczna paralelizacja.
PLM
Skrót od wytrenowanego modelu językowego.
pmap
Funkcja JAX, która wykonuje kopie funkcji wejściowej na wielu urządzeniach sprzętowych (procesorach, GPU lub TPU) z różnymi wartościami wejściowymi. Funkcja pmap opiera się na SPMD.
zasada
W uczeniu przez wzmacnianie agent to probabilistyczne mapowanie stanów na działania.
pooling
Zmniejszanie macierzy (lub macierzy) utworzonej przez wcześniejszą warstwę konwolucyjną do mniejszej macierzy. Łączenie zwykle polega na przyjęciu wartości maksymalnej lub średniej na obszarze połączonym. Załóżmy na przykład, że mamy macierz 3x3:
![Macierz 3x3 [[5,3,1], [8,2,5], [9,4,3]].](https://developers.google.cn/static/machine-learning/glossary/images/PoolingStart.svg?authuser=00&hl=pl)
Operacja łączenia, podobnie jak operacja splotu, dzieli tę macierz na wycinki, a następnie przesuwa operację splotu o kroki. Załóżmy na przykład, że operacja łączenia dzieli macierz splotową na wycinki 2x2 z krokiem 1x1. Jak widać na poniższym diagramie, wykonywane są 4 operacje łączenia w pule. Załóżmy, że każda operacja łączenia wybiera maksymalną wartość z 4 w danym wycinku:
![Macierz wejściowa ma wymiary 3x3 i zawiera wartości: [[5,3,1], [8,2,5], [9,4,3]].
Lewy górny podblok 2x2 macierzy wejściowej to [[5,3], [8,2]], więc
operacja łączenia w lewym górnym rogu daje wartość 8 (czyli
maksimum z 5, 3, 8 i 2). Prawa górna podmacierz 2x2 macierzy wejściowej to [[3,1], [2,5]], więc operacja puli w prawym górnym rogu daje wartość 5. Lewy dolny podblok macierzy wejściowej o rozmiarach 2x2 to [[8,2], [9,4]], więc operacja łączenia w pule w lewym dolnym rogu daje wartość 9. Prawa dolna podmacierz wejściowej macierzy 2x2 to [[2,5], [4,3]], więc operacja łączenia w prawa dolna podmacierzy daje wartość 5. Podsumowując, operacja łączenia w pule daje macierz 2x2 [[8,5], [9,5]].](https://developers.google.cn/static/machine-learning/glossary/images/PoolingConvolution.svg?authuser=00&hl=pl)
Pooling pomaga wymusić niezmienność tłumaczenia w macierzy wejściowej.
Pooling w przypadku aplikacji do przetwarzania obrazu jest bardziej formalnie nazywany poolingiem przestrzennym. W przypadku aplikacji z szeregami czasowymi pooling jest zwykle nazywany poolingiem czasowym. Nieformalnie pooling jest często nazywany podpróbkowaniem lub próbkowaniem w dół.
Więcej informacji znajdziesz w artykule Wprowadzenie do konwolucyjnych sieci neuronowych w kursie ML Practicum: Image Classification.
kodowanie pozycyjne,
Metoda dodawania informacji o pozycji tokena w sekwencji do jego osadzania. Modele Transformer wykorzystują kodowanie pozycyjne, aby lepiej zrozumieć relacje między różnymi częściami sekwencji.
Typowa implementacja kodowania pozycyjnego wykorzystuje funkcję sinusoidalną. (Częstotliwość i amplituda funkcji sinusoidalnej są określane przez pozycję tokena w sekwencji). Ta technika umożliwia modelowi Transformer uczenie się, jak zwracać uwagę na różne części sekwencji na podstawie ich pozycji.
klasa wyników pozytywnych,
Klasa, dla której przeprowadzasz test.
Na przykład klasą pozytywną w modelu do wykrywania raka może być „guz”. Klasą pozytywną w modelu klasyfikacji e-maili może być „spam”.
Porównaj z klasą wyników negatywnych.
przetwarzanie końcowe,
Dostosowywanie danych wyjściowych modelu po jego uruchomieniu. Przetwarzanie końcowe może służyć do egzekwowania ograniczeń dotyczących sprawiedliwości bez modyfikowania samych modeli.
Na przykład można zastosować przetwarzanie końcowe w przypadku modelu klasyfikacji binarnej, ustawiając próg klasyfikacji w taki sposób, aby równość szans była zachowana w przypadku danego atrybutu. W tym celu należy sprawdzić, czy odsetek prawdziwie pozytywnych wyników jest taki sam dla wszystkich wartości tego atrybutu.
dotrenowany model
Ogólne określenie, które zwykle odnosi się do wytrenowanego modelu, który przeszedł pewne przetwarzanie końcowe, np. co najmniej 1 z tych procesów:
PR AUC (obszar pod krzywą PR)
Obszar pod interpolowaną krzywą precyzji i czułości, uzyskany przez wykreślenie punktów (czułość, precyzja) dla różnych wartości progu klasyfikacji.
Praxis
Podstawowa biblioteka ML o wysokiej wydajności Pax. Praxis jest często nazywany „biblioteką warstw”.
Biblioteka Praxis zawiera nie tylko definicje klasy Layer, ale też większość jej komponentów pomocniczych, w tym:
- dane wejściowe,
- biblioteki konfiguracji (HParam i Fiddle);
- optymalizatory
Praxis zawiera definicje klasy Model.
precyzja
Miara dla modeli klasyfikacji, która odpowiada na to pytanie:
Gdy model przewidział klasę pozytywną, jaki odsetek prognoz był prawidłowy?
Oto wzór:
gdzie:
- Prawdziwie pozytywny wynik oznacza, że model prawidłowo przewidział klasę pozytywną.
- Wynik fałszywie pozytywny oznacza, że model błędnie przewidział klasę pozytywną.
Załóżmy na przykład, że model wygenerował 200 prognoz pozytywnych. Z tych 200 pozytywnych prognoz:
- 150 z nich to wyniki prawdziwie pozytywne.
- 50 z nich to wyniki fałszywie pozytywne.
W tym przypadku:
Porównaj z dokładnością i czułością.
Więcej informacji znajdziesz w sekcji Klasyfikacja: dokładność, czułość, precyzja i powiązane dane w kursie Machine Learning Crash Course.
precyzja przy k (precision@k)
Rodzaj danych do oceny uporządkowanej listy elementów. Precyzja przy k określa ułamek pierwszych k elementów na liście, które są „trafne”. Czyli:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
Wartość parametru k musi być mniejsza lub równa długości zwróconej listy. Pamiętaj, że długość zwróconej listy nie jest uwzględniana w obliczeniach.
Trafność jest często subiektywna. Nawet ludzie oceniający jakość często nie zgadzają się co do tego, które elementy są trafne.
Porównaj z:
krzywej precyzji i czułości
Krzywa precyzji w porównaniu z czułością przy różnych progach klasyfikacji.
prognoza
Dane wyjściowe modelu. Na przykład:
- Prognoza modelu klasyfikacji binarnej to klasa pozytywna lub negatywna.
- Prognoza modelu klasyfikacji wieloklasowej to jedna klasa.
- Prognoza modelu regresji liniowej to liczba.
błąd prognozy,
Wartość wskazująca, jak bardzo średnia prognoz różni się od średniej etykiet w zbiorze danych.
Nie należy go mylić z wyrazem obciążającym w modelach uczenia maszynowego ani z uprzedzeniami w kontekście etyki i uczciwości.
predykcyjne uczenie maszynowe,
Dowolny standardowy („klasyczny”) system uczenia maszynowego.
Termin predykcyjne uczenie maszynowe nie ma formalnej definicji. Termin ten odróżnia kategorię systemów ML, które nie są oparte na generatywnej AI.
równość prognoz
Wskaźnik obiektywności, który sprawdza, czy w przypadku danego modelu klasyfikacji wartości precyzji są równoważne w przypadku rozpatrywanych podgrup.
Na przykład model, który przewiduje przyjęcie do college'u, spełniałby warunek równości predykcyjnej w przypadku narodowości, gdyby jego wskaźnik precyzji był taki sam w przypadku Liliputów i Brobdingnagów.
Równość cen prognozowanych jest czasami nazywana równością cen prognozowanych.
Więcej informacji o równości predykcyjnej znajdziesz w sekcji 3.2.1 artykułu „Wyjaśnienie definicji sprawiedliwości”.
prognozowana równość cen
Inna nazwa równości predykcyjnej.
przetwarzanie wstępne,
przetwarzanie danych przed użyciem ich do trenowania modelu; Wstępne przetwarzanie może być tak proste, jak usunięcie z korpusu tekstów w języku angielskim słów, które nie występują w słowniku angielskim, lub tak złożone, jak przekształcenie punktów danych w taki sposób, aby wyeliminować jak najwięcej atrybutów skorelowanych z atrybutami związanymi z informacjami o charakterze poufnym. Przetwarzanie wstępne może pomóc w spełnieniu ograniczeń obiektywności.wytrenowany model,
Chociaż to pojęcie może odnosić się do dowolnego wytrenowanego modelu lub wytrenowanego wektora osadzania, obecnie termin „wytrenowany model” zwykle odnosi się do wytrenowanego dużego modelu językowego lub innej formy wytrenowanego modelu generatywnej AI.
Zobacz też model podstawowy i model podstawowy.
trening wstępny,
Początkowe trenowanie modelu na dużym zbiorze danych. Niektóre wstępnie wytrenowane modele są nieporadnymi gigantami i zwykle wymagają dopracowania w ramach dodatkowego trenowania. Na przykład eksperci w dziedzinie uczenia maszynowego mogą wstępnie wytrenować duży model językowy na podstawie obszernego zbioru danych tekstowych, np. wszystkich stron Wikipedii w języku angielskim. Po wstępnym trenowaniu model można jeszcze ulepszyć za pomocą jednej z tych technik:
- destylacja
- dostrajanie,
- dostrajanie przy użyciu instrukcji,
- dostrajanie konkretnych parametrów
- prompt-tuning
przekonanie a priori
Twoje przekonania na temat danych przed rozpoczęciem trenowania na nich modelu. Na przykład regularyzacja L2 opiera się na wcześniejszym przekonaniu, że wagi powinny być małe i zwykle rozłożone wokół zera.
Pro
Model Gemini z mniejszą liczbą parametrów niż Ultra, ale większą niż Nano. Więcej informacji znajdziesz w sekcji Gemini Pro.
probabilistyczny model regresji,
Model regresji, który wykorzystuje nie tylko wagi poszczególnych cech, ale też niepewność tych wag. Probabilistyczny model regresji generuje prognozę i jej niepewność. Na przykład probabilistyczny model regresji może dać prognozę 325 z odchyleniem standardowym 12. Więcej informacji o probabilistycznych modelach regresji znajdziesz w tym Colab na tensorflow.org.
funkcja gęstości prawdopodobieństwa
Funkcja, która określa częstotliwość występowania próbek danych o dokładnie określonej wartości. Gdy wartości zbioru danych są ciągłymi liczbami zmiennoprzecinkowymi, dokładne dopasowania występują rzadko. Jednak całkowanie funkcji gęstości prawdopodobieństwa od wartości x do wartości y daje oczekiwaną częstotliwość próbek danych między x a y.
Rozważmy na przykład rozkład normalny o średniej 200 i odchyleniu standardowym 30. Aby określić oczekiwaną częstotliwość próbek danych mieszczących się w zakresie od 211,4 do 218,7, możesz scałkować funkcję gęstości prawdopodobieństwa rozkładu normalnego w zakresie od 211,4 do 218,7.
prompt
Tekst wprowadzany jako dane wejściowe do dużego modelu językowego w celu warunkowania modelu, aby zachowywał się w określony sposób. Prompty mogą być krótkie, np. fraza, lub dowolnie długie (np. cały tekst powieści). Prompty należą do różnych kategorii, w tym do tych, które przedstawia poniższa tabela:
| Kategoria prompta | Przykład | Uwagi |
|---|---|---|
| Pytanie | Jak szybko może lecieć gołąb? | |
| Instrukcja | Napisz zabawny wiersz o arbitrażu. | Prompt, w którym prosisz duży model językowy o wykonanie jakiegoś działania. |
| Przykład | Przetłumacz kod Markdown na HTML. Przykład:
Markdown: * element listy HTML: <ul> <li>element listy</li> </ul> |
Pierwsze zdanie w tym przykładowym prompcie to instrukcja. Pozostała część promptu to przykład. |
| Rola | Wyjaśnij, dlaczego w uczeniu maszynowym stosuje się metodę spadku gradientowego. | Pierwsza część zdania to instrukcja, a wyrażenie „to a PhD in Physics” to część dotycząca roli. |
| Częściowe dane wejściowe, które model ma uzupełnić. | Premier Wielkiej Brytanii mieszka w | Częściowy prompt wejściowy może się nagle kończyć (jak w tym przykładzie) lub kończyć się podkreśleniem. |
Model generatywnej AI może odpowiadać na prompty za pomocą tekstu, kodu, obrazów, wektorów dystrybucyjnych, filmów… prawie wszystkiego.
uczenie oparte na promptach,
Funkcja niektórych modeli, która umożliwia im dostosowywanie zachowania w odpowiedzi na dowolne dane wejściowe w postaci tekstu (prompty). W typowym paradygmacie uczenia opartego na promptach duży model językowy odpowiada na prompt, generując tekst. Załóżmy na przykład, że użytkownik wpisuje ten prompt:
Podsumuj trzecią zasadę dynamiki Newtona.
Model, który potrafi uczyć się na podstawie promptów, nie jest specjalnie trenowany pod kątem odpowiadania na poprzedni prompt. Model „zna” wiele faktów z zakresu fizyki, wiele ogólnych reguł językowych i wiele informacji o tym, co stanowi ogólnie przydatne odpowiedzi. Ta wiedza wystarczy, aby udzielić (miejmy nadzieję) przydatnej odpowiedzi. Dodatkowe opinie użytkowników („Ta odpowiedź była zbyt skomplikowana” lub „Co to jest reakcja?”) umożliwiają niektórym systemom uczenia się na podstawie promptów stopniowe zwiększanie przydatności odpowiedzi.
projektowanie promptów,
Synonim terminu tworzenie promptów.
tworzenie promptów,
Sztuka tworzenia promptów, które pozwalają uzyskać oczekiwane odpowiedzi od dużego modelu językowego. Ludzie przeprowadzają inżynierię promptów. Tworzenie dobrze skonstruowanych promptów jest niezbędne, aby uzyskać przydatne odpowiedzi od dużego modelu językowego. Inżynieria promptów zależy od wielu czynników, w tym:
- Zbiór danych używany do wstępnego trenowania i ewentualnego dostrajania dużego modelu językowego.
- Temperatura i inne parametry dekodowania, których model używa do generowania odpowiedzi.
Projektowanie promptów to synonim tworzenia promptów.
Więcej informacji o tworzeniu przydatnych promptów znajdziesz w artykule Wprowadzenie do projektowania promptów.
zestaw promptów,
Grupa promptów do oceny dużego modelu językowego. Na przykład poniższa ilustracja przedstawia zestaw promptów składający się z 3 promptów:
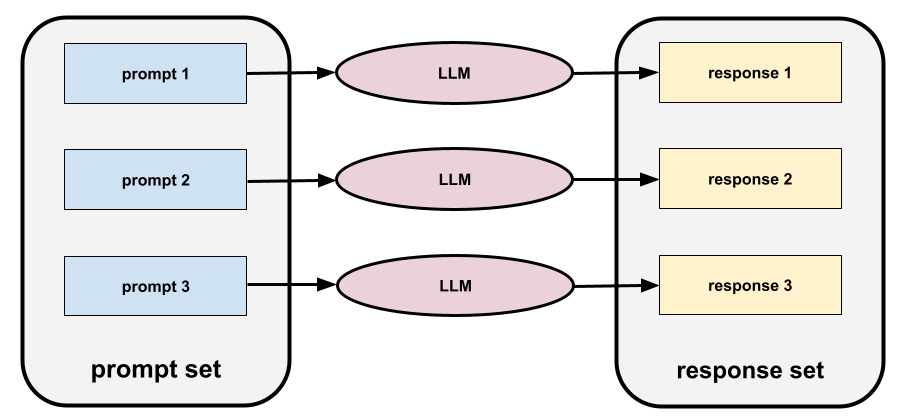
Dobre zestawy promptów składają się z wystarczająco „szerokiej” kolekcji promptów, aby dokładnie ocenić bezpieczeństwo i przydatność dużego modelu językowego.
Zobacz też zestaw odpowiedzi.
dostrajanie przy użyciu promptów,
Mechanizm wydajnego dostrajania parametrów, który uczy się „prefiksu” dodawanego przez system przed rzeczywistym promptem.
Jedną z odmian dostrajania promptów, czasami nazywaną dostrajaniem prefiksów, jest dodawanie prefiksu na każdej warstwie. W przeciwieństwie do tego większość metod dostrajania promptów dodaje tylko prefiks do warstwy wejściowej.
proxy (atrybuty wrażliwe)
Atrybut używany jako zamiennik atrybutu związanego z informacjami o charakterze poufnym. Na przykład kod pocztowy osoby może być używany jako przybliżone określenie jej dochodów, rasy lub pochodzenia etnicznego.etykiety proxy,
Dane używane do przybliżania etykiet, które nie są bezpośrednio dostępne w zbiorze danych.
Załóżmy na przykład, że musisz wytrenować model do prognozowania poziomu stresu pracowników. Twój zbiór danych zawiera wiele funkcji predykcyjnych, ale nie zawiera etykiety o nazwie stress level. Nie zrażasz się tym i wybierasz „wypadki w miejscu pracy” jako etykietę zastępczą dla poziomu stresu. W końcu pracownicy poddani silnemu stresowi częściej ulegają wypadkom niż ci, którzy są spokojni. A może jednak? Może się okazać, że wypadki w miejscu pracy wzrastają i maleją z różnych powodów.
Inny przykład: załóżmy, że chcesz, aby etykieta logiczna is it raining? (czy pada deszcz?) była częścią Twojego zbioru danych, ale nie zawiera on danych o deszczu. Jeśli dostępne są zdjęcia, możesz uznać zdjęcia osób z parasolami za etykietę zastępczą dla pytania czy pada deszcz? Czy to dobra etykieta zastępcza? Być może, ale w niektórych kulturach ludzie częściej noszą parasole, aby chronić się przed słońcem niż przed deszczem.
Etykiety zastępcze są często niedoskonałe. W miarę możliwości wybieraj rzeczywiste etykiety zamiast etykiet zastępczych. Jeśli jednak brakuje rzeczywistej etykiety, bardzo starannie wybierz etykietę zastępczą, wybierając najmniej szkodliwą z nich.
Więcej informacji znajdziesz w sekcji Zbiory danych: etykiety w szybkim szkoleniu z uczenia maszynowego.
funkcja czysta,
Funkcja, której dane wyjściowe zależą tylko od danych wejściowych i która nie ma efektów ubocznych. Funkcja czysta nie używa ani nie zmienia żadnego stanu globalnego, takiego jak zawartość pliku czy wartość zmiennej poza funkcją.
Funkcje czyste mogą służyć do tworzenia kodu bezpiecznego dla wątków, co jest korzystne w przypadku dzielenia kodu modelu na wiele chipów akceleratora.
Metody transformacji funkcji JAX wymagają, aby funkcje wejściowe były funkcjami czystymi.
Q
Funkcja Q
W uczeniu ze wzmocnieniem funkcja, która przewiduje oczekiwany zwrot z podjęcia działania w stanie, a następnie zastosowania danej strategii.
Funkcja Q jest też nazywana funkcją wartości stanu i działania.
Q-learning
W uczeniu ze wzmocnieniem algorytm umożliwia agentowi nauczenie się optymalnej funkcji Q procesu decyzyjnego Markowa przez zastosowanie równania Bellmana. Proces decyzyjny Markowa modeluje środowisko.
kwantyl
Każdy przedział w przedziałach kwantylowych.
skategoryzowanie w przedziałach kwantylowych
Rozdzielanie wartości cechy na zasobniki tak, aby każdy z nich zawierał taką samą (lub prawie taką samą) liczbę przykładów. Na przykład na poniższym rysunku 44 punkty są podzielone na 4 koszyki, z których każdy zawiera 11 punktów. Aby każdy zasobnik na wykresie zawierał tę samą liczbę punktów, niektóre zasobniki obejmują różne szerokości wartości x.

Więcej informacji znajdziesz w sekcji Dane liczbowe: dzielenie na przedziały w szybkim szkoleniu z uczenia maszynowego.
kwantyzacja,
Przeciążony termin, który może być używany w jeden z tych sposobów:
- Wdrażanie grupowania kwantylowego w przypadku konkretnej cechy.
- Przekształcanie danych w zera i jedynki w celu szybszego przechowywania, trenowania i wyciągania wniosków. Dane logiczne są bardziej odporne na szum i błędy niż inne formaty, więc kwantyzacja może poprawić poprawność modelu. Techniki kwantyzacji obejmują zaokrąglanie, obcinanie i grupowanie.
Zmniejszenie liczby bitów używanych do przechowywania parametrów modelu. Załóżmy na przykład, że parametry modelu są przechowywane jako 32-bitowe liczby zmiennoprzecinkowe. Kwantyzacja przekształca te parametry z 32-bitowych na 4-, 8- lub 16-bitowe. Kwantyzacja zmniejsza:
- Wykorzystanie zasobów obliczeniowych, pamięci, dysku i sieci
- Czas wnioskowania prognozy
- Zużycie energii
Kwantyzacja czasami zmniejsza jednak trafność prognoz modelu.
kolejka
Operacja TensorFlow, która implementuje strukturę danych kolejki. Zwykle używane w przypadku wejścia/wyjścia.
R
RAG
Skrót od generowania wspomaganego wyszukiwaniem.
las losowy,
Zespół drzew decyzyjnych, w którym każde drzewo decyzyjne jest trenowane z użyciem określonego losowego szumu, np. baggingu.
Lasy losowe to rodzaj lasu decyzyjnego.
Więcej informacji znajdziesz w sekcji Random Forest w kursie Decision Forests.
zasada losowa,
W uczeniu ze wzmocnieniem strategia, która losowo wybiera działanie.
pozycja (kolejność)
Pozycja porządkowa klasy w problematyce uczenia maszynowego, która kategoryzuje klasy od najwyższej do najniższej. Na przykład system rankingowy zachowań może uszeregować nagrody dla psa od najwyższej (stek) do najniższej (zwiędły jarmuż).
rank (Tensor)
Liczba wymiarów w Tensor. Na przykład skalar ma rangę 0, wektor – rangę 1, a macierz – rangę 2.
Nie należy mylić z pozycją (kolejnością).
ranking
Rodzaj uczenia nadzorowanego, którego celem jest uporządkowanie listy elementów.
oceniający,
Osoba, która przypisuje etykiety do przykładów. „Annotator” to inna nazwa oceniającego.
Więcej informacji znajdziesz w module Dane kategorialne: typowe problemy w kursie Machine Learning Crash Course.
wycofanie
Miara dla modeli klasyfikacji, która odpowiada na to pytanie:
Gdy dane podstawowe należały do klasy pozytywnej, jaki odsetek prognoz został przez model prawidłowo zaklasyfikowany jako klasa pozytywna?
Oto wzór:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
gdzie:
- Prawdziwie pozytywny wynik oznacza, że model prawidłowo przewidział klasę pozytywną.
- Fałszywie negatywny wynik oznacza, że model błędnie przewidział klasę negatywną.
Załóżmy na przykład, że model dokonał 200 prognoz na podstawie przykładów, w których prawdziwa klasa to klasa pozytywna. Z tych 200 prognoz:
- 180 z nich to wyniki prawdziwie pozytywne.
- 20 z nich to wyniki fałszywie negatywne.
W tym przypadku:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
Więcej informacji znajdziesz w artykule Klasyfikacja: dokładność, czułość, precyzja i powiązane dane.
czułość przy k (recall@k)
Miara oceny systemów, które generują uporządkowaną listę elementów. Wartość k w przypadku miary Recall określa odsetek trafnych elementów w pierwszych k elementach na liście w stosunku do łącznej liczby zwróconych trafnych elementów.
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
Kontrast z precyzją przy k.
system rekomendacji,
System, który wybiera dla każdego użytkownika stosunkowo mały zestaw pożądanych elementów z dużego korpusu. Na przykład system rekomendacji filmów może polecić 2 filmy z korpusu 100 tys. filmów, wybierając Casablancę i Filadelfijską opowieść dla jednego użytkownika oraz Wonder Woman i Czarną Panterę dla innego. System rekomendacji filmów może opierać swoje rekomendacje na takich czynnikach jak:
- filmy, które ocenili lub obejrzeli podobni użytkownicy;
- gatunek, reżyserzy, aktorzy, docelowa grupa demograficzna…
Więcej informacji znajdziesz w kursie dotyczącym systemów rekomendacji.
Jednostka liniowa z progowaniem (ReLU)
Funkcja aktywacji o tym działaniu:
- Jeśli dane wejściowe są ujemne lub równe zero, dane wyjściowe wynoszą 0.
- Jeśli dane wejściowe są dodatnie, dane wyjściowe są równe danym wejściowym.
Na przykład:
- Jeśli dane wejściowe to -3, dane wyjściowe to 0.
- Jeśli dane wejściowe to +3, dane wyjściowe to 3,0.
Oto wykres funkcji ReLU:
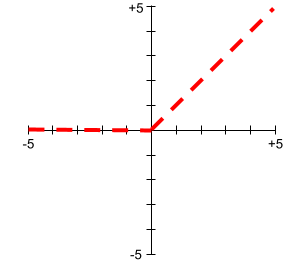
ReLU to bardzo popularna funkcja aktywacji. Pomimo prostego działania funkcja ReLU umożliwia sieci neuronowej uczenie się nieliniowych zależności między cechami a etykietą.
rekurencyjna sieć neuronowa
Sieć neuronowa, która jest celowo uruchamiana wielokrotnie, a części każdego uruchomienia są wykorzystywane w kolejnym uruchomieniu. W szczególności warstwy ukryte z poprzedniego uruchomienia stanowią część danych wejściowych dla tej samej warstwy ukrytej w następnym uruchomieniu. Rekurencyjne sieci neuronowe są szczególnie przydatne do oceny sekwencji, dzięki czemu warstwy ukryte mogą uczyć się na podstawie poprzednich przebiegów sieci neuronowej na wcześniejszych częściach sekwencji.
Na przykład na poniższym rysunku widać rekurencyjną sieć neuronową, która jest uruchamiana 4 razy. Zwróć uwagę, że wartości wyuczone w warstwach ukrytych podczas pierwszego przebiegu stają się częścią danych wejściowych tych samych warstw ukrytych podczas drugiego przebiegu. Podobnie wartości wyuczone w warstwie ukrytej w drugim przebiegu stają się częścią danych wejściowych tej samej warstwy ukrytej w trzecim przebiegu. W ten sposób rekurencyjna sieć neuronowa stopniowo uczy się i przewiduje znaczenie całego ciągu, a nie tylko poszczególnych słów.

tekst referencyjny,
Odpowiedź eksperta na prompt. Na przykład w przypadku tego prompta:
Przetłumacz pytanie „What is your name?” z angielskiego na francuski.
Odpowiedź eksperta może wyglądać tak:
Comment vous appelez-vous?
Różne wskaźniki (np. ROUGE) mierzą stopień, w jakim tekst referencyjny pasuje do wygenerowanego tekstu modelu ML.
model regresji,
Nieformalnie: model, który generuje prognozę liczbową. (Dla porównania model klasyfikacji generuje prognozę klasy). Na przykład wszystkie te modele to modele regresji:
- Model, który prognozuje wartość określonego domu w euro,np. 423 000.
- Model, który prognozuje średnią długość życia danego drzewa w latach, np.23,2.
- Model, który prognozuje ilość deszczu w calach, jaka spadnie w danym mieście w ciągu najbliższych 6 godzin, np.0,18.
Dwa popularne rodzaje modeli regresji to:
- Regresja liniowa, która znajduje linię najlepiej dopasowującą wartości etykiet do cech.
- Regresja logistyczna, która generuje prawdopodobieństwo z przedziału od 0,0 do 1,0, które system zwykle mapuje na prognozę klasy.
Nie każdy model, który generuje prognozy liczbowe, jest modelem regresji. W niektórych przypadkach prognoza numeryczna jest w rzeczywistości modelem klasyfikacji, który ma numeryczne nazwy klas. Na przykład model, który prognozuje numeryczny kod pocztowy, jest modelem klasyfikacji, a nie modelem regresji.
regularyzacja
Każdy mechanizm, który zmniejsza nadmierne dopasowanie. Popularne typy regularyzacji to:
- Regularyzacja L1
- Regularyzacja L2
- regularyzacja przez wyłączanie,
- wczesne zatrzymanie (nie jest to formalna metoda regularyzacji, ale może skutecznie ograniczać przetrenowanie);
Regularyzację można też zdefiniować jako karę za złożoność modelu.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: złożoność modelu w kursie Machine Learning Crash Course.
współczynnik regularyzacji
Liczba określająca względne znaczenie regularyzacji podczas trenowania. Zwiększenie współczynnika regularyzacji zmniejsza nadmierne dopasowanie, ale może zmniejszyć moc predykcyjną modelu. Z kolei zmniejszenie lub pominięcie współczynnika regularyzacji zwiększa przetrenowanie.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: regularyzacja L2 w szybkim szkoleniu z uczenia maszynowego.
uczenie się przez wzmacnianie (RL),
Rodzina algorytmów, które uczą się optymalnej strategii, której celem jest zmaksymalizowanie zwrotu podczas interakcji z otoczeniem. Na przykład ostateczną nagrodą w większości gier jest zwycięstwo. Systemy uczenia ze wzmocnieniem mogą stać się ekspertami w graniu w złożone gry, oceniając sekwencje poprzednich ruchów, które ostatecznie doprowadziły do zwycięstwa, oraz sekwencje, które ostatecznie doprowadziły do porażki.
Uczenie się przez wzmacnianie na podstawie opinii użytkowników (RLHF)
Wykorzystywanie opinii osób oceniających do poprawy jakości odpowiedzi modelu. Na przykład mechanizm RLHF może poprosić użytkowników o ocenę jakości odpowiedzi modelu za pomocą emotikonu 👍 lub 👎. System może następnie dostosowywać przyszłe odpowiedzi na podstawie tych opinii.
ReLU
Skrót od Rectified Linear Unit.
bufor powtórki
W algorytmach podobnych do DQN pamięć używana przez agenta do przechowywania przejść między stanami na potrzeby powtórki doświadczeń.
replika
Kopia (lub część) zbioru treningowego lub modelu, zwykle przechowywana na innym urządzeniu. Na przykład system może używać tej strategii do wdrażania równoległości danych:
- Umieść repliki istniejącego modelu na wielu maszynach.
- Wysyłaj do każdej repliki różne podzbiory zbioru treningowego.
- Zagreguj aktualizacje parametru.
Replika może też odnosić się do innej kopii serwera wnioskowania. Zwiększenie liczby replik zwiększa liczbę żądań, które system może obsługiwać jednocześnie, ale także zwiększa koszty obsługi.
błąd raportowania,
Fakt, że częstotliwość, z jaką ludzie piszą o działaniach, wynikach lub właściwościach, nie odzwierciedla ich rzeczywistej częstotliwości występowania ani stopnia, w jakim dana właściwość jest charakterystyczna dla klasy osób. Błąd raportowania może wpływać na skład danych, na podstawie których uczą się systemy uczenia maszynowego.
Na przykład w książkach słowo śmiał się występuje częściej niż oddychał. Model uczenia maszynowego, który szacuje względną częstotliwość śmiechu i oddechu na podstawie korpusu książek, prawdopodobnie uzna, że śmiech występuje częściej niż oddech.
Więcej informacji znajdziesz w module Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
reprezentacja,
Proces mapowania danych na przydatne funkcje.
ponowne ustalanie rankingu,
Ostatni etap systemu rekomendacji, podczas którego ocenione elementy mogą być ponownie oceniane według innego algorytmu (zwykle nieopartego na uczeniu maszynowym). Ponowne rankingowanie ocenia listę elementów wygenerowaną w fazie oceny, podejmując działania takie jak:
- eliminowanie produktów, które użytkownik już kupił;
- zwiększanie wyniku nowszych elementów;
Więcej informacji znajdziesz w sekcji Ponowne rankingowanie w kursie Systemy rekomendacji.
odpowiedź
Tekst, obrazy, dźwięki lub filmy, które generatywny model AI wywnioskuje. Innymi słowy, prompt to dane wejściowe dla modelu generatywnej AI, a odpowiedź to dane wyjściowe.
zbiór odpowiedzi,
Zbiór odpowiedzi dużego modelu językowego jest zwracany do zestawu promptów wejściowych.
generowanie wspomagane wyszukiwaniem
Technika poprawiająca jakość danych wyjściowych dużego modelu językowego (LLM) poprzez powiązanie ich ze źródłami wiedzy pobranymi po wytrenowaniu modelu. RAG zwiększa dokładność odpowiedzi LLM, zapewniając wytrenowanemu modelowi LLM dostęp do informacji pobranych z zaufanych baz wiedzy lub dokumentów.
Najczęstsze powody korzystania z generowania z wyszukiwaniem to:
- Zwiększanie dokładności generowanych przez model odpowiedzi.
- Udostępnianie modelowi wiedzy, na której nie został wytrenowany.
- zmieniać wiedzę, z której korzysta model;
- umożliwiać modelowi cytowanie źródeł;
Załóżmy na przykład, że aplikacja do chemii korzysta z interfejsu PaLM API do generowania podsumowań związanych z zapytaniami użytkowników. Gdy backend aplikacji otrzyma zapytanie:
- Wyszukuje („pobiera”) dane pasujące do zapytania użytkownika.
- Dołącza („wzbogaca”) odpowiednie dane chemiczne do zapytania użytkownika.
- Instruuje model LLM, aby utworzył podsumowanie na podstawie dołączonych danych.
powrót
W uczeniu ze wzmocnieniem, przy danej strategii i danym stanie, zwrot to suma wszystkich nagród, które agent spodziewa się otrzymać, postępując zgodnie z strategią od stanu do końca epizodu. Agent uwzględnia opóźniony charakter oczekiwanych nagród, dyskontując je zgodnie z przejściami stanu wymaganymi do ich uzyskania.
Jeśli więc współczynnik rabatu wynosi \(\gamma\), a \(r_0, \ldots, r_{N}\)oznacza nagrody do końca odcinka, obliczenie zwrotu wygląda następująco:
nagrody
W uczeniu przez wzmacnianie jest to wynik liczbowy podjęcia działania w stanie, określony przez środowisko.
regularyzacja grzbietowa
Synonim regularyzacji L2. Termin regularyzacja grzbietowa jest częściej używany w kontekście czystej statystyki, a termin regularyzacja L2 jest częściej używany w uczeniu maszynowym.
RNN
Skrót od rekurencyjnych sieci neuronowych.
Krzywa charakterystyki operacyjnej odbiornika (ROC)
Wykres przedstawiający odsetek prawdziwie pozytywnych wyników w porównaniu z odsetkiem fałszywie pozytywnych wyników dla różnych progów klasyfikacji w klasyfikacji binarnej.
Kształt krzywej ROC wskazuje na zdolność modelu klasyfikacji binarnej do oddzielania klas pozytywnych od negatywnych. Załóżmy na przykład, że binarny model klasyfikacji doskonale oddziela wszystkie klasy negatywne od wszystkich klas pozytywnych:
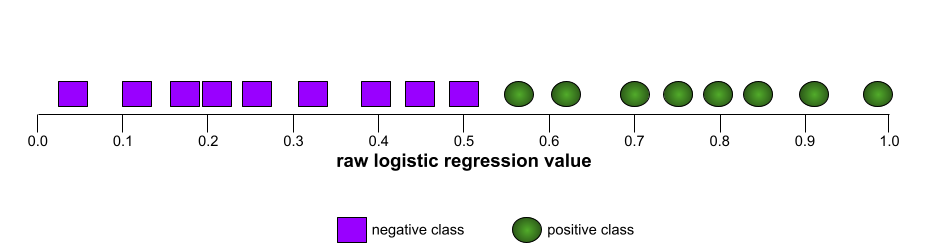
Krzywa ROC poprzedniego modelu wygląda tak:
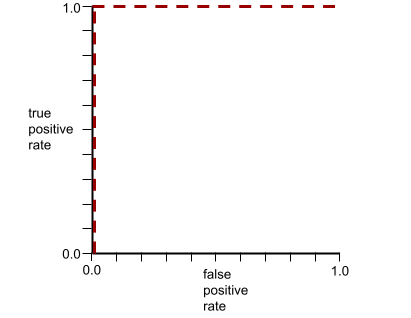
Z kolei na poniższej ilustracji przedstawiono surowe wartości regresji logistycznej w przypadku bardzo słabego modelu, który w ogóle nie potrafi odróżnić klas negatywnych od pozytywnych:
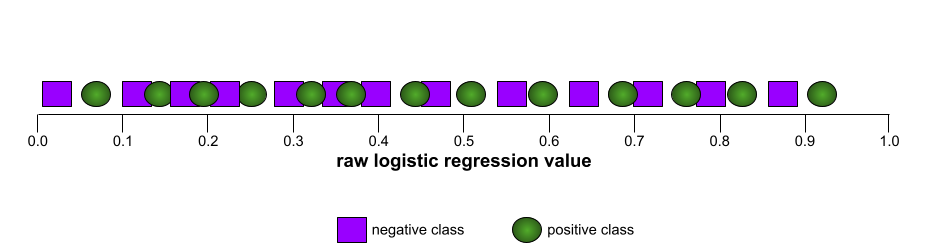
Krzywa ROC tego modelu wygląda tak:
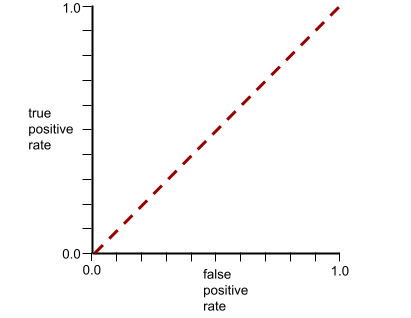
Tymczasem w rzeczywistości większość modeli klasyfikacji binarnej w pewnym stopniu rozdziela klasy pozytywne i negatywne, ale zwykle nie robi tego idealnie. Typowa krzywa ROC znajduje się więc gdzieś pomiędzy tymi dwoma skrajnościami:
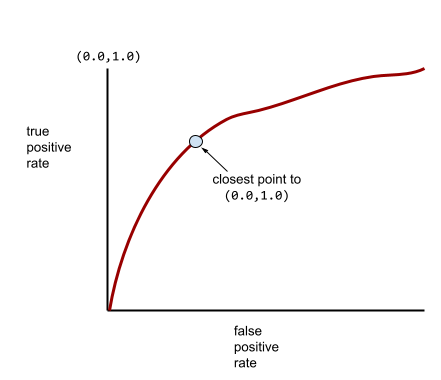
Punkt na krzywej ROC najbliższy punktowi (0,0, 1,0) teoretycznie określa idealny próg klasyfikacji. Na wybór idealnego progu klasyfikacji wpływa jednak kilka innych problemów z rzeczywistego świata. Na przykład fałszywe negatywy mogą powodować znacznie więcej problemów niż fałszywe pozytywy.
Wskaźnik liczbowy o nazwie AUC podsumowuje krzywą ROC w postaci pojedynczej wartości zmiennoprzecinkowej.
role prompting
Prompt, który zwykle zaczyna się od zaimka ty i mówi modelowi generatywnej AI, aby podczas generowania odpowiedzi udawał określoną osobę lub odgrywał określoną rolę. Prompt dotyczący roli może pomóc modelowi generatywnej AI w odpowiednim „nastawieniu”, aby wygenerować bardziej przydatną odpowiedź. W zależności od rodzaju odpowiedzi, jakiej oczekujesz, możesz na przykład użyć dowolnego z tych promptów dotyczących roli:
Masz tytuł doktora informatyki.
Jesteś inżynierem oprogramowania, który lubi cierpliwie tłumaczyć podstawy Pythona nowym studentom programowania.
Jesteś bohaterem kina akcji o bardzo specyficznych umiejętnościach programistycznych. Zapewnij mnie, że znajdziesz konkretny element na liście Pythona.
poziom główny
Węzeł początkowy (pierwszy warunek) w drzewie decyzyjnym. Zgodnie z konwencją korzeń umieszcza się u góry drzewa decyzyjnego. Na przykład:

katalog główny
Katalog, który określasz na potrzeby hostowania podkatalogów plików punktów kontrolnych i zdarzeń TensorFlow wielu modeli.
Średnia kwadratowa błędów (RMSE)
Pierwiastek kwadratowy z błędu średniokwadratowego.
niezmienniczość ze względu na obrót,
W przypadku problemu z klasyfikacją obrazów jest to zdolność algorytmu do prawidłowego klasyfikowania obrazów nawet wtedy, gdy zmienia się ich orientacja. Na przykład algorytm może rozpoznać rakietę tenisową, niezależnie od tego, czy jest skierowana w górę, w bok czy w dół. Pamiętaj, że niezmienność w przypadku obrotu nie zawsze jest pożądana. Na przykład odwrócona cyfra 9 nie powinna być klasyfikowana jako 9.
Zobacz też niezmienność translacyjną i niezmienność rozmiaru.
ROUGE (Recall-Oriented Understudy for Gisting Evaluation)
Rodzina wskaźników, które oceniają modele automatycznego podsumowywania i tłumaczenia maszynowego. Wskaźniki ROUGE określają stopień, w jakim tekst referencyjny pokrywa się z wygenerowanym tekstem modelu ML. Każdy element rodziny ROUGE mierzy nakładanie się w inny sposób. Wyższe wyniki ROUGE wskazują na większe podobieństwo między tekstem referencyjnym a wygenerowanym niż niższe wyniki ROUGE.
Każdy element rodziny ROUGE generuje zwykle te dane:
- Precyzja
- Czułość
- F1
Szczegółowe informacje i przykłady znajdziesz w tych artykułach:
ROUGE-L
Wskaźnik z rodziny ROUGE, który koncentruje się na długości najdłuższego wspólnego podciągu w tekście referencyjnym i tekście wygenerowanym. Wartości przywołania i precyzji dla ROUGE-L są obliczane według tych wzorów:
Następnie możesz użyć wskaźnika F1, aby połączyć czułość ROUGE-L i precyzję ROUGE-L w jeden wskaźnik:
ROUGE-L ignoruje znaki nowego wiersza w tekście referencyjnym i wygenerowanym, więc najdłuższy wspólny podciąg może obejmować wiele zdań. Jeśli tekst referencyjny i wygenerowany składają się z wielu zdań, lepszym wskaźnikiem jest zwykle odmiana ROUGE-L o nazwie ROUGE-Lsum. Wskaźnik ROUGE-Lsum określa najdłuższy wspólny podciąg dla każdego zdania w fragmencie, a następnie oblicza średnią tych najdłuższych wspólnych podciągów.
ROUGE-N
Zestaw wskaźników z rodziny ROUGE, który porównuje wspólne n-gramy o określonym rozmiarze w tekście referencyjnym i tekście wygenerowanym. Na przykład:
- ROUGE-1 mierzy liczbę wspólnych tokenów w tekście referencyjnym i wygenerowanym.
- ROUGE-2 mierzy liczbę wspólnych bigramów (2-gramów) w tekście referencyjnym i wygenerowanym.
- ROUGE-3 mierzy liczbę wspólnych trigramów (3-gramów) w tekście referencyjnym i wygenerowanym.
Aby obliczyć wartość ROUGE-N dla dowolnego elementu rodziny ROUGE-N, możesz użyć tych wzorów:
Następnie możesz użyć wskaźnika F1, aby połączyć czułość i precyzję ROUGE-N w jeden wskaźnik:
ROUGE-S
Łagodna forma ROUGE-N, która umożliwia dopasowywanie skip-gramów. Oznacza to, że ROUGE-N zlicza tylko n-gramy, które są dokładnie dopasowane, ale ROUGE-S zlicza też n-gramy oddzielone co najmniej jednym słowem. Na przykład:
- tekst referencyjny: Białe chmury
- wygenerowany tekst: Białe, kłębiące się chmury
Podczas obliczania ROUGE-N 2-gram White clouds nie pasuje do White billowing clouds. Jednak podczas obliczania ROUGE-S fraza White clouds pasuje do frazy White billowing clouds.
R-kwadrat
Rodzaj danych regresji wskazujący, w jakim stopniu zmienność etykiety wynika z pojedynczej cechy lub zestawu cech. Wartość R-kwadrat mieści się w zakresie od 0 do 1 i można ją interpretować w ten sposób:
- Wartość R-kwadrat równa 0 oznacza, że żadna część zmienności etykiety nie jest spowodowana zestawem cech.
- Wartość R-kwadrat równa 1 oznacza, że wszystkie zmiany etykiety są spowodowane zestawem funkcji.
- Wartość R-kwadrat w zakresie od 0 do 1 określa, w jakim stopniu wariancję etykiety można przewidzieć na podstawie konkretnej cechy lub zestawu cech. Na przykład wartość R-kwadrat równa 0,10 oznacza, że 10% wariancji etykiety wynika z zestawu cech, a wartość R-kwadrat równa 0,20 oznacza, że 20% wariancji etykiety wynika z zestawu cech itd.
Wartość R kwadrat to kwadrat współczynnika korelacji Pearsona między wartościami prognozowanymi przez model a danymi podstawowymi.
S
błąd próbkowania,
Zobacz błąd doboru.
próbkowanie ze zwracaniem,
Metoda wybierania elementów ze zbioru kandydatów, w której ten sam element może być wybierany wielokrotnie. Określenie „z powtórzeniami” oznacza, że po każdym wyborze wybrany element jest zwracany do puli kandydatów. Metoda odwrotna, czyli próbkowanie bez zwracania, oznacza, że element kandydujący może zostać wybrany tylko raz.
Rozważmy na przykład ten zbiór owoców:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Załóżmy, że system losowo wybiera fig jako pierwszy element.
Jeśli używasz próbkowania ze zwracaniem, system wybiera drugi element z tego zbioru:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Tak, to ten sam zestaw co wcześniej, więc system może ponownie wybrać fig.
Jeśli używasz próbkowania bez zwracania, po wybraniu próbki nie można jej ponownie wybrać. Jeśli na przykład system losowo wybierze fig jako pierwszą próbkę, nie może jej ponownie wybrać.fig Dlatego system wybiera drugą próbkę z tego (mniejszego) zbioru:
fruit = {kiwi, apple, pear, cherry, lime, mango}SavedModel
Zalecany format zapisywania i przywracania modeli TensorFlow. SavedModel to niezależny od języka format serializacji z możliwością odzyskiwania, który umożliwia systemom i narzędziom wyższego poziomu tworzenie, wykorzystywanie i przekształcanie modeli TensorFlow.
Szczegółowe informacje znajdziesz w sekcji Zapisywanie i przywracanie w Przewodniku programisty TensorFlow.
Ekonomiczna
Obiekt TensorFlow odpowiedzialny za zapisywanie punktów kontrolnych modelu.
wartość skalarna
Pojedyncza liczba lub pojedynczy ciąg znaków, który można przedstawić jako tensor o randze 0. Na przykład te wiersze kodu tworzą w TensorFlow po 1 skalarze:
breed = tf.Variable("poodle", tf.string)
temperature = tf.Variable(27, tf.int16)
precision = tf.Variable(0.982375101275, tf.float64)skalowanie
Każde przekształcenie lub technika matematyczna, która zmienia zakres etykiety lub wartości cechy albo obu tych elementów. Niektóre formy skalowania są bardzo przydatne w przypadku przekształceń takich jak normalizacja.
Typowe formy skalowania przydatne w uczeniu maszynowym to:
- skalowanie liniowe, które zwykle wykorzystuje kombinację odejmowania i dzielenia, aby zastąpić pierwotną wartość liczbą z zakresu od –1 do +1 lub od 0 do 1.
- skalowanie logarytmiczne, które zastępuje pierwotną wartość jej logarytmem.
- Normalizacja z-score, która zastępuje oryginalną wartość liczbą zmiennoprzecinkową reprezentującą liczbę odchyleń standardowych od średniej tej cechy.
scikit-learn
Popularna platforma open source do uczenia maszynowego. Zobacz scikit-learn.org.
ocena
Część systemu rekomendacji, która podaje wartość lub ranking każdego elementu wygenerowanego w fazie generowania kandydatów.
błąd doboru,
Błędy w wyciąganych z danych próbkowanych wnioskach spowodowane procesem selekcji, który generuje systematyczne różnice między próbkami zaobserwowanymi w danych a tymi, które nie zostały zaobserwowane. Wyróżniamy te formy błędu doboru:
- Błąd pokrycia: populacja reprezentowana w zbiorze danych nie odpowiada populacji, dla której model uczenia maszynowego dokonuje prognoz.
- Błąd próbkowania: dane nie są zbierane losowo z grupy docelowej.
- Błąd braku odpowiedzi (nazywany też błędem uczestnictwa): użytkownicy z określonych grup rezygnują z udziału w ankietach w różnym stopniu niż użytkownicy z innych grup.
Załóżmy na przykład, że tworzysz model uczenia maszynowego, który przewiduje, czy dana osoba będzie zadowolona z filmu. Aby zebrać dane treningowe, rozdajesz ankiety wszystkim osobom w pierwszym rzędzie w kinie, w którym wyświetlany jest film. Na pierwszy rzut oka może się to wydawać rozsądnym sposobem na zebranie zbioru danych, ale ta forma zbierania danych może wprowadzić następujące rodzaje błędu doboru:
- błąd pokrycia: próbkowanie z populacji, która zdecydowała się obejrzeć film, może sprawić, że prognozy modelu nie będą uogólnione na osoby, które nie wyraziły jeszcze takiego poziomu zainteresowania filmem;
- błąd próbkowania: zamiast losowo wybrać próbę z docelowej populacji (wszystkich osób w kinie), wybrano tylko osoby w pierwszym rzędzie. Możliwe, że osoby siedzące w pierwszym rzędzie były bardziej zainteresowane filmem niż osoby w innych rzędach.
- błąd braku odpowiedzi: osoby o wyrazistych poglądach częściej odpowiadają na ankiety opcjonalne niż osoby o poglądach umiarkowanych. Ankieta dotycząca filmu jest opcjonalna, więc odpowiedzi będą raczej tworzyć rozkład dwumodalny niż rozkład normalny (w kształcie dzwonu).
mechanizm uwagi (nazywany też warstwą uwagi)
Warstwa sieci neuronowej, która przekształca sekwencję wektorów dystrybucyjnych (np. wektorów dystrybucyjnych tokenów) w inną sekwencję wektorów dystrybucyjnych. Każdy wektor dystrybucyjny w sekwencji wyjściowej jest tworzony przez integrację informacji z elementów sekwencji wejściowej za pomocą mechanizmu uwagi.
Część self w terminie samouwaga oznacza, że sekwencja zwraca uwagę na samą siebie, a nie na jakiś inny kontekst. Mechanizm uwagi to jeden z głównych elementów składowych modeli Transformer. Wykorzystuje on terminologię związaną z wyszukiwaniem w słowniku, taką jak „zapytanie”, „klucz” i „wartość”.
Warstwa samouwagi zaczyna od sekwencji reprezentacji wejściowych, po jednej dla każdego słowa. Reprezentacja wejściowa słowa może być prostym osadzeniem. W przypadku każdego słowa w sekwencji wejściowej sieć ocenia trafność słowa w odniesieniu do każdego elementu w całej sekwencji słów. Wyniki trafności określają, w jakim stopniu ostateczna reprezentacja słowa uwzględnia reprezentacje innych słów.
Rozważmy na przykład to zdanie:
Zwierzę nie przeszło przez ulicę, ponieważ było zbyt zmęczone.
Ilustracja poniżej (pochodząca z artykułu Transformer: A Novel Neural Network Architecture for Language Understanding) przedstawia wzorzec uwagi warstwy samouwagi dla zaimka it. Ciemność każdej linii wskazuje, w jakim stopniu poszczególne słowa przyczyniają się do reprezentacji:
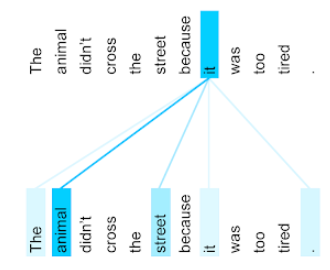
Warstwa samouważności wyróżnia słowa, które są istotne dla słowa „it”. W tym przypadku warstwa uwagi nauczyła się wyróżniać słowa, do których może się odnosić, przypisując najwyższą wagę słowu zwierzę.
W przypadku sekwencji n tokenów samouwaga przekształca sekwencję wektorów dystrybucyjnych n razy, po jednym razie na każdej pozycji w sekwencji.
Zobacz też uwagę i mechanizm wielogłowicowej uwagi.
uczenie samonadzorowane,
Rodzina technik przekształcania problemu uczenia nienadzorowanego w problem uczenia nadzorowanego przez tworzenie zastępczych etykiet na podstawie nieoznakowanych przykładów.
Niektóre modele oparte na transformerach, takie jak BERT, korzystają z uczenia bez nadzoru.
Uczenie z samodzielnym nadzorem to podejście uczenia częściowo nadzorowanego.
samodzielne szkolenie,
Odmiana uczenia bez nadzoru, która jest szczególnie przydatna, gdy spełnione są wszystkie te warunki:
- W zbiorze danych jest wysoki odsetek nieoznaczonych przykładów w porównaniu z oznaczonymi przykładami.
- Jest to problem klasyfikacji.
Samodzielne trenowanie polega na powtarzaniu tych 2 kroków, dopóki model nie przestanie się poprawiać:
- Użyj nadzorowanego uczenia maszynowego, aby wytrenować model na podstawie oznaczonych przykładów.
- Użyj modelu utworzonego w kroku 1, aby wygenerować prognozy (etykiety) dla nieoznaczonych przykładów. Przenieś te, w przypadku których masz dużą pewność, do oznaczonych przykładów z przewidywaną etykietą.
Zwróć uwagę, że w każdej iteracji kroku 2 dodawane są kolejne przykłady z etykietami, na podstawie których można trenować model w kroku 1.
uczenie częściowo nadzorowane,
Trenowanie modelu na danych, w których niektóre przykłady treningowe mają etykiety, a inne nie. Jedną z technik uczenia częściowo nadzorowanego jest wnioskowanie etykiet dla nieoznaczonych przykładów, a następnie trenowanie na podstawie wnioskowanych etykiet w celu utworzenia nowego modelu. Uczenie półnadzorowane może być przydatne, jeśli etykiety są drogie w uzyskaniu, ale przykłady bez etykiet są dostępne w dużej ilości.
Samouczenie to jedna z metod uczenia częściowo nadzorowanego.
atrybut wrażliwy
Atrybut człowieka, który może wymagać szczególnej rozwagi z przyczyn prawnych, etycznych, społecznych lub osobistych.analiza nastawienia
Używanie algorytmów statystycznych lub uczenia maszynowego do określania ogólnego nastawienia grupy – pozytywnego lub negatywnego – do usługi, produktu, organizacji lub tematu. Na przykład za pomocą rozumienia języka naturalnego algorytm może przeprowadzić analizę nastawienia na podstawie tekstowych opinii o kursie uniwersyteckim, aby określić, w jakim stopniu studenci ogólnie lubili lub nie lubili kursu.
Więcej informacji znajdziesz w przewodniku po klasyfikacji tekstu.
model sekwencyjny,
Model, którego dane wejściowe są od siebie zależne w kolejności. Na przykład przewidywanie kolejnego filmu, który zostanie obejrzany, na podstawie sekwencji wcześniej obejrzanych filmów.
zadanie typu sekwencja do sekwencji
Zadanie, które konwertuje wejściową sekwencję tokenów na wyjściową sekwencję tokenów. Na przykład 2 popularne rodzaje zadań typu sekwencja na sekwencję to:
- Tłumacze:
- Przykładowa sekwencja wejściowa: „I love you”.
- Przykładowa sekwencja wyjściowa: „Je t'aime”.
- Odpowiadanie na pytania:
- Przykładowa sekwencja danych wejściowych: „Czy potrzebuję samochodu w Nowym Jorku?”
- Przykładowa sekwencja odpowiedzi: „Nie. Zostaw samochód w domu”.
porcja
Proces udostępniania wytrenowanego modelu w celu generowania prognoz za pomocą wnioskowania online lub wnioskowania offline.
shape (Tensor)
Liczba elementów w każdym wymiarze tensora. Kształt jest reprezentowany jako lista liczb całkowitych. Na przykład ten dwuwymiarowy tensor ma kształt [3,4]:
[[5, 7, 6, 4], [2, 9, 4, 8], [3, 6, 5, 1]]
TensorFlow używa formatu wierszowego (w stylu C) do reprezentowania kolejności wymiarów, dlatego kształt w TensorFlow to [3,4], a nie [4,3]. Inaczej mówiąc, w dwuwymiarowym tensorze TensorFlow kształt to [liczba wierszy, liczba kolumn].
Statyczny kształt to kształt tensora, który jest znany w momencie kompilacji.
Dynamiczny kształt jest nieznany w momencie kompilacji, a więc zależy od danych w czasie działania. Ten tensor może być reprezentowany w TensorFlow za pomocą wymiaru zastępczego, np. [3, ?].
fragment
Logiczny podział zbioru treningowego lub modelu. Zwykle proces tworzenia fragmentów polega na podzieleniu przykładów lub parametrów na (zwykle) równe części. Każdy fragment jest następnie przypisywany do innego urządzenia.
Dzielenie modelu na fragmenty to równoległość modelu, a dzielenie danych na fragmenty to równoległość danych.
kurczenie się,
Hiperparametr w wzmocnieniu gradientowym, który kontroluje przetrenowanie. Kurczenie się w przypadku wzmocnienia gradientowego jest analogiczne do tempa uczenia się w metodzie gradientu prostego. Skurcz to liczba dziesiętna z zakresu od 0,0 do 1,0. Niższa wartość kurczenia zmniejsza przeuczenie bardziej niż wyższa.
ocena równoległa,
Porównywanie jakości 2 modeli na podstawie oceny ich odpowiedzi na ten sam prompt. Załóżmy na przykład, że różnym modelom podano ten sam prompt:
Utwórz obraz uroczego psa żonglującego 3 piłkami.
W ocenie porównawczej oceniający wybiera obraz, który jest „lepszy” (dokładniejszy, piękniejsze, Cuter?).
funkcja sigmoid
Funkcja matematyczna, która „ściska” wartość wejściową do ograniczonego zakresu, zwykle od 0 do 1 lub od -1 do +1. Oznacza to, że możesz przekazać do funkcji sigmoidalnej dowolną liczbę (2, milion, minus miliard itp.), a wynik nadal będzie mieścił się w określonym zakresie. Wykres funkcji aktywacji sigmoid wygląda tak:

Funkcja sigmoid ma kilka zastosowań w uczeniu maszynowym, m.in.:
- Przekształcanie surowych danych wyjściowych modelu regresji logistycznej lub regresji wielomianowej w prawdopodobieństwo.
- Pełni funkcję funkcji aktywacji w niektórych sieciach neuronowych.
miara podobieństwa,
W algorytmach klastrowania jest to miara używana do określania, jak podobne są do siebie 2 przykłady.
jeden program / wiele danych (SPMD),
Technika równoległości, w której te same obliczenia są wykonywane równolegle na różnych urządzeniach na różnych danych wejściowych. Celem SPMD jest szybsze uzyskiwanie wyników. Jest to najpopularniejszy styl programowania równoległego.
niezależność od rozmiaru,
W przypadku problemu z klasyfikacją obrazów jest to zdolność algorytmu do prawidłowego klasyfikowania obrazów nawet wtedy, gdy zmienia się ich rozmiar. Na przykład algorytm może nadal identyfikować kota, niezależnie od tego, czy zużywa 2 mln czy 200 tys. pikseli. Pamiętaj, że nawet najlepsze algorytmy klasyfikacji obrazów mają praktyczne ograniczenia dotyczące niezmienności rozmiaru. Na przykład algorytm (lub człowiek) prawdopodobnie nie zaklasyfikuje prawidłowo obrazu kota, który zajmuje tylko 20 pikseli.
Zobacz też niezmienność na przesunięcie i niezmienność na obrót.
Więcej informacji znajdziesz w kursie o klastrowaniu.
szkicowanie,
W nienadzorowanym uczeniu maszynowym, kategorii algorytmów, które przeprowadzają wstępną analizę podobieństwa na przykładach. Algorytmy szkicowania używają funkcji haszującej wrażliwej na lokalizację, aby identyfikować punkty, które mogą być podobne, a następnie grupować je w zasobnikach.
Szkicowanie zmniejsza moc obliczeniową potrzebną do obliczania podobieństwa w przypadku dużych zbiorów danych. Zamiast obliczać podobieństwo dla każdej pary przykładów w zbiorze danych, obliczamy je tylko dla każdej pary punktów w każdym koszyku.
skip-gram
n-gram, który może pomijać słowa z oryginalnego kontekstu, co oznacza, że N słów mogło nie być pierwotnie sąsiadujących. Dokładniej mówiąc, „k-skip-n-gram” to n-gram, w którym można pominąć maksymalnie k słów.
Na przykład w przypadku wyrażenia „the quick brown fox” (szybki brązowy lis) możliwe są te 2-gramy:
- „the quick”
- „szybki brązowy”
- „brązowy lis”
„1-skip-2-gram” to para słów, między którymi znajduje się co najwyżej 1 słowo. Dlatego „the quick brown fox” ma te 1-skip 2-gramy:
- „the brown”
- „szybki lis”
Poza tym wszystkie 2-gramy są również 1-skip-2-gramami, ponieważ można pominąć mniej niż jedno słowo.
Skip-gramy są przydatne do lepszego zrozumienia kontekstu słowa. W tym przykładzie słowo „fox” było bezpośrednio powiązane ze słowem „quick” w zbiorze 1-skip-2-gramów, ale nie w zbiorze 2-gramów.
Skip-gramy pomagają trenować modele osadzania słów.
funkcja softmax
Funkcja, która określa prawdopodobieństwa dla każdej możliwej klasy w modelu klasyfikacji wieloklasowej. Suma prawdopodobieństw wynosi dokładnie 1,0. Na przykład w tabeli poniżej pokazujemy, jak funkcja softmax rozdziela różne prawdopodobieństwa:
| Obraz jest… | Prawdopodobieństwo |
|---|---|
| pies | 0,85 |
| kot | 0,13 |
| koń | 0,02 |
Funkcja softmax jest też nazywana pełną funkcją softmax.
Porównaj z próbkowaniem kandydatów.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: klasyfikacja wieloklasowa w kursie Machine Learning Crash Course.
dostrajanie promptów miękkich
Technika dostrajania dużego modelu językowego do konkretnego zadania bez wymagającego dużych zasobów dostrajania. Zamiast ponownie trenować wszystkie wagi w modelu, dostrajanie miękkiego promptu automatycznie dostosowuje prompt, aby osiągnąć ten sam cel.
W przypadku prompta tekstowego dostrajanie prompta zwykle dodaje do niego dodatkowe osadzenia tokenów i używa propagacji wstecznej do optymalizacji danych wejściowych.
„Twardy” prompt zawiera rzeczywiste tokeny zamiast osadzeń tokenów.
rzadka cecha,
Cechy, których wartości są w większości zerowe lub puste. Na przykład cecha zawierająca jedną wartość 1 i milion wartości 0 jest rzadka. Z kolei gęsta cecha ma wartości, które w większości nie są zerowe ani puste.
W uczeniu maszynowym zaskakująco wiele cech to cechy rzadkie. Funkcje kategorialne są zwykle rzadkie. Na przykład spośród 300 możliwych gatunków drzew w lesie pojedynczy przykład może wskazywać tylko klon. Lub z milionów możliwych filmów w bibliotece filmów pojedynczy przykład może identyfikować tylko „Casablancę”.
W modelu cechy rzadkie są zwykle reprezentowane za pomocą kodowania 1 z n. Jeśli kodowanie 1 z n jest duże, możesz umieścić na nim warstwę wektora dystrybucyjnego, aby zwiększyć wydajność.
rozproszona reprezentacja,
Przechowywanie tylko pozycji elementów o wartościach różnych od zera w rzadkim wektorze cech.
Załóżmy na przykład, że cecha kategorialna o nazwie species identyfikuje 36
gatunków drzew w określonym lesie. Załóżmy też, że każdy przykład identyfikuje tylko jeden gatunek.
W każdym przykładzie możesz użyć wektora typu one-hot do reprezentowania gatunku drzewa.
Wektor typu one-hot zawierałby jedną wartość 1 (reprezentującą w tym przykładzie konkretny gatunek drzewa) i 35 wartości 0 (reprezentujących 35 gatunków drzew, które nie występują w tym przykładzie). Reprezentacja maple w kodowaniu 1-z-N może wyglądać tak:

Alternatywnie rzadka reprezentacja po prostu identyfikuje pozycję danego gatunku. Jeśli maple znajduje się na pozycji 24, rzadka reprezentacja maple będzie wyglądać tak:
24
Zwróć uwagę, że rzadka reprezentacja jest znacznie bardziej zwarta niż reprezentacja typu one-hot.
Więcej informacji znajdziesz w sekcji Praca z danymi kategorialnymi w kursie Machine Learning Crash Course.
wektor rzadki,
Wektor, którego wartości to w większości zera. Zobacz też rzadkie i rzadkość.
rozproszenie
Liczba elementów ustawionych na zero (lub null) w wektorze lub macierzy podzielona przez łączną liczbę wpisów w tym wektorze lub macierzy. Załóżmy na przykład, że masz macierz ze 100 elementami, w której 98 komórek zawiera zero. Obliczenie rzadkości wygląda następująco:
Rzadkość cech odnosi się do rzadkości wektora cech, a rzadkość modelu – do rzadkości wag modelu.
uśrednianie przestrzenne,
Zobacz pule.
kodowanie specyfikacyjne,
Proces pisania i utrzymywania pliku opisującego oprogramowanie, które ma zostać utworzone. Następnie możesz poprosić model generatywnej AI o utworzenie oprogramowania, które spełnia opis w pliku.
Wygenerowany automatycznie kod zwykle wymaga iteracji. W kodowaniu specyfikacyjnym iteracyjnie modyfikujesz plik opisu. W kodowaniu konwersacyjnym iteracje wykonujesz w polu prompta. W praktyce automatyczne generowanie kodu czasami obejmuje zarówno kodowanie specyfikacyjne, jak i konwersacyjne.
podziel
W drzewie decyzyjnym to inna nazwa warunku.
rozdzielacz,
Podczas trenowania drzewa decyzyjnego procedura (i algorytm) odpowiedzialna za znajdowanie najlepszego warunku w każdym węźle.
SPMD
Skrót od single program / multiple data (jeden program / wiele danych).
kwadratowa funkcja straty zawiasu
Kwadrat straty hinge. Kwadratowa funkcja straty z zawiasem surowiej karze wartości odstające niż zwykła funkcja straty z zawiasem.
strata kwadratowa,
Synonim utratyL2.
etapowe trenowanie,
Metoda trenowania modelu w sekwencji odrębnych etapów. Może to być przyspieszenie procesu trenowania lub uzyskanie lepszej jakości modelu.
Ilustracja przedstawiająca podejście progresywnego układania w stos:
- Etap 1 zawiera 3 warstwy ukryte, etap 2 – 6 warstw ukrytych, a etap 3 – 12 warstw ukrytych.
- Etap 2 rozpoczyna trenowanie z wagami wyuczonymi na 3 warstwach ukrytych na etapie 1. Etap 3 rozpoczyna trenowanie z wagami wyuczonymi w 6 warstwach ukrytych na etapie 2.
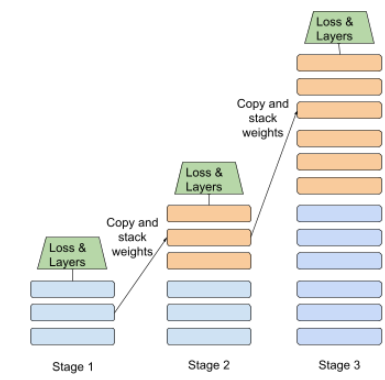
Zobacz też potokowanie.
stan
W uczeniu ze wzmocnieniem wartości parametrów opisujące bieżącą konfigurację środowiska, których agent używa do wyboru działania.
funkcja wartości stanu i działania
Synonim funkcji Q.
statyczne
Coś, co jest wykonywane jednorazowo, a nie w sposób ciągły. Terminy statyczny i offline są synonimami. Oto typowe zastosowania statycznych i offline w uczeniu maszynowym:
- Model statyczny (lub model offline) to model, który jest trenowany raz, a potem używany przez pewien czas.
- Trenowanie statyczne (lub trenowanie offline) to proces trenowania modelu statycznego.
- Wnioskowanie statyczne (lub wnioskowanie offline) to proces, w którym model generuje partię prognoz naraz.
Kontrast z dynamicznym.
wnioskowanie statyczne,
Synonim terminu wnioskowanie offline.
stacjonarność,
Cechy, których wartości nie zmieniają się w przypadku co najmniej jednego wymiaru, zwykle czasu. Na przykład cecha, której wartości w 2021 r. i 2023 r. są podobne, wykazuje stacjonarność.
W rzeczywistości bardzo niewiele cech wykazuje stacjonarność. Nawet cechy synonimiczne ze stabilnością (np. poziom morza) zmieniają się z czasem.
Porównaj z niestacjonarnością.
kroku
Przejście do przodu i do tyłu jednej partii.
Więcej informacji o przejściu w przód i w tył znajdziesz w artykule propagacja wsteczna.
wielkość kroku,
Synonim terminu tempo uczenia się.
stochastyczny spadek wzdłuż gradientu (SGD),
Algorytm spadku gradientowego, w którym rozmiar partii wynosi 1. Innymi słowy, SGD trenuje na jednym przykładzie wybranym losowo z zbioru treningowego.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
stride
W operacji splotu lub puli delta w każdym wymiarze następnej serii wycinków wejściowych. Na przykład poniższa animacja przedstawia krok (1,1) podczas operacji splotu. Dlatego następny wycinek wejściowy zaczyna się o 1 pozycję na prawo od poprzedniego wycinka wejściowego. Gdy operacja dotrze do prawej krawędzi, następny wycinek będzie przesunięty w lewo o jedną pozycję w dół.
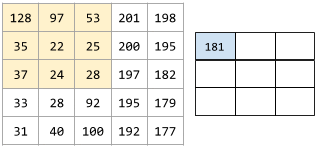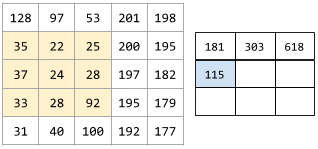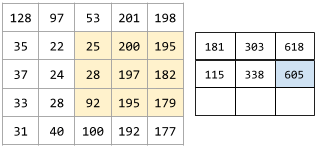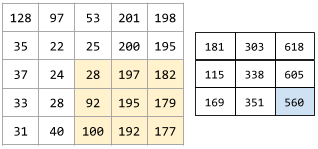
W powyższym przykładzie pokazano krok dwuwymiarowy. Jeśli macierz wejściowa jest trójwymiarowa, krok również będzie trójwymiarowy.
minimalizacja ryzyka strukturalnego (SRM),
Algorytm, który równoważy 2 cele:
- konieczność zbudowania modelu o największej mocy predykcyjnej (np. o najniższych stratach);
- Konieczność zachowania jak największej prostoty modelu (np. silna regularyzacja).
Na przykład funkcja, która minimalizuje utratę + regularyzację w zbiorze treningowym, jest algorytmem minimalizacji ryzyka strukturalnego.
Porównaj z minimalizacją ryzyka empirycznego.
podpróbkowanie,
Zobacz pule.
token podwyrazowy,
W modelach językowych token to podciąg słowa, który może być całym słowem.
Na przykład słowo „itemize” może zostać podzielone na części „item” (słowo podstawowe) i „ize” (przyrostek), z których każda jest reprezentowana przez osobny token. Podzielenie rzadkich słów na takie części, zwane podwyrazami, umożliwia modelom językowym działanie na bardziej popularnych częściach składowych słowa, takich jak przedrostki i przyrostki.
Z kolei popularne słowa, takie jak „going”, mogą nie być dzielone i mogą być reprezentowane przez jeden token.
podsumowanie
W TensorFlow wartość lub zbiór wartości obliczanych na określonym etapie, zwykle używanych do śledzenia danych modelu podczas trenowania.
nadzorowane uczenie maszynowe
Trenowanie modelu na podstawie cech i odpowiadających im etykiet. Uczenie nadzorowane jest podobne do uczenia się danego przedmiotu przez studiowanie zestawu pytań i odpowiedzi. Po opanowaniu mapowania pytań i odpowiedzi uczeń może udzielać odpowiedzi na nowe (nigdy wcześniej nie widziane) pytania dotyczące tego samego tematu.
Porównaj z nienadzorowanym uczeniem maszynowym.
Więcej informacji znajdziesz w sekcji dotyczącej uczenia nadzorowanego w kursie Wprowadzenie do uczenia maszynowego.
cecha syntetyczna,
Cechy, których nie ma wśród cech wejściowych, ale które są tworzone na podstawie co najmniej jednej z nich. Oto niektóre metody tworzenia cech syntetycznych:
- Podział cechy ciągłej na zasobniki zakresu.
- Tworzenie kombinacji cech.
- Mnożenie (lub dzielenie) jednej wartości cechy przez inne wartości cech lub przez samą siebie. Jeśli np.
aibsą cechami wejściowymi, to przykłady cech syntetycznych to:- ab
- a2
- Zastosowanie funkcji transcendentalnej do wartości cechy. Jeśli np.
cjest cechą wejściową, to przykłady cech syntetycznych to:- sin(c)
- ln(c)
Funkcje utworzone przez normalizację lub skalowanie nie są uznawane za funkcje syntetyczne.
T
T5
Model uczenia transferowego tekst – tekst wprowadzony przez Google AI w 2020 roku. T5 to model enkoder-dekoder oparty na architekturze Transformer, wytrenowany na bardzo dużym zbiorze danych. Sprawdza się w różnych zadaniach związanych z przetwarzaniem języka naturalnego, takich jak generowanie tekstu, tłumaczenie i odpowiadanie na pytania w formie konwersacji.
Nazwa T5 pochodzi od pięciu liter „T” w wyrażeniu „Text-to-Text Transfer Transformer”.
T5X
T5X
Platforma open source do uczenia maszynowego, która umożliwia tworzenie i trenowanie modeli przetwarzania języka naturalnego (NLP) na dużą skalę. T5 jest zaimplementowany w bazie kodu T5X (która jest oparta na JAX i Flax).
tabelaryczne uczenie Q
W uczeniu ze wzmocnieniem wdrażanie Q-learningu za pomocą tabeli do przechowywania funkcji Q dla każdej kombinacji stanu i działania.
cel
Synonim słowa etykieta.
sieć docelowa,
W głębokim uczeniu ze wzmocnieniem Q sieć neuronowa, która jest stabilną aproksymacją głównej sieci neuronowej, w której główna sieć neuronowa implementuje funkcję Q lub zasady. Następnie możesz wytrenować główną sieć na podstawie wartości Q przewidywanych przez sieć docelową. Zapobiega to pętli sprzężenia zwrotnego, która występuje, gdy główna sieć uczy się na podstawie wartości Q przewidywanych przez siebie. Unikanie tych opinii zwiększa stabilność trenowania.
działanie
Problem, który można rozwiązać za pomocą technik uczenia maszynowego, np.:
temperatura
Hiperparametr, który kontroluje stopień losowości danych wyjściowych modelu. Wyższe temperatury dają bardziej losowe wyniki, a niższe – mniej losowe.
Wybór najlepszej temperatury zależy od konkretnego zastosowania i wartości ciągu znaków.
dane czasowe,
Dane zarejestrowane w różnych momentach. Przykład: dane o sprzedaży płaszczy zimowych zapisywane każdego dnia roku to dane czasowe.
Tensor
Podstawowa struktura danych w programach TensorFlow. Tensory to N-wymiarowe (gdzie N może być bardzo duże) struktury danych, najczęściej skalary, wektory lub macierze. Elementy tensora mogą zawierać wartości całkowite, zmiennoprzecinkowe lub ciągi znaków.
TensorBoard
Panel, który wyświetla podsumowania zapisane podczas wykonywania co najmniej 1 programu TensorFlow.
TensorFlow
Platforma systemów uczących się na dużą skalę, rozproszona. Termin ten odnosi się też do podstawowej warstwy interfejsu API w stosie TensorFlow, która obsługuje ogólne obliczenia na wykresach przepływu danych.
TensorFlow jest używany głównie do uczenia maszynowego, ale możesz go też używać do zadań niezwiązanych z uczeniem maszynowym, które wymagają obliczeń numerycznych z użyciem wykresów przepływu danych.
TensorFlow Playground
Program, który wizualizuje, jak różne hiperparametry wpływają na trenowanie modelu (głównie sieci neuronowej). Otwórz stronę http://playground.tensorflow.org, aby wypróbować TensorFlow Playground.
TensorFlow Serving
Platforma do wdrażania wytrenowanych modeli w środowisku produkcyjnym.
Tensor Processing Unit (TPU)
Specjalizowany układ scalony (ASIC), który optymalizuje wydajność zadań uczenia maszynowego. Te układy ASIC są wdrażane jako wiele chipów TPU na urządzeniu TPU.
Ranga tensora
Zobacz rank (Tensor).
Kształt tensora
Liczba elementów, które Tensor zawiera w różnych wymiarach.
Na przykład [5, 10] tensor ma kształt 5 w jednym wymiarze i 10 w drugim.
Rozmiar tensora
Łączna liczba skalarów, które zawiera Tensor. Na przykład tensor [5, 10] ma rozmiar 50.
TensorStore
Biblioteka do efektywnego odczytywania i zapisywania dużych wielowymiarowych tablic.
warunek zakończenia,
W uczeniu ze wzmocnieniem warunki, które określają, kiedy kończy się epizod, np. gdy agent osiągnie określony stan lub przekroczy próg liczby przejść między stanami. Na przykład w kółku i krzyżyku (znanym też jako kółka i krzyżyki) epizod kończy się, gdy gracz zaznaczy 3 kolejne pola lub gdy wszystkie pola zostaną zaznaczone.
test
W drzewie decyzyjnym to inna nazwa warunku.
strata testowa
Wartość reprezentująca stratę modelu w odniesieniu do zbioru testowego. Podczas tworzenia modelu zwykle starasz się zminimalizować utratę testową. Dzieje się tak, ponieważ niski błąd testowy jest silniejszym sygnałem jakości niż niski błąd trenowania lub niski błąd walidacji.
Duża różnica między stratą na zbiorze testowym a stratą na zbiorze treningowym lub walidacyjnym może czasami sugerować, że należy zwiększyć współczynnik regularyzacji.
zbiór testowy
Podzbiór zbioru danych zarezerwowany do testowania wytrenowanego modelu.
Zwykle przykłady w zbiorze danych dzieli się na 3 odrębne podzbiory:
- zbiór treningowy,
- zbiór walidacyjny,
- zbiór testowy,
Każdy przykład w zbiorze danych powinien należeć tylko do jednego z powyższych podzbiorów. Na przykład jeden przykład nie powinien należeć zarówno do zbioru treningowego, jak i do zbioru testowego.
Zbiór treningowy i zbiór do weryfikacji są ściśle powiązane z trenowaniem modelu. Ponieważ zbiór testowy jest tylko pośrednio powiązany z trenowaniem, strata testowa jest mniej obciążonym i wyższej jakości wskaźnikiem niż strata trenowania lub strata weryfikacji.
Więcej informacji znajdziesz w sekcji Zbiory danych: dzielenie pierwotnego zbioru danych w szybkim szkoleniu z uczenia maszynowego.
zakres tekstu,
Zakres indeksu tablicy powiązany z określonym podsekcją ciągu tekstowego.
Na przykład słowo good w ciągu znaków w Pythonie s="Be good now" zajmuje zakres tekstu od 3 do 6.
tf.Example
Standardowy bufor protokołu do opisywania danych wejściowych na potrzeby trenowania lub wnioskowania modelu uczenia maszynowego.
tf.keras
Implementacja Keras zintegrowana z TensorFlow.
próg (w przypadku drzew decyzyjnych);
W warunku wyrównanym do osi wartość, z którą porównywana jest cecha. Na przykład w tym warunku wartością progową jest 75:
grade >= 75
Więcej informacji znajdziesz w dokładnym rozdzielaczu do klasyfikacji binarnej z cechami numerycznymi w kursie Decision Forests.
analiza szeregów czasowych,
Poddziedzina uczenia maszynowego i statystyki, która analizuje dane czasowe. Wiele rodzajów problemów związanych z uczeniem maszynowym wymaga analizy ciągów czasowych, w tym klasyfikacji, klastrowania, prognozowania i wykrywania anomalii. Możesz na przykład użyć analizy szeregów czasowych, aby na podstawie historycznych danych o sprzedaży prognozować przyszłą sprzedaż płaszczy zimowych w poszczególnych miesiącach.
krok czasowy
Jedna „rozwinięta” komórka w rekurencyjnej sieci neuronowej. Na przykład na poniższym rysunku przedstawiono 3 kroki czasowe (oznaczone indeksami dolnymi t-1, t i t+1):

token
W modelu językowym jest to najmniejsza jednostka, na podstawie której model się uczy i generuje prognozy. Token to zwykle jeden z tych elementów:
- słowo – na przykład wyrażenie „psy lubią koty” składa się z 3 tokenów słownych: „psy”, „lubią” i „koty”;
- znak – na przykład fraza „bike fish” składa się z 9 tokenów znakowych. (Pamiętaj, że pusta spacja jest liczona jako jeden token).
- podjednostki słowa – pojedyncze słowo może być pojedynczym lub wieloma tokenami; Słowo cząstkowe składa się z wyrazu podstawowego, przedrostka lub przyrostka. Na przykład model językowy, który używa subwordów jako tokenów, może traktować słowo „dogs” jako 2 tokeny (słowo „dog” i przyrostek liczby mnogiej „s”). Ten sam model językowy może traktować pojedyncze słowo „taller” jako 2 podjednostki (słowo podstawowe „tall” i przyrostek „er”).
W przypadku domen innych niż modele językowe tokeny mogą reprezentować inne rodzaje jednostek atomowych. Na przykład w przypadku widzenia komputerowego token może być podzbiorem obrazu.
Więcej informacji znajdziesz w sekcji Duże modele językowe w szybkim szkoleniu z uczenia maszynowego.
tokenizer
System lub algorytm, który tłumaczy sekwencję danych wejściowych na tokeny.
Większość nowoczesnych modeli podstawowych jest multimodalna. Tokenizator w systemie multimodalnym musi tłumaczyć każdy typ danych wejściowych na odpowiedni format. Na przykład w przypadku danych wejściowych składających się z tekstu i grafiki tokenizator może przetłumaczyć tekst wejściowy na podwyrazy, a obrazy wejściowe na małe fragmenty. Następnie tokenizator musi przekonwertować wszystkie tokeny na jedną ujednoliconą przestrzeń osadzania, co umożliwia modelowi „zrozumienie” strumienia danych wejściowych multimodalnych.
dokładność top-k,
Odsetek przypadków, w których „etykieta docelowa” pojawia się na pierwszych k pozycjach wygenerowanych list. Listy mogą zawierać spersonalizowane rekomendacje lub listę produktów uporządkowanych według funkcji softmax.
Dokładność top-k jest też nazywana dokładnością przy k.
wieża
Komponent głębokiej sieci neuronowej, który sam w sobie jest głęboką siecią neuronową. W niektórych przypadkach każda wieża odczytuje dane z niezależnego źródła danych i pozostaje niezależna, dopóki jej dane wyjściowe nie zostaną połączone w warstwie końcowej. W innych przypadkach (np. w enkoderze i dekoderze w wielu modelach Transformer) wieże są ze sobą połączone.
toksyczne
stopień, w jakim treści są obraźliwe, zawierają groźby lub są w inny sposób nieodpowiednie; Wiele modeli uczenia maszynowego potrafi identyfikować i mierzyć toksyczność. Większość tych modeli określa poziom toksyczności na podstawie wielu parametrów, takich jak poziom wulgaryzmów i poziom języka groźby.
TPU
Skrót od Tensor Processing Unit.
Układ TPU
Programowalny akcelerator algebry liniowej z pamięcią o wysokiej przepustowości na chipie, zoptymalizowany pod kątem zadań związanych z uczeniem maszynowym. Wiele układów TPU jest wdrażanych na urządzeniu TPU.
Urządzenie TPU
Płytka drukowana z wieloma układami TPU, interfejsami sieciowymi o wysokiej przepustowości i sprzętem do chłodzenia systemu.
Węzeł TPU
Zasób TPU w Google Cloud o określonym typie TPU. Węzeł TPU łączy się z siecią VPC z równorzędnej sieci VPC. Węzły TPU to zasób zdefiniowany w Cloud TPU API.
pod TPU
Określona konfiguracja urządzeń TPU w centrum danych Google. Wszystkie urządzenia w podzie TPU są połączone ze sobą za pomocą dedykowanej sieci o dużej szybkości. Pod TPU to największa konfiguracja urządzeń TPU dostępna w przypadku określonej wersji TPU.
Zasób TPU
Jednostka TPU w Google Cloud, którą tworzysz, zarządzasz lub z której korzystasz. Na przykład węzły TPU i typy TPU to zasoby TPU.
Wycinek TPU
Wycinek TPU to ułamek urządzeń TPU w podzie TPU. Wszystkie urządzenia w wycinku TPU są połączone ze sobą za pomocą dedykowanej sieci o dużej szybkości.
Typ TPU
Konfiguracja co najmniej 1 urządzenia TPU z konkretną wersją sprzętową TPU. Typ TPU wybierasz podczas tworzenia węzła TPU w Google Cloud. Na przykład v2-8
typ TPU to pojedyncze urządzenie TPU v2 z 8 rdzeniami. Typ TPU v3-2048 ma 256 połączonych w sieć urządzeń TPU v3 i łącznie 2048 rdzeni. Typy TPU to zasoby zdefiniowane w Cloud TPU API.
proces roboczy TPU
Proces, który działa na maszynie hosta i wykonuje programy uczenia maszynowego na urządzeniach TPU.
szkolenie
Proces określania optymalnych parametrów (wag i odchyleń) tworzących model. Podczas trenowania system odczytuje przykłady i stopniowo dostosowuje parametry. Podczas trenowania każdy przykład jest wykorzystywany od kilku do miliardów razy.
Więcej informacji znajdziesz w sekcji dotyczącej uczenia nadzorowanego w kursie Wprowadzenie do uczenia maszynowego.
strata podczas trenowania,
Wskaźnik reprezentujący stratę modelu podczas konkretnej iteracji trenowania. Załóżmy na przykład, że funkcja straty to średnia kwadratowa błędów. Załóżmy, że strata treningowa (średni błąd kwadratowy) w 10 iteracji wynosi 2,2, a w 100 iteracji – 1,9.
Krzywa straty przedstawia stratę podczas trenowania w zależności od liczby iteracji. Krzywa straty zawiera te wskazówki dotyczące trenowania:
- Spadek oznacza, że model się poprawia.
- Wznosząca się linia oznacza, że model się pogarsza.
- Płaska krzywa oznacza, że model osiągnął zbieżność.
Na przykład poniższa nieco wyidealizowana krzywa strat pokazuje:
- Strome nachylenie w dół w początkowych iteracjach, co oznacza szybką poprawę modelu.
- Stopniowo spłaszczająca się (ale nadal opadająca) krzywa aż do końca trenowania, co oznacza dalsze ulepszanie modelu w nieco wolniejszym tempie niż w początkowych iteracjach.
- Płaski spadek pod koniec trenowania, co sugeruje zbieżność.
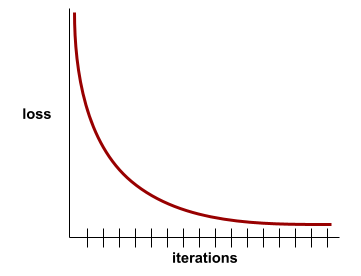
Utrata podczas trenowania jest ważna, ale zobacz też uogólnianie.
zniekształcenie między trenowaniem a zastosowaniem praktycznym
Różnica między wydajnością modelu podczas trenowania a wydajnością tego samego modelu podczas stosowania.
zbiór treningowy,
Podzbiór zbioru danych używany do trenowania modelu.
Przykłady w zbiorze danych są zwykle dzielone na 3 odrębne podzbiory:
- zbiór treningowy,
- zbiór walidacyjny,
- zbiór testowy,
Najlepiej, aby każdy przykład w zbiorze danych należał tylko do jednego z powyższych podzbiorów. Na przykład pojedynczy przykład nie powinien należeć zarówno do zbioru treningowego, jak i do zbioru do weryfikacji.
Więcej informacji znajdziesz w sekcji Zbiory danych: dzielenie pierwotnego zbioru danych w szybkim szkoleniu z uczenia maszynowego.
trajektoria
W uczeniu ze wzmocnieniem ciąg krotek reprezentujących ciąg przejść stanu agenta, gdzie każda krotka odpowiada stanowi, działaniu, nagrodzie i następnemu stanowi dla danego przejścia stanu.
uczenie transferowe,
Przenoszenie informacji z jednego zadania uczenia maszynowego do drugiego. Na przykład w uczeniu wielozadaniowym jeden model rozwiązuje wiele zadań, np. model głęboki, który ma różne węzły wyjściowe dla różnych zadań. Uczenie przez przenoszenie może polegać na przenoszeniu wiedzy z rozwiązania prostszego zadania do bardziej złożonego lub z zadania, w którym jest więcej danych, do zadania, w którym jest ich mniej.
Większość systemów uczenia maszynowego rozwiązuje jedno zadanie. Uczenie się przez transfer to pierwszy krok w kierunku sztucznej inteligencji, w którym jeden program może rozwiązywać wiele zadań.
Transformator
Architektura sieci neuronowej opracowana w Google, która wykorzystuje mechanizmy samodzielnego uczenia do przekształcania sekwencji osadzania wejściowego w sekwencję osadzania wyjściowego bez użycia splotów ani rekurencyjnych sieci neuronowych. Model Transformer można traktować jako stos warstw samouwagi.
Transformator może zawierać dowolny z tych elementów:
Koder przekształca sekwencję wektorów dystrybucyjnych w nową sekwencję o tej samej długości. Koder zawiera N identycznych warstw, z których każda składa się z 2 podwarstw. Te 2 podwarstwy są stosowane na każdej pozycji sekwencji wektorów dystrybucyjnych danych wejściowych, przekształcając każdy element sekwencji w nowy wektor dystrybucyjny. Pierwsza podwarstwa enkodera agreguje informacje z całej sekwencji wejściowej. Druga podwarstwa kodera przekształca zagregowane informacje w wektor wyjściowy.
Dekoder przekształca sekwencję wektorów wejściowych w sekwencję wektorów wyjściowych, która może mieć inną długość. Dekoder zawiera też N identycznych warstw z 3 podwarstwami, z których 2 są podobne do podwarstw kodera. Trzecia podwarstwa dekodera pobiera dane wyjściowe z enkodera i stosuje mechanizm samodzielnego uwagi, aby zbierać z nich informacje.
Wpis na blogu Transformer: A Novel Neural Network Architecture for Language Understanding (Transformer: nowatorska architektura sieci neuronowych na potrzeby rozumienia języka) zawiera dobre wprowadzenie do transformatorów.
Więcej informacji znajdziesz w artykule LLM: czym jest duży model językowy? w szybkim szkoleniu z systemów uczących się.
niezmienniczość na przesunięcie
W przypadku problemu z klasyfikacją obrazów jest to zdolność algorytmu do prawidłowego klasyfikowania obrazów nawet wtedy, gdy zmienia się położenie obiektów na obrazie. Na przykład algorytm może nadal rozpoznawać psa, niezależnie od tego, czy znajduje się on w centrum kadru, czy na jego lewym końcu.
Zobacz też niezależność od rozmiaru i niezależność od obrotu.
trigram
N-gram, w którym N=3.
wynik prawdziwie negatywny (TN),
Przykład, w którym model prawidłowo przewiduje klasę negatywną. Na przykład model wnioskuje, że dany e-mail nie jest spamem, i rzeczywiście nie jest spamem.
wynik prawdziwie pozytywny (TP),
Przykład, w którym model prawidłowo prognozuje klasę pozytywną. Na przykład model wnioskuje, że dany e-mail to spam, i rzeczywiście tak jest.
współczynnik wyników prawdziwie pozytywnych (TPR)
Synonim słowa wycofanie. Czyli:
Współczynnik wyników prawdziwie pozytywnych jest osią Y na krzywej ROC.
TTL
Skrót od czasu życia.
U
Ultra
Model Gemini z największą liczbą parametrów. Więcej informacji znajdziesz w sekcji Gemini Ultra.
nieświadomość (w odniesieniu do atrybutu wrażliwego),
Sytuacja, w której atrybuty wrażliwe są obecne, ale nie są uwzględnione w danych treningowych. Ponieważ atrybuty wrażliwe są często skorelowane z innymi atrybutami danych, model wytrenowany bez uwzględnienia atrybutu wrażliwego może nadal mieć nierówny wpływ w odniesieniu do tego atrybutu lub naruszać inne ograniczenia dotyczące sprawiedliwości.
niedopasowanie
Utworzenie modelu o słabych możliwościach prognozowania, ponieważ nie w pełni uchwycił on złożoności danych treningowych. Niedopasowanie może być spowodowane wieloma problemami, w tym:
- Trenowanie na niewłaściwym zestawie cech.
- Trenowanie przez zbyt małą liczbę epok lub przy zbyt niskim współczynniku uczenia się.
- Trenowanie z zbyt wysokim współczynnikiem regularyzacji.
- Zbyt mała liczba warstw ukrytych w głębokiej sieci neuronowej.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie w szybkim szkoleniu z uczenia maszynowego.
undersampling
Usuwanie przykładów z klasy większościowej w zbiorze danych z nierównomiernym rozkładem klas w celu utworzenia bardziej zrównoważonego zbioru treningowego.
Rozważmy na przykład zbiór danych, w którym stosunek klasy większości do klasy mniejszości wynosi 20:1. Aby przezwyciężyć tę nierównowagę klas, możesz utworzyć zbiór treningowy składający się ze wszystkich przykładów klasy mniejszościowej, ale tylko z jednej dziesiątej przykładów klasy większościowej, co dałoby stosunek klas w zbiorze treningowym wynoszący 2:1. Dzięki podpróbkowaniu ten bardziej zrównoważony zbiór treningowy może pozwolić na utworzenie lepszego modelu. Z drugiej strony ten bardziej zrównoważony zbiór treningowy może zawierać zbyt mało przykładów, aby wytrenować skuteczny model.
Porównaj z nadpróbkowaniem.
jednokierunkowe,
System, który ocenia tylko tekst poprzedzający docelowy fragment tekstu. Z kolei system dwukierunkowy ocenia zarówno tekst, który poprzedza, jak i ten, który następuje po docelowym fragmencie tekstu. Więcej informacji znajdziesz w sekcji dwukierunkowe.
jednokierunkowy model językowy,
Model językowy, który opiera swoje prawdopodobieństwa tylko na tokenach występujących przed tokenami docelowymi, a nie po nich. W przeciwieństwie do dwukierunkowego modelu językowego.
przykład bez etykiety,
Przykład, który zawiera funkcje, ale nie ma etykiety. Na przykład w tabeli poniżej przedstawiono 3 nieoznaczone przykłady z modelu wyceny domu. Każdy z nich ma 3 cechy, ale nie ma wartości domu:
| Liczba sypialni | Liczba łazienek | Wiek domu |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
W nadzorowanym uczeniu maszynowym modele są trenowane na oznaczonych przykładach i dokonują prognoz na podstawie nieoznaczonych przykładów.
W uczeniu częściowo nadzorowanym i nienadzorowanym podczas trenowania używane są przykłady bez etykiet.
Porównaj nieoznaczony przykład z oznaczonym przykładem.
nienadzorowane uczenie maszynowe
Trenowanie modelu w celu znajdowania wzorców w zbiorze danych, zwykle w zbiorze danych bez etykiet.
Najczęstszym zastosowaniem nienadzorowanego uczenia maszynowego jest grupowanie danych w grupy podobnych przykładów. Na przykład algorytm uczenia maszynowego bez nadzoru może grupować utwory na podstawie różnych właściwości muzyki. Powstałe klastry mogą być danymi wejściowymi dla innych algorytmów uczenia maszynowego (np. dla usługi rekomendacji muzyki). Grupowanie może być przydatne, gdy brakuje przydatnych etykiet. Na przykład w przypadku domen takich jak przeciwdziałanie nadużyciom i oszustwom klastry mogą pomóc ludziom lepiej zrozumieć dane.
Porównaj z nadzorowanym uczeniem maszynowym.
Więcej informacji znajdziesz w sekcji Czym jest uczenie maszynowe? w kursie Wprowadzenie do uczenia maszynowego.
modelowanie wzrostu skuteczności,
Technika modelowania powszechnie stosowana w marketingu, która modeluje „efekt przyczynowy” (znany też jako „wpływ przyrostowy”) „leczenia” na „osobę”. Poniżej przedstawiamy dwa przykłady:
- Lekarze mogą używać modelowania przyrostowego do przewidywania spadku śmiertelności (efektu przyczynowego) w wyniku procedury medycznej (leczenia) w zależności od wieku i historii choroby pacjenta (osoby).
- Marketerzy mogą używać modelowania przyrostowego do przewidywania wzrostu prawdopodobieństwa zakupu (efektu przyczynowego) spowodowanego wyświetleniem reklamy (traktowaniem) osobie (jednostce).
Modelowanie przyrostowe różni się od klasyfikacji i regresji tym, że w modelowaniu przyrostowym zawsze brakuje niektórych etykiet (np. połowy etykiet w przypadku leczenia binarnego). Na przykład pacjent może otrzymać leczenie lub nie. Dlatego możemy obserwować, czy pacjent wyzdrowieje, czy nie, tylko w jednej z tych dwóch sytuacji (ale nigdy w obu). Główną zaletą modelu przyrostowego jest to, że może on generować prognozy dla nieobserwowanej sytuacji (przeciwstawnej hipotezy) i wykorzystywać je do obliczania efektu przyczynowego.
zwiększanie wagi,
Przypisanie do klasy próbkowanej w dół wagi równej współczynnikowi próbkowania w dół.
macierz użytkowników,
W systemach rekomendacji wektor osadzania wygenerowany przez faktoryzację macierzy, który zawiera ukryte sygnały dotyczące preferencji użytkownika. Każdy wiersz macierzy użytkowników zawiera informacje o względnej sile różnych sygnałów ukrytych w przypadku jednego użytkownika. Rozważmy na przykład system rekomendacji filmów. W tym systemie ukryte sygnały w macierzy użytkowników mogą reprezentować zainteresowanie poszczególnych użytkowników określonymi gatunkami lub mogą być trudniejszymi do zinterpretowania sygnałami, które obejmują złożone interakcje między wieloma czynnikami.
Macierz użytkowników zawiera kolumnę dla każdej cechy ukrytej i wiersz dla każdego użytkownika. Oznacza to, że macierz użytkowników ma tyle samo wierszy co macierz docelowa, która jest faktoryzowana. Na przykład w przypadku systemu rekomendacji filmów dla 1 000 000 użytkowników macierz użytkowników będzie miała 1 000 000 wierszy.
V
walidacja
Wstępna ocena jakości modelu. Weryfikacja sprawdza jakość prognoz modelu na podstawie zbioru weryfikacyjnego.
Ponieważ zbiór weryfikacyjny różni się od zbioru treningowego, weryfikacja pomaga zapobiegać przetrenowaniu.
Ocenę modelu na podstawie zbioru walidacyjnego możesz traktować jako pierwszą rundę testów, a ocenę modelu na podstawie zbioru testowego jako drugą rundę testów.
strata weryfikacji,
Dane reprezentujące stratę modelu w zbiorze weryfikacyjnym podczas określonej iteracji trenowania.
Zobacz też krzywą generalizacji.
zbiór walidacyjny,
Podzbiór zbioru danych, który przeprowadza wstępną ocenę wytrenowanego modelu. Zwykle wytrenowany model jest oceniany na podstawie zbioru walidacyjnego kilka razy, zanim zostanie oceniony na podstawie zbioru testowego.
Zwykle przykłady w zbiorze danych dzieli się na 3 odrębne podzbiory:
- zbiór treningowy,
- zbiór walidacyjny,
- zbiór testowy,
Najlepiej, aby każdy przykład w zbiorze danych należał tylko do jednego z powyższych podzbiorów. Na przykład pojedynczy przykład nie powinien należeć zarówno do zbioru treningowego, jak i do zbioru do weryfikacji.
Więcej informacji znajdziesz w sekcji Zbiory danych: dzielenie pierwotnego zbioru danych w szybkim szkoleniu z uczenia maszynowego.
uzupełnianie wartości,
Proces zastępowania brakującej wartości akceptowalnym zamiennikiem. Gdy brakuje wartości, możesz odrzucić cały przykład lub użyć imputacji wartości, aby go uratować.
Rozważmy na przykład zbiór danych zawierający cechę temperature, która powinna być rejestrowana co godzinę. Odczyt temperatury był jednak niedostępny w określonej godzinie. Oto fragment zbioru danych:
| Sygnatura czasowa | Temperatura |
|---|---|
| 1680561000 | 10 |
| 1680564600 | 12 |
| 1680568200 | brak |
| 1680571800 | 20 |
| 1680575400 | 21 |
| 1680579000 | 21 |
System może usunąć brakujący przykład lub uzupełnić brakującą temperaturę wartością 12, 16, 18 lub 20 – w zależności od algorytmu uzupełniania.
problem z zanikającym gradientem,
Tendencja gradientów wczesnych warstw ukrytych niektórych głębokich sieci neuronowych do zaskakująco płaskich (niskich). Coraz mniejsze gradienty powodują coraz mniejsze zmiany wag węzłów w głębokiej sieci neuronowej, co prowadzi do niewielkiego lub zerowego uczenia się. Modele, w których występuje problem znikającego gradientu, stają się trudne lub niemożliwe do wytrenowania. Komórki długiej pamięci krótkotrwałej rozwiązują ten problem.
Porównaj z problemem eksplodującego gradientu.
ważność zmiennych,
Zestaw wyników, który wskazuje względne znaczenie każdej cechy dla modelu.
Weźmy na przykład drzewo decyzyjne, które szacuje ceny domów. Załóżmy, że to drzewo decyzyjne korzysta z 3 cech: rozmiaru, wieku i stylu. Jeśli zestaw ważności zmiennych dla 3 cech wynosi {rozmiar=5,8, wiek=2,5, styl=4,7}, to rozmiar jest ważniejszy dla drzewa decyzyjnego niż wiek czy styl.
Istnieją różne rodzaje danych o znaczeniu zmiennych, które mogą dostarczać ekspertom ds. uczenia maszynowego informacji o różnych aspektach modeli.
wariacyjny autoenkoder (VAE),
Rodzaj autokodera, który wykorzystuje rozbieżność między danymi wejściowymi a wyjściowymi do generowania zmodyfikowanych wersji danych wejściowych. Wariacyjne autokodery są przydatne w przypadku generatywnej AI.
VAE opierają się na wnioskowaniu wariacyjnym, czyli technice szacowania parametrów modelu prawdopodobieństwa.
wektor
Bardzo przeciążone pojęcie, którego znaczenie różni się w zależności od dziedziny matematyki i nauk ścisłych. W uczeniu maszynowym wektor ma 2 właściwości:
- Typ danych: wektory w uczeniu maszynowym zwykle zawierają liczby zmiennoprzecinkowe.
- Liczba elementów: to długość wektora lub jego wymiar.
Weźmy na przykład wektor cech, który zawiera osiem liczb zmiennoprzecinkowych. Ten wektor cech ma długość lub wymiar równy 8. Pamiętaj, że wektory uczenia maszynowego często mają ogromną liczbę wymiarów.
Wektor może reprezentować wiele różnych rodzajów informacji. Na przykład:
- Każde miejsce na powierzchni Ziemi można przedstawić jako 2-wymiarowy wektor, gdzie jeden wymiar to szerokość geograficzna, a drugi to długość geograficzna.
- Obecne ceny każdego z 500 rodzajów akcji można przedstawić jako wektor 500-wymiarowy.
- Rozkład prawdopodobieństwa dla skończonej liczby klas można przedstawić jako wektor. Na przykład system klasyfikacji wieloklasowej, który przewiduje jeden z 3 kolorów wyjściowych (czerwony, zielony lub żółty), może zwrócić wektor
(0.3, 0.2, 0.5), co oznaczaP[red]=0.3, P[green]=0.2, P[yellow]=0.5.
Wektory można łączyć, dzięki czemu różne rodzaje multimediów mogą być reprezentowane jako jeden wektor. Niektóre modele działają bezpośrednio na połączeniu wielu kodowań 1 z n.
Procesory specjalistyczne, takie jak TPU, są zoptymalizowane pod kątem wykonywania operacji matematycznych na wektorach.
Vertex
Platforma Google Cloud do obsługi AI i uczenia maszynowego. Vertex udostępnia narzędzia i infrastrukturę do tworzenia, wdrażania i zarządzania aplikacjami AI, w tym dostęp do modeli Gemini.vibe coding
Wydawanie modelowi generatywnej AI poleceń tworzenia oprogramowania. Oznacza to, że prompty opisują przeznaczenie i funkcje oprogramowania, które model generatywnej AI przekłada na kod źródłowy. Wygenerowany kod nie zawsze odpowiada Twoim intencjom, dlatego kodowanie wibracyjne zwykle wymaga iteracji.
Andrej Karpathy ukuł termin „kodowanie klimatu” w tym poście na X. W poście na platformie X Karpathy opisuje ten styl jako „nowy rodzaj kodowania, w którym w pełni poddajesz się atmosferze…”. Początkowo termin ten oznaczał celowo luźne podejście do tworzenia oprogramowania, w którym nie trzeba było nawet sprawdzać wygenerowanego kodu. Jednak w wielu środowiskach termin ten szybko ewoluował i obecnie oznacza każdą formę kodu wygenerowanego przez AI.
Szczegółowy opis kodowania wibracji znajdziesz w artykule Co to jest vibe coding?
Porównaj też kodowanie wibracyjne z:
W
Funkcja straty Wassensteina
Jedna z funkcji straty powszechnie stosowanych w generatywnych sieciach przeciwstawnych, oparta na odległości między rozkładem wygenerowanych danych a rozkładem danych rzeczywistych.
waga
Wartość, przez którą model mnoży inną wartość. Trenowanie to proces określania idealnych wag modelu. Wnioskowanie to proces wykorzystywania tych wyuczonych wag do prognozowania.
Więcej informacji znajdziesz w sekcji Regresja liniowa w szybkim szkoleniu z uczenia maszynowego.
Ważona metoda naprzemiennych najmniejszych kwadratów (WALS)
Algorytm minimalizujący funkcję celu podczas faktoryzacji macierzy w systemach rekomendacji, który umożliwia zmniejszenie wagi brakujących przykładów. Algorytm WALS minimalizuje ważony błąd kwadratowy między oryginalną macierzą a rekonstrukcją, naprzemiennie ustalając faktoryzację wierszy i kolumn. Każdy z tych problemów optymalizacyjnych można rozwiązać za pomocą metody najmniejszych kwadratów w ramach optymalizacji wypukłej. Więcej informacji znajdziesz w kursie dotyczącym systemów rekomendacji.
suma ważona
Suma wszystkich odpowiednich wartości wejściowych pomnożonych przez odpowiadające im wagi. Załóżmy na przykład, że odpowiednie dane wejściowe to:
| wartość wejściowa, | waga wejściowa |
| 2 | -1,3 |
| -1 | 0,6 |
| 3 | 0,4 |
Suma ważona wynosi więc:
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
Suma ważona jest argumentem wejściowym funkcji aktywacji.
model szeroki
Model liniowy, który zwykle ma wiele rzadkich cech wejściowych. Określamy go jako „szeroki”, ponieważ taki model jest specjalnym rodzajem sieci neuronowej z dużą liczbą danych wejściowych, które są połączone bezpośrednio z węzłem wyjściowym. Modele szerokie są często łatwiejsze do debugowania i sprawdzania niż modele głębokie. Chociaż modele szerokie nie mogą wyrażać nieliniowości za pomocą warstw ukrytych, mogą używać przekształceń, takich jak łączenie cech i podział na przedziały, aby modelować nieliniowości na różne sposoby.
Kontrast z modelem głębokim.
szerokość
Liczba neuronów w określonej warstwie sieci neuronowej.
mądrość tłumu
Teoria, że uśrednianie opinii lub szacunków dużej grupy osób („tłumu”) często daje zaskakująco dobre wyniki. Weźmy na przykład grę, w której uczestnicy zgadują liczbę żelków w dużym słoiku. Chociaż większość pojedynczych odpowiedzi będzie niedokładna, średnia wszystkich odpowiedzi jest zaskakująco bliska rzeczywistej liczbie cukierków w słoiku.
Modele zespołowe to odpowiednik w oprogramowaniu koncepcji mądrości tłumu. Nawet jeśli poszczególne modele generują bardzo niedokładne prognozy, uśrednianie prognoz wielu modeli często daje zaskakująco dobre wyniki. Na przykład pojedyncze drzewo decyzyjne może dawać słabe prognozy, ale las decyzyjny często daje bardzo dobre prognozy.
wektor dystrybucyjny słowa
Reprezentowanie każdego słowa w zbiorze słów w wektorze osadzania, czyli reprezentowanie każdego słowa jako wektora wartości zmiennoprzecinkowych z zakresu od 0,0 do 1,0. Słowa o podobnym znaczeniu mają bardziej podobne reprezentacje niż słowa o różnym znaczeniu. Na przykład marchewki, seler i ogórki będą miały stosunkowo podobne reprezentacje, które będą się znacznie różnić od reprezentacji samolotu, okularów przeciwsłonecznych i pasty do zębów.
X
XLA (Accelerated Linear Algebra)
Kompilator uczenia maszynowego open source dla procesorów graficznych, procesorów i akceleratorów uczenia maszynowego.
Kompilator XLA pobiera modele z popularnych platform ML, takich jak PyTorch, TensorFlow i JAX, i optymalizuje je pod kątem wykonywania z wysoką wydajnością na różnych platformach sprzętowych, w tym na procesorach graficznych, procesorach i akceleratorach ML.
Z
uczenie „zero-shot”
Rodzaj trenowania uczenia maszynowego, w którym model wyciąga prognozę dla zadania, do którego nie został wcześniej wytrenowany. Innymi słowy, model nie otrzymuje żadnych przykładów trenowania pod kątem konkretnego zadania, ale ma wykonać wnioskowanie w ramach tego zadania.
prompty „zero-shot”
Prompt, który nie zawiera przykładu tego, jak ma odpowiadać duży model językowy. Na przykład:
| Elementy jednego promptu | Uwagi |
|---|---|
| Jaka jest oficjalna waluta w wybranym kraju? | Pytanie, na które ma odpowiedzieć LLM. |
| Indie: | Faktyczne zapytanie. |
Duży model językowy może odpowiedzieć w jeden z tych sposobów:
- Rupia
- INR
- ₹
- Rupia indyjska
- rupia,
- Rupia indyjska
Wszystkie odpowiedzi są prawidłowe, ale możesz preferować określony format.
Porównaj promptowanie bez przykładów z tymi terminami:
Normalizacja standaryzacji Z
Technika skalowania, która zastępuje surową wartość cechy wartością zmiennoprzecinkową reprezentującą liczbę odchyleń standardowych od średniej tej cechy. Weźmy na przykład cechę, której średnia wynosi 800, a odchylenie standardowe – 100. W tabeli poniżej pokazujemy, jak normalizacja za pomocą wyniku z (Z-score) mapuje wartość pierwotną na wynik z:
| Wartość nieprzetworzona | Standaryzacja Z |
|---|---|
| 800 | 0 |
| 950 | +1,5 |
| 575 | -2,25 |
Model uczenia maszynowego jest następnie trenowany na podstawie wyników z-score dla tej cechy, a nie na podstawie wartości surowych.
Więcej informacji znajdziesz w sekcji Dane liczbowe: normalizacja w kursie Machine Learning Crash Course.
Ten glosariusz zawiera definicje terminów związanych z uczeniem maszynowym.