Binning (nazywany też grupowaniem) to
inżynieria cech
polegającą na grupowaniu różnych podzakresów liczbowych w przedziały lub
zasobników.
W wielu przypadkach łączenie przekształca dane liczbowe w dane kategorialne.
Weźmy na przykład funkcję
o nazwie X, której najniższa wartość to 15 i
najwyższa wartość to 425. Korzystając z binning, możesz reprezentować X za pomocą
5 przedziałów koszyka:
- Przedział 1: od 15 do 34
- Kosz 2: od 35 do 117
- Przedział 3: 118–279
- Przedział 4: od 280 do 392
- Kosz 5: od 393 do 425
Przedział 1 obejmuje zakres od 15 do 34, więc każda wartość X od 15 do 34
trafią do kontenera 1. Model wytrenowany na tych przedziałach nie będzie reagować inaczej
na wartości X 17 i 29, ponieważ obie wartości znajdują się w przedziale 1.
Wektor cech reprezentuje te pięć przedziałów:
| Numer przedziału | Zakres | Wektor cech |
|---|---|---|
| 1 | 15-34 | [1,0, 0,0, 0,0, 0,0, 0,0] |
| 2 | 35-117 | [0,0, 1,0, 0,0, 0,0, 0,0] |
| 3 | 118-279 | [0,0, 0,0, 1,0, 0,0, 0,0] |
| 4 | 280-392 | [0,0, 0,0, 0,0, 1,0, 0,0] |
| 5 | 393-425 | [0,0, 0,0, 0,0, 0,0, 1,0] |
Mimo że X jest pojedynczą kolumną w zbiorze danych, powiązanie powoduje, że model
aby traktować X jako 5 osobnych funkcji. Dzięki temu model uczy się
dla każdego przedziału.
Binning to dobra alternatywa dla skalowania lub przycinanie, gdy jeden z są spełnione następujące warunki:
- Ogólny zależność liniowa między obiektem a obiektem Etykieta jest słaba lub nie istnieje.
- Gdy wartości cech są grupowane.
Binning może wydawać się sprzeczny z intuicją, ponieważ model w modelu poprzedni przykład traktuje wartości 37 i 115 jednakowo. Ale gdy obiekt wydaje się bardziej nierówny niż liniowy, powiązanie to znacznie lepszy sposób przedstawiają dane.
Przykład Bining: liczba kupujących a temperatura
Załóżmy, że tworzysz model, który prognozuje liczbę temperatury na zewnątrz w danym dniu. Oto fabuła a także liczbę kupujących.
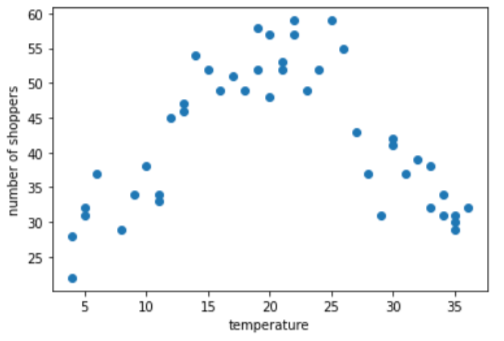
Nie dziwi więc, że liczba kupujących była najwyższa w chwili, gdy była najkorzystniejsza temperatura.
Tę funkcję możesz przedstawić w postaci nieprzetworzonych wartości, czyli temperatury 35,0 będzie to 35,0 w wektorze cech. Czy to najlepszy pomysł?
Podczas trenowania model regresji liniowej uczy się jednej wagi dla każdej funkcji. Dlatego, jeśli temperatura jest przedstawiana jako jedna cecha, temperatura równa 35,0 będzie miała pięciokrotnie większy wpływ (czyli jedną piątą wpływ) w prognozie jako temperatura 7,0. Jednak fabuła żadnych relacji liniowej między etykietą a wartość cechy.
Wykres sugeruje trzy klastry w następujących podzakresach:
- Przedział 1 to zakres temperatur z zakresu 4–11.
- Przedział 2 to zakres temperatur z zakresu 12–26.
- Przedział 3 to zakres temperatur z zakresu 27–36.

Model uczy się oddzielnych wag dla każdego przedziału.
Mimo że można utworzyć więcej niż trzy przedziały, nawet osobny przedział na każdy odczyt temperatury jest niekorzystny z następujących powodów:
- Model może nauczyć się powiązania między przedziałem a etykietą tylko wtedy, gdy masz w nim wystarczającą liczbę przykładów. W tym przykładzie każdy z 3 przedziałów zawiera co najmniej 10 przykładów, co może wystarczyć do trenowania. Zawiera 33 oddzielne pojemniki żaden z zasobników nie zawierałby wystarczającej liczby przykładów do trenowania modelu.
- Osobne pojemniki na każdą temperaturę przynoszą 33 osobne funkcje temperatury. Zazwyczaj należy jednak zminimalizować liczby cech w modelu.
Ćwiczenie: sprawdź swoją wiedzę
Ten wykres przedstawia medianę ceny domu dla każdego 0,2 stopnia szerokość geograficzna mitycznego kraju Freedonia:
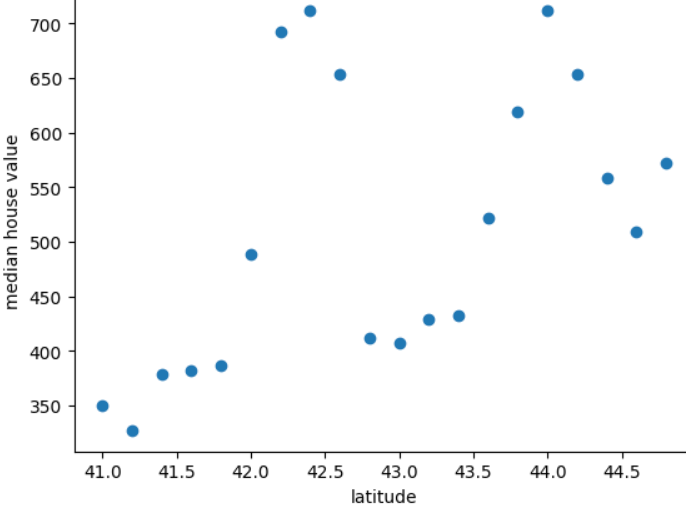
Grafika przedstawia nieliniowy wzorzec między wartością początkową a szerokością geograficzną. więc określenie szerokości geograficznej jako wartości zmiennoprzecinkowej jest mało prawdopodobne i generują dobre prognozy. Być może jednak lepszym rozwiązaniem byłby podział szerokości geograficznej co?
- 41,0 do 41,8
- 42,0 do 42,6
- 42,8 do 43,4
- 43,6 do 44,8
Grupowanie kwantylowe
Grupowanie kwantowe tworzy granice grupowania, dzięki czemu liczba przykładów w każdym segmencie jest dokładnie lub prawie równa. Segmentowanie kwantylowe ukrywa głównie te odstające.
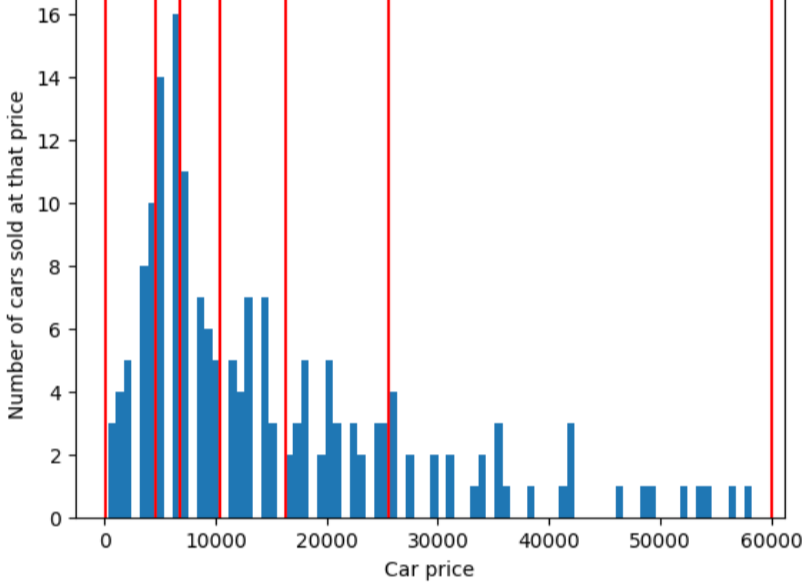
Aby zilustrować problem, który rozwiązuje zasobnik kwantylowy, rozważ zasobniki o równych odstępach pokazane na ilustracji poniżej, z dziesięciu zasobników to dokładnie 10 tys. dolarów. Zwróć uwagę,że zasobnik od 0 do 10 000 zawiera dziesiątki przykładów ale zasobnik od 50 000 do 60 000 zawiera tylko 5 przykładów. Model ma więc wystarczającą liczbę przykładów, aby trenować na przedziałach od 0 do 10 tys. ale za mało przykładów, aby można było je wytrenować dla 50–60 tys. zasobników.
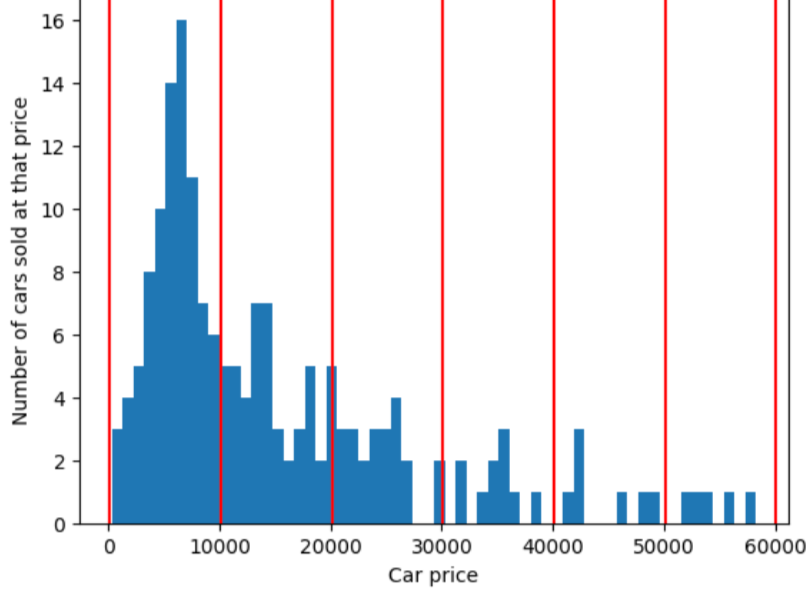
Na przykład poniższy rysunek używa grupowania kwantylowego do dzielenia cen samochodów do kosza z mniej więcej taką samą liczbą przykładów w każdym zasobniku. Zwróć uwagę, że niektóre pojemniki mają wąski przedział cenowy, a inne mają bardzo szeroki zakres cenowy.