Strata to wartość liczbowa, która opisuje, jak bardzo prognozy modelu są błędne. Funkcja straty mierzy odległość między prognozami modelu a rzeczywistymi etykietami. Celem trenowania modelu jest minimalizowanie straty, czyli zmniejszanie jej do najniższej możliwej wartości.
Na poniższym obrazie możesz zobaczyć funkcję straty jako strzałki narysowane od punktów danych do modelu. Strzałki pokazują, jak bardzo prognozy modelu odbiegają od rzeczywistych wartości.
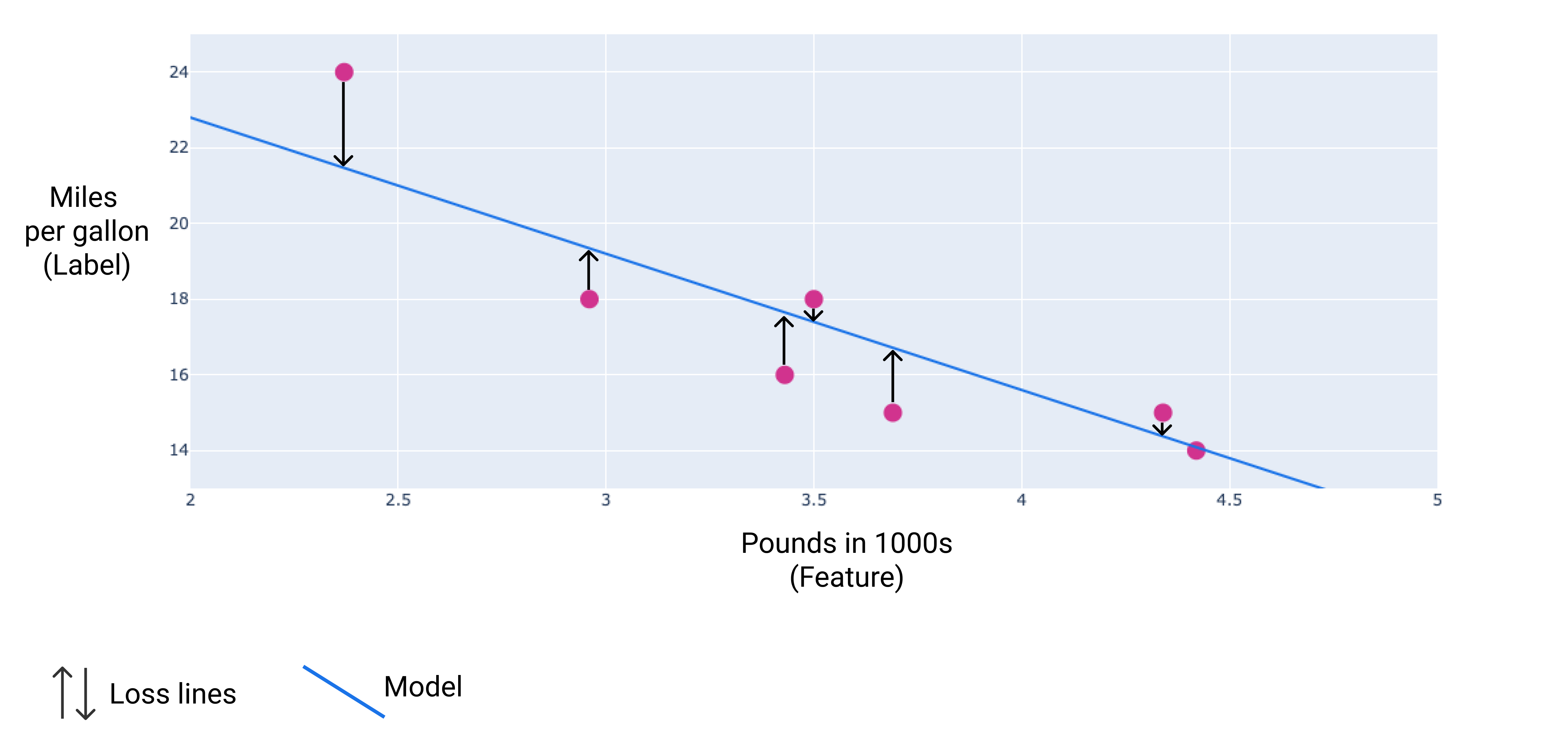
Rysunek 8. Utrata jest mierzona od wartości rzeczywistej do wartości przewidywanej.
Odległość utraty
W statystyce i uczeniu maszynowym funkcja straty mierzy różnicę między wartościami prognozowanymi a rzeczywistymi. Funkcja straty koncentruje się na odległości między wartościami, a nie na kierunku. Jeśli np. model przewiduje wartość 2, a rzeczywista wartość to 5, nie interesuje nas, że strata jest ujemna (2 – 5 = –3). Zamiast tego interesuje nas odległość między wartościami, która wynosi 3. Dlatego wszystkie metody obliczania straty usuwają znak.
Oto 2 najczęstsze metody usuwania znaku:
- Oblicz wartość bezwzględną różnicy między wartością rzeczywistą a prognozą.
- Podnieś do kwadratu różnicę między wartością rzeczywistą a prognozą.
Rodzaje strat
W regresji liniowej występuje 5 głównych typów funkcji straty, które zostały opisane w tej tabeli.
| Typ straty | Definicja | Równanie |
|---|---|---|
| Utrata sygnału L1 | Suma wartości bezwzględnych różnicy między prognozowanymi a rzeczywistymi wartościami. | $ ∑ | actual\ value - predicted\ value | $ |
| Średni błąd bezwzględny (MAE) | Średnia strat L1 w przypadku zbioru N przykładów. | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| Utrata L2 | Suma kwadratów różnic między prognozowanymi a rzeczywistymi wartościami. | $ ∑(wartość\ rzeczywista - wartość\ przewidywana)^2 $ |
| Błąd średniokwadratowy (MSE) | Średnia strat L2 w przypadku zbioru N przykładów. | $ \frac{1}{N} ∑ (rzeczywista\ wartość - przewidywana\ wartość)^2 $ |
| Średnia kwadratowa błędów (RMSE) | Pierwiastek kwadratowy z błędu średniokwadratowego (MSE). | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
Funkcjonalna różnica między funkcją straty L1 a funkcją straty L2 (lub między MAE/RMSE a MSE) polega na podnoszeniu do kwadratu. Gdy różnica między prognozą a etykietą jest duża, podniesienie do kwadratu jeszcze bardziej zwiększa stratę. Gdy różnica jest niewielka (mniejsza niż 1), podniesienie do kwadratu jeszcze bardziej zmniejsza stratę.
W niektórych przypadkach użycia wskaźniki utraty, takie jak MAE i RMSE, mogą być lepsze niż utrata L2 lub MSE, ponieważ są bardziej zrozumiałe dla człowieka. Mierzą one błąd w tej samej skali co przewidywana wartość modelu.
Podczas przetwarzania wielu przykładów naraz zalecamy uśrednianie strat we wszystkich przykładach, niezależnie od tego, czy używasz MAE, MSE czy RMSE.
Przykład obliczania strat
Korzystając z poprzedniej linii najlepszego dopasowania, obliczymy stratę L2 dla pojedynczego przykładu. Z linii najlepszego dopasowania uzyskaliśmy te wartości wagi i odchylenia:
- $ \small{Waga: -4.6} $
- $ \small{Odchylenie: 34} $
Jeśli model przewiduje, że samochód o masie 2370 funtów zużywa 23,1 mili na galon, a w rzeczywistości zużywa 26 mili na galon, stratę L2 obliczymy w ten sposób:
| Wartość | Równanie | Wynik |
|---|---|---|
| Prognoza | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Rzeczywista wartość | $ \small{ label } $ | $ \small{ 26 } $ |
| Strata L2 | $ \small{ (wartość\ rzeczywista - wartość\ przewidywana)^2 } $ $\small{ (26 - 23,1)^2 }$ |
$\small{8.41}$ |
W tym przykładzie strata L2 dla tego pojedynczego punktu danych wynosi 8, 41.
Wybieranie utraty
Decyzja o użyciu MAE lub MSE może zależeć od zbioru danych i sposobu, w jaki chcesz traktować określone prognozy. Większość wartości cech w zbiorze danych zwykle mieści się w określonym zakresie. Na przykład samochody ważą zwykle od 2000 do 5000 funtów i przejeżdżają od 8 do 50 mil na galon. Samochód o masie 8000 funtów lub samochód, który przejeżdża 100 mil na galonie, wykracza poza typowy zakres i zostałby uznany za wartość odstającą.
Wartość odstająca może też odnosić się do tego, jak bardzo prognozy modelu odbiegają od rzeczywistych wartości. Na przykład 3000 funtów mieści się w typowym zakresie wagi samochodu, a 40 mil na galon mieści się w typowym zakresie zużycia paliwa. Jednak samochód o wadze 1360 kg, który przejeżdża 64 km na 3,8 l paliwa, byłby wartością odstającą w prognozie modelu, ponieważ model przewiduje, że samochód o wadze 1360 kg przejeżdża około 32 km na 3,8 l paliwa.
Wybierając najlepszą funkcję straty, zastanów się, jak chcesz, aby model traktował wartości odstające. Na przykład MSE przesuwa model w stronę wartości odstających, a MAE nie. Funkcja straty L2 nakłada na wartość odstającą znacznie większą karę niż funkcja straty L1. Na przykład poniższe obrazy przedstawiają model wytrenowany przy użyciu MAE i model wytrenowany przy użyciu MSE. Czerwona linia reprezentuje w pełni wytrenowany model, który będzie używany do tworzenia prognoz. Wartości odstające są bliższe modelowi wytrenowanemu za pomocą MSE niż modelowi wytrenowanemu za pomocą MAE.
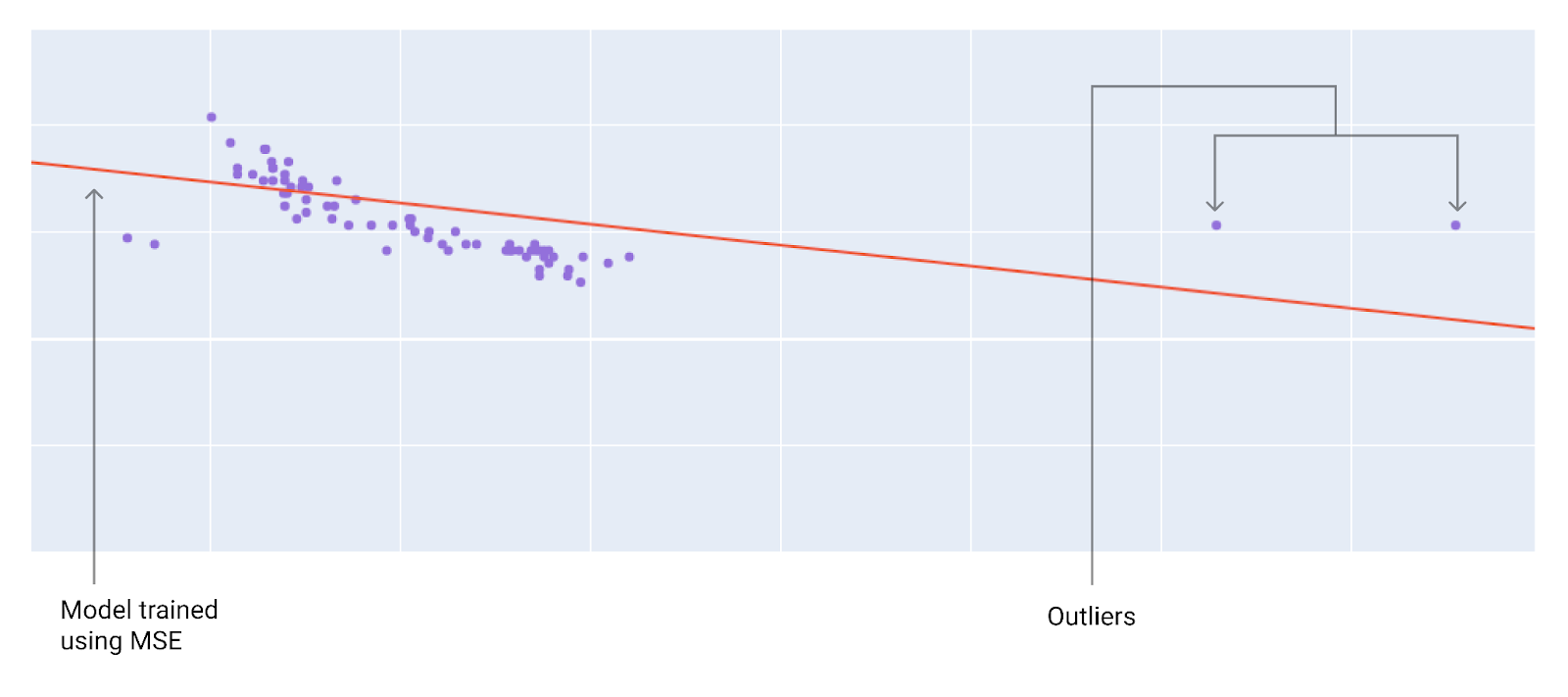
Rysunek 9. Funkcja straty MSE przybliża model do wartości odstających.
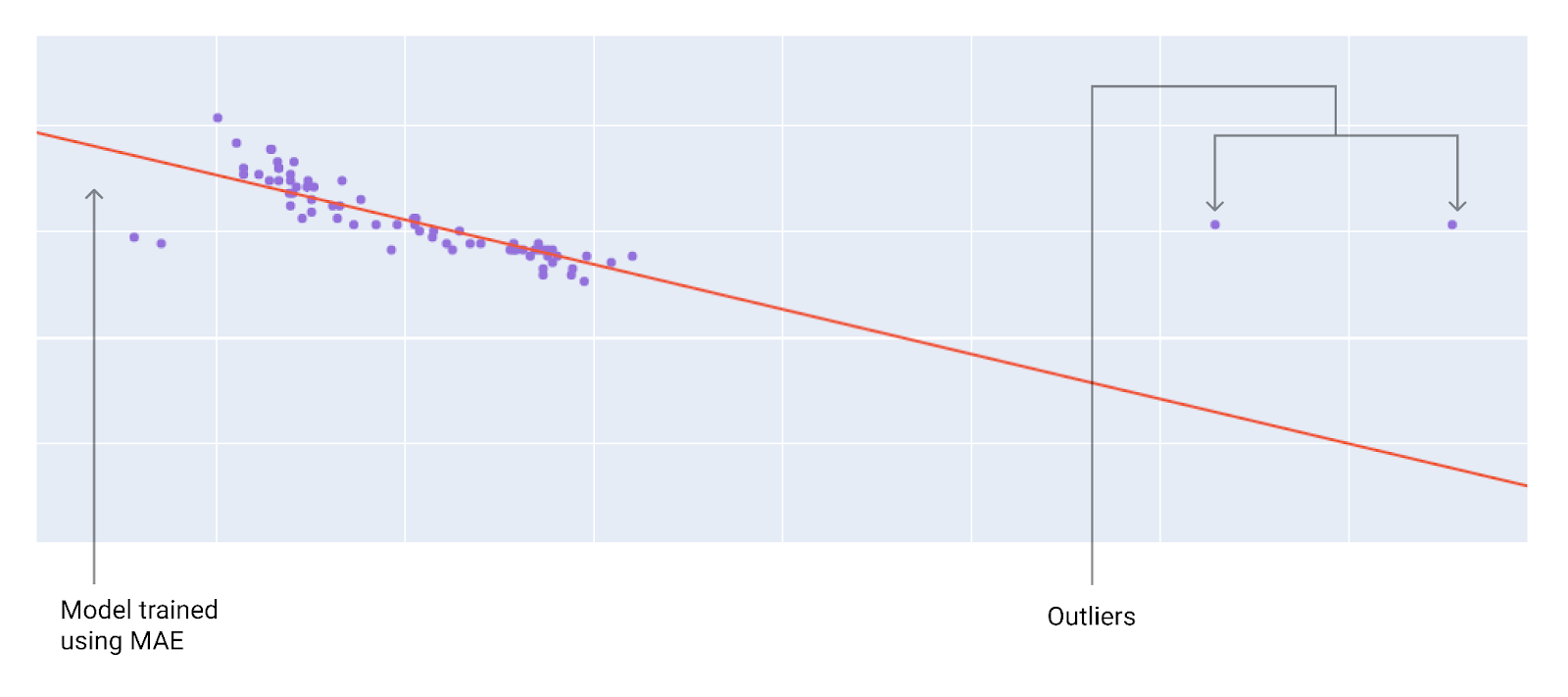
Rysunek 10. Funkcja straty MAE utrzymuje model z dala od wartości odstających.
Zwróć uwagę na związek między modelem a danymi:
MSE Model jest bliżej wartości odstających, ale dalej od większości pozostałych punktów danych.
MAE Model jest bardziej oddalony od wartości odstających, ale bliżej większości pozostałych punktów danych.
Sprawdź swoją wiedzę
Rozważmy te 2 wykresy modelu liniowego dopasowanego do zbioru danych:
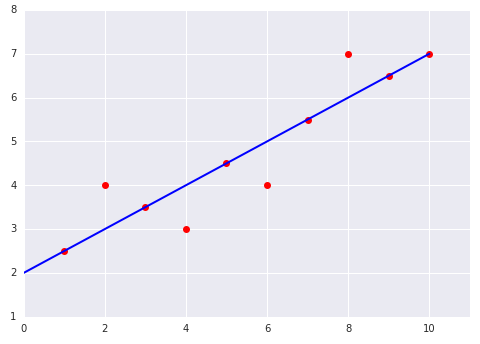
|
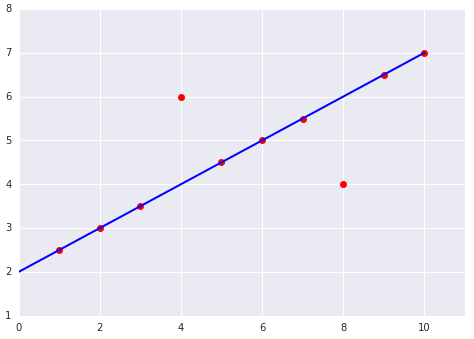
|
