„Alle Modelle sind falsch, aber einige sind nützlich.“ – George Box, 1978
Statistische Verfahren sind zwar leistungsstark, haben aber auch ihre Grenzen. Wenn Forscher diese Einschränkungen kennen, können sie Fehler und ungenaue Behauptungen vermeiden, wie die von BF Skinner, dass Shakespeare Alliteration nicht häufiger verwendet hat, als es der Zufall vorraussagen würde. (Die Studie von Skinner war nicht leistungsstark.1)
Unsicherheit und Fehlerbalken
Es ist wichtig, Unsicherheiten in Ihrer Analyse anzugeben. Es ist ebenso wichtig, die Unsicherheit in den Analysen anderer zu quantifizieren. Datenpunkte, die in einem Diagramm einen Trend darstellen, aber sich überschneidende Fehlerbalken haben, deuten möglicherweise gar nicht auf ein Muster hin. Die Unsicherheit kann auch zu hoch sein, um aus einer bestimmten Studie oder einem statistischen Test nützliche Schlussfolgerungen zu ziehen. Wenn für eine Forschungsstudie eine Genauigkeit auf Parzellenebene erforderlich ist, ist ein georeferenzierter Datensatz mit einer Unsicherheit von +/- 500 m zu ungenau, um verwendet zu werden.
Alternativ können Unsicherheitsgrade bei Entscheidungsprozessen nützlich sein. Daten, die eine bestimmte Wasseraufbereitung mit einer Unsicherheit von 20% bei den Ergebnissen unterstützen, können zu einer Empfehlung für die Implementierung dieser Wasseraufbereitung mit fortlaufender Überwachung des Programms zur Behebung dieser Unsicherheit führen.
Bayesianische neuronale Netze können die Unsicherheit quantifizieren, indem sie Verteilungen von Werten anstelle von Einzelwerten vorhersagen.
Irrelevanz
Wie bereits in der Einführung erwähnt, gibt es immer mindestens eine kleine Lücke zwischen Daten und Realität. Der versierte ML-Experte sollte feststellen, ob der Datensatz für die gestellte Frage relevant ist.
Huff beschreibt eine frühe Studie zur öffentlichen Meinung, in der festgestellt wurde, dass die Antworten weißer Amerikaner auf die Frage, wie einfach es für schwarze Amerikaner war, ihren Lebensunterhalt zu verdienen, direkt und umgekehrt mit ihrem Mitgefühl für schwarze Amerikaner zusammenhängen. Je stärker die rassistische Feindseligkeit zunahm, desto optimistischer wurden die Antworten auf die erwarteten wirtschaftlichen Chancen. Das könnte als Zeichen für Fortschritte missverstanden worden sein. Die Studie konnte jedoch nichts über die tatsächlichen wirtschaftlichen Möglichkeiten aussagen, die Schwarzen Amerikanern damals zur Verfügung standen, und eignete sich nicht, um Rückschlüsse auf die Realität des Arbeitsmarktes zu ziehen – nur auf die Meinungen der Umfrageteilnehmer. Die erhobenen Daten waren für die Situation auf dem Arbeitsmarkt irrelevant.2
Sie könnten ein Modell mit Umfragedaten wie den oben beschriebenen trainieren, bei denen die Ausgabe tatsächlich Optimismus und nicht Chancen misst. Da vorhergesagte Chancen jedoch für tatsächliche Chancen irrelevant sind, würden Sie die Vorhersagen des Modells falsch darstellen, wenn Sie behaupten würden, dass das Modell tatsächliche Chancen vorhersagt.
Störfaktoren
Eine Störvariable, Störung oder Kofaktor ist eine Variable, die nicht untersucht wird, aber die untersuchten Variablen beeinflusst und die Ergebnisse verfälschen kann. Nehmen wir beispielsweise ein ML-Modell an, das die Sterblichkeitsraten für ein Eingabeland anhand von Merkmalen der Gesundheitspolitik vorhersagt. Angenommen, der Median ist keine Funktion. Angenommen, einige Länder haben eine ältere Bevölkerung als andere. Da die Kontrollvariable „Medianalter“ ignoriert wird, könnten mit diesem Modell fehlerhafte Sterblichkeitsraten vorhergesagt werden.
In den USA ist die ethnische Zugehörigkeit oft stark mit der sozioökonomischen Schicht korreliert, obwohl nur die ethnische Zugehörigkeit und nicht die Schicht in den Sterbefalldaten erfasst wird. Schichtbezogene Störfaktoren wie Zugang zu Gesundheitsversorgung, Ernährung, gefährliche Arbeit und sicheres Wohnen können einen stärkeren Einfluss auf die Sterblichkeitsraten haben als die ethnische Zugehörigkeit, werden aber vernachlässigt, weil sie nicht in den Datensätzen enthalten sind.3 Die Identifizierung und Kontrolle dieser Störfaktoren ist entscheidend, um nützliche Modelle zu erstellen und aussagekräftige und korrekte Schlussfolgerungen zu ziehen.
Wenn ein Modell mit vorhandenen Sterblichkeitsdaten trainiert wird, die die ethnische Zugehörigkeit, aber nicht die soziale Schicht umfassen, kann es die Sterblichkeit anhand der ethnischen Zugehörigkeit vorhersagen, auch wenn die soziale Schicht ein stärkerer Prädiktor für die Sterblichkeit ist. Dies kann zu ungenauen Annahmen zur Kausalität und ungenauen Vorhersagen zur Sterblichkeit von Patienten führen. ML-Experten sollten prüfen, ob es in ihren Daten Störfaktoren gibt, und welche aussagekräftigen Variablen in ihrem Datensatz möglicherweise fehlen.
1985 wurde in der Nurses' Health Study, einer Beobachtungskohorte der Harvard Medical School und der Harvard School of Public Health, festgestellt, dass die Kohorte, die eine Östrogenersatztherapie durchlief, weniger Herzinfarkte aufwies als die Kohorte, die nie Östrogen einnahm. Daher verschrieben Ärzte ihren menopausalen und postmenopausalen Patienten jahrzehntelang Östrogen, bis eine klinische Studie im Jahr 2002 Gesundheitsrisiken durch eine langfristige Östrogentherapie aufzeigte. Die Praxis, Östrogene für postmenopausale Frauen zu verschreiben, wurde eingestellt, nicht jedoch, bevor sie zu geschätzten zehntausenden vorzeitigen Todesfällen geführt hatte.
Mehrere Störfaktoren könnten die Assoziation verursacht haben. Epidemiologen haben festgestellt, dass Frauen, die eine Hormonersatztherapie erhalten, im Vergleich zu Frauen, die keine erhalten, in der Regel schlanker, besser ausgebildet, wohlhabender, gesundheitsbewusster und eher sportlich aktiv sind. In verschiedenen Studien wurde festgestellt, dass Bildung und Wohlstand das Risiko von Herzerkrankungen senken. Diese Effekte hätten die scheinbare Korrelation zwischen Östrogentherapie und Herzinfarkten verfälscht.4
Prozentsätze mit negativen Zahlen
Vermeiden Sie die Verwendung von Prozentsätzen, wenn negative Zahlen vorhanden sind,5 da alle Arten von signifikanten Gewinnen und Verlusten verschleiert werden können. Angenommen, die Restaurantbranche bietet 2 Millionen Arbeitsplätze. Wenn die Branche Ende März 2020 eine Million dieser Arbeitsplätze verliert, zehn Monate lang keine Nettoänderung verzeichnet und Anfang Februar 2021 900.000 Arbeitsplätze wiedergewonnen hat, würde ein Vergleich zum Vorjahr Anfang März 2021 nur einen Verlust von 5% der Arbeitsplätze in der Gastronomie anzeigen. Angenommen, es gibt keine anderen Änderungen, würde ein Vergleich zum Vorjahr Ende April 2021 eine Steigerung der Stellenangebote in der Gastronomie um 90% nahelegen. Das ist ein ganz anderes Bild der Realität.
Verwenden Sie nach Möglichkeit tatsächliche Zahlen, die gegebenenfalls normalisiert werden. Weitere Informationen finden Sie unter Mit numerischen Daten arbeiten.
Post-hoc-Falle und unbrauchbare Korrelationen
Der Post-hoc-Fehler ist die Annahme, dass Ereignis A Ereignis B verursacht hat, weil Ereignis A auf Ereignis B folgte. Einfacher ausgedrückt: Es wird eine Ursache-Wirkungs-Beziehung angenommen, die nicht existiert. Noch einfacher ausgedrückt: Korrelationen beweisen keine Kausalität.
Neben einer klaren Ursache-Wirkungs-Beziehung können Korrelationen auch aus folgenden Gründen entstehen:
- Reiner Zufall (siehe Spurious correlations von Tyler Vigen für Illustrationen, einschließlich einer starken Korrelation zwischen der Scheidungsrate in Maine und dem Margarinekonsum).
- Eine reale Beziehung zwischen zwei Variablen, wobei unklar bleibt, welche Variable ursächlich ist und welche davon betroffen ist.
- Eine dritte, separate Ursache, die beide Variablen beeinflusst, obwohl die korrelierten Variablen miteinander in keinem Zusammenhang stehen. Die globale Inflation kann beispielsweise die Preise sowohl für Yachten als auch für Sellerie erhöhen.6
Es ist auch riskant, eine Korrelation über die vorhandenen Daten hinaus zu extrapolieren. Huff weist darauf hin, dass etwas Regen die Ernte verbessert, zu viel Regen sie jedoch beschädigt. Die Beziehung zwischen Regen und Ernte ist also nicht linear.7 (Weitere Informationen zu nichtlinearen Beziehungen finden Sie in den nächsten beiden Abschnitten.) Jones weist darauf hin, dass die Welt voller unvorhersehbarer Ereignisse wie Krieg und Hungersnot ist, die zukünftige Prognosen von Zeitreihendaten mit enormen Unsicherheiten belasten.8
Außerdem ist selbst eine echte Korrelation, die auf Ursache und Wirkung basiert, möglicherweise nicht hilfreich für die Entscheidungsfindung. Huff nennt als Beispiel die Korrelation zwischen Heiratsfähigkeit und Hochschulausbildung in den 1950er-Jahren. Frauen, die eine Hochschule besuchten, heirateten seltener, aber es könnte auch sein, dass Frauen, die eine Hochschule besuchten, von vornherein weniger zur Ehe bereit waren. In diesem Fall veränderte ein Hochschulabschluss die Wahrscheinlichkeit, dass sie heiraten, nicht.9
Wenn eine Analyse eine Korrelation zwischen zwei Variablen in einem Datensatz erkennt, stellen Sie sich folgende Fragen:
- Um welche Art von Korrelation handelt es sich: um eine Ursache-Wirkungs-Beziehung, eine Scheinkorrelation, eine unbekannte Beziehung oder eine durch eine dritte Variable verursachte Beziehung?
- Wie riskant ist die Extrapolation aus den Daten? Jede Modellvorhersage für Daten, die nicht im Trainingsdatensatz enthalten sind, ist im Grunde eine Interpolation oder Extrapolation aus den Daten.
- Kann die Korrelation verwendet werden, um fundierte Entscheidungen zu treffen? Optimismus könnte beispielsweise stark mit steigenden Löhnen korrelieren. Die Stimmungsanalyse eines großen Korpus an Textdaten, z. B. von Social-Media-Beiträgen von Nutzern in einem bestimmten Land, wäre jedoch nicht hilfreich, um Lohnerhöhungen in diesem Land vorherzusagen.
Beim Trainieren eines Modells suchen ML-Experten in der Regel nach Merkmalen, die stark mit dem Label korrelieren. Wenn die Beziehung zwischen den Features und dem Label nicht gut verstanden wird, kann dies zu den in diesem Abschnitt beschriebenen Problemen führen, einschließlich Modellen, die auf falschen Korrelationen basieren, und Modellen, die davon ausgehen, dass sich bisherige Trends in Zukunft fortsetzen, was aber nicht der Fall ist.
Die lineare Verzerrung
In „Linear Thinking in a Nonlinear World“ beschreiben Bart de Langhe, Stefano Puntoni und Richard Larrick die lineare Verzerrung als die Tendenz des menschlichen Gehirns, lineare Beziehungen zu erwarten und zu suchen, obwohl viele Phänomene nicht linear sind. Die Beziehung zwischen den Einstellungen und dem Verhalten von Menschen ist beispielsweise eine konvexe Kurve und keine Linie. In einem Artikel von 2007 im Journal of Consumer Policy, der von de Langhe et al. zitiert wird, Jenny van Doorn et al. haben den Zusammenhang zwischen der Sorge der Umfrageteilnehmer um die Umwelt und dem Kauf von Bioprodukten modelliert. Diejenigen mit den größten Bedenken hinsichtlich der Umwelt kauften mehr Bioprodukte, aber es gab nur sehr geringe Unterschiede zwischen allen anderen Befragten.
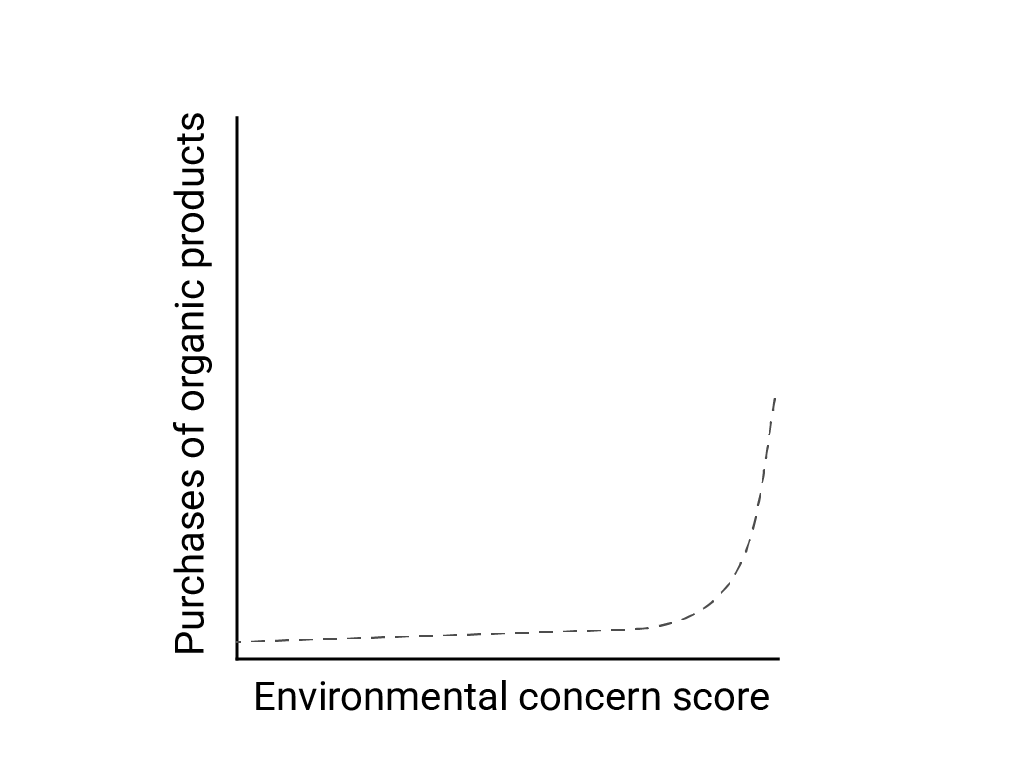
Berücksichtigen Sie beim Entwerfen von Modellen oder Studien die Möglichkeit nichtlinearer Beziehungen. Da bei A/B-Tests nichtlineare Beziehungen übersehen werden können, sollten Sie auch eine dritte, mittlere Bedingung (C) testen. Überlegen Sie auch, ob das anfänglich linear erscheinende Verhalten auch in Zukunft linear sein wird oder ob zukünftige Daten eher logarithmisch oder anderweitig nicht linear sein könnten.
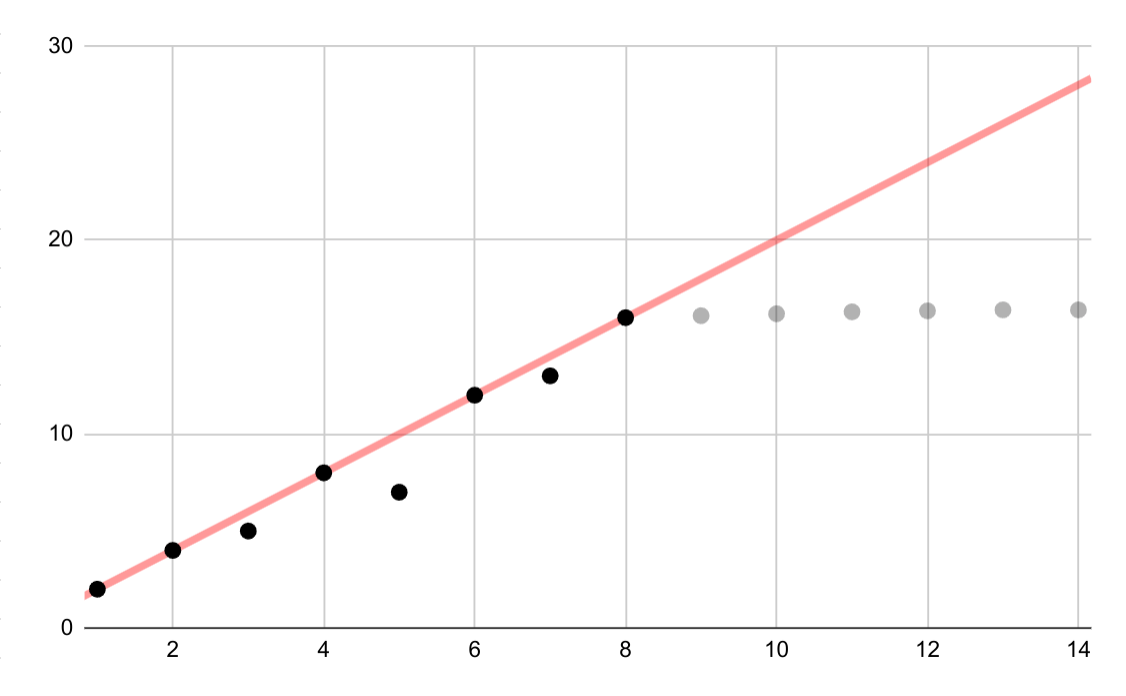
Dieses hypothetische Beispiel zeigt eine fehlerhafte lineare Anpassung für logarithmische Daten. Wenn nur die ersten Datenpunkte verfügbar wären, wäre es sowohl verlockend als auch falsch, eine fortlaufende lineare Beziehung zwischen den Variablen anzunehmen.
Lineare Interpolation
Prüfen Sie alle Interpolationen zwischen Datenpunkten, da durch Interpolation fiktive Punkte eingeführt werden und die Intervalle zwischen den tatsächlichen Messungen signifikante Schwankungen enthalten können. Betrachten Sie als Beispiel die folgende Visualisierung von vier Datenpunkten, die durch lineare Interpolationen verbunden sind:

Sehen wir uns nun ein Beispiel für Schwankungen zwischen Datenpunkten an, die durch eine lineare Interpolation ausgelöscht werden:
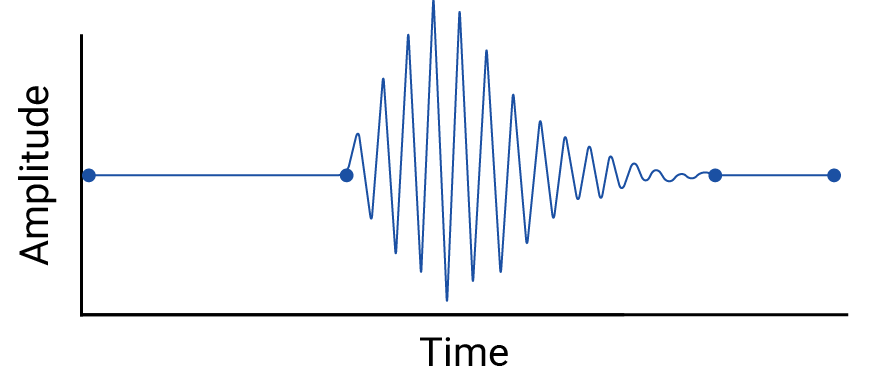
Das Beispiel ist erfunden, da Seismographen kontinuierlich Daten erfassen und dieses Erdbeben daher nicht übersehen würde. Es ist jedoch nützlich, um die Annahmen zu veranschaulichen, die bei Interpolationen getroffen werden, und die realen Phänomene, die Datenpraktiker möglicherweise übersehen.
Runge-Phänomen
Das Runge-Phänomen, auch als „polynomiale Wiggle“ bezeichnet, ist ein Problem am anderen Ende des Spektrums von linearer Interpolation und linearer Voreingenommenheit. Wenn Sie eine polynome Interpolation an Daten anpassen, kann es vorkommen, dass Sie einen Polynom mit zu hohem Grad verwenden. Der Grad ist der höchste Exponent in der polynomen Gleichung. Dies führt zu merkwürdigen Schwankungen an den Rändern. Wenn Sie beispielsweise eine Polynominterpolation vom Grad 11 auf ungefähr lineare Daten anwenden, d. h., der Term mit der höchsten Ordnung in der Polynomgleichung hat den Wert \(x^{11}\), führt dies zu bemerkenswert schlechten Vorhersagen am Anfang und Ende des Datenbereichs:
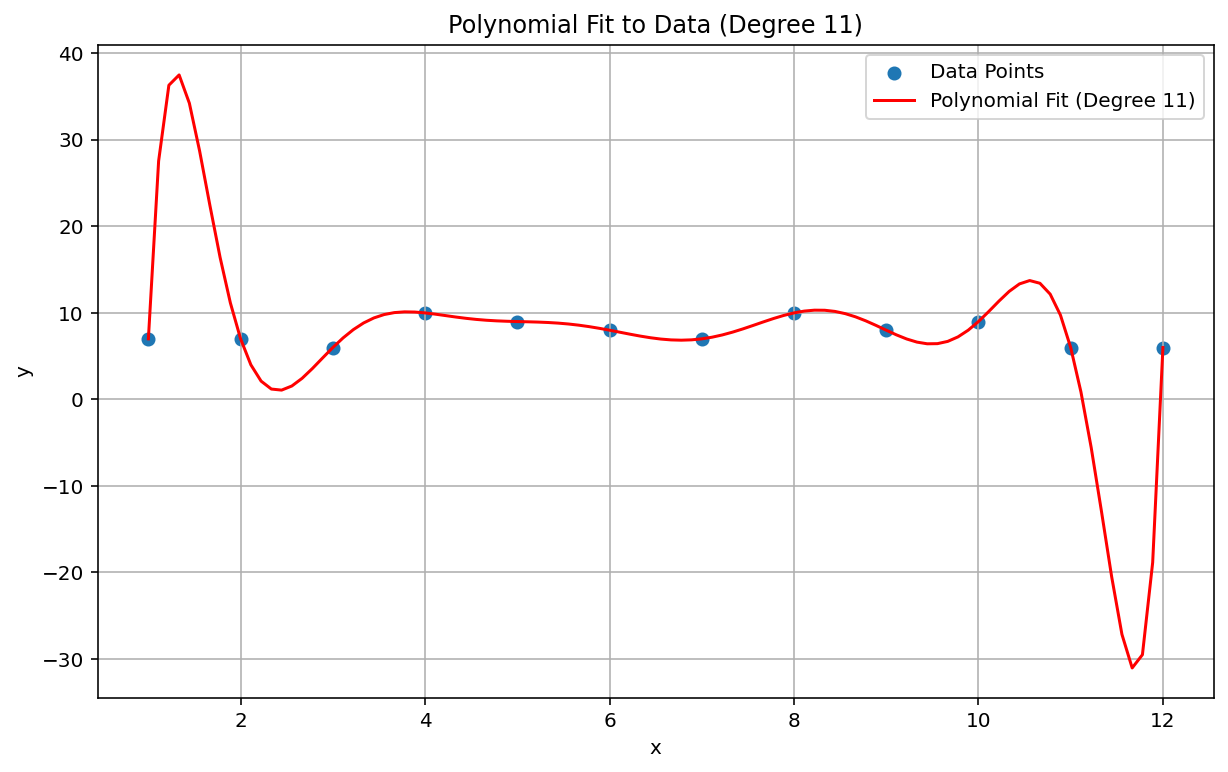
Im Kontext von ML ist das Overfitting ein ähnliches Phänomen.
Statistische Fehlalarme
Manchmal ist ein statistischer Test zu wenig aussagekräftig, um einen kleinen Effekt zu erkennen. Eine geringe Teststatistik bedeutet eine geringe Wahrscheinlichkeit, dass tatsächliche Ereignisse korrekt erkannt werden, und daher eine hohe Wahrscheinlichkeit für falsch negative Ergebnisse. Katherine Button et al. schrieben in Nature: „Wenn Studien in einem bestimmten Bereich mit einer Teststärke von 20 % konzipiert sind, bedeutet das, dass bei 100 echten nicht nullwertigen Effekten, die in diesem Bereich entdeckt werden sollen, mit diesen Studien voraussichtlich nur 20 entdeckt werden.“ Manchmal kann eine größere Stichprobengröße helfen, ebenso wie eine sorgfältige Studienausführung.
Eine analoge Situation in der ML ist das Problem der Klassifizierung und die Auswahl eines Klassifizierungsgrenzwerts. Ein höherer Schwellenwert führt zu weniger falsch positiven und mehr falsch negativen Ergebnissen, während ein niedrigerer Schwellenwert zu mehr falsch positiven und weniger falsch negativen Ergebnissen führt.
Neben Problemen mit der statistischen Potenz kann es vorkommen, dass nicht lineare Korrelationen zwischen Variablen übersehen werden, da Korrelationen lineare Beziehungen erkennen sollen. Ebenso können Variablen miteinander in Beziehung stehen, aber nicht statistisch korreliert sein. Variablen können auch negativ korreliert, aber völlig unabhängig sein. Dies wird als Berkson-Paradoxon oder Berkson-Fehler bezeichnet. Das klassische Beispiel für den Berkson-Fehler ist die irreführende negative Korrelation zwischen einem Risikofaktor und einer schweren Krankheit bei der Betrachtung einer stationären Krankenhauspopulation im Vergleich zur Allgemeinbevölkerung, die sich aus dem Auswahlprozess ergibt (eine Erkrankung, die schwer genug ist, um eine Krankenhauseinweisung zu erfordern).
Überlegen Sie, ob eine dieser Situationen auf Sie zutrifft.
Veraltete Modelle und ungültige Annahmen
Selbst gute Modelle können sich im Laufe der Zeit verschlechtern, da sich das Verhalten (und die Welt) ändern kann. Die ersten Prognosemodelle von Netflix mussten eingestellt werden, da sich der Kundenstamm von jungen, technikaffinen Nutzern auf die Allgemeinbevölkerung verlagerte.10
Modelle können auch stillschweigende und ungenaue Annahmen enthalten, die bis zum katastrophalen Ausfall des Modells verborgen bleiben können, wie beim Börsencrash von 2008. Die Value-at-Risk-Modelle (VaR) der Finanzbranche sollten den maximalen Verlust des Portfolios eines Händlers genau schätzen, z. B. einen maximalen Verlust von 100.000$,der in 99% der Fälle erwartet wird. Unter den abnormalen Bedingungen des Crashs verlor ein Portfolio mit einem erwarteten maximalen Verlust von 100.000$ manchmal 1.000.000$ oder mehr.
Die VaR-Modelle basierten auf falschen Annahmen, darunter:
- Vergangene Marktveränderungen sind ein Indikator für zukünftige Marktveränderungen.
- Die prognostizierten Renditen basierten auf einer normalen (d. h. schmalschwanzigen und daher vorhersehbaren) Verteilung.
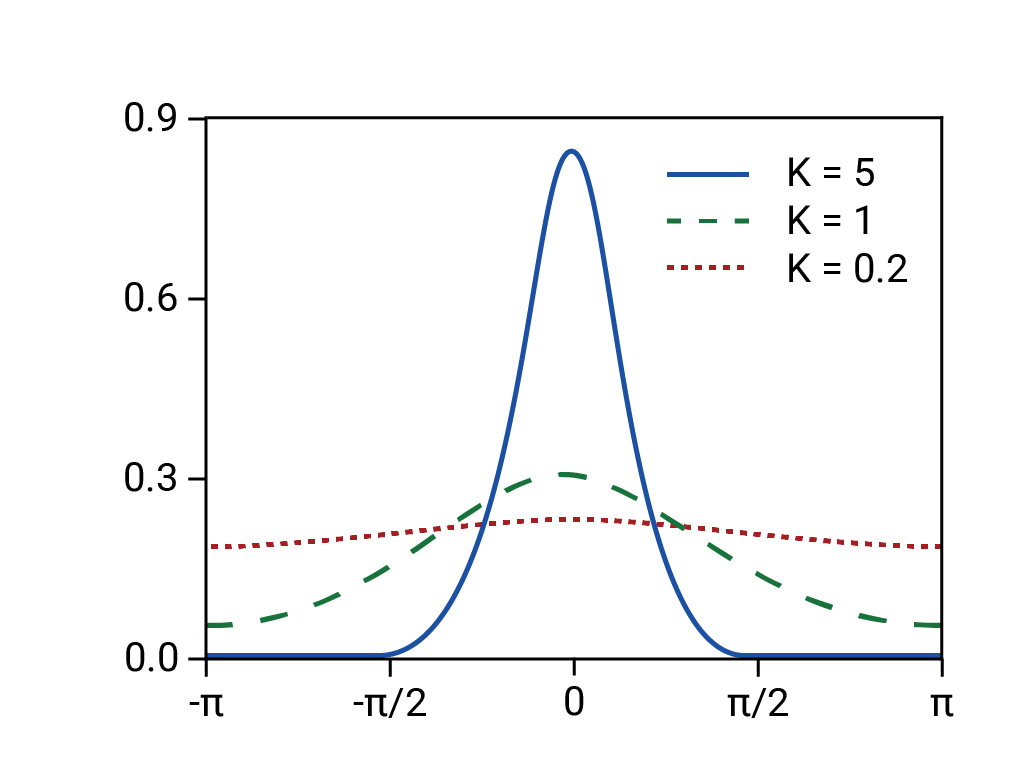
Tatsächlich war die zugrunde liegende Verteilung „fettleibig“, „wild“ oder fraktal, was bedeutet, dass das Risiko für Long-Tail-, extreme und vermeintlich seltene Ereignisse viel höher war, als es bei einer Normalverteilung der Fall wäre. Die Langschwanzigkeit der tatsächlichen Verteilung war zwar bekannt, wurde aber nicht berücksichtigt. Weniger bekannt war, wie komplex und eng verschiedene Phänomene miteinander verbunden waren, einschließlich computergestützten Handels mit automatisierten Verkäufen.11
Probleme bei der Aggregation
Aggregierte Daten, einschließlich der meisten demografischen und epidemiologischen Daten, sind mit bestimmten Fallen behaftet. Das Paradoxon von Simpson oder Verschmelzungsparadoxon tritt bei aggregierten Daten auf, wenn scheinbare Trends verschwinden oder sich umkehren, wenn die Daten auf einer anderen Ebene aggregiert werden. Das liegt an Störfaktoren und falsch verstandenen Kausalbeziehungen.
Der ökologische Fehlschluss besteht darin, dass Informationen zu einer Population auf einer Aggregationsebene fälschlicherweise auf eine andere Aggregationsebene extrapoliert werden, wo die Behauptung möglicherweise nicht gültig ist. Eine Krankheit, die 40% der landwirtschaftlichen Arbeiter in einer Provinz betrifft, ist in der Gesamtbevölkerung möglicherweise nicht in gleichem Maße verbreitet. Es ist auch sehr wahrscheinlich, dass es in dieser Provinz vereinzelte Bauernhöfe oder landwirtschaftliche Städte gibt, in denen die Krankheit nicht so stark verbreitet ist. Es wäre irreführend, auch in diesen weniger betroffenen Gebieten eine Prävalenz von 40% anzunehmen.
Das Modifiable Areal Unit Problem (MAUP) ist ein bekanntes Problem bei georäumlichen Daten, das 1984 von Stan Openshaw in CATMOG 38 beschrieben wurde. Je nach Form und Größe der Gebiete, in denen Daten zusammengefasst werden, kann ein Experte für raumbezogene Daten fast jede Korrelation zwischen Variablen in den Daten herstellen. Die Festlegung von Wahlbezirken, die eine Partei begünstigen, ist ein Beispiel für MAUP.
In allen diesen Fällen kommt es zu einer unangemessenen Extrapolation von einer Aggregationsebene auf eine andere. Für verschiedene Analyseebenen können unterschiedliche Aggregationen oder sogar völlig unterschiedliche Datensätze erforderlich sein.12
Beachten Sie, dass Volkszählungs-, demografische und epidemiologische Daten aus Datenschutzgründen in der Regel nach Zonen zusammengefasst werden. Diese Zonen sind oft willkürlich, d. h., sie basieren nicht auf sinnvollen realen Grenzen. Bei der Arbeit mit diesen Datentypen sollten ML-Experten prüfen, ob sich die Modellleistung und die Vorhersagen je nach Größe und Form der ausgewählten Zonen oder der Aggregationsebene ändern und ob die Modellvorhersagen von einem dieser Aggregationsprobleme betroffen sind.
Verweise
Button, Katharine et al. „Power failure: why small sample size undermines the reliability of neuroscience.“ Nature Reviews Neuroscience, Band 14 (2013), 365–376. DOI: https://doi.org/10.1038/nrn3475
Kairo, Alberto. How Charts Lie: Getting Smarter about Visual Information NY: W.W. Norton, 2019.
Davenport, Thomas H. „A Predictive Analytics Primer“ In HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), S. 81–86.
De Langhe, Bart, Stefano Puntoni und Richard Larrick. „Lineares Denken in einer nichtlinearen Welt“ In HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), S. 131–154.
Ellenberg, Jordan. How Not to Be Wrong: The Power of Mathematical Thinking NY: Penguin, 2014.
Huff, Darrell. How to Lie with Statistics NY: W.W. Norton, 1954.
Jones, Ben. Datenfallen vermeiden Hoboken, NJ: Wiley, 2020.
Openshaw, Stan. „The Modifiable Areal Unit Problem“, CATMOG 38 (Norwich, England: Geo Books 1984) 37.
The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) (testimonies of Nassim N. Taleb und Richard Bookstaber).
Ritter, David. „When to Act on a Correlation, and When Not To“ (Wann Sie auf eine Korrelation reagieren sollten und wann nicht) In HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), S. 103–109.
Tulchinsky, Theodore H. and Elena A. Varavikova. „Kapitel 3: Gesundheit einer Bevölkerung messen, beobachten und bewerten“ in The New Public Health, 3. Auflage, San Diego: Academic Press, 2014, S. 91–147. DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.
Van Doorn, Jenny, Peter C. Verhoef und Tammo H. A. Bijmolt. „Die Bedeutung nichtlinearer Beziehungen zwischen Einstellung und Verhalten in der Politikforschung.“ Journal of Consumer Policy 30 (2007) 75–90. DOI: https://doi.org/10.1007/s10603-007-9028-3
Bildreferenz
Basierend auf der „Von-Mises-Verteilung“. Rainald62, 2018. Quelle
-
Ellenberg 125. ↩
-
Huff 77–79. Huff zitiert das Office of Public Opinion Research der Princeton University, aber er könnte auch an den Bericht vom April 1944 des National Opinion Research Center an der University of Denver gedacht haben. ↩
-
Tulchinsky und Varavikova. ↩
-
Gary Taubes, Do We Really Know What Makes Us Healthy? (Wissen wir wirklich, was uns gesund macht?), The New York Times Magazine, 16. September 2007. ↩
-
Ellenberg 78. ↩
-
Huff 91–92. ↩
-
Huff 93. ↩
-
Jones 157–167. ↩
-
Huff 95. ↩
-
Davenport 84. ↩
-
Siehe die Aussage von Nassim N. vor dem US-Kongress. Taleb und Richard Bookstaber in The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) 11–67. ↩
-
Kairo 155, 162. ↩