"כל המודלים שגויים, אבל חלקם יעילים". – ג'ורג' בוקס (George Box), 1978
למרות שהן יעילות, לטכניקות סטטיסטיות יש מגבלות. הבנת המגבלות האלה יכולה לעזור לחוקרים להימנע מטעויות ומטענות לא מדויקות, כמו ההצהרה של BF Skinner ששייקספיר לא השתמש באליטרציה יותר ממה שאפשר לצפות באופן אקראי. (מחקר Skinner היה חלש.1)
אי ודאות וסרגלי שגיאה
חשוב לציין את אי-הוודאות בניתוח. חשוב באותה מידה למדוד את מידת אי-הוודאות בניתוח של אנשים אחרים. יכול להיות שנקודות נתונים שנראות כמגמה בתרשים, אבל יש להן פסי שגיאה חופפים, לא מציינות דפוס בכלל. יכול להיות גם שרמת אי-הוודאות גבוהה מדי כדי להסיק מסקנות מועילות ממחקרים או מבדיקות סטטיסטיות מסוימים. אם במחקר נדרש דיוק ברמת המגרש, מערך נתונים גיאו-מרחביים עם רמת אי-ודאות של +/- 500 מ' הוא לא מתאים לשימוש.
לחלופין, רמות אי הוודאות יכולות להיות שימושיות בתהליכי קבלת החלטות. נתונים שתומכים בטיפול מסוים במים עם רמת אי-ודאות של 20% בתוצאות עשויים להוביל להמלצה להטמיע את הטיפול הזה במים, תוך מעקב מתמשך אחרי התוכנית כדי לטפל ברמת אי-הודאות הזו.
רשתות נוירונליות בייסיניות יכולות לכמת את אי-הוודאות על ידי חיזוי של הפצות של ערכים במקום ערכים בודדים.
תוכן לא רלוונטי
כפי שצוין בהקדמה, תמיד יש לפחות פער קטן בין הנתונים לבין המציאות. מומחה ML חכם צריך לקבוע אם מערך הנתונים רלוונטי לשאלה שנשאלת.
Huff מתארת מחקר מוקדם של דעת הקהל, שבו נמצא שהתשובות של אמריקאים לבנים לשאלה כמה קל לאפרו-אמריקאים להתפרנס קשורות ישירות ובאופן הפוך לרמת האמפתיה שלהם כלפי אפרו-אמריקאים. ככל שהאיבה הגזעית גברה, התשובות לגבי ההזדמנויות הכלכליות הצפויות הפכו לאופטימיות יותר ויותר. יכול להיות שהדבר הוצג בטעות כסימן להתקדמות. עם זאת, המחקר לא הצליח להראות מהן ההזדמנויות הכלכליות בפועל שזמינות לאפרו-אמריקאים באותה תקופה, והוא לא התאים להסקת מסקנות לגבי המציאות בשוק העבודה – אלא רק לגבי הדעות של המשיבים בסקר. הנתונים שנאספו לא היו רלוונטיים למצב בשוק העבודה.2
אפשר לאמן מודל על נתוני סקרים כמו אלה שמתוארים למעלה, כאשר הפלט למעשה מודד אופטימיזם ולא הזדמנות. עם זאת, מכיוון שהזדמנויות חזויות לא רלוונטיות להזדמנויות אמיתיות, אם תטענו שהמודל חוזה הזדמנויות אמיתיות, תהיה זו מצג שווא של מה שהמודל חוזה.
משתני מבלבלים
משתנה מבלבל, גורם מבלבל או גורם משתנה הוא משתנה שלא נכלל במחקר,שמשפיע על המשתנים שנכללים במחקר ועשוי לגרום לעיוות בתוצאות. לדוגמה, ניקח מודל למידת מכונה שמתבסס על מאפייני מדיניות בריאות הציבור כדי לחזות את שיעורי התמותה במדינה מסוימת. נניח שגיל החציון הוא לא מאפיין. נניח גם שבמדינות מסוימות האוכלוסייה מבוגרת יותר מאשר במדינות אחרות. התעלמות מהמשתנה המבלבל של גיל החציון עלולה לגרום לכך שהמודל יחזה שיעורי תמותה שגויים.
בארצות הברית, לעיתים קרובות יש מתאם חזק בין גזע לבין מעמד סוציו-אקונומי, אבל רק הגזע, ולא המעמד, מתועד בנתוני התמותה. לגורמים מפריעים שקשורים למעמד חברתי, כמו גישה לשירותי בריאות, תזונה, עבודה מסוכנת ודיור מאובטח, עשויה להיות השפעה חזקה יותר על שיעורי התמותה מאשר לגזע, אבל הם לא נכללים במערכי הנתונים.3 זיהוי של הגורמים המפריעים האלה ובקרה עליהם חיוניים ליצירת מודלים שימושיים וליצירת מסקנות משמעותיות ומדויקות.
אם מודל מאומן על נתוני תמותה קיימים, שכוללים את המאפיין 'גזע' אבל לא את המאפיין 'מעמד', הוא עשוי לחזות את התמותה על סמך הגזע, גם אם המעמד הוא מנבא חזק יותר של התמותה. הדבר עלול להוביל להנחות לא מדויקות לגבי קשר סיבתי ולתחזיות לא מדויקות לגבי תמותת חולים. מומחי ה-ML צריכים לבדוק אם יש בנתונים שלהם משתנים מפריעים, וגם אילו משתנים משמעותיים עשויים להיות חסרים במערך הנתונים שלהם.
בשנת 1985, במסגרת המחקר Nurses' Health Study, מחקר עוקב של קבוצה סטטיסטית מבית הספר לרפואה של אוניברסיטת הרווארד ומבית הספר לבריאות הציבור של אוניברסיטת הרווארד, נמצא שנשים בקבוצה הסטטיסטית שלקחו טיפול הורמונלי חלופי עם אסטרוגן סבלו פחות מהתקפי לב בהשוואה לנשים בקבוצה הסטטיסטית שלא נטלו אף פעם אסטרוגן. כתוצאה מכך, רופאים רשמו אסטרוגן למטופלות בגיל המעבר ובגיל הפרסה במשך עשרות שנים, עד שמחקר קליני שנערך בשנת 2002 זיהה סיכוני בריאות שנוצרים כתוצאה מטיפול ארוך טווח באסטרוגן. השימוש באסטרוגן לנשים לאחר גיל המעבר הופסק, אבל לא לפני שגרם לכמה עשרות אלפי מקרי מוות מוקדמים.
יכול להיות שהשיוך נגרם בגלל כמה גורמים מפריעים. אפידמיולוגים מצאו שנשים שמשתמשות בטיפול הורמונלי חלופי, בהשוואה לנשים שלא משתמשות בו, הן בדרך כלל רזות יותר, משכילות יותר, עשירות יותר, מודעות יותר לבריאות שלהן ויש להן סיכוי גבוה יותר לעסוק בפעילות גופנית. במחקרים שונים נמצא שאנשים עם השכלה גבוהה ועם הכנסה גבוהה יותר נמצאים בסיכון נמוך יותר לחלות במחלות לב. ההשפעות האלה היו עלולות לבלבל את הקשר לכאורה בין טיפול באסטרוגן לבין התקפי לב.4
אחוזים עם מספרים שליליים
מומלץ להימנע משימוש באחוזים כשיש מספרים שליליים,5 כי הם עלולים להסתיר כל מיני רווחים והפסדים משמעותיים. לצורך חישוב פשוט, נניח שבענף המסעדות יש 2 מיליון משרות. אם ענף המסעדות יפסיד מיליון משרות כאלה בסוף מרץ 2020, לא יהיה שינוי נטו במשך עשרה חודשים ויחזיר 900,000 משרות בתחילת פברואר 2021, השוואה בין השנים בתחילת מרץ 2021 תצביע על ירידה של 5% בלבד במספר המשרות במסעדות. בהנחה שלא בוצעו שינויים אחרים, השוואה בין נתוני סוף אפריל 2021 לנתוני סוף אפריל 2020 תצביע על עלייה של 90% במספר המשרות במסעדות, וזו תמונה שונה מאוד מהמציאות.
עדיף להשתמש במספרים בפועל, שמותאמים כראוי. מידע נוסף זמין במאמר עבודה עם נתונים מספריים.
שגיאת Post-hoc וקורלציות לא ניתנות לשימוש
השגיאה של 'אחרי-כן ולכן' היא ההנחה שאירוע א' גרם לאירוע ב' כי אירוע א' התרחש לפני אירוע ב'. במילים פשוטות יותר, מדובר בהנחה של קשר סיבה ותוצאה כשאין קשר כזה. באופן פשוט יותר: מתאמים לא מוכיחים סיבתיות.
בנוסף לקשר ברור של סיבה ותוצאה, קורלציות יכולות לנבוע גם מ:
- במקרה טהור (לאיורים, כולל קשר חזק בין שיעור הגירושים במיין לבין צריכת המרגרינה, אפשר לעיין במאמר של Tyler Vigen בנושא Spurious correlations).
- קשר אמיתי בין שני משתנים, אבל עדיין לא ברור איזה משתנה גורם לאיזה משתנה.
- גורם שלישי נפרד שמשפיע על שני המשתנים, למרות שהמשתנים המקוריים לא קשורים זה לזה. לדוגמה, אינפלציה גלובלית יכולה להעלות את המחירים של יאכטות ושל סלרי.6
כמו כן, מסוכן להסיק קורלציה מעבר לנתונים הקיימים. הופ מציין שקצת גשם ישפר את היבול, אבל יותר מדי גשם יזיק לו. הקשר בין הגשם לבין התוצאות של היבול הוא לא לינארי.7 (מידע נוסף על קשרים לא לינאריים זמין בשני הקטעים הבאים). ג'ונס מציין שהעולם מלא באירועים בלתי צפויים, כמו מלחמות ורעב, שגורמים לחוסר ודאות רב בתחזיות העתידיות של נתוני סדרות זמן.8
בנוסף, גם אם יש מתאם אמיתי שמבוסס על קשר סיבתי, יכול להיות שהוא לא יעזור לכם לקבל החלטות. לדוגמה, Huff מציג את המתאם בין התאמה לנישואין להשכלה גבוהה בשנות ה-50. נשים שלמדו במכללה היו פחות נוטה להתחתן, אבל יכול להיות שנשים שלמדו במכללה היו פחות נוטה להתחתן מלכתחילה. אם זה המצב, השכלה אקדמית לא שינתה את הסבירות שלהם להתחתן.9
אם ניתוח מזהה מתאם בין שני משתנים במערך נתונים, כדאי לשאול:
- איזה סוג של מתאם יש: קשר סיבתי, קשר מזויף, קשר לא ידוע או קשר שנגרם על ידי משתנה שלישי?
- מה מידת הסיכון של אקסטרפולציה מהנתונים? כל תחזית של מודל לגבי נתונים שלא נמצאים במערך הנתונים לאימון היא למעשה אינטרפולציה או אקסטרפולציה מהנתונים.
- האם אפשר להשתמש בקורלציה כדי לקבל החלטות מועילות? לדוגמה, יכול להיות שקורלציה חזקה בין אופטימיות לעלייה בשכר, אבל ניתוח סנטימנטים של גוף גדול של נתוני טקסט, כמו פוסטים של משתמשים ברשתות חברתיות במדינה מסוימת, לא יעזור לחזות עליות בשכר במדינה הזו.
כשמאמנים מודל, בדרך כלל מומחי ה-ML מחפשים תכונות שיש להן קורלציה חזקה עם התווית. אם לא מבינים היטב את הקשר בין המאפיינים לבין התווית, זה עלול להוביל לבעיות שמתוארות בקטע הזה, כולל מודלים שמבוססים על מתאם מזויף ומודלים שמניחים שטרנדים היסטוריים ימשיכו בעתיד, כשבפועל הם לא.
ההטיה הליניארית
במאמר Linear Thinking in a Nonlinear World (חשיבה לינארית בעולם לא לינארי), Bart de Langhe, Stefano Puntoni ו-Richard Larrick מתארים את ההטיה הלינארית כנטייה של המוח האנושי לצפות ליחסים לינאריים ולחפש אותם, למרות שרבים מהתופעות הן לא לינאריות. לדוגמה, הקשר בין עמדות אנושיות לבין התנהגות הוא עקומה קמורה ולא קו. במאמר מ-2007 שפורסם ב-Journal of Consumer Policy, שצוטט על ידי de Langhe et al., ג'ני ואן דוורן (Jenny van Doorn) ושותפיה פיתחו מודל של הקשר בין הדאגה של המשיבים בסקר לסביבה לבין הרכישות שלהם של מוצרים אורגניים. אנשים עם דאגה קיצונית ביותר לסביבה קנו יותר מוצרים אורגניים, אבל לא היה הבדל משמעותי בין כל המשיבים האחרים.
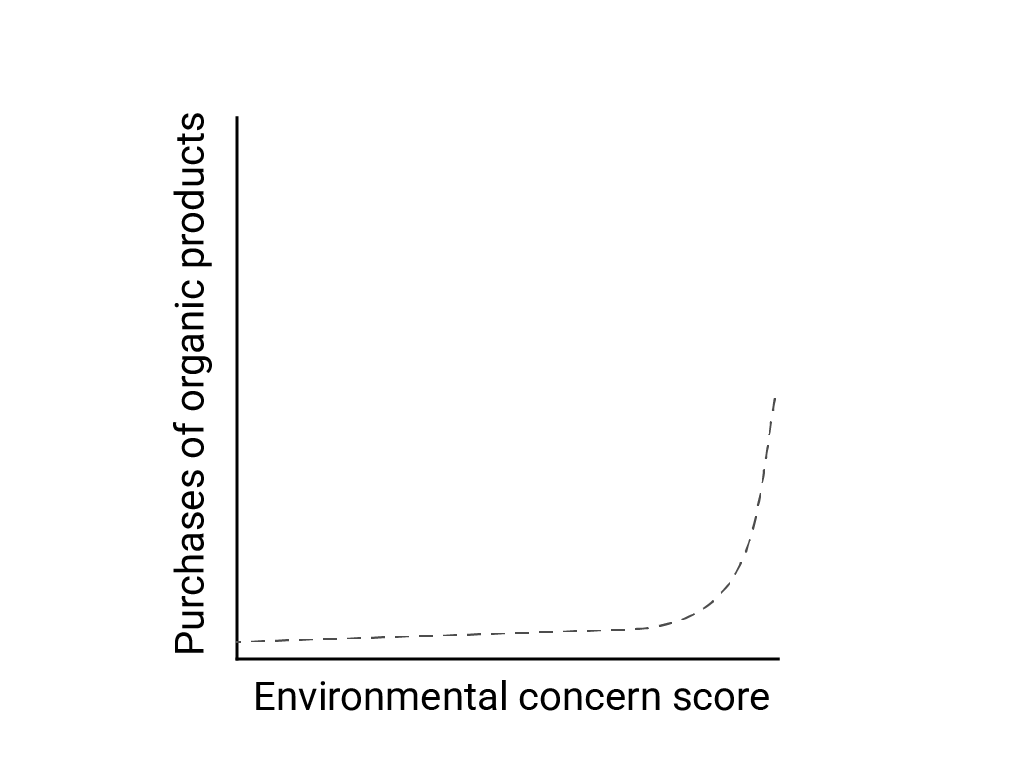
כשאתם מתכננים מודלים או מחקרים, כדאי לקחת בחשבון את האפשרות של יחסי לא לינאריים. מאחר שבדיקות A/B עשויות לפספס קשרים לא לינאריים, מומלץ לבדוק גם תנאי שלישי, ביניים, C. כדאי גם לבדוק אם ההתנהגות הראשונית שנראית ליניארית תמשיך להיות ליניארית, או אם נתונים עתידיים עשויים להראות התנהגות לוגריתמית יותר או התנהגות לא ליניארית אחרת.
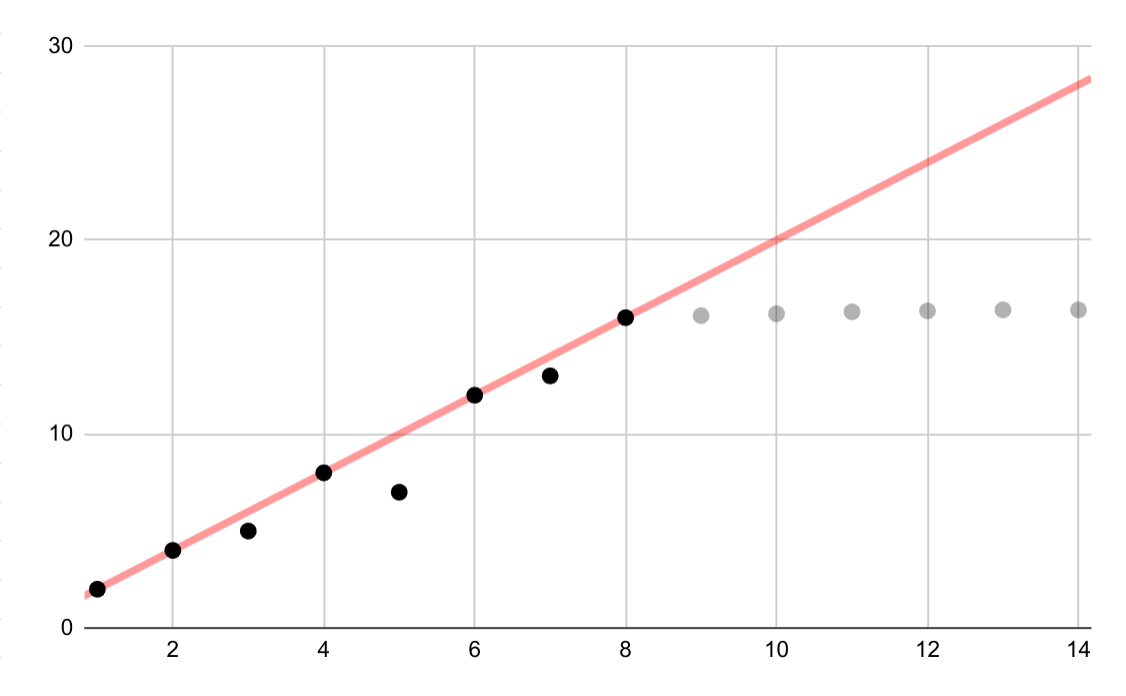
בדוגמה ההיפותטית הזו מוצגת התאמה לינארית שגויה לנתונים לוגריתמיים. אם רק הנקודות הראשונות של הנתונים היו זמינות, יכול להיות שתהיה נטייה להניח קשר לינארי מתמשך בין המשתנים, אבל זו הנחה שגויה.
אינטרפולציה לינארית
בודקים את כל האינטרפולציות בין נקודות הנתונים, כי אינטרפולציה מוסיפה נקודות בדיוניות, והמרווחים בין המדידות האמיתיות עשויים להכיל תנודות משמעותיות. לדוגמה, תוכלו להיעזר בתצוגה החזותית הבאה של ארבע נקודות נתונים שמחוברות באמצעות אינטרפולציות לינאריות:

לאחר מכן, נבחן את הדוגמה הבאה של תנודות בין נקודות נתונים שנמחקות על ידי אינטרפולציה לינארית:
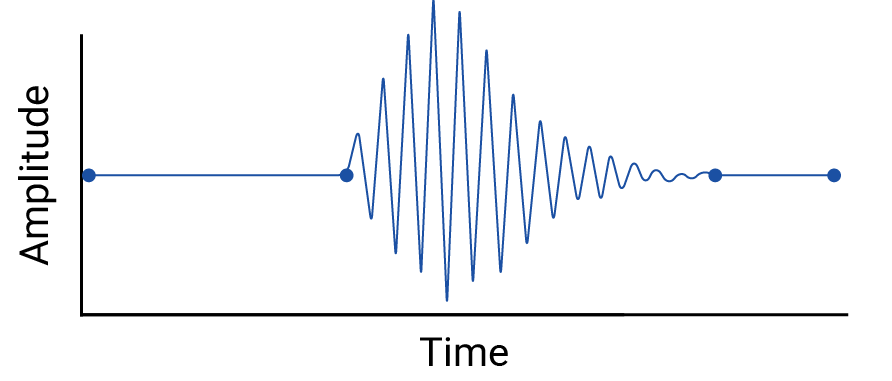
הדוגמה הזו מלאכותית כי סיסמוגרפים אוספים נתונים באופן רציף, ולכן רעידת האדמה הזו לא תחמוק מהם. עם זאת, הוא מועיל להמחשת ההנחות שמבוססות על אינטרפולציות, והתופעות האמיתיות שיכול להיות שמומחים לנתונים יפספסו.
תופעת Runge
תופעת Runge, שנקראת גם 'תנודות פולינומיות', היא בעיה שנמצאת בקצה השני של הספקטרום מבין אינטרפולציה לינארית ושיוך לינארי. כשמתאימים אינטרפולציה פולינומית לנתונים, אפשר להשתמש בפולינום עם דרגה גבוהה מדי (הדרגה, או הסדר, היא החזקה הגבוהה ביותר במשוואת הפולינום). כתוצאה מכך, נוצרים תנודות מוזרות בקצוות. לדוגמה, החלת אינטרפולציה פולינומית של דרגה 11, כלומר שהמונח בעל הדרגה הגבוהה ביותר במשוואה הפולינומית הוא \(x^{11}\), על נתונים לינאריים באופן גס, גורמת לחיזויים גרועים במיוחד בתחילת טווח הנתונים ובסופו:
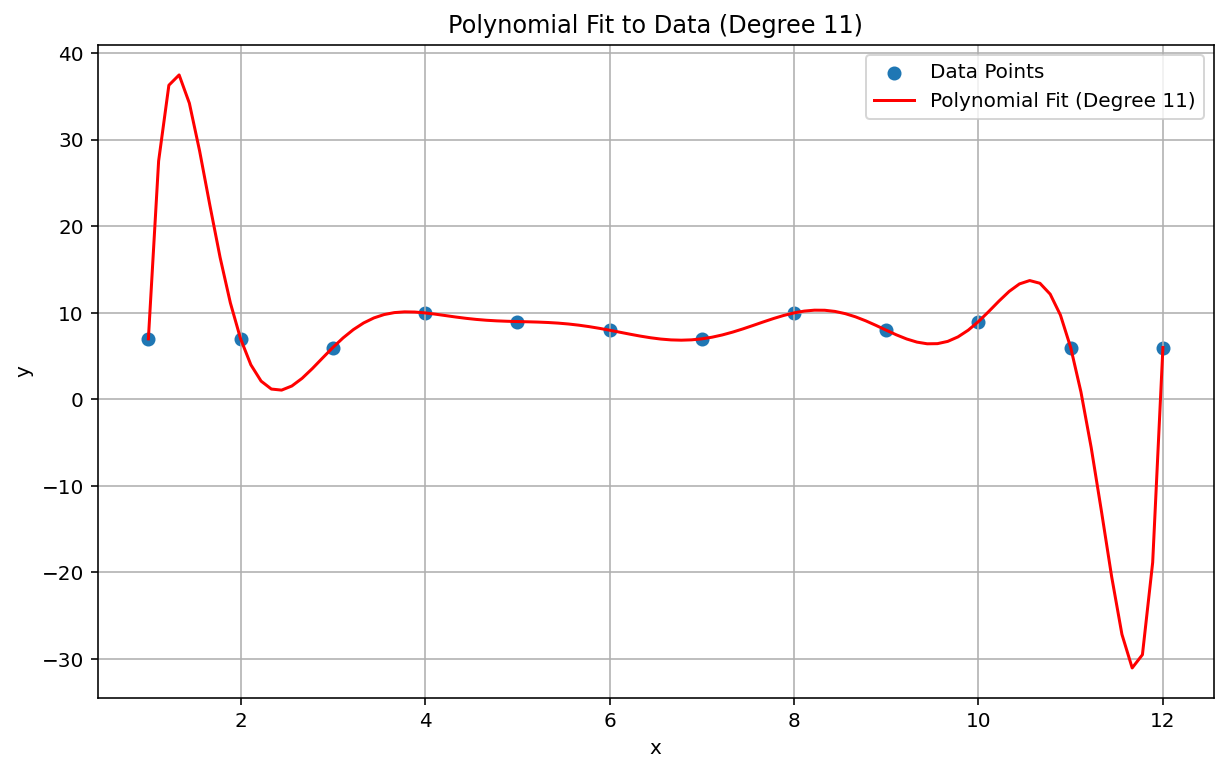
בהקשר של למידת מכונה, תופעה דומה היא התאמה יתר.
כשלים סטטיסטיים בזיהוי
לפעמים בדיקה סטטיסטית חלשה מדי כדי לזהות השפעה קטנה. עוצמה נמוכה בניתוח סטטיסטי פירושה סיכוי נמוך לזהות אירועים אמיתיים בצורה נכונה, ולכן סיכוי גבוה לקבלת תוצאות שליליות שגויות. קתרין באטון (Katherine Button) ושותפיה כתבו ב-Nature: "כשמחקרים בתחום נתון תוכננו עם עוצמה של 20%, המשמעות היא שאם יש 100 השפעות אמיתיות שאינן null שאפשר לגלות בתחום הזה, המחקר צפוי לגלות רק 20 מהן". לפעמים אפשר להגדיל את גודל המדגם, וגם לתכנן את המחקר בצורה יסודית.
מצב דומה בלמידת מכונה הוא בעיית הסיווג ובחירת סף הסיווג. בחירה בסף גבוה יותר מובילה לפחות תוצאות חיוביות שגויות וליותר תוצאות שליליות שגויות, בעוד שבחירה בסף נמוך יותר מובילה ליותר תוצאות חיוביות שגויות ולפחות תוצאות שליליות שגויות.
בנוסף לבעיות שקשורות לעוצמה הסטטיסטית, מאחר שהקורלציה נועדה לזהות קשרים לינאריים, יכול להיות שלא יתגלו קורלציות לא לינאריות בין משתנים. באופן דומה, משתנים יכולים להיות קשורים זה לזה אבל לא להיות בקורלציה סטטיסטית. יכול להיות גם שמשתנים יהיו בקורלציה שלילית אבל לא יהיו קשורים כלל, במה שנקרא פרדוקס Berkson או הטעות של Berkson. הדוגמה הקלאסית לתרמית של Berkson היא הקורלציה השלילית המזויפת בין כל גורם סיכון למחלה חמורה כשבודקים את האוכלוסייה של המאושפזים בבית החולים (בהשוואה לאוכלוסייה הכללית), שנובעת מתהליך הבחירה (מצב חמור מספיק כדי לחייב אשפוז).
כדאי לבדוק אם אחד מהמצבים האלה רלוונטי.
מודלים מיושנים והנחות לא תקינות
גם מודלים טובים יכולים להידרדר עם הזמן כי ההתנהגות (וגם העולם, באותו הנושא) עשויה להשתנות. המודלים החזויים המוקדמים של Netflix הוצאו משימוש כי בסיס הלקוחות שלהם השתנה ממשתמשים צעירים ומנוסים בטכנולוגיה לאוכלוסייה הכללית.10
מודלים יכולים גם להכיל הנחות לא מדויקות ושקטות, שעשויות להישאר מוסתרות עד לכשל קטסטרופלי של המודל, כמו קריסת השוק ב-2008. לפי המודלים של Value at Risk (VaR) בתעשייה הפיננסית, אפשר להעריך במדויק את ההפסד המקסימלי שצפוי ב-99% מהמקרים בתיק ההשקעות של כל סוחר, למשל הפסד מקסימלי של $100,000. אבל בתנאים החריגים של המשבר, לפעמים הפסד של תיק השקעות עם אומדן הפסד מקסימלי של $100,000 הגיע ל-$1,000,000 או יותר.
מודלים של VaR התבססו על הנחות שגויות, כולל:
- שינויים קודמים בשוק יכולים לחזות שינויים עתידיים בשוק.
- ההחזרים הצפויים התבססו על התפלגות נורמלית (עם זנב דק, ולכן צפויה).
למעשה, ההתפלגות הבסיסית הייתה 'פראית', עם 'זנב ארוך' או פרקטלית, כלומר היה סיכון גבוה בהרבה לאירועים ארוכי-זנב, קיצוניים ונדירים לכאורה, בהשוואה לסיכון שצפוי בהתפלגות רגילה. היה ידוע שההתפלגות האמיתית היא עם זנב ארוך, אבל לא ננקטו פעולות בהתאם. מה שלא היה ידוע באותה תקופה הוא עד כמה התופעות השונות מורכבות ומקושרות זו לזו, כולל מסחר מבוסס-מחשב עם מכירות אוטומטיות.11
בעיות שקשורות לצבירת נתונים
נתונים שמצטברים, כולל רוב הנתונים הדמוגרפיים והאפידמיולוגיים, כפופים לקבוצה מסוימת של מלכודות. הפרדוקס של סימפסון, או הפרדוקס של המיזוג, מתרחש בנתונים מצטברים שבהם מגמות לכאורה נעלמות או משתנות כשהנתונים נצברים ברמה אחרת, בגלל גורמים מבלבלים ויחסי סיבה-תוצאה שגויים.
השגיאה האקולוגית היא שגיאה שמתרחשת כשמפיצים בטעות מידע על אוכלוסייה ברמת צבירת אחת לרמת צבירת אחרת, שבו ייתכן שהטענה לא תקפה. יכול להיות שמחלה שמשפיעה על 40% מעובדי החקלאות במחוז אחד לא תהיה נפוצה באותה מידה באוכלוסייה הרחבה יותר. בנוסף, סביר מאוד שיהיו חוות או עיירות חקלאיות מבודדות באותה פרובינציה שבהן לא תהיה שכיחות גבוהה דומה של המחלה. יהיה שגוי להניח שגם במקומות שהושפעו פחות יש שכיחות של 40%.
הבעיה של יחידת שטח שניתן לשינוי (MAUP) היא בעיה ידועה בנתונים גיאו-מרחביים, שתיאר סטן אופנשו (Stan Openshaw) בשנת 1984 במאמר ב-CATMOG 38. בהתאם לצורות ולגדלים של האזורים שבהם נעשה שימוש כדי לצבור נתונים, מומחה לנתונים גיאו-מרחביים יכול לזהות כמעט כל קורלציה בין המשתנים בנתונים. דוגמה לשימוש ב-MAUP היא יצירת מחוזות בחירה שמעדיפים מפלגה מסוימת.
כל המצבים האלה כוללים אקסטרפולציה לא הולמת מרמת צבירת נתונים אחת לרמה אחרת. רמות ניתוח שונות עשויות לדרוש צבירות שונות או אפילו מערכי נתונים שונים לגמרי.12
חשוב לזכור שנתוני מפקד האוכלוסין, הנתונים הדמוגרפיים והנתונים האפידמיולוגיים נצברים בדרך כלל לפי תחומים, מטעמי פרטיות. בנוסף, התחומים האלה הם לרוב שרירותיים, כלומר הם לא מבוססים על גבולות משמעותיים בעולם האמיתי. כשעובדים עם סוגי הנתונים האלה, מומחי ה-ML צריכים לבדוק אם הביצועים והתחזיות של המודל משתנים בהתאם לגודל ולצורה של האזורים שנבחרו או לרמת הסיכום, ואם כן, אם אחת מבעיות הסיכום האלה משפיעה על התחזיות של המודל.
קובצי עזר
Button, Katharine et al. "Power failure: why small sample size undermines the reliability of neuroscience" Nature Reviews Neuroscience, כרך 14 (2013), 365-376. DOI: https://doi.org/10.1038/nrn3475
Cairo, Alberto. How Charts Lie: Getting Smarter about Visual Information ניו יורק: W.W. Norton, 2019.
Davenport, Thomas H. "A Predictive Analytics Primer" HBR Guide to Data Analytics Basics for Managers (בוסטון: HBR Press, 2018), עמ' 81-86.
De Langhe, Bart, Stefano Puntoni ו-Richard Larrick. "חשיבה לינארית בעולם לא לינארי" HBR Guide to Data Analytics Basics for Managers (בוסטון: HBR Press, 2018), עמ' 131-154.
Ellenberg, ירדן. How Not to Be Wrong: The Power of Mathematical Thinking ניו יורק: Penguin, 2014.
Huff, Darrell. איך משקרים באמצעות נתונים סטטיסטיים ניו יורק: W.W. Norton, 1954.
ג'ונס, בן. הימנעות ממלכודות שקשורות לנתונים Hoboken, NJ: Wiley, 2020.
Openshaw, Stan. "The Modifiable Areal Unit Problem", CATMOG 38 (Norwich, England: Geo Books 1984) 37.
The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) (testimonies of Nassim N. Taleb וריצ'רד בוקסטאבר).
Ritter, David. "מתי כדאי לפעול על סמך מתאם ומתי לא כדאי" HBR Guide to Data Analytics Basics for Managers (בוסטון: HBR Press, 2018), עמ' 103-109.
Tulchinsky, Theodore H. and Elena A. Varavikova. "פרק 3: מדידה, מעקב והערכה של בריאות האוכלוסייה" בספר The New Public Health (הדור החדש של בריאות הציבור), מהדורה שלישית. סן דייגו: Academic Press, 2014, עמ' 91-147. DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.
Van Doorn, Jenny, Peter C. Verhoef, ו-Tammo H. תשובה: Bijmolt. "The importance of relationships non-linear between attitude and behaviour in policy research" Journal of Consumer Policy 30 (2007) 75–90. DOI: https://doi.org/10.1007/s10603-007-9028-3
תמונה להמחשה
על סמך 'התפלגות Von Mises'. Rainald62, 2018. מקור
-
Ellenberg 125. ↩
-
Huff 77-79. הופ מצטט את המשרד לחקר דעת קהל של פרינסטון, אבל יכול להיות שהוא התכוון לדוח מחודש אפריל 1944 של המרכז הלאומי לחקר דעת קהל באוניברסיטת דנוור. ↩
-
Tulchinsky ו-Varavikova. ↩
-
גארי טאובס (Gary Taubes), Do We Really Know What Makes Us Healthy? (האם אנחנו באמת יודעים מה עושה אותנו בריאים?), The New York Times Magazine, 16 בספטמבר 2007. ↩
-
Ellenberg 78. ↩
-
Huff 91-92. ↩
-
Huff 93. ↩
-
Jones 157-167. ↩
-
Huff 95. ↩
-
Davenport 84. ↩
-
עדותו של Nassim N. בפני הקונגרס Taleb ו-Richard Bookstaber במאמר The Risks of Financial Modeling: VaR and the Economic Meltdown, הקונגרס ה-111 (2009) 11-67. ↩
-
קהיר 155, 162. ↩