Vì quá trình tạo cụm không có giám sát, nên không có thông tin thực tế nào để xác minh kết quả. Việc thiếu sự thật khiến việc đánh giá chất lượng trở nên phức tạp. Hơn nữa, các tập dữ liệu thực tế thường không cung cấp các cụm ví dụ rõ ràng như trong ví dụ minh hoạ trong Hình 1.
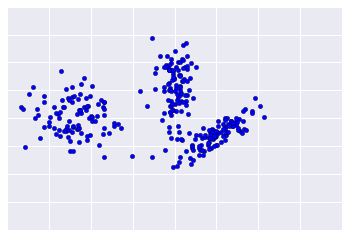
Thay vào đó, dữ liệu thực tế thường giống như Hình 2, khiến bạn khó có thể đánh giá chất lượng cụm theo cách trực quan.
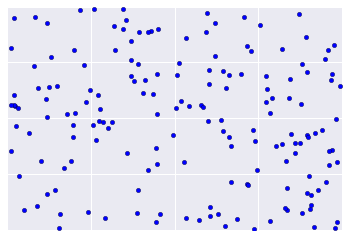
Tuy nhiên, có một số phương pháp phỏng đoán và phương pháp hay nhất mà bạn có thể áp dụng lặp lại để cải thiện chất lượng của quá trình tạo cụm. Biểu đồ quy trình sau đây cung cấp thông tin tổng quan về cách đánh giá kết quả phân cụm. Chúng ta sẽ tìm hiểu chi tiết về từng bước.

Bước 1: Đánh giá chất lượng của quá trình tạo cụm
Trước tiên, hãy kiểm tra để đảm bảo các cụm trông như bạn mong đợi và các ví dụ mà bạn coi là tương tự nhau xuất hiện trong cùng một cụm.
Sau đó, hãy kiểm tra những chỉ số thường dùng sau đây (không phải danh sách đầy đủ):
- Số lượng giá trị riêng biệt của cụm
- Magnitude của cụm
- Hiệu suất hạ nguồn
Số lượng giá trị riêng biệt của cụm
Số lượng giá trị riêng biệt của cụm là số lượng ví dụ trên mỗi cụm. Lập biểu đồ số lượng giá trị riêng biệt của cụm cho tất cả các cụm và điều tra các cụm là các giá trị ngoại lai chính. Trong Hình 2, đây sẽ là cụm 5.
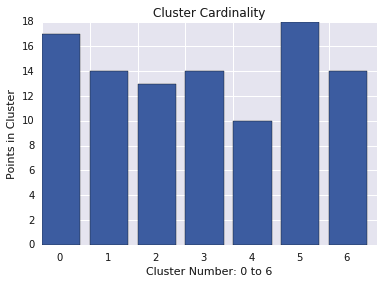
Magnitude của cụm
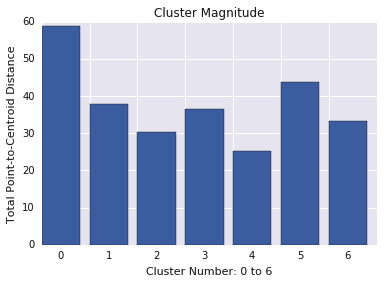
Magnitude of cluster (Magnitude of cluster) là tổng khoảng cách từ tất cả các ví dụ trong một cụm đến tâm của cụm. Vẽ cường độ cụm cho tất cả cụm và điều tra các giá trị ngoại lai. Trong Hình 3, cụm 0 là một giá trị ngoại lai.
Ngoài ra, hãy cân nhắc xem xét khoảng cách tối đa hoặc trung bình của các ví dụ từ tâm điểm, theo cụm, để tìm các giá trị ngoại lai.
Độ lớn so với số lượng giá trị riêng biệt
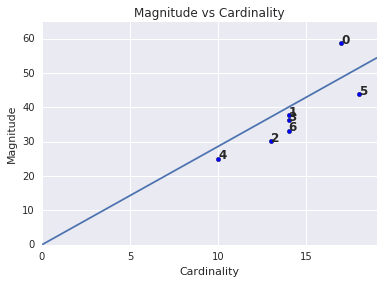
Bạn có thể nhận thấy rằng số lượng giá trị riêng biệt của cụm càng cao thì cường độ của cụm càng cao. Điều này rất dễ hiểu vì càng có nhiều điểm trong một cụm (số lượng giá trị riêng biệt), thì tổng khoảng cách có thể có của các điểm đó từ tâm điểm (cường độ) càng lớn. Bạn cũng có thể xác định các cụm bất thường bằng cách tìm những cụm có mối quan hệ này giữa số lượng giá trị riêng biệt và độ lớn rất khác so với các cụm khác. Trong Hình 4, việc điều chỉnh một đường thẳng cho phù hợp với đồ thị về số lượng giá trị riêng biệt và độ lớn cho thấy cụm 0 là bất thường. (Nhóm 5 cũng cách xa đường thẳng, nhưng nếu bỏ qua nhóm 0, thì đường thẳng vừa vặn mới sẽ gần với nhóm 5 hơn nhiều.)
Hiệu suất hạ nguồn
Vì đầu ra của quá trình phân cụm thường được sử dụng trong các hệ thống học máy hạ nguồn, hãy xem liệu hiệu suất của mô hình hạ nguồn có cải thiện khi quá trình phân cụm của bạn thay đổi hay không. Phương pháp này cung cấp thông tin đánh giá thực tế về chất lượng của kết quả phân cụm, mặc dù việc tiến hành loại kiểm thử này có thể phức tạp và tốn kém.
Bước 2: Đánh giá lại chỉ số tương đồng
Thuật toán phân cụm của bạn chỉ hiệu quả khi có chỉ số đo lường mức độ tương đồng. Đảm bảo rằng phương pháp đo lường mức độ tương đồng của bạn trả về kết quả hợp lý. Bạn có thể kiểm tra nhanh bằng cách xác định các cặp ví dụ được biết là tương tự nhau. Tính toán giá trị đo lường mức độ tương đồng cho mỗi cặp ví dụ và so sánh kết quả với kiến thức của bạn: các cặp ví dụ tương tự nhau sẽ có giá trị đo lường mức độ tương đồng cao hơn so với các cặp ví dụ không tương tự nhau.
Các ví dụ mà bạn sử dụng để kiểm tra nhanh chỉ số tương đồng phải đại diện cho tập dữ liệu, nhờ đó, bạn có thể tự tin rằng chỉ số tương đồng của mình áp dụng cho tất cả các ví dụ. Hiệu suất của biện pháp đo lường mức độ tương đồng, dù là thủ công hay có giám sát, phải nhất quán trên tập dữ liệu. Nếu chỉ số tương đồng của bạn không nhất quán đối với một số ví dụ, thì các ví dụ đó sẽ không được nhóm với các ví dụ tương tự.
Nếu bạn thấy các ví dụ có điểm tương đồng không chính xác, thì có thể là chỉ số tương đồng của bạn chưa thu thập đầy đủ dữ liệu về đặc điểm giúp phân biệt các ví dụ đó. Thử nghiệm với chỉ số tương đồng cho đến khi chỉ số này trả về kết quả chính xác và nhất quán hơn.
Bước 3: Tìm số lượng cụm tối ưu
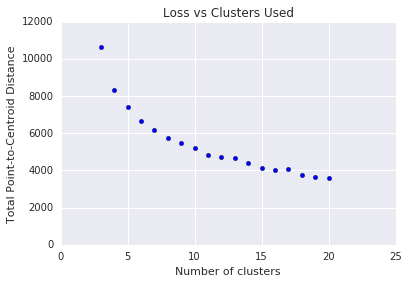
Phương pháp k-means yêu cầu bạn phải quyết định số lượng cụm \(k\) trước. Làm cách nào để xác định \(k\)tối ưu? Hãy thử chạy thuật toán với các giá trị tăng dần của \(k\) và ghi lại tổng của tất cả các cường độ cụm. Khi\(k\) tăng lên, các cụm sẽ nhỏ hơn và tổng khoảng cách của các điểm từ tâm cụm sẽ giảm. Chúng ta có thể coi tổng quãng đường này là tổn thất. Vẽ khoảng cách này so với số lượng cụm.
Như minh hoạ trong Hình 5, ở một \(k\)nhất định, mức giảm tổn thất sẽ trở nên không đáng kể khi \(k\)tăng lên. Cân nhắc sử dụng \(k\) trong đó độ dốc đầu tiên có sự thay đổi đáng kể, được gọi là phương pháp khuỷu tay. Đối với biểu đồ được hiển thị, \(k\) tối ưu là khoảng 11. Nếu muốn các cụm chi tiết hơn, bạn có thể chọn một \(k\)cao hơn bằng cách tham khảo biểu đồ này.
Câu hỏi về cách khắc phục sự cố
Nếu bạn phát hiện vấn đề trong quá trình đánh giá, hãy đánh giá lại các bước chuẩn bị dữ liệu và phương pháp đo lường mức độ tương đồng mà bạn đã chọn. Trả lời câu hỏi:
- Dữ liệu của bạn có được điều chỉnh theo tỷ lệ phù hợp không?
- Chỉ số tương đồng của bạn có chính xác không?
- Thuật toán của bạn có thực hiện các thao tác có ý nghĩa ngữ nghĩa trên dữ liệu không?
- Giả định của thuật toán có khớp với dữ liệu không?
