Étant donné que le clustering est supervisé, aucune vérité terrain n'est disponible pour vérifier les résultats. L'absence de vérité complique l'évaluation de la qualité. De plus, les ensembles de données du monde réel n'offrent généralement pas de groupes d'exemples évidents, comme dans l'exemple illustré à la figure 1.
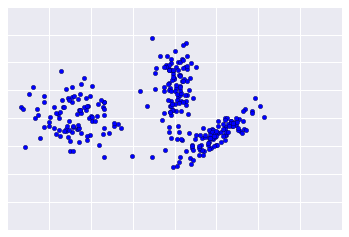
En revanche, les données réelles ressemblent souvent plus à la figure 2, ce qui rend difficile l'évaluation visuelle de la qualité du clustering.
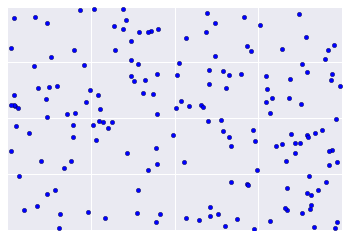
Toutefois, il existe des heuristiques et des bonnes pratiques que vous pouvez appliquer de manière itérée pour améliorer la qualité de votre clustering. L'organigramme suivant présente une vue d'ensemble de l'évaluation des résultats de votre clustering. Nous allons développer chaque étape.

Étape 1: Évaluer la qualité du clustering
Vérifiez d'abord que les clusters correspondent à vos attentes et que les exemples que vous considérez comme similaires apparaissent dans le même cluster.
Consultez ensuite ces métriques couramment utilisées (liste non exhaustive):
- Cardinalité du cluster
- Magnitude du cluster
- Performances en aval
Cardinalité du cluster
La cardinalité du cluster correspond au nombre d'exemples par cluster. Représentez la cardinalité des clusters pour tous les clusters et examinez les clusters qui sont des valeurs aberrantes majeures. Dans la figure 2, il s'agit du cluster 5.
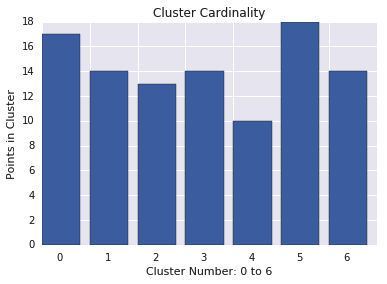
Magnitude du cluster
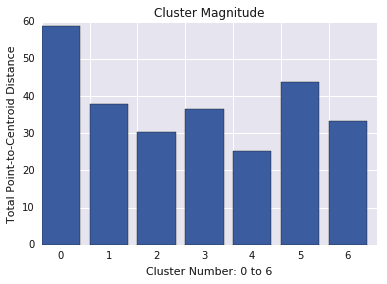
La magnitude du cluster correspond à la somme des distances de tous les exemples d'un cluster au centroïde du cluster. Représentez la magnitude des clusters pour tous les clusters et examinez les valeurs aberrantes. Dans la figure 3, le cluster 0 est une anomalie.
Pensez également à examiner la distance maximale ou moyenne des exemples par rapport aux centroïdes, par cluster, pour trouver des valeurs aberrantes.
Magnitude par rapport à la cardinalité
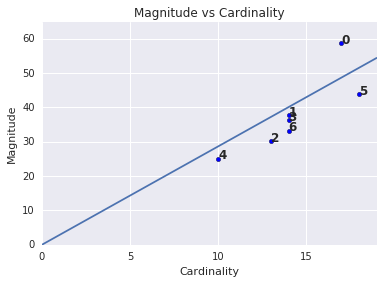
Vous avez peut-être remarqué qu'une cardinalité de cluster plus élevée correspond à une magnitude de cluster plus élevée. Cela semble logique, car plus il y a de points dans un cluster (cardinalité), plus la somme probable des distances de ces points par rapport au centroid (magnitude) est élevée. Vous pouvez également identifier des clusters anormaux en recherchant ceux pour lesquels cette relation entre la cardinalité et l'ampleur est très différente de celle des autres clusters. Dans la figure 4, l'ajustement d'une ligne au graphique de la cardinalité et de la magnitude suggère que le cluster 0 est anormal. (Le cluster 5 est également éloigné de la ligne, mais si le cluster 0 était omis, la nouvelle ligne ajustée serait beaucoup plus proche du cluster 5.)
Performances en aval
Étant donné que les sorties de clustering sont souvent utilisées dans les systèmes de ML en aval, vérifiez si les performances du modèle en aval s'améliorent lorsque votre processus de clustering change. Cela offre une évaluation réelle de la qualité de vos résultats de clustering, bien que ce type de test puisse être complexe et coûteux.
Étape 2: Réévaluer votre mesure de similarité
La qualité de votre algorithme de clustering dépend de votre mesure de similarité. Assurez-vous que votre mesure de similarité renvoie des résultats pertinents. Une vérification rapide consiste à identifier des paires d'exemples connus pour être plus ou moins similaires. Calculez la mesure de similarité pour chaque paire d'exemples, puis comparez vos résultats à vos connaissances: les paires d'exemples similaires doivent avoir une mesure de similarité plus élevée que les paires d'exemples dissemblables.
Les exemples que vous utilisez pour vérifier votre mesure de similarité doivent être représentatifs de l'ensemble de données. Vous pouvez ainsi être sûr que votre mesure de similarité s'applique à tous vos exemples. Les performances de votre mesure de similarité, qu'elle soit manuelle ou supervisée, doivent être cohérentes dans l'ensemble de vos données. Si votre mesure de similarité est incohérente pour certains exemples, ceux-ci ne seront pas regroupés avec des exemples similaires.
Si vous trouvez des exemples avec des scores de similarité inexacts, votre mesure de similarité ne capture probablement pas complètement les données de fonctionnalités qui distinguent ces exemples. Testez votre mesure de similarité jusqu'à ce qu'elle renvoie des résultats plus précis et cohérents.
Étape 3: Déterminer le nombre optimal de clusters
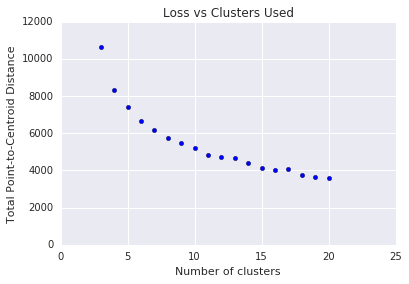
Le clustering en k-moyennes nécessite que vous décidiez du nombre de clusters \(k\) à l'avance. Comment déterminer une \(k\)optimale ? Essayez d'exécuter l'algorithme avec des valeurs croissantes de \(k\) et notez la somme de toutes les magnitudes de cluster. À mesure que\(k\) augmente, les clusters deviennent plus petits et la distance totale des points par rapport aux centroïdes diminue. Nous pouvons considérer cette distance totale comme une perte. Représentez cette distance en fonction du nombre de clusters.
Comme illustré dans la figure 5, au-delà d'une certaine valeur de \(k\), la réduction de la perte devient marginale à mesure que \(k\)augmente. Envisagez d'utiliser la \(k\)à l'endroit où la pente subit un changement radical, ce qui s'appelle la méthode du coude. Pour le graphique affiché, la valeur optimale de \(k\) est d'environ 11. Si vous préférez des clusters plus précis, vous pouvez choisir une valeur \(k\)plus élevée en consultant ce graphique.
Questions de dépannage
Si vous découvrez des problèmes au cours de votre évaluation, réexaminez les étapes de préparation des données et la mesure de similarité choisie. Question :
- Vos données sont-elles mises à l'échelle de manière appropriée ?
- Votre mesure de similarité est-elle correcte ?
- Votre algorithme effectue-t-il des opérations sémantiquement pertinentes sur les données ?
- Les hypothèses de votre algorithme correspondent-elles aux données ?
