В этом разделе рассматриваются этапы подготовки данных, наиболее важные для кластеризации, из модуля «Работа с числовыми данными» ускоренного курса машинного обучения.
При кластеризации вы рассчитываете сходство между двумя примерами, объединяя все данные объектов для этих примеров в числовое значение. Для этого необходимо, чтобы объекты имели одинаковый масштаб, чего можно добиться путем нормализации, преобразования или создания квантилей. Если вы хотите преобразовать данные, не проверяя их распределение, вы можете по умолчанию использовать квантили.
Нормализация данных
Вы можете преобразовать данные для нескольких объектов в один и тот же масштаб, нормализовав данные.
Z-оценки
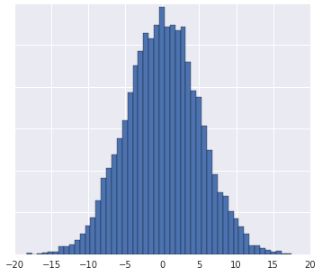
Всякий раз, когда вы видите набор данных, примерно имеющий форму распределения Гаусса , вам следует рассчитать z-показатели для данных. Z-показатели — это количество стандартных отклонений значения от среднего значения. Вы также можете использовать z-показатели, если набор данных недостаточно велик для квантилей.
См. «Масштабирование Z-оценки» , чтобы просмотреть шаги.
Вот визуализация двух особенностей набора данных до и после масштабирования z-показателя:
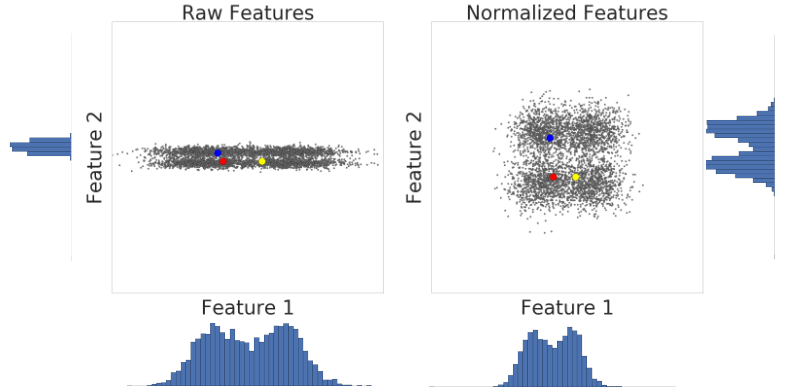
В ненормализованном наборе данных слева Объект 1 и Объект 2, изображенные на графиках по осям X и Y соответственно, не имеют одинакового масштаба. Слева красный пример ближе или более похож на синий, чем на желтый. Справа, после масштабирования z-показателя, функция 1 и функция 2 имеют одинаковый масштаб, а красный пример выглядит ближе к желтому примеру. Нормализованный набор данных дает более точную меру сходства между точками.
Преобразования журналов
Если набор данных идеально соответствует распределению по степенному закону , где данные сильно сгруппированы при самых низких значениях, используйте логарифмическое преобразование. См. Масштабирование журнала , чтобы просмотреть шаги.
Вот визуализация набора степенных данных до и после логарифмического преобразования:
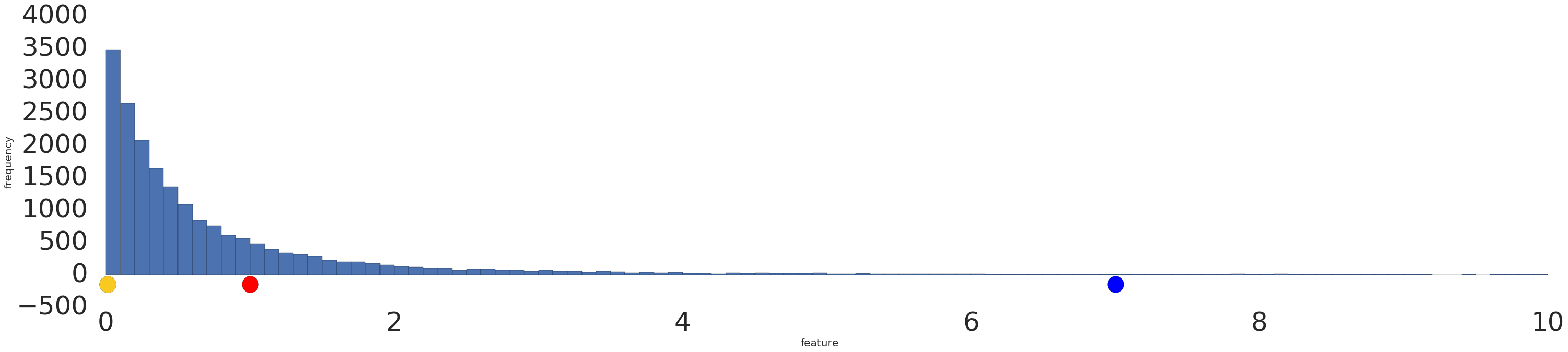
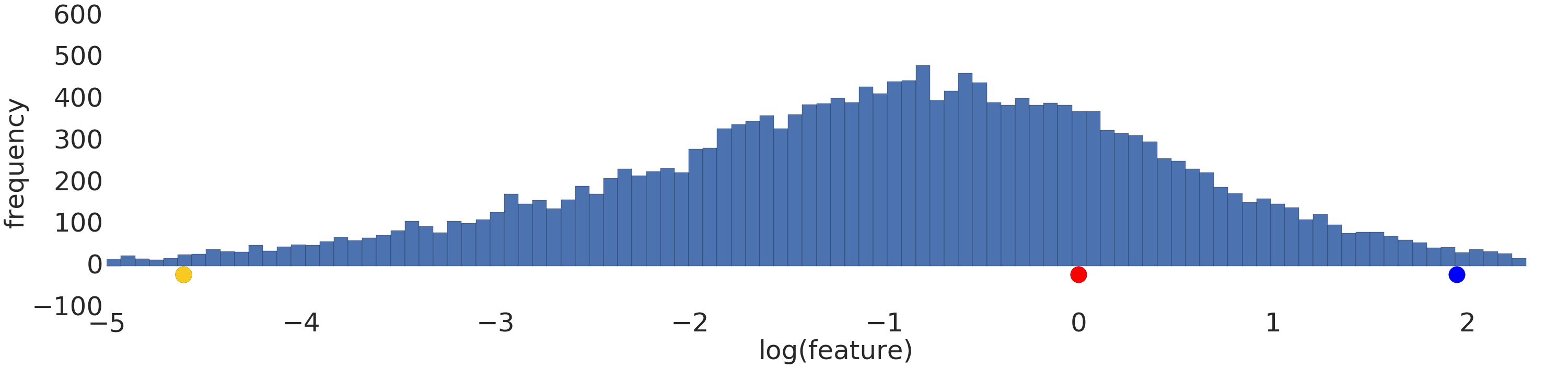
До масштабирования журнала (рис. 2) красный пример больше похож на желтый. После масштабирования журнала (рис. 3) красный цвет становится более похожим на синий.
Квантили
Объединение данных в квантили хорошо работает, когда набор данных не соответствует известному распределению. Возьмем, к примеру, этот набор данных:

Интуитивно понятно, что два примера более похожи, если между ними находится всего несколько примеров, независимо от их значений, и более несходны, если между ними находится много примеров. Визуализация выше затрудняет представление общего количества примеров, попадающих между красным и желтым или между красным и синим.
Это понимание сходства может быть достигнуто путем разделения набора данных на квантили или интервалы, каждый из которых содержит равное количество примеров, и присвоения индекса квантиля каждому примеру. См. раздел «Квантильное группирование» , чтобы просмотреть шаги.
Вот предыдущее распределение, разделенное на квантили, показывающее, что красный цвет отстоит на один квантиль от желтого и на три квантиля от синего:
![График, показывающий данные после преобразования на квантили. Линия представляет 20 интервалов.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=00&hl=ru)
Вы можете выбрать любое число \(n\) квантилей. Однако для того, чтобы квантили осмысленно представляли базовые данные, ваш набор данных должен иметь как минимум\(10n\) примеры. Если у вас недостаточно данных, вместо этого выполните нормализацию.
Проверьте свое понимание
При ответе на следующие вопросы предположите, что у вас достаточно данных для создания квантилей.
Вопрос первый
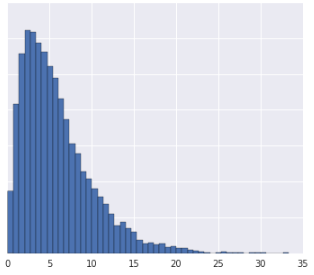
- Распределение данных является гауссовым.
- У вас есть некоторое представление о том, что представляют собой данные в реальности, что позволяет предположить, что данные не следует преобразовывать нелинейно.
Вопрос второй
Отсутствующие данные
Если в вашем наборе данных есть примеры с отсутствующими значениями для определенного объекта, но эти примеры встречаются редко, вы можете удалить эти примеры. Если эти примеры встречаются часто, вы можете либо вообще удалить эту функцию, либо спрогнозировать недостающие значения из других примеров, используя модель машинного обучения. Например, вы можете вменить недостающие числовые данные , используя модель регрессии, обученную на существующих данных объектов.
