Биннинг (также называемый группировкой ) — это метод проектирования функций , который группирует различные числовые поддиапазоны в интервалы или сегменты . Во многих случаях биннинг превращает числовые данные в категориальные данные. Например, рассмотрим объект с именем X , наименьшее значение которого равно 15, а максимальное значение — 425. Используя группирование, вы можете представить X с помощью следующих пяти интервалов:
- Ячейка 1: от 15 до 34
- Ячейка 2: от 35 до 117
- Ячейка 3: от 118 до 279
- Ячейка 4: от 280 до 392
- Ячейка 5: с 393 по 425
Ячейка 1 охватывает диапазон от 15 до 34, поэтому каждое значение X от 15 до 34 попадает в ячейку 1. Модель, обученная на этих ячейках, не будет реагировать по-разному на значения X 17 и 29, поскольку оба значения находятся в ячейке 1.
Вектор признаков представляет пять интервалов следующим образом:
| Номер ячейки | Диапазон | Вектор признаков |
|---|---|---|
| 1 | 15-34 | [1,0, 0,0, 0,0, 0,0, 0,0] |
| 2 | 35-117 | [0,0, 1,0, 0,0, 0,0, 0,0] |
| 3 | 118-279 | [0,0, 0,0, 1,0, 0,0, 0,0] |
| 4 | 280-392 | [0,0, 0,0, 0,0, 1,0, 0,0] |
| 5 | 393-425 | [0,0, 0,0, 0,0, 0,0, 1,0] |
Несмотря на то, что X представляет собой один столбец в наборе данных, группирование заставляет модель рассматривать X как пять отдельных объектов. Таким образом, модель изучает отдельные веса для каждой корзины.
Биннинг является хорошей альтернативой масштабированию или обрезке при выполнении любого из следующих условий:
- Общая линейная связь между признаком и меткой слабая или отсутствует.
- Когда значения признаков кластеризованы.
Биннинг может показаться нелогичным, учитывая, что модель в предыдущем примере обрабатывает значения 37 и 115 одинаково. Но когда объект выглядит более комковатым, чем линейным, бинирование — гораздо лучший способ представления данных.
Пример группировки: количество покупателей в зависимости от температуры
Предположим, вы создаете модель, которая прогнозирует количество покупателей по наружной температуре в этот день. Вот график зависимости температуры от количества покупателей:
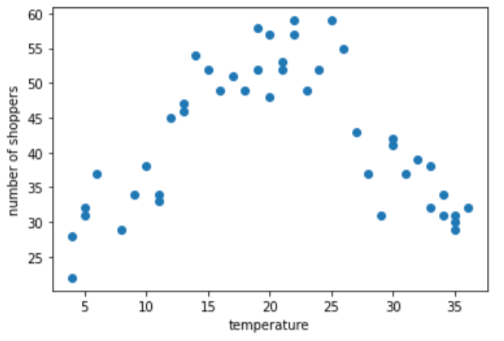
Неудивительно, что график показывает, что количество покупателей было самым высоким тогда, когда температура была наиболее комфортной.
Вы можете представить объект в виде необработанных значений: температура 35,0 в наборе данных будет равна 35,0 в векторе объектов. Это лучшая идея?
Во время обучения модель линейной регрессии изучает один вес для каждой функции. Следовательно, если температура представлена как один признак, то температура 35,0 будет иметь в пять раз большее влияние (или одну пятую) в прогнозе, чем температура 7,0. Однако график на самом деле не показывает какой-либо линейной зависимости между меткой и значением признака.
На графике представлены три кластера в следующих поддиапазонах:
- Ячейка 1 — это диапазон температур 4–11.
- Ячейка 2 – это диапазон температур 12-26.
- Ячейка 3 – диапазон температур 27-36.

Модель запоминает отдельные веса для каждой корзины.
Хотя можно создать более трех интервалов, даже отдельный интервал для каждого показания температуры, часто это плохая идея по следующим причинам:
- Модель может изучить связь между корзиной и этикеткой только в том случае, если в этой корзине достаточно примеров. В данном примере каждая из трех корзин содержит не менее 10 примеров, чего может быть достаточно для обучения. При наличии 33 отдельных ячеек ни одна из ячеек не будет содержать достаточно примеров для обучения модели.
- Отдельный контейнер для каждой температуры дает 33 отдельные температурные характеристики. Однако обычно следует минимизировать количество элементов в модели.
Упражнение: Проверьте свое понимание.
На следующем графике показана средняя цена дома на каждые 0,2 градуса широты в мифической стране Фридония:
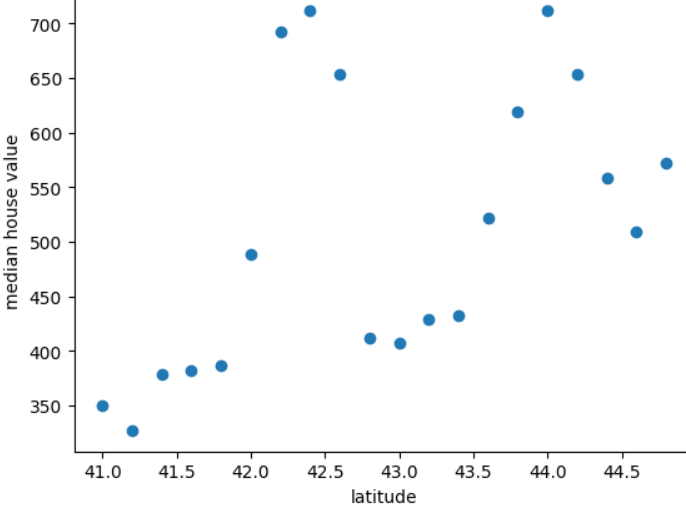
На рисунке показана нелинейная закономерность между значением дома и широтой, поэтому представление широты в виде значения с плавающей запятой вряд ли поможет модели сделать хорошие прогнозы. Возможно, лучше было бы объединить широты?
- от 41,0 до 41,8
- от 42,0 до 42,6
- от 42,8 до 43,4
- от 43,6 до 44,8
Квантильное группирование
Квантильное группирование создает границы группирования таким образом, чтобы количество примеров в каждом сегменте было точно или почти одинаково. Квантильное группирование в основном скрывает выбросы.
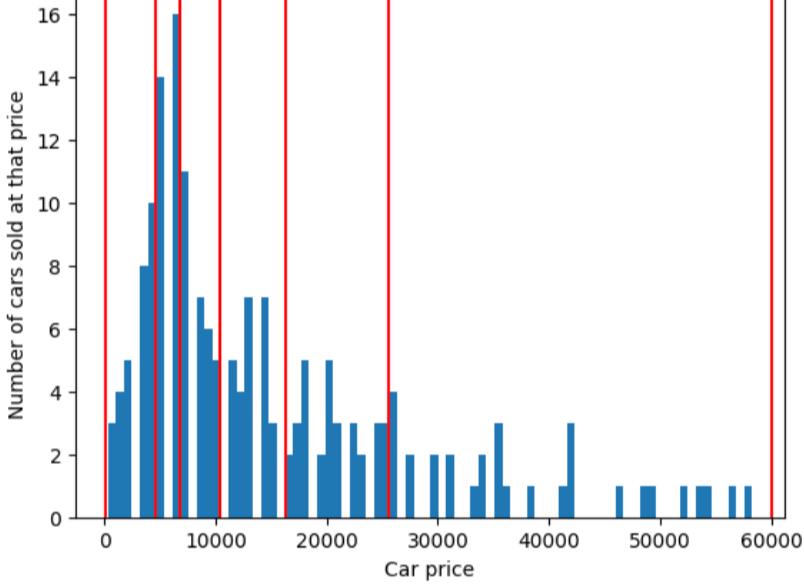
Чтобы проиллюстрировать проблему, которую решает квантильное группирование, рассмотрим равноотстоящие друг от друга сегменты, показанные на следующем рисунке, где каждый из десяти сегментов представляет интервал ровно в 10 000 долларов. Обратите внимание, что сегмент от 0 до 10 000 содержит десятки примеров, а сегмент от 50 000 до 60 000 содержит только 5 примеров. Следовательно, у модели достаточно примеров для обучения в сегменте от 0 до 10 000, но недостаточно примеров для обучения в сегменте от 50 000 до 60 000.
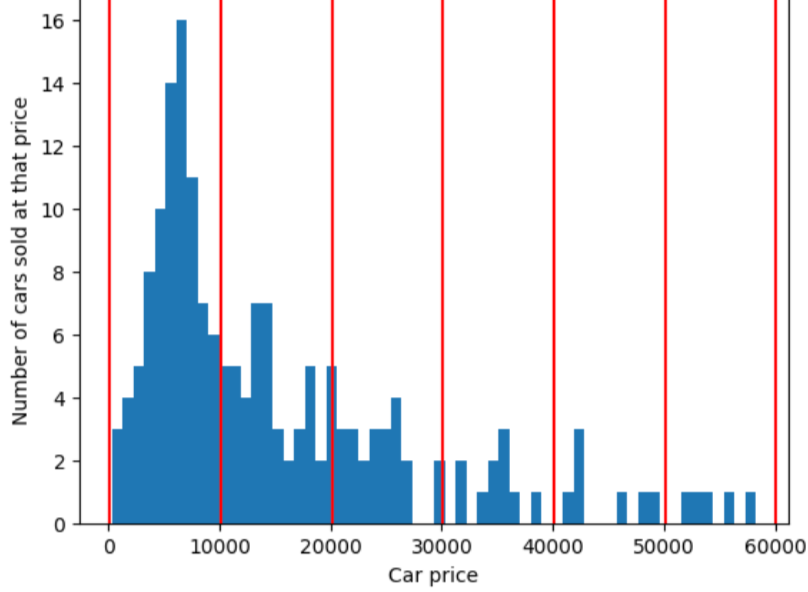
Напротив, на следующем рисунке используется квантильное группирование для разделения цен на автомобили на корзины с примерно одинаковым количеством примеров в каждой корзине. Обратите внимание, что некоторые корзины охватывают узкий ценовой диапазон, тогда как другие охватывают очень широкий ценовой диапазон.