Cette section passe en revue les étapes de préparation des données les plus pertinentes pour le clustering à partir du module Travailler avec des données numériques du cours d'initiation au machine learning.
Dans le clustering, vous calculez la similarité entre deux exemples en combinant toutes les données de caractéristiques de ces exemples en une valeur numérique. Pour ce faire, les caractéristiques doivent avoir la même échelle, ce qui peut être obtenu en les normalisant, en les transformant ou en créant des quantiles. Si vous souhaitez transformer vos données sans examiner leur distribution, vous pouvez utiliser les quantiles par défaut.
Normaliser les données
Vous pouvez transformer les données de plusieurs éléments à la même échelle en les normalisant.
Scores Z
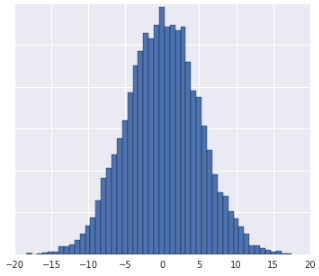
Chaque fois que vous voyez un ensemble de données ayant à peu près la forme d'une distribution gaussienne, vous devez calculer les scores z pour les données. Les scores Z correspondent au nombre d'écarts types d'une valeur par rapport à la moyenne. Vous pouvez également utiliser des scores Z lorsque l'ensemble de données n'est pas assez volumineux pour les quantiles.
Consultez la section Échelle de score Z pour connaître la procédure.
Voici une visualisation de deux caractéristiques d'un ensemble de données avant et après la mise à l'échelle du score z:
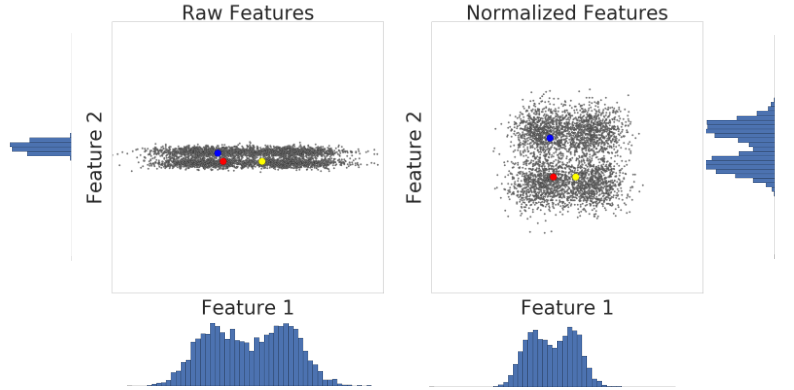
Dans l'ensemble de données non normalisé de gauche, les caractéristiques 1 et 2, représentées respectivement sur les axes X et Y, n'ont pas la même échelle. À gauche, l'exemple rouge semble plus proche, ou plus semblable, du bleu que du jaune. À droite, après la mise à l'échelle de la note z, les caractéristiques 1 et 2 ont la même échelle, et l'exemple rouge semble plus proche de l'exemple jaune. L'ensemble de données normalisé fournit une mesure plus précise de la similarité entre les points.
Transformations de journaux
Lorsqu'un ensemble de données se conforme parfaitement à une distribution de loi de puissance, où les données sont fortement regroupées aux valeurs les plus basses, utilisez une transformation logarithmique. Consultez la section Échelle des journaux pour connaître la procédure à suivre.
Voici une visualisation d'un ensemble de données de loi de puissance avant et après une transformation logarithmique:
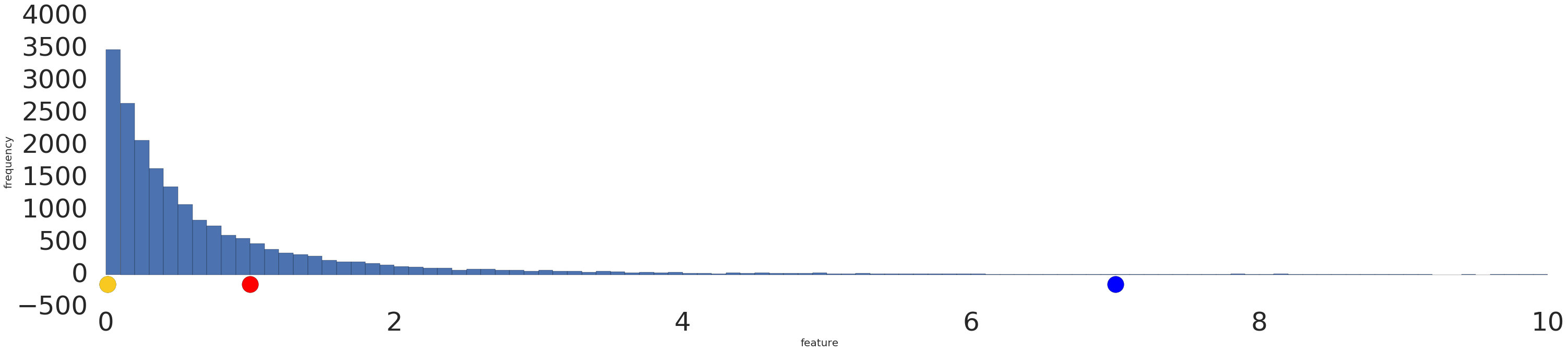
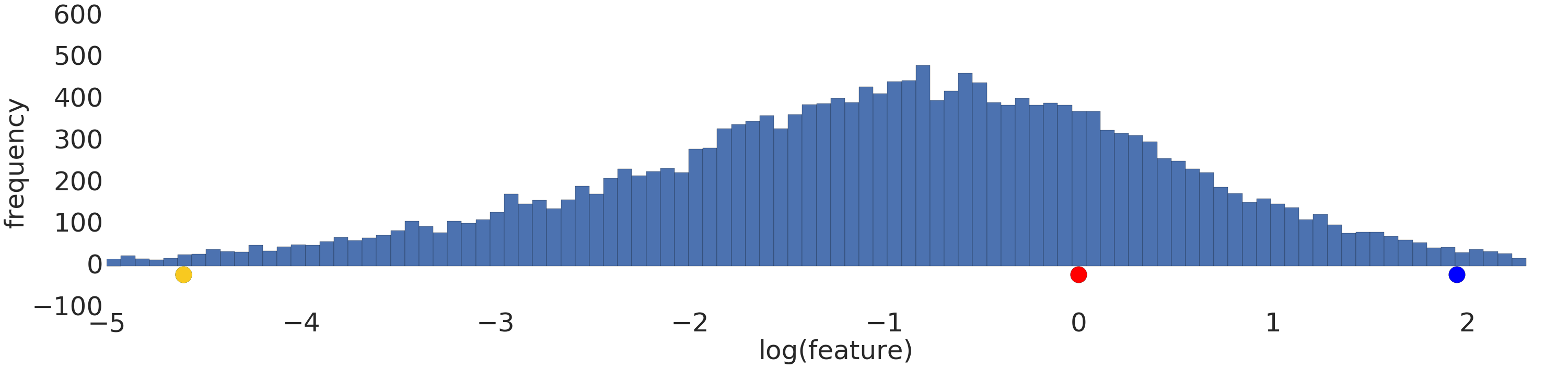
Avant la mise à l'échelle de la journalisation (figure 2), l'exemple rouge ressemble plus au jaune. Après la mise à l'échelle des journaux (figure 3), le rouge ressemble davantage au bleu.
Quantiles
La répartition des données en quantiles fonctionne bien lorsque l'ensemble de données ne se conforme pas à une distribution connue. Prenons cet ensemble de données, par exemple:

Intuitif, deux exemples sont plus similaires si seuls quelques exemples se situent entre eux, indépendamment de leurs valeurs, et plus dissemblables si de nombreux exemples se situent entre eux. La visualisation ci-dessus rend difficile la visualisation du nombre total d'exemples situés entre le rouge et le jaune, ou entre le rouge et le bleu.
Cette compréhension de la similarité peut être mise en évidence en divisant l'ensemble de données en quantiles, ou intervalles contenant chacun un nombre égal d'exemples, et en attribuant l'indice de quantile à chaque exemple. Consultez la section Batiement par quantile pour connaître la procédure.
Voici la distribution précédente divisée en quantiles, montrant que le rouge est à un quantile du jaune et à trois quantiles du bleu:
![Graphique montrant les données après conversion en quantiles. La ligne représente 20 intervalles.]](https://developers.google.cn/static/machine-learning/clustering/images/Quantize.png?authuser=6&hl=fr)
Vous pouvez choisir n'importe quel nombre \(n\) de quantiles. Toutefois, pour que les quantiles représentent de manière significative les données sous-jacentes, votre ensemble de données doit comporter au moins\(10n\) exemples. Si vous ne disposez pas de suffisamment de données, normalisez-les à la place.
Vérifier vos connaissances
Pour les questions suivantes, partez du principe que vous disposez de suffisamment de données pour créer des quantiles.
Première question
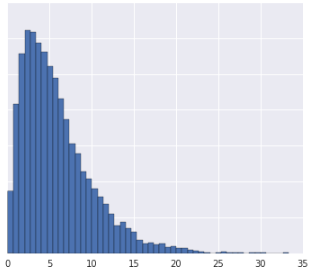
- La distribution des données est gaussienne.
- Vous avez un aperçu de ce que les données représentent dans le monde réel, ce qui suggère qu'elles ne doivent pas être transformées de manière non linéaire.
Deuxième question
Données manquantes
Si votre ensemble de données contient des exemples avec des valeurs manquantes pour une caractéristique donnée, mais que ces exemples sont rares, vous pouvez les supprimer. Si ces exemples se produisent fréquemment, vous pouvez soit supprimer complètement cette fonctionnalité, soit prédire les valeurs manquantes à partir d'autres exemples à l'aide d'un modèle de machine learning. Par exemple, vous pouvez imputer des données numériques manquantes à l'aide d'un modèle de régression entraîné sur des données de fonctionnalités existantes.