Im Allgemeinen wirken sich Media verzögert auf Leistungskennzahlen (key performance indicators, KPIs) aus und der Effekt nimmt mit der Zeit ab. Um diesen verzögerten Effekt zu modellieren, transformieren wir die Media-Ausführung eines bestimmten Channels mit der Adstock-Funktion:
Dabei gilt:
\(w(s; \alpha) \) ist eine nicht negative Gewichtungsfunktion.
\(x_s \geq 0\) ist die Media-Ausführung zum Zeitpunkt \(s\).
\(\alpha\ \in\ [0, 1]\) ist der Abklingparameter.
\(L\) ist die maximale Verzögerungsdauer.
In Meridian gibt es zwei Abklingkurven: geometrisch und binomisch. Die Geschwindigkeit, mit der der Media-Effekt abnimmt, wird durch die Auswahl der Funktion und den gelernten Parameter Alpha bestimmt. Mit dem Parameter adstock_decay_spec der ModelSpec wird festgelegt, welche Funktion oder Kombination von Funktionen verwendet wird.
Wenn Sie beispielsweise das binomische Abklingen für alle Channels nutzen möchten, können Sie Folgendes verwenden:
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec='binomial'
)
Gehen Sie so vor, um für die drei Channels "Channel0", "Channel1" und "Channel2" jeweils den binomischen, geometrischen und binomischen Mechanismus zu verwenden:
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec=dict(
Channel0='binomial',
Channel1='geometric',
Channel2='binomial',
)
)
Im Allgemeinen empfehlen wir den binomischen Ansatz, wenn davon auszugehen ist, dass ein erheblicher Teil der verzögerten Effekte eines Media-Channels auch in der zweiten Hälfte des Wirkungszeitraums anhält. Andernfalls empfehlen wir die Verwendung des geometrischen Abklingens.
Mit diesen Funktionen werden Gewichtungen \(w(s; \alpha)\) für die Adstock-Funktion definiert. Sie werden so definiert, dass zum Zeitpunkt \(t-s\) die Media-Ausführung zum Zeitpunkt \(t\)die Gewichtung \(w(s; \alpha) / \sum_{s\in{\{0, ..., L\}}}w(s; \alpha)\)hat. Weitere Informationen zur Adstock-Funktion finden Sie unter Media – Übersättigung und Verzögerung.
Geometrisches Abklingen
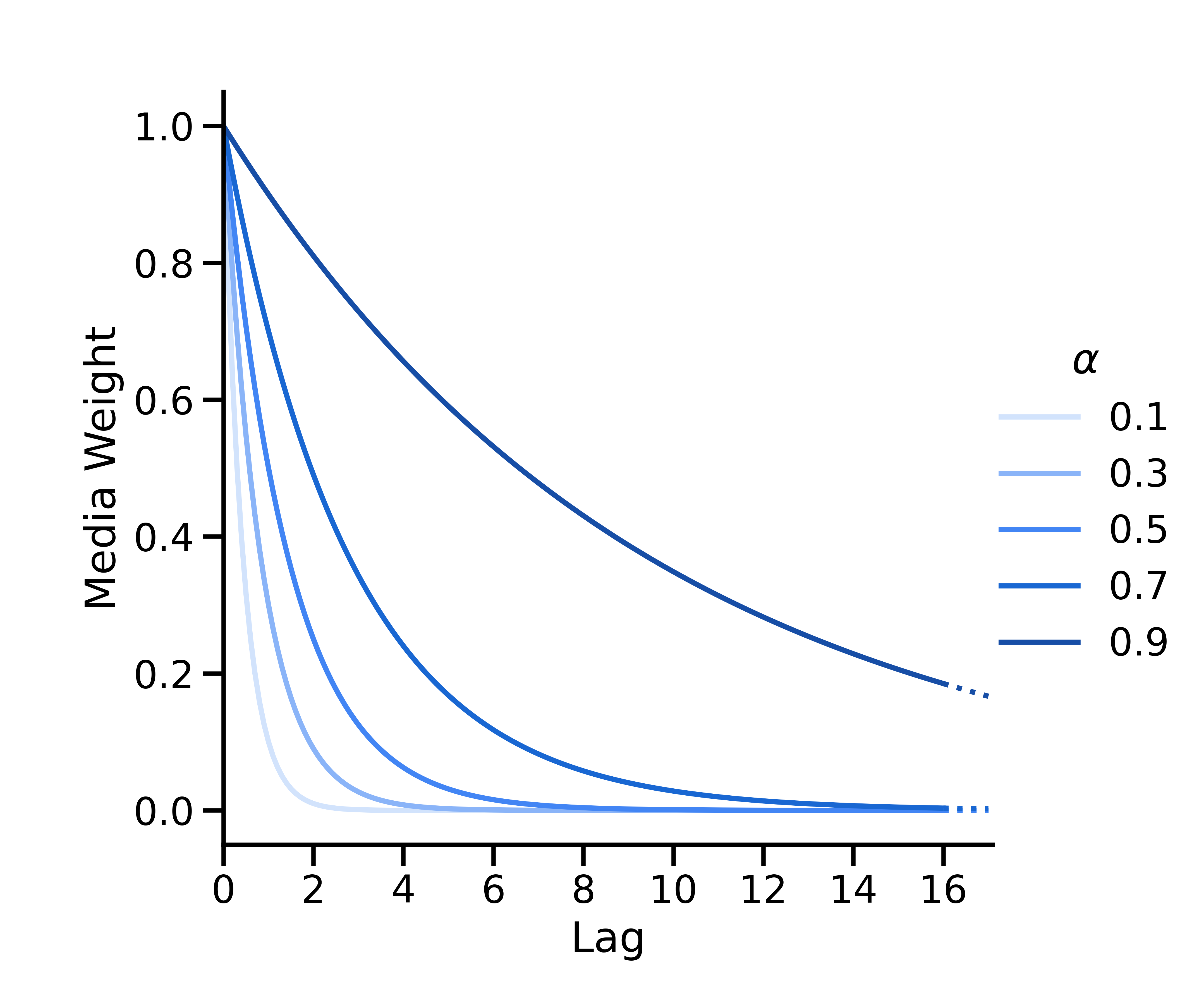
Das geometrische Abklingen wird durch \(w(s; \alpha) = \alpha^s\)parametrisiert, wobei\(\alpha \in [0, 1] \) der geometrische Parameter für die Abklingrate und\(s\) die Verzögerung ist. Zum Zeitpunkt \(t\)hat die Media-Ausführung zum Zeitpunkt \(t-s\) die Gewichtung \(w(s; \alpha) = \alpha^s\), die dann so normalisiert wird, dass alle Gewichtungen zusammen eins ergeben.
Binomisches Abklingen
Das binomische Abklingen wird so parametrisiert:
Dabei ist \(L\) die maximale Verzögerung (der Parameter max_lag der ModelSpec). Die Abbildung \(\alpha_*=\frac{1}{\alpha} - 1\) wird verwendet, um Werte von\(\alpha\) aus dem Bereich \([0, 1]\) auf den Bereich \([0, \infty)\)abzubilden.
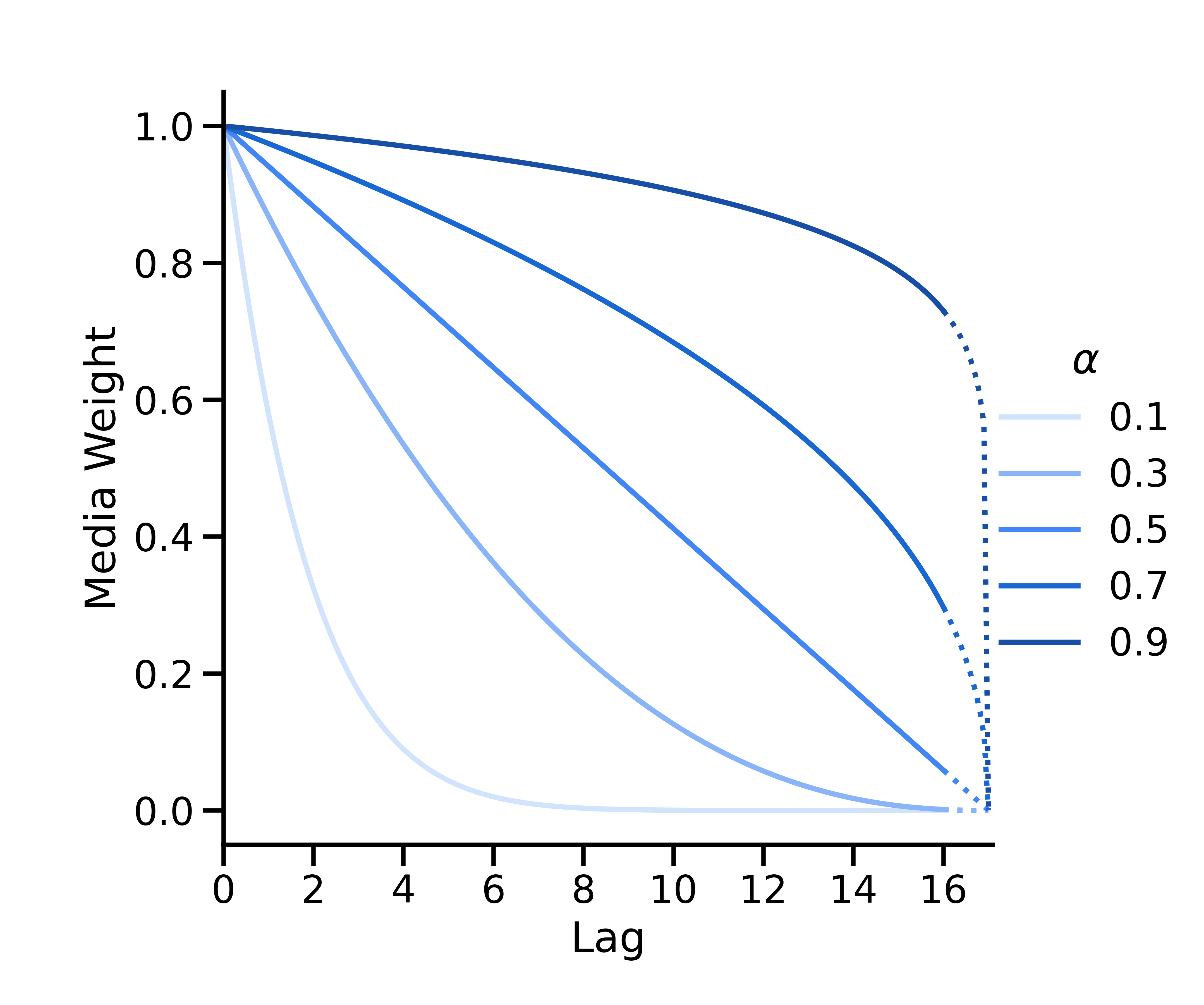
Die binomische Kurve ist konvex, wenn \(\alpha < 0.5\), linear, wenn \(\alpha = 0.5\), und konkav, wenn \(\alpha > 0.5\). Sie ist so definiert, dass ihr Schnittpunkt mit der x-Achse immer bei \(L + 1\)liegt.
Zwischen geometrischem und binomischem Abklingen entscheiden
Wir empfehlen, den binomischen Abklingeffekt auszuwählen, wenn Sie der Meinung sind, dass ein Channel in der zweiten Hälfte des Wirkungszeitraums einen erheblichen Anteil seiner Effekte entfaltet. Andernfalls wählen Sie das geometrische Abklingen aus.
Die Abklingkurve wirkt sich auf die relativen Gewichtungen verzögerter Media aus. Wenn Sie die relative Gewichtung späterer Zeiträume erhöhen, verringert sich zwangsläufig die relative Gewichtung früherer Zeiträume. Die binomische Abklingkurve definiert Gewichtungen, die langsamer auf null abfallen als die geometrische Kurve. Bei der binomischen Abklingkurve entfaltet sich ein größerer Teil der gesamten Media-Effekte eines Channels später, bei der geometrischen Kurve eher früher. Die binomische Abklingkurve eignet sich besonders bei großen max_lag-Werten, weil sie das gesamte Wirkungsfenster abdeckt. Ihr Schnittpunkt mit der x-Achse liegt dabei immer bei \(L + 1\). Weitere Informationen finden Sie unter Parameter „max_lag“ festlegen.
Es kann verlockend sein, die binomische Abklingkurve für alle Channels auszuwählen, da sie größere max_lag-Werte unterstützt. Allerdings lassen sich nicht alle Channels bestmöglich mit der binomischen Abklingkurve modellieren. Sie eignet sich besonders gut, wenn Sie davon ausgehen, dass ein Channel einen erheblichen Teil seiner Effekte in der zweiten Hälfte des Wirkungszeitraums entfaltet. Die falsche Anwendung der binomischen Abklingkurve kann dazu führen, dass kurzfristige Effekte unterschätzt werden.
| Funktion | Geometrisch | Binomisch |
|---|---|---|
| Optimal für | Media mit kurzlebigen Effekten | Media mit Effekten, die bis in die zweite Hälfte des Wirkungszeitraums anhalten |
| Kurvenform | Schnelles Abklingen | Können länger anhalten, bevor sie abklingen |
| Empfehlung für maximale Verzögerung | 2 bis 10 Zeiträume | 4 bis 20 Zeiträume |
| Nachteile | Anfällig für eine Unterschätzung der langfristigen Effekte | Anfällig für eine Unterschätzung der kurzfristigen Effekte |
Hinweise zu langfristigen Effekten
Wenn Sie langfristige Effekte erwarten, die in einem Modell nicht sichtbar werden, kann eine Kombination aus binomischer Abklingkurve, Anpassung des Priors für Alpha und Änderung von max_lag helfen. Nutzen Sie die Prior-Kurven aus MediaEffects.plot_adstock_decay, um zu sehen, wie max_lag, der Alpha-Prior und die Abklingfunktion interagieren. Anschließend können Sie diese Parameter feinabstimmen, um ein Modell an Ihre ursprünglichen Annahmen zu verzögerten Effekten anzupassen. Die Anpassung des Priors und von max_lag kann parallel zur oder anstelle der Auswahl einer bestimmten Abklingfunktion erfolgen. Wir empfehlen, mit verschiedenen Kombinationen zu experimentieren, um Konvergenz, Modellanpassung und Wirkungszeitraum in Einklang zu bringen. Weitere Informationen zur Auswahl eines Werts für max_lag finden Sie unter Parameter „max_lag“ festlegen.
Der Alpha-Prior
Der Standard-Alpha-Prior in Meridian ist \(U(0, 1)\). Das ist ein nicht informativer Prior für geometrische und binomische Abklingfunktionen. Wenn Sie eine Vermutung dazu haben, wie schnell der Media-Effekt für einen bestimmten Channel nachlässt, können Sie einen benutzerdefinierten Alpha-Prior dafür festlegen, um Meridian entsprechend zu informieren.
Sowohl beim geometrischen als auch binomischen Abklingen besteht eine monotone Beziehung zwischen\(\alpha\) und der Rate, mit der der Media-Effekt abklingt: Ein kleinerer \(\alpha\)entspricht einem schnelleren, ein größerer \(\alpha\) einem langsameren Abklingen. Sowohl geometrische als auch binomische Funktionen maximieren kurzfristige Effekte, wenn \(\alpha=0\). In diesem Fall gibt es keine verzögerten Effekte. Langfristige Effekte werden maximiert, wenn \(\alpha=1\). In diesem Fall werden alle Media innerhalb des historischen verzögerten Zeitraums gleich gewichtet.
Daher empfehlen wir, einen Prior für Alpha festzulegen, bei dem mehr Gewicht nahe null liegt, um ein schnelleres Abklingen und kurzfristige Effekte zu fördern. Eine Beta(1, 3)-Verteilung hat beispielsweise mehr Gewicht nahe null als die standardmäßige einheitliche Verteilung. Umgekehrt empfehlen wir, einen Prior mit mehr Gewicht nahe eins festzulegen, um ein langsameres Abklingen und langfristige Effekte zu erzielen. Eine Beta(3, 1)-Verteilung hat beispielsweise mehr Gewicht nahe eins als die standardmäßige einheitliche Verteilung. Sie sollten die Prior-Verteilungen von Alpha und Media-Gewichten (mit MediaEffects.plot_adstock_decay) darstellen, um sicherzustellen, dass die benutzerdefinierten Prior-Verteilungen Ihren Erwartungen entsprechen.
Die binomische \(\alpha\) -Abbildung
Die Abbildung \(\alpha_*: [0, 1]\rightarrow[0, \infty) \) wird durchgeführt, weil die binomische Funktion für \(\alpha_* \in [0, \infty)\) abklingt, während die geometrische Funktion für \(\alpha \in [0, 1]\)abklingt. Durch diese Abbildung können Priors, die im Intervall \([0, 1]\) definiert sind, im binomischen Fall korrekt auf \([0, \infty)\) übertragen werden. Außerdem wird dafür gesorgt, dass die Modellspezifikation mit der geometrischen Abklingfunktion konsistent bleibt. Niedrige Alpha-Werte implizieren ein schnelles Abklingen und kurzfristige Effekte, höhere Werte ein langsames Abklingen und langfristige Effekte.
Erweiterte Option: Benutzerdefinierten Prior direkt auf \(\alpha_*\) setzen, wenn die binomische Abklingfunktion verwendet wird
Meridian verwendet standardmäßig einen Prior \(U(0, 1)\) auf \(\alpha\) für geometrische und binomische Funktionen. Bei binomischem Abklingen entspricht ein Prior \(U(0, 1)\) auf\(\alpha\) einem Lomax(1, 1)-Prior auf \(\alpha_*\):

Der Prior ist eher uninformativ, damit die Daten selbst zeigen, wie schnell die Wirkung bei binomischer Abklingung abnimmt.
Meridian geht davon aus, dass benutzerdefinierte \(\alpha\) -Priors im Bereich \([0, 1]\) liegen (z. B. Beta-Verteilung) und dann mit \(1/x-1\)auf die nicht negativen reellen Zahlen abgebildet werden. Wenn Sie jedoch einen Prior auf \(\alpha_*\) im Bereich \([0, \infty)\) definieren möchten, können Sie ihn anschließend mit der inversen Abbildung \(\frac{1}{1+x}\)transformieren. Dafür ist die Hilfsmethode adstock_hill.transform_non_negative_reals_distribution verfügbar.
Wenn Sie beispielsweise einen lognormalen Prior auf \(\alpha_*\) mit Mittelwert 0,5 und Varianz 0,5 erhalten möchten, gehen Sie so vor:
import tensorflow as tf
# Example: pick mu, sigma so that the mean, variance of alpha_* are both 0.5
mu = -tf.math.log(2.0) - 0.5 * tf.math.log(3.0)
sigma = tf.math.sqrt(tf.math.log(3.0))
alpha_star_prior = tfp.distributions.LogNormal(mu, sigma) # prior on alpha_* for binomial
alpha_prior = adstock_hill.transform_non_negative_reals_distribution(alpha_star_prior)
prior = prior_distribution.PriorDistribution(
alpha_m=alpha_prior
)
model_spec = spec.ModelSpec(
prior=prior,
adstock_decay_spec='binomial'
)
Anschließend können Sie den Alpha-Prior auch direkt untersuchen, z. B. um die Wahrscheinlichkeitsdichtefunktion von Alpha zu betrachten:
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, alpha_prior.prob(x), linewidth=3)
ax.set(xlabel='Alpha', ylabel='Probability')
plt.show()

Dieses Diagramm zeigt den Prior auf \(\alpha\) , der zu einem lognormalen Prior auf\(\alpha_*\) mit einem Mittelwert und einer Varianz von jeweils 0,5 führt.
